交通 | 机器学习 + 大规模TSP/VRP求解

封面图来源：https://xkcd.com/399/

推文作者：丁建辉，陈泰劼，张云天

本文针对旅行商问题（Travelling salesman problem, TSP）和车辆路径规划问题（Vehicle routing problem, VRP）这一类经典而重要的运筹学问题，归纳与探讨基于机器学习技术的新求解方法。本文从“分而治之”、“持续局部优化”、“调整模型结构”和“调整学习范式”四个角度归纳新方法，并欢迎读者评论、讨论与推荐某一角度中的好文章、新文章。

概述：机器学习 + 大规模TSP/VRP求解

TSP/VRP是交通物流行业的经典问题，目前广泛应用于快递、外卖配送等业务场景。对于中小规模TSP/VRP，主流的启发式算法已经解决得比较好，即能在可接受的时间内求得较好的可行解。然而，当问题的规模变得特别大时，现有的启发式算法通常需要比较长的时间才能获得满意的可行解。此外，类似业务所衍生出来的TSP/VRP在目标、约束、数据分布上会比较接近，其可行解也大概率存在相关性。然而，启发式算法无法利用问题间的相关性以及历史求解信息加速问题的求解，即每遇到1个新问题，启发式算法都得从头开始。

考虑到机器学习模型能从大规模数据中挖掘出潜在的规律且在数据分布类似的场景上具有较好的泛化性，不少专家学者尝试将机器学习以及启发式算法结合到一起，并以此加快大规模TSP/VRP问题的求解。从模型整体的优化目标看，目前的ml4tsp方案主要分为2类：端到端的Construction以及局部迭代优化的Improvement。前者通常直接使用机器学习模型构建问题的解，具有速度快、在小规模问题上求解效果好等优点，其缺点是在中大规模问题上的求解效果跟最优解的gap还比较大以及跨数据分布的泛化能力还不尽人如意。后者通常结合了机器学习以及启发式算法，例如将邻域搜索算子选择转化成数据驱动的分类问题。局部迭代优化方案的优点是融合了机器学习和启发式算法的长处，能较好地求解不同规模的优化问题，其缺点是在大规模问题上的求解效率还有待提升。

另外，从模型结构看，现有的ml4tsp方案主要有2种：基于图神经网络以及基于transformer，前者通常将tsp问题转化成图的边分类任务（非自回归），而后者则将tsp问题转化成序列建模任务（自回归）。对于这2种方案，若直接在大规模tsp问题（例如节点数量大于5k）上训练，均会存在效率&资源上的问题。对于图神经网络方案，若以模仿学习的范式进行学习，则需要提前给大规模tsp问题构建较好的可行解（例如使用LKH提前求解），这个阶段会非常耗时。此外，当节点数量等于5k时，tsp问题形成的图包含了1kw+条边，在这种规模的图上进行边分类任务，存在学习难度大且解码环节耗资源的问题。另外，对于基于transformer的序列求解方案，其核心的self-attention的时间复杂度是O(tsp问题节点数量的平方)，当tsp规模特别大时，transformer类方案在训练阶段也存在特别耗时的问题。

从前面的分析可知，使用机器学习模型求解大规模问题很有价值（效率提升）但也存在很大的挑战（泛化性）。为了攻克这个难题，研究人员主要从以下几个角度提出了新的优化方案：

分而治之：先将大问题分解成小问题，然后优化求解；
持续局部优化：先选出值得优化的局部区域，然后继续优化求解；
调整模型结构：泛化性分析、优化编码-解码框架、改进attention；
调整学习范式：降低数据成本；

1. 分而治之：先分解，后求解

[AAAI 2021] Generalize a Small Pre-trained Model to Arbitrarily Large TSP Instances

Fu, Z. H., Qiu, K. B., & Zha, H. (2021, May). Generalize a small pre-trained model to arbitrarily large tsp instances. In Proceedings of the AAAI conference on artificial intelligence (Vol. 35, No. 8, pp. 7474-7482).

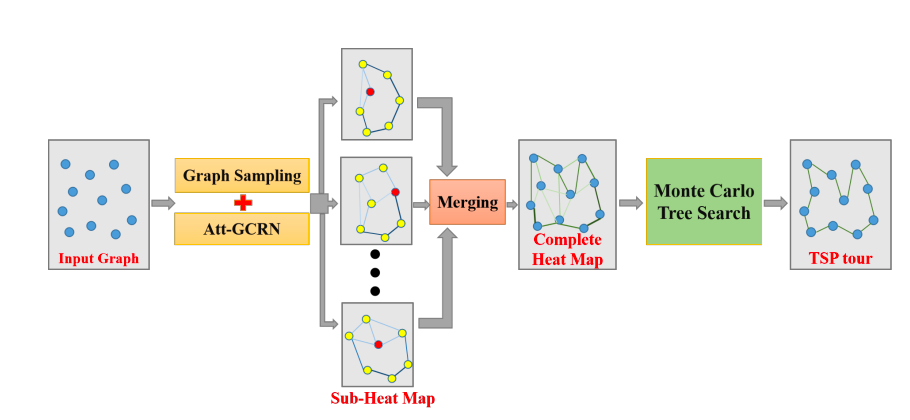
这篇文章提出了包含图神经网络以及蒙特卡洛树搜索的融合方案，其主要包含3个关键模块：

大问题分解：将tsp问题抽象成graph，然后使用抽样策略将原始graph拆解成多个subgraph（均包含k个节点）；
小问题求解：将tsp问题的求解转化成graph上的边分类问题（边的得分越高，说明其属于最优路线的概率越大），并使用模仿学习范式训练了1个图神经网络。完成训练后，统一使用这个图神经网络计算tsp subgraph上不同边的得分；
持续优化：将前面拆解出来的tsp subgraph合并形成完整的tsp graph。然后在这个graph上使用强化学习 & 蒙特卡洛树搜索持续优化可行解；

「运筹OR帷幄」社区也曾深度解读过本篇论文，推文链接为：

OM | 机器学习算法求解更大规模的旅行商问题

[ICLR 2023] Generalize Learned Heuristics to Solve Large-scale Vehicle Routing Problems in Real-time

Hou, Q., Yang, J., Su, Y., Wang, X., & Deng, Y. (2022, September). Generalize learned heuristics to solve large-scale vehicle routing problems in real-time. In The Eleventh International Conference on Learning Representations.

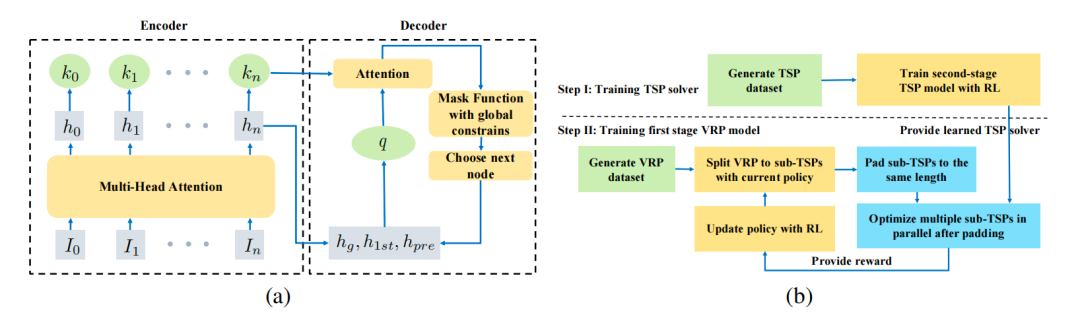
这篇文章同样提出了1个分而治之方案 Two-stage Divide Method（TAM），其亮点是在保障可行解质量的前提下实时地求解大规模cvrp问题，主要包含以下几个关键模块：

大问题分解：设计了1个编码器-解码器框架（使用强化学习范式进行优化），其主要用于将cvrp拆解成多个tsp（同时起到降低问题规模以及求解难度的作用）。为了后续能充分利用GPU资源进行并行求解，还专门将不同子问题padding成相同的规模。此外，为了增强问题分解模块的能力，小问题求解模块会将获得的可行解的质量作为reward反馈给问题分解模块，即2个模块具有较好的协同性；
小问题求解：使用强化学习范式训练1个专门求解小规模tsp的机器学习模型。由于padding后的子问题具备相同的规模，可利用GPU进行快速的并行求解；
全局约束满足：cvrp存在最大车辆数限制以及车辆装载容量上限，TAM巧妙地将这些约束融合到解码逻辑中；

[AAAI 2023] H-tsp: Hierarchically solving the large-scale traveling salesman problem

Pan, X., Jin, Y., Ding, Y., Feng, M., Zhao, L., Song, L., & Bian, J. (2023, June). H-tsp: Hierarchically solving the large-scale traveling salesman problem. In Proceedings of the AAAI Conference on Artificial Intelligence (Vol. 37, No. 8, pp. 9345-9353).

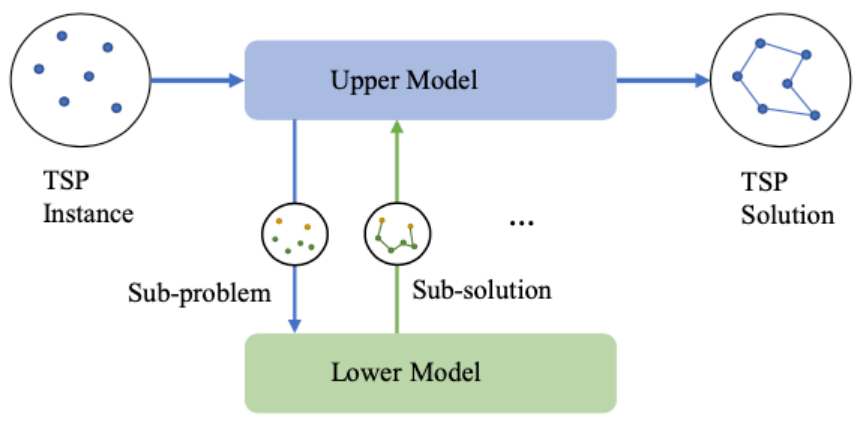
这篇文章提出了端到端的tsp求解方案H-TSP（借鉴了分层强化学习的思路），其主要包含以下几个关键模块：

子问题构建：与前面2篇文章不同，H-TSP没有直接拆解大规模问题，而是结合强化学习算法以及贪心策略依次在还没有访问的节点中选出部分节点并将它们形成1个新的子问题（open-loop tsp）；
子问题求解：前1个模块构建的子问题属于open-loop tsp，即不要求返回起点的tsp。针对这类问题，H-TSP专门设计了另外1个强化学习模型进行求解。完成求解后，会将相关信息合并到现有的部分可行解中；
模块间协同：为了提高最终可行解的质量，H-TSP特意增强了子问题构建&求解模块之间的协同，即同时训练2个模块。此外，为了提高协同训练的稳定性，针对子问题求解模型提前做了热启动训练（后续实验表明这个操作非常关键）；

「运筹OR帷幄」社区也曾深度解读过本篇论文，推文链接为：

交通 | 求解大规模旅行商问题的分层强化学习方法

[AAAI 2024] GLOP: Learning Global Partition and Local Construction for Solving Large-scale Routing Problems in Real-time

Ye, H., Wang, J., Liang, H., Cao, Z., Li, Y., & Li, F. (2024, March). Glop: Learning global partition and local construction for solving large-scale routing problems in real-time. In Proceedings of the AAAI Conference on Artificial Intelligence (Vol. 38, No. 18, pp. 20284-20292).

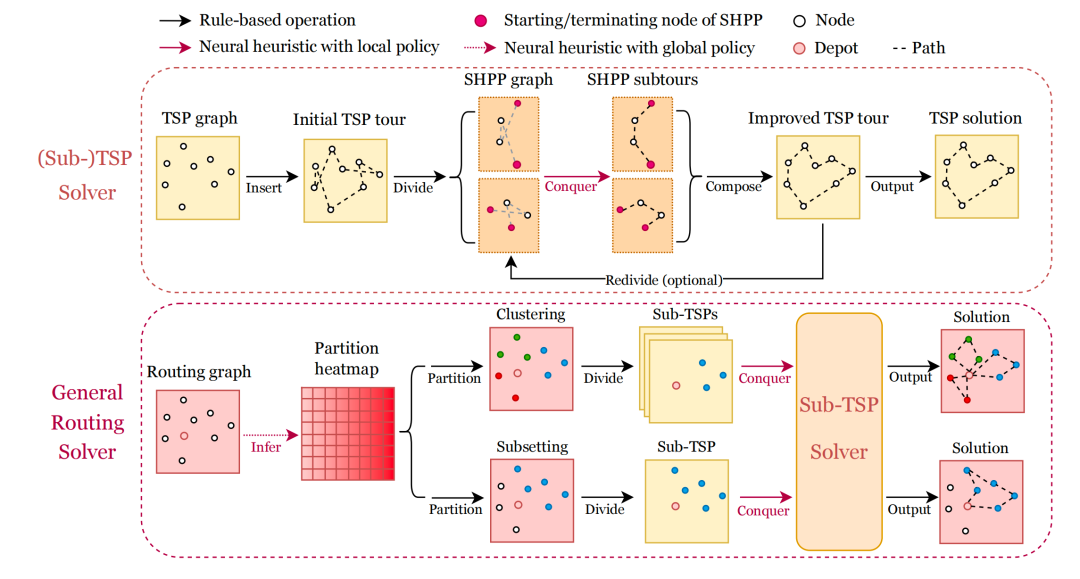
这篇文章介绍了一种名为GLOP（Global and Local Optimization Policies）的大规模TSP/VRP问题求解方案，主要包含以下几个关键模块：

子问题构建：在使用GNN（图神经网络）完成Routing graph的热力图构建后，GLOP会在多个环节对子问题进行多样化的分解：
1. stage1_partition：在这个阶段，主要基于热力图对原始Routing graph中的节点进行分组。目前支持2种模式，直接聚类（clustering）以及特定子集驱动法（subsetting）；
2. stage2_divide：基于stage1_partition的分组结果将节点拆分到不同的sub-tsps中；
3. stage3_divide：先基于Insert启发式算法快速构建不同sub-tsps的初始可行解，然后将sub-tsp拆解成不同的SHPP graph（本质是open-loop tsp，即不需要回到起点的tsp问题）；
子问题求解：
1. 将open-loop tsp转化成序列建模问题，并沿用了经典的AM模型（encoder-decoder框架）。其中，encoder主要负责对open-loop tsp graph进行抽象编码，而decoder则会根据全局约束以及得分分布依次解码出下1个要访问的节点；

2. 持续局部优化：先选局部区域，后优化

[NIPS 2021] Learning to Delegate for Large-scale Vehicle Routing

Li, S., Yan, Z., & Wu, C. (2021). Learning to delegate for large-scale vehicle routing. Advances in Neural Information Processing Systems, 34, 26198-26211.

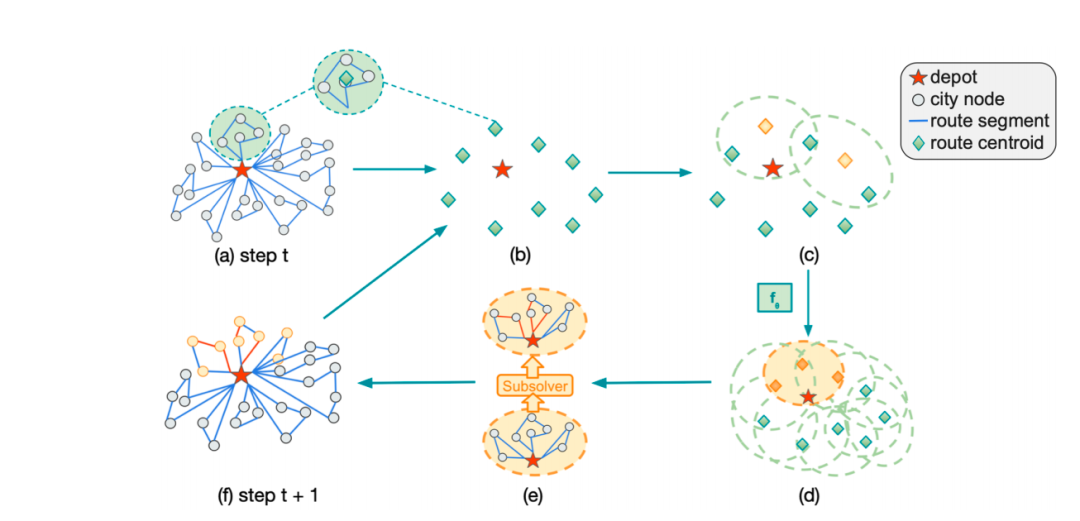
这篇文章提出了针对大规模vrp问题的局部优化求解方案L2D，其主要包含如下几个模块：

初始可行解构建：使用启发式算法快速构建初始可行解；
选择值得优化的子问题：若原始问题的网点数量为N，那么可以形成的子问题总数是2的N次方。为了降低搜索空间，L2D首先对原始问题的不同网点进行聚类分析，从而将大规模问题拆解成多个子问题。接着，使用基于transformer的回归模型对不同子问题的求解价值进行预估。最终，选择得分最高的子问题作为后续的优化对象；
子问题求解：使用启发式算法 or 模型对子问题进行优化求解；
可行解调整：完成子问题的求解后，若子问题的cost有所降低，那么将当前最优可行解对应区域的路线替换成新求解出来的路线；

[AISTATS 2023] Select and Optimize: Learning to solve large-scale TSP instances

Cheng, H., Zheng, H., Cong, Y., Jiang, W., & Pu, S. (2023, April). Select and optimize: Learning to aolve large-scale tsp instances. In International Conference on Artificial Intelligence and Statistics (pp. 1219-1231). PMLR.

这篇文章提出了针对大规模tsp问题的局部优化求解方案，其主要包含如下几个模块：

初始可行解构建：结合K-means聚类分析以及LK算法构建TSP问题的初始解；
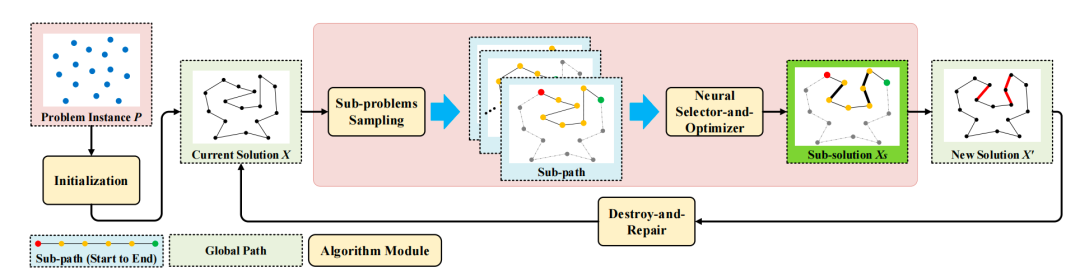
选择值得优化的子问题：包含子图抽样以及Neural Select-and-Optimizer 2个子模块。其中，前者负责从当前最优可行解（tsp solution graph）中采样出很多条sub-paths。为了提高效率，这篇文章设计了1个按照节点序号依次采样的策略，若采用并行运算机制，整体的时间复杂度可以降到O(1)。此外，Neural Select-and-Optimizer模块是1个遵循encoder-decoder框架的模型，其主要负责给前面采样出来的sub graphs（本质是open-loop tsp子问题）构建新的可行解。不同子问题的价值最终由求解前后路线长度的减小程度所决定；
可行解调整：包含路线整合以及破坏重建2个子模块。对于路线整合，主要作用是将Neural Select-and-Optimizer模块产出的收益最大的sub solution融合到先前的最优解中。考虑到这本质是1种单步决策，即只通过当前步而非未来的收益去决定不同决策的优劣，比较容易陷入局部较优解。为了持续提升解的质量，这篇文章还设计了1个 [破坏-重建]子模块，即先移除当前最优solution中longest connections边以及部分其他边（目的是让不同子问题的规模尽可能接近），接着基于Lin–Kernighan算法重新构建1个完整的可行解；

[ICAPS 2023] Imitation Improvement Learning for Large-Scale Capacitated Vehicle Routing Problems

Bui, V., & Mai, T. (2023, July). Imitation improvement learning for large-scale capacitated vehicle routing problems. In Proceedings of the International Conference on Automated Planning and Scheduling (Vol. 33, No. 1, pp. 551-559).

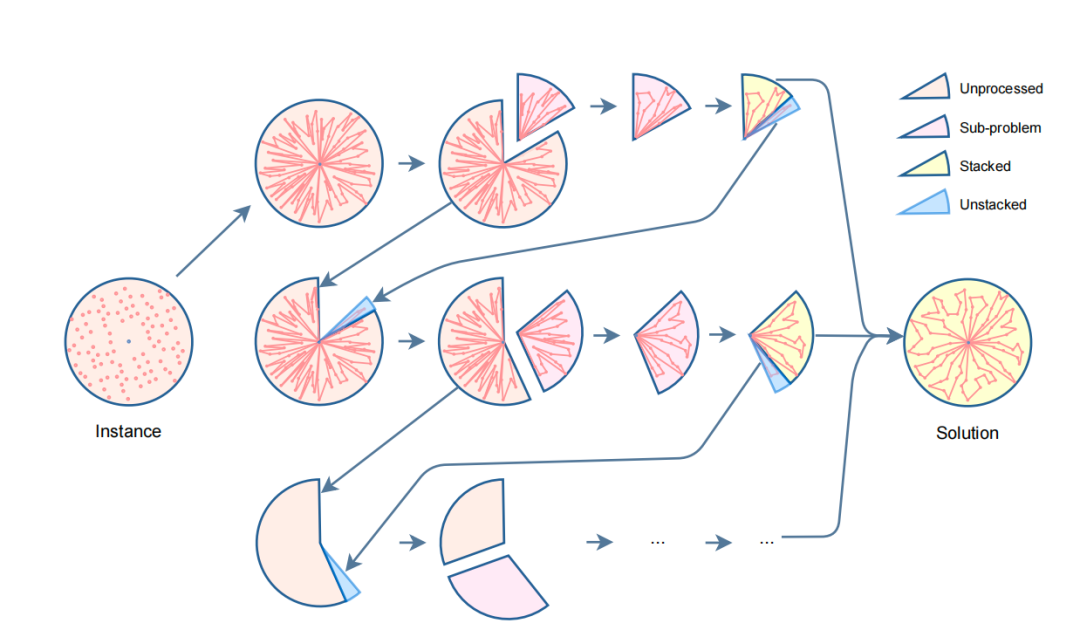
这篇文章提出了针对大规模cvrp问题的局部优化求解方案，其主要包含如下几个模块：

初始可行解构建：直接沿着clockwise方向将不同网点分配给不同的车，从而完成初始可行解的构建；
选择值得优化的子问题：沿着clockwise方向将挨着的k辆车的路线合并成1个待优化的子问题；
子问题求解：使用新设计的结合强化学习以及模仿学习范式的模型进行求解，考虑到模型构建的路线可能不是可行解，因此会使用启发式算法进行校正。其中，这篇文章提出的模型有2个优化目标：最大化长期收益（强化学习）以及尽可能模仿专家（启发式算法）的决策（模仿学习）。
可行解调整：当沿着clockwise方向走完一轮后，将优化过的子问题的解合并到一起，从而形成针对原始问题的完整可行解；

3. 调整模型结构

[Constraints 2022] Learning the Travelling Salesperson Problem Requires Rethinking Generalization

Joshi, C. K., Cappart, Q., Rousseau, L. M., & Laurent, T. (2022). Learning the travelling salesperson problem requires rethinking generalization. Constraints, 27(1), 70-98.

这篇文章主要从实验角度分析了不同学习范式、不同模型结构、不同norm、不同数据配比策略对模型泛化能力的影响，相关结论：

不同数据分布配比：在训练集中混合不同规模、不同分布的tsp问题，有助于提升其最终的泛化能力；
tsp graph构建：将full graph调整为边覆盖率20%～50%的knn graph，有助于提升效果；
图神经网络的信息聚合以及norm策略：当问题规模变大时，GNN-sum聚合的效果会明显变差。GNN-max和GNN-mean聚合的效果通常还不错；layernorm以及针对数据的batch-norm，通常效果优于不加norm；
AR vs NAR：对于decoder，AR（自回归）的泛化能力通常优于NAR（非自回归）；
不同学习范式：当解码策略为greedy时，强化学习模型的泛化能力通常要好于模仿学习模型。当解码策略为beam search时，则刚好相反；

[NIPS 2023] Neural Combinatorial Optimization with Heavy Decoder: Toward Large Scale Generalization

Luo, F., Lin, X., Liu, F., Zhang, Q., & Wang, Z. (2024). Neural combinatorial optimization with heavy decoder: Toward large scale generalization. Advances in Neural Information Processing Systems, 36.

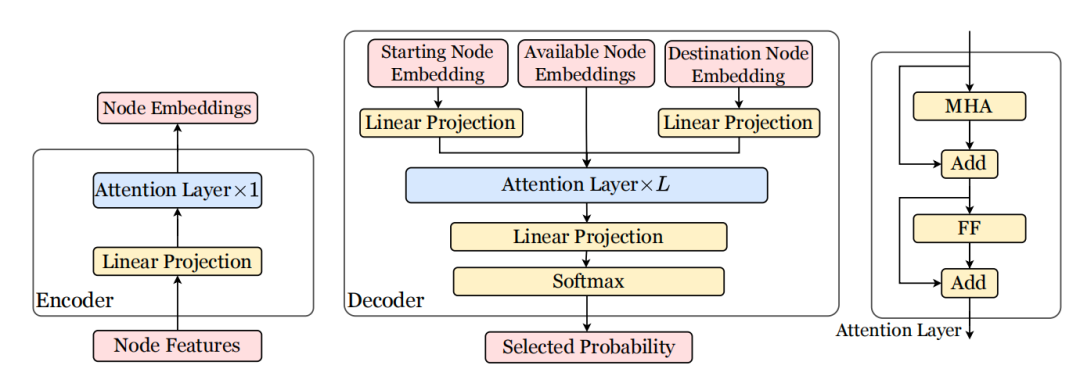
这篇文章针对大规模TSP/VRP问题提出了名为LEHD的模型，其特点是Light Encoder & Heavy Decoder。文章作者认为过往的模型之所以无法很好的求解大规模问题是因为它们的模型属于Heavy Encoder & Light Decoder，即过于复杂的encoder容易让模型对小规模的tsp/vrp产生过拟合问题，继而限制了其泛化到更大规模问题的能力。因此，作者们尝试简化encoder以及复杂化decoder。从最终的实验结果可知，本文提出的模型在大规模问题（TSP1000/CVRP1000）的求解上具有较好的泛化能力。

4. 调整学习范式：自学习

[Arxiv 2024] Self-Improved Learning for Scalable Neural Combinatorial Optimization

Luo, F., Lin, X., Wang, Z., Xialiang, T., Yuan, M., & Zhang, Q. (2024). Self-Improved Learning for Scalable Neural Combinatorial Optimization. arXiv preprint arXiv:2403.19561.

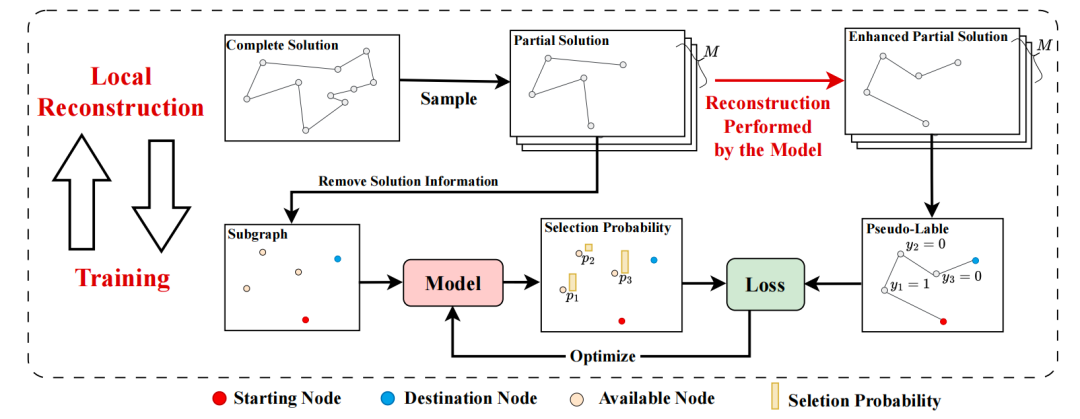
这篇文章提出了一种名为Self-Improved Learning (SIL) 的学习范式。这个范式的特点是模型的优化目标是由模型自己产出的，即不需要提前构建label而仅靠自提升的方式进行优化。除了包含常规的机器学习模型，SIL还引入了1个Local Reconstruct模块。Reconstruct模块和机器学习模型相互协同，前者会基于后者构建更好的部分可行解，而后者则会将前者构建的高质量解加入到后续的训练集中。Reconstruct模块包含2个部分：针对solution的子图抽样以及基于模型构建新的部分可行解。对于机器学习模型，其优化目标是在给定起点&终点节点的前提下预测一条较优路线。模型结构上，SIL沿用了经典的encoder-decoder框架，encoder负责对输入的subgraph进行建模，而decoder则负责依次预测下1个节点。为了加快大规模问题的求解，decoder中经常使用的self-attention被替换成新设计的linear-attention。这个优化非常关键，直接将核心模块的时间复杂度从O(N * N)降到了O(N)，从而大幅度降低了求解大规模优化问题所需的时间和资源。从最终的实验上看，SIL能在有限的时间内较好地求解TSP100K、CVRP100K等大规模路线规划问题。