240621_昇思学习打卡-Day3-余弦退火+周期性重启+warm up
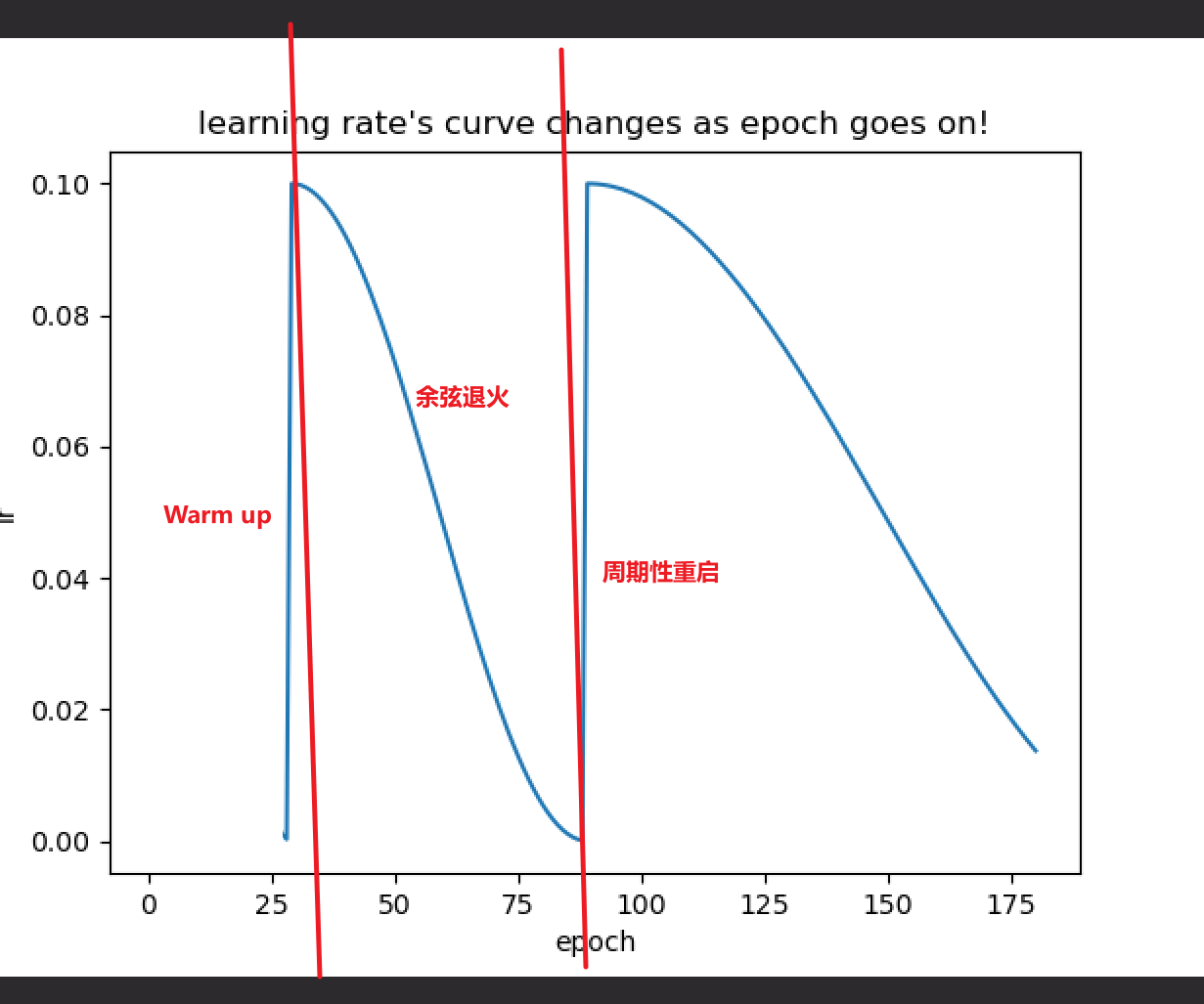
先展示一个完整的余弦退火+周期性重启+warm up调整学习率的流程(横轴为epoch,纵轴为学习率):
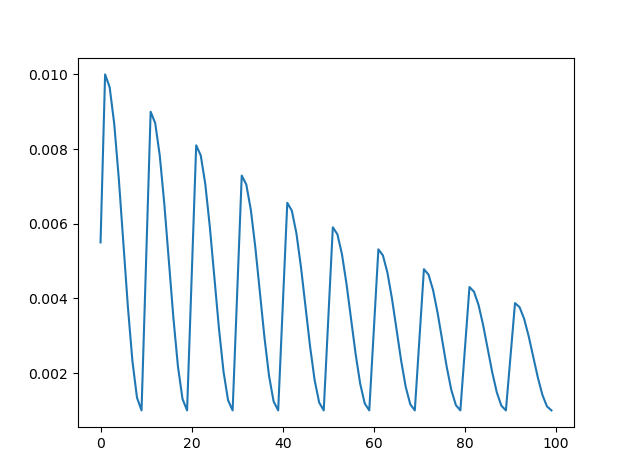
我们换一个收敛较慢的图进行详细说明:
Warm up
在神经网络刚开始训练时,梯度较大,如果一开始就设置比较大的学习率的话,训练会极不稳定,导致不能得到较好的收敛效果,所以我们需要在最开始训练时将学习率保持在一个比较低的水平,让梯度先收敛到一定程度,然后再把学习率增大,可以有效提高收敛效果。这个过程称为网络训练的预热(warm up)
def init_lr(self):
"""
初始化每个参数组的学习率。
"""
self.base_lrs = []
for param_group in self.optimizer.param_groups:
param_group['lr'] = self.min_lr
self.base_lrs.append(self.min_lr)
余弦退火
使用余弦函数可以达到一个较好的学习率衰减效果,具体来说,随着x的增加余弦值首先缓慢下降,然后加速下降,在即将到达极值点时收敛速度,缓慢靠近,这种下降模式与学习率配合可以得到很好的效果。这个过程就叫余弦退火。
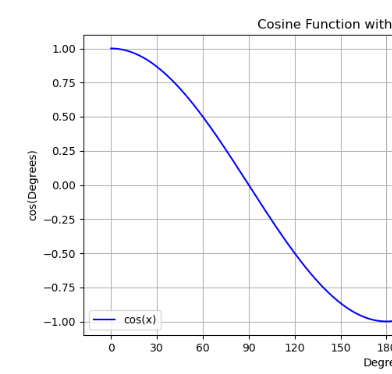

这一段本来是写的字,但是传到csdn不知道为什么编码就乱了,半夜了也不想深究了,直接截图上来吧

这部分的核心代码如下:
def get_lr(self):
"""
计算当前步骤的学习率。
返回:
- list: 当前步骤的学习率列表。
"""
if self.step_in_cycle == -1:
return self.base_lrs
elif self.step_in_cycle < self.warmup_steps:
# 线性warmup阶段
return [(self.max_lr - base_lr)*self.step_in_cycle / self.warmup_steps + base_lr for base_lr in self.base_lrs]
else:
# 余弦退火阶段,这么多代码其实就是上面那个公式
return [base_lr + (self.max_lr - base_lr) \
* (1 + math.cos(math.pi * (self.step_in_cycle-self.warmup_steps) \
/ (self.cur_cycle_steps - self.warmup_steps))) / 2
for base_lr in self.base_lrs]
周期性重启
在进行“一轮”(学习率收敛到较低点)学习之后,可能达到的极值点只是局部极小值,并不是全局最小值,现在就需要用到:学习率突然增大,跳出局部极小值,去寻找全局最小值,这个过程称为周期性重启。
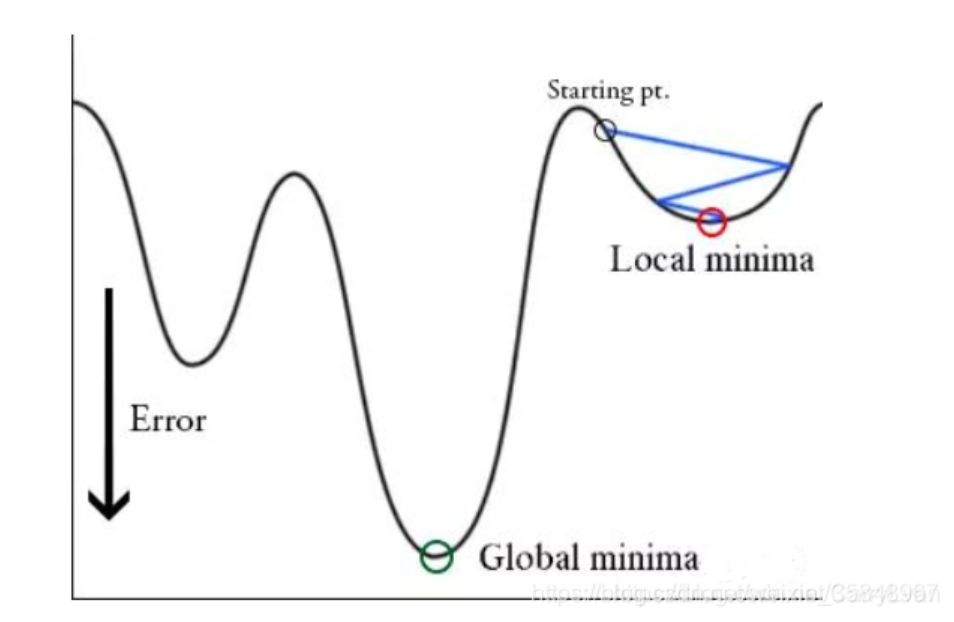
这里我们梳理一下整个流程:
在模型训练最开始时,因此时梯度较大,我们的学习率需要保持一个较低得水平,在梯度得到一定程度的收敛之后(比如两轮),学习率开始急速增大(warm up),然后为了靠近极值点,采用余弦退火进行学习率的调整,在学习率调整到较低点时(假设八轮),因此时不能保证是否为全局最小值,我们需要再让他跳出这个极值点,再去找有没有更优的极值点,这就是周期性重启(十轮一重启)。
以下就是周期性重启的核心代码:
def step(self, epoch=None):
"""
执行一步学习率调度。
参数:
- epoch (int, 可选): 当前周期。如果为None,则使用内部的last_epoch值并自增。
"""
if epoch is None:
# 自增步骤并检查是否需要重置周期
epoch = self.last_epoch + 1
self.step_in_cycle = self.step_in_cycle + 1
if self.step_in_cycle >= self.cur_cycle_steps:
self.cycle += 1
self.step_in_cycle = self.step_in_cycle - self.cur_cycle_steps
self.cur_cycle_steps = int((self.cur_cycle_steps - self.warmup_steps) * self.cycle_mult) + self.warmup_steps
else:
# 根据给定的epoch更新周期和步骤
if epoch >= self.first_cycle_steps:
if self.cycle_mult == 1.:
self.step_in_cycle = epoch % self.first_cycle_steps
self.cycle = epoch // self.first_cycle_steps
else:
n = int(math.log((epoch / self.first_cycle_steps * (self.cycle_mult - 1) + 1), self.cycle_mult))
self.cycle = n
self.step_in_cycle = epoch - int(self.first_cycle_steps * (self.cycle_mult ** n - 1) / (self.cycle_mult - 1))
self.cur_cycle_steps = self.first_cycle_steps * self.cycle_mult ** (n)
else:
self.cur_cycle_steps = self.first_cycle_steps
self.step_in_cycle = epoch
# 更新最大学习率
self.max_lr = self.base_max_lr * (self.gamma**self.cycle)
self.last_epoch = math.floor(epoch)
for param_group, lr in zip(self.optimizer.param_groups, self.get_lr()):
param_group['lr'] = lr
完整代码如下:
# 导入优化器模块和PyTorch的神经网络模块
import torch.optim as optim
import torch
import torch.nn as nn
from torch.optim import SGD
import math
import matplotlib.pyplot as plt
# 定义CosineAnnealingWarmupRestarts学习率调度器类
class CosineAnnealingWarmupRestarts(optim.lr_scheduler._LRScheduler):
"""
Cosine Annealing Warmup Restarts学习率调度器。
参数:
- optimizer (Optimizer): 包装的优化器。
- first_cycle_steps (int): 第一个周期的步数。
- cycle_mult (float): 周期步数的乘数。默认: 1.0。
- max_lr (float): 第一个周期的最大学习率。默认: 0.1。
- min_lr (float): 最小学习率。默认: 0.001。
- warmup_steps (int): 线性warmup的步数。默认: 0。
- gamma (float): 周期间最大学习率的减少率。默认: 1.0。
- last_epoch (int): 上一个周期的索引。默认: -1。
"""
def __init__(self,
optimizer: torch.optim.Optimizer,
first_cycle_steps: int,
cycle_mult: float = 1.,
max_lr: float = 0.1,
min_lr: float = 0.001,
warmup_steps: int = 0,
gamma: float = 1.,
last_epoch: int = -1
):
# 确保warmup步骤少于第一个周期的步骤
assert warmup_steps < first_cycle_steps
# 初始化各种参数
self.first_cycle_steps = first_cycle_steps # first cycle step size
self.cycle_mult = cycle_mult # cycle steps magnification
self.base_max_lr = max_lr # first max learning rate
self.max_lr = max_lr # max learning rate in the current cycle
self.min_lr = min_lr # min learning rate
self.warmup_steps = warmup_steps # warmup step size
self.gamma = gamma # decrease rate of max learning rate by cycle
# 当前周期的步数和周期计数
self.cur_cycle_steps = first_cycle_steps # first cycle step size
self.cycle = 0 # cycle count
self.step_in_cycle = last_epoch # step size of the current cycle
# 调用父类构造函数
super(CosineAnnealingWarmupRestarts, self).__init__(optimizer, last_epoch)
# 初始化学习率
self.init_lr()
# 初始化学习率的方法
def init_lr(self):
"""
初始化每个参数组的学习率。
"""
self.base_lrs = []
for param_group in self.optimizer.param_groups:
param_group['lr'] = self.min_lr
self.base_lrs.append(self.min_lr)
# 计算当前学习率的方法
def get_lr(self):
"""
计算当前步骤的学习率。
返回:
- list: 当前步骤的学习率列表。
"""
if self.step_in_cycle == -1:
return self.base_lrs
elif self.step_in_cycle < self.warmup_steps:
# 线性warmup阶段
return [(self.max_lr - base_lr)*self.step_in_cycle / self.warmup_steps + base_lr for base_lr in self.base_lrs]
else:
# Cosine Annealing阶段
return [base_lr + (self.max_lr - base_lr) \
* (1 + math.cos(math.pi * (self.step_in_cycle-self.warmup_steps) \
/ (self.cur_cycle_steps - self.warmup_steps))) / 2
for base_lr in self.base_lrs]
# 执行一步学习率调度的方法
def step(self, epoch=None):
"""
执行一步学习率调度。
参数:
- epoch (int, 可选): 当前周期。如果为None,则使用内部的last_epoch值并自增。
"""
if epoch is None:
# 自增步骤并检查是否需要重置周期
epoch = self.last_epoch + 1
self.step_in_cycle = self.step_in_cycle + 1
if self.step_in_cycle >= self.cur_cycle_steps:
self.cycle += 1
self.step_in_cycle = self.step_in_cycle - self.cur_cycle_steps
self.cur_cycle_steps = int((self.cur_cycle_steps - self.warmup_steps) * self.cycle_mult) + self.warmup_steps
else:
# 根据给定的epoch更新周期和步骤
if epoch >= self.first_cycle_steps:
if self.cycle_mult == 1.:
self.step_in_cycle = epoch % self.first_cycle_steps
self.cycle = epoch // self.first_cycle_steps
else:
n = int(math.log((epoch / self.first_cycle_steps * (self.cycle_mult - 1) + 1), self.cycle_mult))
self.cycle = n
self.step_in_cycle = epoch - int(self.first_cycle_steps * (self.cycle_mult ** n - 1) / (self.cycle_mult - 1))
self.cur_cycle_steps = self.first_cycle_steps * self.cycle_mult ** (n)
else:
self.cur_cycle_steps = self.first_cycle_steps
self.step_in_cycle = epoch
# 更新最大学习率
self.max_lr = self.base_max_lr * (self.gamma**self.cycle)
self.last_epoch = math.floor(epoch)
for param_group, lr in zip(self.optimizer.param_groups, self.get_lr()):
param_group['lr'] = lr
# 创建一个简单的线性模型和SGD优化器
# 构建一个简单的模型和优化器
model = nn.Linear(10, 1) # 简单的线性层作为示例模型
optimizer = SGD(model.parameters(), lr=0.1) # 初始化优化器,lr参数会被调度器覆盖
# 实例化学习率调度器
# 实例化学习率调度器
scheduler = CosineAnnealingWarmupRestarts(optimizer,
first_cycle_steps=10,
cycle_mult=1.,
max_lr=0.01,
min_lr=0.001,
warmup_steps=2,
gamma=0.9)
# 打印初始学习率
print("Initial LR:", scheduler.get_lr())
# 记录学习率的变化
loss_list=[]
# 模拟训练过程中的学习率变化
# 模拟几个周期的训练步骤
for epoch in range(100): # 总共运行25个epoch
scheduler.step() # 更新学习率
lrs = scheduler.get_lr()
loss_list.append(lrs)
print(f"Epoch {epoch}: LR(s) -> {lrs}")
# 绘制学习率变化图
x=list(range(100))
plt.figure()
plt.plot(x,loss_list)
plt.show()
打卡记录:



![[MySql]两阶段提交](https://img-blog.csdnimg.cn/direct/522baae819664d9493032a1e212ef021.png)