传送门

A. X Axis

时间限制：2秒        空间限制：256MB        输入：标准输入        输出：标准输出

问题描述

你有三个位于 X 轴上的整数坐标点 , 和 （其中 ）。你可以选择 X 轴上任意一个整数坐标点 a。注意，点 a 可以与 , 或 重合。定义 f(a) 为从给定的点到点 a 的总距离。找出 f(a) 的最小值。

两个点 a 和 b 之间的距离等于 ∣a−b∣。例如，点 a = 5 和 b = 2 之间的距离为 3。

输入格式

每个测试包含多个测试用例。第一行包含一个整数 t（），表示测试用例的数量。接下来是每个测试用例的描述。

每个测试用例的一行包含三个整数 , 和 （），表示这些点的坐标。

输出格式

对于每个测试用例，输出 f(a) 的最小值。

样例输入

样例输出

注释

在第一个测试用例中，当 a = 1 时，f(a) 的最小值为：f(1) = |1 - 1| + |1 - 1| + |1 - 1| = 0。

在第二个测试用例中，当 a = 5 时，f(a) 的最小值为：f(5) = |1 - 5| + |5 - 5| + |9 - 5| = 8。

在第三个测试用例中，当 a = 8 时，f(a) 的最小值为：f(8) = |8 - 8| + |2 - 8| + |8 - 8| = 6。

在第四个测试用例中，当 a = 9 时，f(a) 的最小值为：f(10) = |10 - 9| + |9 - 9| + |3 - 9| = 7。

思路

数据量非常小，所以从最小的  开始遍历到最大的 ，并找出这中间最小的 f(a) 即可。

代码

#include <bits/stdc++.h>
using namespace std;
inline int read() {
    int x = 0, f = 1; char c = getchar();
    while (c < '0' || c > '9') { if (c == '-') f = -1; c = getchar(); }
    while (c >= '0' && c <= '9') x = x * 10 + c - '0', c = getchar();
    return x * f;
}
int main () {
    int t = read();
    while (t--) {
        int x1 = read(), x2 = read(), x3 = read(), ans = INT_MAX;
        int minm = min(x1, min(x2, x3)), maxm = max(x1, max(x2, x3));
        for (int i = minm; i <= maxm; i++) {
            ans = min(ans, abs(i - x1) + abs(i - x2) + abs(i - x3));
        }
        printf("%d\n", ans);
    }
    return 0;
}

B. Matrix Stabilization

时间限制：2秒        空间限制：256MB        输入：标准输入        输出：标准输出

问题描述

你有一个大小为  的矩阵，其中行从上到下编号为 1 到 n，列从左到右编号为 1 到 m。第 i 行和第 j 列交叉处的元素记为 。

考虑如下用于稳定矩阵 a 的算法：

1. 找到一个单元格 ，其值严格大于所有相邻单元格的值。如果没有这样的单元格，终止算法。如果有多个这样的单元格，选择 i 值最小的那个，如果仍有多个单元格，选择 j 值最小的那个。
2. 将 设置为 。
3. 回到第1步。

在这个问题中，如果两个单元格 和 共享一个公共边，则它们被认为是相邻的，即 |a - c| + |b - d| = 1。

你的任务是输出矩阵 a 在算法执行完毕后的状态。可以证明，该算法不能无限次执行。

输入格式

每个测试包含多组输入数据。第一行包含一个整数 t ()，表示输入数据的组数。接下来是每组输入数据的描述。

每组输入数据的第一行包含两个整数 n 和 m ()，表示矩阵 a 的行数和列数。

接下来的 n 行描述了矩阵的对应行。第 i 行包含 m 个整数  ()。

保证所有输入数据组的 之和不超过 。

输出格式

对于每组输入数据，输出 n 行，每行包含 m 个数字，表示在稳定算法执行后的矩阵 a 的各个单元格的值。

样例输入

样例输出

注释

在第一组输入数据中，算法将连续两次选择单元格 (1,1)，然后终止。

在第二组输入数据中，没有单元格的值严格大于所有相邻单元格的值。

在第三组输入数据中，算法将选择单元格 (2,2)，然后终止。

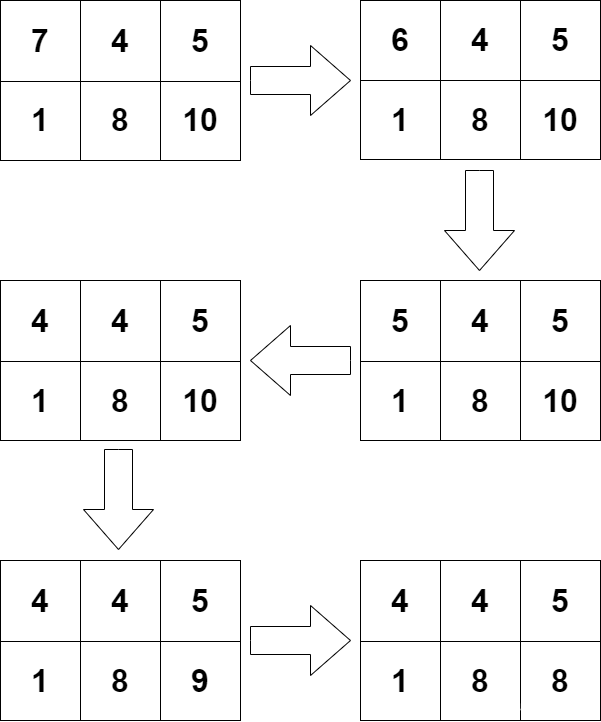
在第四组输入数据中，算法将选择单元格 (1,1) 三次，然后选择单元格 (2,3) 两次。

思路

将矩阵遍历一遍，对于单元格，如果它的值每个严格大于周围单元格的值，那么将它打值改为周围单元格最大的值。

代码

#include <bits/stdc++.h>
using namespace std;
int t, n, m, a[105][105];
const int dx[] = {0, 0, 1, -1}, dy[] = {1, -1, 0, 0};
inline int read() {
    int x = 0, f = 1; char c = getchar();
    while (c < '0' || c > '9') { if (c == '-') f = -1; c = getchar(); }
    while (c >= '0' && c <= '9') x = x * 10 + c - '0', c = getchar();
    return x * f;
}

int main () {
    t = read();
    while (t--) {
        n = read(), m = read();
        for (int i = 1; i <= n; i++)
            for (int j = 1; j <= m; j++) a[i][j] = read();
        for (int i = 1; i <= n; i++) {
            for (int j = 1; j <= m; j++) {
                int flag = 1, temp = 0;
                for (int k = 0; k < 4; k++) {
                    int x = i + dx[k], y = j + dy[k];
                    if (x < 1 || x > n || y < 1 || y > m) continue;
                    if (a[x][y] >= a[i][j]) flag = 0;
                    temp = max(temp, a[x][y]);
                }
                if (flag) a[i][j] = temp;
            }
        }
        for (int i = 1; i <= n; i++) {
            for (int j = 1; j <= m; j++) {
                printf("%d ", a[i][j]);
            }
            putchar('\n');
        }
    }
    return 0;
}

C. Update Queries

时间限制：2秒        空间限制：256MB        输入：标准输入        输出：标准输出

问题描述

让我们考虑下面这个简单的问题。你有一个长度为 n 的字符串 s，由小写拉丁字母组成，同时有一个长度为 m 的索引数组 ind () 和一个长度为 m 的字符串 \( c \)，由小写拉丁字母组成。然后，依次执行更新操作，即在第 i 次操作中，将 。注意，你需要从第一个操作到最后一个操作按顺序执行所有的 m 次操作。

当然，如果你改变数组 ind 中的索引顺序和，或字符串 c 中字母的顺序，你可能会得到不同的结果。找出在 m 次更新操作之后，可以得到的按字典序最小的字符串 s ，如果你可以随意重新排列数组 ind 中的索引和字符串 c 中的字母。

字符串 a 按字典序小于字符串 b 的条件如下：

1. a 是 b 的前缀，但 ；
2. 在 a 和 b 不同的第一个位置，字符串 a 中的字符在字母表中的顺序早于字符串 b 中的对应字符。

输入格式

每个测试包含多个输入数据集。第一行包含一个整数 t ()，表示输入数据集的数量。接下来是各个数据集的描述。

每个输入数据集的第一行包含两个整数 n 和 m ()，分别表示字符串 s 的长度和更新操作的数量。

每个输入数据集的第二行包含一个长度为 n 的字符串 s，由小写拉丁字母组成。

每个输入数据集的第三行包含 m 个整数  ()，表示索引数组 ind。

每个输入数据集的第四行包含一个长度为 m 的字符串 c，由小写拉丁字母组成。

保证所有输入数据集的字符串长度 n 之和不超过 。同样地，所有输入数据集的更新操作数量 m 之和不超过 。

输出格式

对于每组输入数据，输出通过重新排列索引数组 ind 和字符串 c 中的字母后可以得到的按字典序最小的字符串 s。

样例输入

样例输出

注释

在第一组输入数据中，你可以保持数组 ind 和字符串 c 不变，按照它们原始的顺序执行所有操作。

在第二组输入数据中，你可以设置数组 ind = [1, 1, 4, 2]，并且 c = "zczw"。然后字符串 s 的变化如下：meow→zeow→ceow→ceoz→cwoz。

在第三组输入数据中，你可以保持数组 ind 不变，并设置 c = "admn"。然后字符串 s 的变化如下：abacaba→abacaba→abdcaba→abdcmba→abdcmbn。

思路

贪心的考虑，要让字符串的字典序最小，那么就要让每个字符串靠前的字符的字典序要尽量小。我们只需要对 ind 数组排序并且去重，对字符串 c 排序之后，再对字符串 s 依次进行修改即可。

代码

#include <bits/stdc++.h>
using namespace std;
const int N = 1e5 + 10;
int t, n, m, idx[N], b[N];
char s[N], c[N];
inline int read() {
    int x = 0, f = 1; char c = getchar();
    while (c < '0' || c > '9') { if (c == '-') f = -1; c = getchar(); }
    while (c >= '0' && c <= '9') x = x * 10 + c - '0', c = getchar();
    return x * f;
}
int main () {
    t = read();
    while (t--) {
        n = read(), m = read();
        scanf("%s", s);
        for (int i = 1; i <= m; i++) idx[i] = read();
        scanf("%s", c);
        for (int i = 0; i < m; i++) b[i] = c[i] - 'a';
        sort(idx + 1, idx + m + 1), sort(b, b + m);
        int size = unique(idx + 1, idx + m + 1) - idx - 1;
        for (int i = 1; i <= size; i++) s[idx[i] - 1] = b[i - 1] + 'a';
        printf("%s\n", s);
    }
    return 0;
}