双指针
b站UP主蜜糖:由于数据特征的有序性(大小或者正负),所以可以证明当前节点一定是优于过往节点,从而可以通过数据的维度数量的指针,逐步的迭代收敛最终找到最优解。
283.移动零
相关标签 : 数组 双指针 难度 : 简单
给定一个数组 nums,编写一个函数将所有 0 移动到数组的末尾,同时保持非零元素的相对顺序。
请注意 ,必须在不复制数组的情况下原地对数组进行操作。
示例 1:
输入: nums = [0,1,0,3,12]
输出: [1,3,12,0,0]
示例 2:
输入: nums = [0]
输出: [0]
提示:
1 <= nums.length <= 104-231 <= nums[i] <= 231 - 1
进阶: 你能尽量减少完成的操作次数吗?
解析:
原地 :不能新建数组
一开始的想法:
1.判断每个节点是不是为0
2.把其他数值都挪动 【需要优化】
3.将0挪到最后面
这里其实很麻烦,假如第一个数就是0。那你把0挪到最后面,一开始他后面的数字都往前挪了一位。但是这些数字都没有被判断过,挪了后又得判断,很浪费时间。这得n^2的复杂度了。
1.双指针 交换
左指针指向当前已经处理好的序列的尾部, 右指针指向待处理序列的头部
左节点是存了为0的节点,右节点是选择到最新不为0的节点,用来替换。
public void moveZeroes(int[] nums) {
// 左指针指向当前已经处理好的序列的尾部, 右指针指向待处理序列的头部
int n = nums.length, left = 0, right = 0;
// 从头开始处理,处理到最后一个数
// 为0的话,左指针就直接记录下来为0的那个节点的(因为这里是每次都先将left+1,实则指向下一个节点)
// 然后等到不为0时,右指针已经指向了不为0节点。此时只需要将当前不为0的节点与为0的节点替换就行了。
// 等于左节点是存了为0的节点,右节点是选择到最新不为0的节点。来替换的。因此需要先将左节点++可以锁定,然后右节点开始找。
while (right < n) {
if (nums[right] != 0) {
swap(nums, left, right);
left++;
}
right++;
}
}
// 交换代码
public void swap(int[] nums, int left, int right) {
int temp = nums[left];
nums[left] = nums[right];
nums[right] = temp;
}
// 目标节点,也就是为0的节点
int index = 0;
int count = nums.length;
// 让指针从头走到尾,i就记录当前节点
for (int i = 0; i < count; i++) {
// 假如指针所指的值为0,index指向的就是为0的节点。
// 假如第一个为0,那这个时候index也就是指向0的。
// 为了能使index指向0,所以它要比i早+1,然后假如正常的话就无所谓了,继续加就行。
// 这里当指向0的时候,直接跳转到不为0的点
if (nums[i] == 0){
continue;
}
// 不为0就正常不理就行。但是这个代码主要是针对假如跳转到不为0的点后,就覆盖掉原来为0的点【index指向的就是为0的节点】
//
if (index < i) {
nums[index] = nums[i];
}
index ++;
}
//前面的那一块已经把不为0的都按顺序挪好了,然后处理完后的节点就都补0
for (int i = index; i < count; i++) {
//最后的时候index就是已经指向了
nums[i] = 0;
}
11.盛最多水的容器
相关标签 :贪心 数组 双指针 难度 : 中等
给定一个长度为 n 的整数数组 height 。有 n 条垂线,第 i 条线的两个端点是 (i, 0) 和 (i, height[i]) 。
找出其中的两条线,使得它们与 x 轴共同构成的容器可以容纳最多的水。
返回容器可以储存的最大水量。
**说明:**你不能倾斜容器。
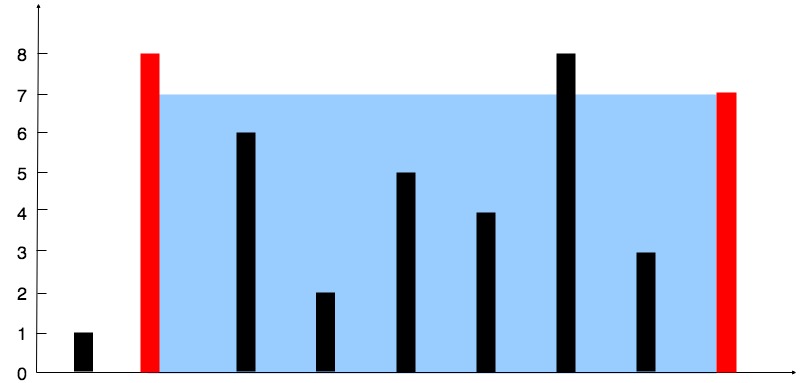
输入:[1,8,6,2,5,4,8,3,7]
输出:49
解释:图中垂直线代表输入数组 [1,8,6,2,5,4,8,3,7]。在此情况下,容器能够容纳水(表示为蓝色部分)的最大值为 49。
示例 2:
输入:height = [1,1]
输出:1
提示:
n == height.length2 <= n <= 1050 <= height[i] <= 104
解析:
这里面其实就是看容器的左右两边,他是一个短板效应;水的高度代表着这个容器的宽度了。整体的容器面积等于:左右两边高度较短的一边 min(height[i] , height[j]) × 底边的宽度(W) 【长方形面积公式】
根据判断容积的公式定义字段来计算,循环下去计算,然后存下来最大容积就行了。
【这里的双指针就是用于指定左右边界,就是这个容器的两边,用来方便计算】
public int maxArea(int[] height) {
// 根据判断容积的公式定义字段来计算
// 临时容积
int tempArea = 0;
// 左边的柱子
int left = 0;
// 右边的柱子
int right = height.length - 1;
// 最终返回结果
int area = 0;
// 不断判断左右两边柱子的长度,较小的柱子进行移动,计算并收集最长的容积
while (left < right) {
// 先计算,然后每次移动完接着计算
tempArea = Math.min(height[left], height[right]) * (right - left);
area = Math.max(tempArea, area);
// 判断那边短,就那边移动
if (height[left] < height[right]) {
left++;
} else {
right--;
}
}
return area;
}
15.三数之和
相关标签 :数组 双指针 排序 难度 : 中等
给你一个整数数组 nums ,判断是否存在三元组 [nums[i], nums[j], nums[k]] 满足 i != j、i != k 且 j != k ,同时还满足 nums[i] + nums[j] + nums[k] == 0 。请
你返回所有和为 0 且不重复的三元组。
**注意:**答案中不可以包含重复的三元组。
示例 1:
输入:nums = [-1,0,1,2,-1,-4]
输出:[[-1,-1,2],[-1,0,1]]
解释:
nums[0] + nums[1] + nums[2] = (-1) + 0 + 1 = 0 。
nums[1] + nums[2] + nums[4] = 0 + 1 + (-1) = 0 。
nums[0] + nums[3] + nums[4] = (-1) + 2 + (-1) = 0 。
不同的三元组是 [-1,0,1] 和 [-1,-1,2] 。
注意,输出的顺序和三元组的顺序并不重要。
示例 2:
输入:nums = [0,1,1]
输出:[]
解释:唯一可能的三元组和不为 0 。
示例 3:
输入:nums = [0,0,0]
输出:[[0,0,0]]
解释:唯一可能的三元组和为 0 。
提示:
3 <= nums.length <= 3000-105 <= nums[i] <= 105
解析:
这里不能使用哈希。因为他需要返回多组答案,哈希的性质是:
键值对存储:我们通常只关心键(即元素本身),而不关心元素的组合。
实则就是做:查询两个和为0的数,并且返回所有结果,然后还要去重。
1.第一个循环进行的是固定一个值,移动他下一个值和结尾的值,判断相加为0。
int sum = nums[i] + nums[left] + nums[right];
2.排好序了,然后去重就是内外循环都判断是不是指针所指的值是不是一样的。
public static List<List<Integer>> threeSum(int[] nums) {
ArrayList<List<Integer>> result = new ArrayList<>();
if (nums == null || nums.length < 3) {
return result;
}
Arrays.sort(nums);
// 这里i < nums.length - 2,代表数的返回只用判断到倒数第三位。因为至少有两个元素在它之后来形成一个三元组
for (int i = 0; i < nums.length - 2; i++) {
if (i > 0 && nums[i] == nums[i - 1]) {
continue;
}
int left = i + 1;
int right = nums.length - 1;
while (left < right) {
int sum = nums[i] + nums[left] + nums[right];
// 去重需要内循环和外循环都做判断。
if (sum == 0) {
result.add(Arrays.asList(nums[i], nums[left], nums[right]));
// 当你找到一个和为0的三元组时,需要移动指针,继续判断。
// 需要移动两个指针,因为已经有了这个结果了。你只移动一个,结果都还是一样的,等于确定了2个数,第三个肯定是固定的。
left++;
right--;
// 跳过重复的元素
// 因为都是排好序的,假如相同的话,那么都是连在一起的
// 这里属于内循环判断。
while (left < right && nums[left] == nums[left - 1]) {
left++;
}
while (left < right && nums[right] == nums[right + 1]) {
right--;
}
// 这里假如和小于0,因为right指向的是最大的值了,无法在提升。就让left移动,增加值的大小
} else if (sum < 0) {
left++;
} else {
right++;
}
}
}
return result;
}
42.接雨水
相关标签 :栈 数组 双指针 动态规划 单调栈 难度 : 困难
给定 n 个非负整数表示每个宽度为 1 的柱子的高度图,计算按此排列的柱子,下雨之后能接多少雨水。

输入:height = [0,1,0,2,1,0,1,3,2,1,2,1]
输出:6
解释:上面是由数组 [0,1,0,2,1,0,1,3,2,1,2,1] 表示的高度图,在这种情况下,可以接 6 个单位的雨水(蓝色部分表示雨水)。
示例 2:
输入:height = [4,2,0,3,2,5]
输出:9
提示:
n == height.length1 <= n <= 2 * 1040 <= height[i] <= 105
【单调栈】
做这道题之前可以先看看其他的题目,有着一曲共同之妙。 【单调栈】
【单调栈】 适合解决 求当前元素左边或者右边第一个比当前元素大或者小的元素。
简单来说就是 栈(先进后出)里面元素是保证单调递增或者单调递减
LeetCode 739 每日温度
标签:栈 数组 单调栈 难度: 中等
给定一个整数数组 temperatures ,表示每天的温度,返回一个数组 answer ,其中 answer[i] 是指对于第 i 天,下一个更高温度出现在几天后。如果气温在这之后都不会升高,请在该位置用 0 来代替。
示例 1:
输入: temperatures = [73,74,75,71,69,72,76,73]
输出: [1,1,4,2,1,1,0,0]
示例 2:
输入: temperatures = [30,40,50,60]
输出: [1,1,1,0]
示例 3:
输入: temperatures = [30,60,90]
输出: [1,1,0]
提示:
1 <= temperatures.length <= 10530 <= temperatures[i] <= 100
知道单调栈的应用场景,那么这道题很明显就是可以直接使用单调栈来解决。
【单调栈 适合解决 求当前元素左边或者右边第一个比当前元素大或者小的元素。】
1.决定单调栈里面放什么内容。
这里在栈里面放元素的下标 【索引】(方便去计算元素的距离差值,根据题目的要求)
2.决定单调栈是要递增还是递减
这里通过需求,假如递增,那么就是求右边第一个比当前元素大的值。因为是单调递增的,递减就是需要求右边第一个比当前元素小的值。
单调栈初始值设置为 0 ,初始化栈。存的是下标值,然后是第一个数的下标,这样到时候返回也是0,没问题。

然后开始运行单调栈的逻辑:
遍历数组的i的值与栈顶的值对比大小。
小于的时候,就进行存入单调栈中。

大于的时候,
这个时候可以进行 当前值的下标值 - 栈顶的下标值 = 就等于相差的天数

然后因为栈顶是按照单调递增的【越往后越大】,后面的数也可以进行比较,假如大就继续pop和记录。假如小于栈顶的值,那么肯定也比后面的值小,直接放 push 进去栈就行了。
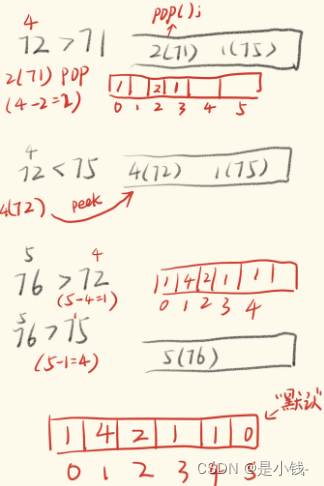
因为后面可能有些值没pop出去,还在栈里面。但是数组定义了大小的,那些没弹出的,数组就默认为0了
代码实现:
public int[] dailyTemperatures(int[] temperatures) {
// 获取数组的长度,定义一个结果数组。(长度是一样大的)
int length = temperatures.length;
int[] result = new int[length];
// 单调栈
LinkedList<Integer> stack = new LinkedList<>();
// 单调栈初始值设置为 0 ,初始化栈。
stack.push(0);
// 遍历数组中的每一个值
for (int i = 0; i < length; i++) {
// 假如新的数小于或者等于【栈顶】的值,就将它的下标存进去。反正是具有单调性的
if (temperatures[i] <= temperatures[stack.peek()]) {
stack.push(i);
// 假如新的值大于【栈顶】的值,那么说明找到了第一个比它大的值
// 这个时候可以进行 当前值的下标值 - 栈顶的下标值 = 就等于相差的天数
// 然后因为栈顶是按照单调递增的【越往后越大】,后面的数也可以进行比较,假如大就继续pop和记录。假如小于栈顶的值,那么肯定也比后面的值小,直接放 push 进去栈就行了。
} else {
while (!stack.isEmpty() && temperatures[i] > temperatures[stack.peek()]) {
result[stack.peek()] = i - stack.peek();
stack.pop();
}
stack.push(i);
}
}
// 因为后面可能有些值没pop出去,还在栈里面。但是数组定义了大小的,那些没弹出的,数组就默认为0了
return result;
}
然后回到刚刚的接雨水题目:

这里可以先用暴力解法理清楚思路:
就两次for循环,第一循环这个数组【模拟让每一个数组的值为底】,第二个是找到左边和右边第一个比它大的值中较小的那个值【短板效应 面积公式依旧是 min(h1,h2) * x(宽)】 (这样就是把自己作为一个凹槽,把全部的凹槽加起来,就是总的了)
然后这里就出现了单调栈的应用场景了:【单调栈】 适合解决 求当前元素左边或者右边第一个比当前元素大或者小的元素。

直接用题目的意思,然后存的话就继续存下标就行了。逻辑和之前的基本差不多,就是当遇到比栈顶大的时候,就把 i 的值 和栈顶后面的元素【 pop()以后再peek() 就是了】取一个较小值【短板】为 h ,宽就是下标相减,然后再-1 就是当前的宽 h*w = 面积。
接雨水代码实现:
class Solution {
public int trap(int[] height) {
int size = height.length;
if (size <= 2)
return 0;
Stack<Integer> stack = new Stack<>();
stack.push(0);
int result = 0;
for (int i = 1; i < size; i++) {
if (height[i] < height[stack.peek()]) {
stack.push(i);
} else if (height[i] == height[stack.peek()]) {
stack.pop();
stack.push(i);
} else {
while (!stack.isEmpty() && (height[i] > height[stack.peek()])) {
int mid = stack.pop();
if (!stack.isEmpty()) {
int left = stack.peek();
int h = Math.min(height[left], height[i]) - height[mid];
int w = i - left - 1;
int s = h * w;
if (s > 0)
result = result + s;
}
}
stack.push(i);
}
}
return result;
}
}
下面这道题就很类似接雨水,可以多做巩固一下:
LeetCode 84 柱状图中最大的矩形
标签:栈 数组 单调栈 难度: 困难
给定 n 个非负整数,用来表示柱状图中各个柱子的高度。每个柱子彼此相邻,且宽度为 1 。
求在该柱状图中,能够勾勒出来的矩形的最大面积。
示例 1:
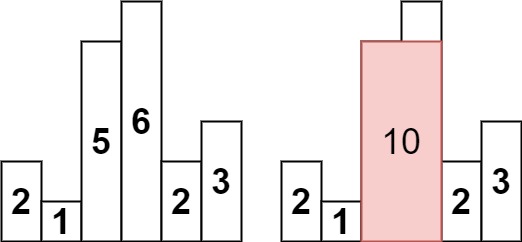
输入:heights = [2,1,5,6,2,3]
输出:10
解释:最大的矩形为图中红色区域,面积为 10
示例 2:
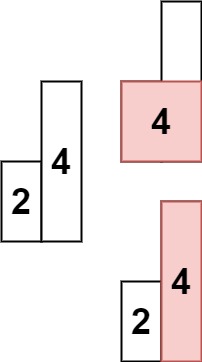
输入: heights = [2,4]
输出: 4
提示:
1 <= heights.length <=1050 <= heights[i] <= 104
其实这道题的题意很清晰易懂,也容易知道大概的方向,就是做起来比较麻烦。
矩形的面积就是:长(x轴为底) * 宽 (y轴为宽)
要想面积最大,要么就是长最长,宽最宽。
其实一次做过来,看上面的图,感觉就是遍历每一个下标的方块,然后他要是找到它左右两边第一个比自己小的话,那就是它所能构成最大的值了,假如没比自己小的,那就是自己了。
此题的特点: 给数组首尾都加了一个元素 0
因为假如数组刚好是单调递增的话,那么入栈以后,就是刚刚好单调递减。就都不会有计算面积的情况了。所以这个时候需要在数组的尾部加一个0,这样就可以计算 面积了。
假如一开始数组里面就是单调递减的,那么第二个数入栈判断就开始计算面积了,可是计算面积需要3个元素,而且栈顶元素出栈,栈会有空的情况,所以需要在数组头部加一个0。
【当前的高 * (前一个比自己矮的,后一个比自己矮的 两者下标之差 - 1)】
int largestRectangleArea(int[] heights) {
Stack<Integer> stack = new Stack<Integer>();
// 数组扩容,在头和尾各加入一个元素
int[] newHeights = new int[heights.length + 2];
// 这里是为了应对上诉的两种情况。
newHeights[0] = 0;
newHeights[newHeights.length - 1] = 0;
for (int i = 0; i < heights.length; i++) {
newHeights[i + 1] = heights[i];
}
heights = newHeights;
stack.push(0);
int result = 0;
//后续操作基本就是常规的了,明白面积公式即可,
for (int i = 0; i < heights.length; i++) {
if (heights[i] > heights[stack.peek()]) {
stack.push(i);
} else if (heights[i] == heights[stack.peek()]) {
stack.pop();
stack.push(i);
} else {
while (heights[i] < heights[stack.peek()]) {
int mid = stack.peek();
stack.pop();
int left = stack.peek();
int right = i;
int w = right - left - 1;
int h = heights[mid];
result = Math.max(result, w * h);
}
stack.push(i);
}
}
return result;
}
496.下一个更大元素 I
标签:栈 数组 哈希表 单调栈 难度: 简单
nums1 中数字 x 的 下一个更大元素 是指 x 在 nums2 中对应位置 右侧 的 第一个 比 x 大的元素。
给你两个 没有重复元素 的数组 nums1 和 nums2 ,下标从 0 开始计数,其中nums1 是 nums2 的子集。
对于每个 0 <= i < nums1.length ,找出满足 nums1[i] == nums2[j] 的下标 j ,并且在 nums2 确定 nums2[j] 的 下一个更大元素 。如果不存在下一个更大元素,那么本次查询的答案是 -1 。
返回一个长度为 nums1.length 的数组 ans 作为答案,满足 ans[i] 是如上所述的 下一个更大元素 。
示例 1:
输入:nums1 = [4,1,2], nums2 = [1,3,4,2].
输出:[-1,3,-1]
解释:nums1 中每个值的下一个更大元素如下所述:
- 4 ,用加粗斜体标识,nums2 = [1,3,4,2]。不存在下一个更大元素,所以答案是 -1 。
- 1 ,用加粗斜体标识,nums2 = [1,3,4,2]。下一个更大元素是 3 。
- 2 ,用加粗斜体标识,nums2 = [1,3,4,2]。不存在下一个更大元素,所以答案是 -1 。
示例 2:
输入:nums1 = [2,4], nums2 = [1,2,3,4].
输出:[3,-1]
解释:nums1 中每个值的下一个更大元素如下所述:
- 2 ,用加粗斜体标识,nums2 = [1,2,3,4]。下一个更大元素是 3 。
- 4 ,用加粗斜体标识,nums2 = [1,2,3,4]。不存在下一个更大元素,所以答案是 -1 。
提示:
1 <= nums1.length <= nums2.length <= 10000 <= nums1[i], nums2[i] <= 104nums1和nums2中所有整数 互不相同nums1中的所有整数同样出现在nums2中
**进阶:**你可以设计一个时间复杂度为 O(nums1.length + nums2.length) 的解决方案吗?
一看题目第一眼,下一个更大元素。这个就很容易让人想起单调栈。
nums1 = [4,1,2], nums2 = [1,3,4,2].
比如 4 ,找到nums1[i] == nums2[j] 的下标 j。
nums2 = [1,3,4,2]。 不存在下一个更大元素,所以答案是 -1 。
然后需要定义一个数组存储结果,而数组的大小自然就是nums1的大小,因为是根据nums1的每个数据进行判断的。而对于这个数组的初始值,因为假如没有比他大的就为-1,这个意味着单调栈的数据没有进到这个数组中,那么就得给这个数组设置一个默认的初始值 -1。
int[] res = new int[nums1.length];
Stack<Integer> stack = new Stack<>();
// 不存在对应位置就输出 -1 ,所以result数组如果某位置没有被赋值,那么就应该是是-1,所以就初始化为-1。
Arrays.fill(res, -1);
接着就是需要有判断nums2[i]是否在nums1中出现过这个点,这里可以用到hashmap,快速进行查询。
**一般哈希表都是用来快速判断一个元素是否出现集合里。**没有重复元素
HashMap<Integer, Integer> map = new HashMap<>();
for (int i = 0; i < nums1.length; i++) {
map.put(nums1[i], i);
}
而后后续就是利用单调栈,然后单调递增,遇到比栈顶大的,就进行pop,并且判断该数是否存在于nums1中,然后根据数组下标存即可。
for (int i = 0; i < nums2.length; i++) {
while (!stack.isEmpty() && nums2[stack.peek()] < nums2[i]) {
int pre = nums2[stack.pop()];
if (map.containsKey(pre)) {
res[map.get(pre)] = nums2[i];
}
}
stack.push(i);
}
return res;
503.下一个更大元素II
标签:栈 数组 单调栈 难度: 中等
给定一个循环数组 nums ( nums[nums.length - 1] 的下一个元素是 nums[0] ),返回 nums 中每个元素的 下一个更大元素 。
数字 x 的 下一个更大的元素 是按数组遍历顺序,这个数字之后的第一个比它更大的数,这意味着你应该循环地搜索它的下一个更大的数。如果不存在,则输出 -1 。
示例 1:
输入: nums = [1,2,1]
输出: [2,-1,2]
解释: 第一个 1 的下一个更大的数是 2;
数字 2 找不到下一个更大的数;
第二个 1 的下一个最大的数需要循环搜索,结果也是 2。
示例 2:
输入: nums = [1,2,3,4,3]
输出: [2,3,4,-1,4]
提示:
1 <= nums.length <= 104-109 <= nums[i] <= 109
一些基本信息读取:
下一个更大元素 单调栈了。然后如果不存在,则输出 -1 ,设置结果数组大小为原数组长度,初始化值为-1。然后这道题的特殊点就是循环数组。这一开始很容易就是想到,直接把原本数组再接在原始数组后面,这样就可以使用单调栈计算出每一个元素的下一个最大值。
原始想法实现:
int n = nums.length;
// 创建一个新的数组 ,大小为原始数组2倍
int[] doubledNums = new int[n * 2];
// 复制元素到新数组中
System.arraycopy(nums, 0, doubledNums, 0, n);
System.arraycopy(nums, 0, doubledNums, n, n);
// 初始化结果数组,大小为原数组长度,初始值为-1
int[] result = new int[n];
for (int i = 0; i < n; i++) {
result[i] = -1;
}
// 使用单调栈
Stack<Integer> stack = new Stack<>();
stack.push(0);
后续就是通用的,如果当前元素大于栈顶元素,则栈顶元素找到了下一个更大元素。
while (!stack.isEmpty() && doubledNums[i] > doubledNums[stack.peek()]) {
int index = stack.pop();
if (index < n) {
result[index] = doubledNums[i];
}
而后学习了下 代码随想录 的思想 : 扩充nums数组相当于多了一个O(n)的操作。其实也可以不扩充nums,而是在遍历的过程中模拟走了两边nums。
【取余】
public int[] nextGreaterElements(int[] nums) {
//边界判断
if (nums == null || nums.length <= 1) {
return new int[]{-1};
}
int size = nums.length;
int[] result = new int[size];//存放结果
Arrays.fill(result, -1);//默认全部初始化为-1
Stack<Integer> stack = new Stack<>();//栈中存放的是nums中的元素下标
// 等于走两边这个数组,用取余就知道当前的下标值具体原数组中的多少
for (int i = 0; i < 2 * size; i++) {
while (!stack.empty() && nums[i % size] > nums[stack.peek()]) {
result[stack.peek()] = nums[i % size];//更新result
stack.pop();//弹出栈顶
}
stack.push(i % size);
}
return result;
}