A. X Axis
You are given three points with integer coordinates x 1 x_1 x1, x 2 x_2 x2, and x 3 x_3 x3 on the X X X axis ( 1 ≤ x i ≤ 10 1 \leq x_i \leq 10 1≤xi≤10). You can choose any point with an integer coordinate a a a on the X X X axis. Note that the point a a a may coincide with x 1 x_1 x1, x 2 x_2 x2, or x 3 x_3 x3. Let f ( a ) f(a) f(a) be the total distance from the given points to the point a a a. Find the smallest value of f ( a ) f(a) f(a).
The distance between points a a a and b b b is equal to ∣ a − b ∣ |a - b| ∣a−b∣. For example, the distance between points a = 5 a = 5 a=5 and b = 2 b = 2 b=2 is 3 3 3.
Input
Each test consists of multiple test cases. The first line contains a single integer t t t ( 1 ≤ t ≤ 1 0 3 1 \leq t \leq 10^3 1≤t≤103) — the number of test cases. Then follows their descriptions.
The single line of each test case contains three integers x 1 x_1 x1, x 2 x_2 x2, and x 3 x_3 x3 ( 1 ≤ x i ≤ 10 1 \leq x_i \leq 10 1≤xi≤10) — the coordinates of the points.
Output
For each test case, output the smallest value of f ( a ) f(a) f(a).
Example
| i n p u t \tt input input |
|---|
| 8 1 1 1 1 5 9 8 2 8 10 9 3 2 1 1 2 4 1 7 3 5 1 9 4 |
| o u t p u t \tt output output |
| 0 8 6 7 1 3 4 8 |
Note
In the first test case, the smallest value of f ( a ) f(a) f(a) is achieved when a = 1 a = 1 a=1: f ( 1 ) = ∣ 1 − 1 ∣ + ∣ 1 − 1 ∣ + ∣ 1 − 1 ∣ = 0 f(1) = |1 - 1| + |1 - 1| + |1 - 1| = 0 f(1)=∣1−1∣+∣1−1∣+∣1−1∣=0.
In the second test case, the smallest value of f ( a ) f(a) f(a) is achieved when a = 5 a = 5 a=5: f ( 5 ) = ∣ 1 − 5 ∣ + ∣ 5 − 5 ∣ + ∣ 9 − 5 ∣ = 8 f(5) = |1 - 5| + |5 - 5| + |9 - 5| = 8 f(5)=∣1−5∣+∣5−5∣+∣9−5∣=8.
In the third test case, the smallest value of f ( a ) f(a) f(a) is achieved when a = 8 a = 8 a=8: f ( 8 ) = ∣ 8 − 8 ∣ + ∣ 2 − 8 ∣ + ∣ 8 − 8 ∣ = 6 f(8) = |8 - 8| + |2 - 8| + |8 - 8| = 6 f(8)=∣8−8∣+∣2−8∣+∣8−8∣=6.
In the fourth test case, the smallest value of f ( a ) f(a) f(a) is achieved when a = 9 a = 9 a=9: f ( 10 ) = ∣ 10 − 9 ∣ + ∣ 9 − 9 ∣ + ∣ 3 − 9 ∣ = 7 f(10) = |10 - 9| + |9 - 9| + |3 - 9| = 7 f(10)=∣10−9∣+∣9−9∣+∣3−9∣=7.
Tutorial
易得只要找到的点在其最大值和最小值中间即可
此解法时间复杂度为 O ( n ) \mathcal O(n) O(n),即找最大值和最小值的复杂度
Solution
for _ in range(int(input())):
a = list(map(int, input().split()))
print(max(a) - min(a))
B. Matrix Stabilization
You are given a matrix of size n × m n \times m n×m, where the rows are numbered from 1 1 1 to n n n from top to bottom, and the columns are numbered from 1 1 1 to m m m from left to right. The element at the intersection of the i i i-th row and the j j j-th column is denoted by a i j a_{ij} aij.
Consider the algorithm for stabilizing matrix a a a:
- Find the cell ( i , j ) (i, j) (i,j) such that its value is strictly greater than the values of all its neighboring cells. If there is no such cell, terminate the algorithm. If there are multiple such cells, choose the cell with the smallest value of i i i, and if there are still multiple cells, choose the one with the smallest value of j j j.
- Set a i j = a i j − 1 a_{ij} = a_{ij} - 1 aij=aij−1.
- Go to step 1 1 1.
In this problem, cells ( a , b ) (a, b) (a,b) and ( c , d ) (c, d) (c,d) are considered neighbors if they share a common side, i.e., ∣ a − c ∣ + ∣ b − d ∣ = 1 |a - c| + |b - d| = 1 ∣a−c∣+∣b−d∣=1.
Your task is to output the matrix a a a after the stabilization algorithm has been executed. It can be shown that this algorithm cannot run for an infinite number of iterations.
Input
Each test consists of multiple sets of input data. The first line contains a single integer t t t ( 1 ≤ t ≤ 1 0 4 1 \leq t \leq 10^4 1≤t≤104) — the number of sets of input data. This is followed by their description.
The first line of each set of input data contains two integers n n n and m m m ( 1 ≤ n , m ≤ 100 , n ⋅ m > 1 1 \leq n, m \leq 100, n \cdot m > 1 1≤n,m≤100,n⋅m>1) — the number of rows and columns of matrix a a a.
The next n n n lines describe the corresponding rows of the matrix. The i i i-th line contains m m m integers a i 1 , a i 2 , … , a i m a_{i1}, a_{i2}, \ldots, a_{im} ai1,ai2,…,aim ( 1 ≤ a i j ≤ 1 0 9 1 \leq a_{ij} \leq 10^9 1≤aij≤109).
It is guaranteed that the sum of n ⋅ m n \cdot m n⋅m over all sets of input data does not exceed 2 ⋅ 1 0 5 2 \cdot 10^5 2⋅105.
Output
For each set of input data, output n n n lines with m m m numbers in each line — the values of the cells of matrix a a a after the stabilization algorithm.
Example
| i n p u t \tt input input |
|---|
| 6 1 2 3 1 2 1 1 1 2 2 1 2 3 4 2 3 7 4 5 1 8 10 5 4 92 74 31 74 74 92 17 7 31 17 92 3 74 7 3 92 7 31 1 1 3 3 1000000000 1 1000000000 1 1000000000 1 1000000000 1 1000000000 |
| o u t p u t \tt output output |
| 1 1 1 1 1 2 3 3 4 4 5 1 8 8 74 74 31 31 74 74 17 7 31 17 17 3 31 7 3 3 7 7 1 1 1 1 1 1 1 1 1 1 1 |
Note
In the first set of input data, the algorithm will select the cell ( 1 , 1 ) (1, 1) (1,1) twice in a row and then terminate.

In the second set of input data, there is no cell whose value is strictly greater than the values of all neighboring cells.
In the third set of input data, the algorithm will select the cell ( 2 , 2 ) (2, 2) (2,2) and then terminate.

In the fourth set of input data, the algorithm will select the cell ( 1 , 1 ) (1, 1) (1,1) three times and then the cell ( 2 , 3 ) (2, 3) (2,3) twice.
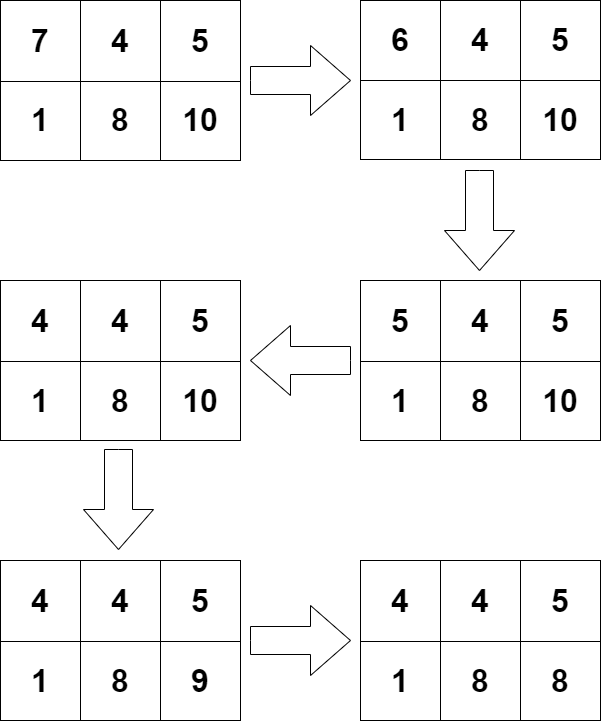
Tutorial
可以一次一次遍历所有元素,根据规则,如果有元素被更改,则进行下一次遍历,如果遍历一次根据都没有更改元素,那么说明矩阵都不能再改变了,即得到答案
此解法时间复杂度为 O ( n m ) \mathcal O(nm) O(nm)
Solution
dx = [0, 0, 1, -1]
dy = [1, -1, 0, 0]
def ok(x, y, n, m):
return 0 <= x < n and 0 <= y < m
for _ in range(int(input())):
n, m = map(int, input().split())
g = [list(map(int, input().split())) for _ in range(n)]
for i in range(n):
for j in range(m):
mx = 0
for k in range(4):
x, y = i + dx[k], j + dy[k]
if ok(x, y, n, m):
mx = max(mx, g[x][y])
g[i][j] = min(g[i][j], mx)
for gi in g:
print(*gi)
C. Update Queries
Let’s consider the following simple problem. You are given a string s s s of length n n n, consisting of lowercase Latin letters, as well as an array of indices i n d ind ind of length m m m ( 1 ≤ i n d i ≤ n 1 \leq ind_i \leq n 1≤indi≤n) and a string c c c of length m m m, consisting of lowercase Latin letters. Then, in order, you perform the update operations, namely, during the i i i-th operation, you set s i n d i = c i s_{ind_i} = c_i sindi=ci. Note that you perform all m m m operations from the first to the last.
Of course, if you change the order of indices in the array i n d ind ind and/or the order of letters in the string c c c, you can get different results. Find the lexicographically smallest string s s s that can be obtained after m m m update operations, if you can rearrange the indices in the array i n d ind ind and the letters in the string c c c as you like.
A string a a a is lexicographically less than a string b b b if and only if one of the following conditions is met:
- a a a is a prefix of b b b, but a ≠ b a \neq b a=b;
- in the first position where a a a and b b b differ, the symbol in string a a a is earlier in the alphabet than the corresponding symbol in string b b b.
Input
Each test consists of several sets of input data. The first line contains a single integer t t t ( 1 ≤ t ≤ 1 0 4 1 \leq t \leq 10^4 1≤t≤104) — the number of sets of input data. Then follows their description.
The first line of each set of input data contains two integers n n n and m m m ( 1 ≤ n , m ≤ 1 0 5 1 \leq n, m \leq 10^5 1≤n,m≤105) — the length of the string s s s and the number of updates.
The second line of each set of input data contains a string s s s of length n n n, consisting of lowercase Latin letters.
The third line of each set of input data contains m m m integers i n d 1 , i n d 2 , … , i n d m ind_1, ind_2, \ldots, ind_m ind1,ind2,…,indm ( 1 ≤ i n d i ≤ n 1 \leq ind_i \leq n 1≤indi≤n) — the array of indices i n d ind ind.
The fourth line of each set of input data contains a string c c c of length m m m, consisting of lowercase Latin letters.
It is guaranteed that the sum of n n n over all sets of input data does not exceed 2 ⋅ 1 0 5 2 \cdot 10^5 2⋅105. Similarly, the sum of m m m over all sets of input data does not exceed 2 ⋅ 1 0 5 2 \cdot 10^5 2⋅105.
Output
For each set of input data, output the lexicographically smallest string s s s that can be obtained by rearranging the indices in the array i n d ind ind and the letters in the string c c c as you like.
Example
| i n p u t \tt input input |
|---|
| 4 1 2 a 1 1 cb 4 4 meow 1 2 1 4 zcwz 7 4 abacaba 1 3 5 7 damn 7 10 traktor 7 6 5 4 3 2 1 6 4 2 codeforces |
| o u t p u t \tt output output |
| b cwoz abdcmbn ccdeefo |
Note
In the first set of input data, you can leave the array i n d ind ind and the string c c c unchanged and simply perform all operations in that order.
In the second set of input data, you can set the array i n d = [ 1 , 1 , 4 , 2 ] ind = [1, 1, 4, 2] ind=[1,1,4,2] and c = c = c= “zczw”. Then the string s s s will change as follows: m e o w → z e o w → c e o w → c e o z → c w o z meow \rightarrow zeow \rightarrow ceow \rightarrow ceoz \rightarrow cwoz meow→zeow→ceow→ceoz→cwoz.
In the third set of input data, you can leave the array i n d ind ind unchanged and set $c = $ “admn”. Then the string s s s will change as follows: a b a c a b a → a b a c a b a → a b d c a b a → a b d c m b a → a b d c m b n abacaba \rightarrow abacaba \rightarrow abdcaba \rightarrow abdcmba \rightarrow abdcmbn abacaba→abacaba→abdcaba→abdcmba→abdcmbn.
Tutorial
由于只有最后一次修改会改变每个位置的值,所以只需要将每个靠前的位置的元素变为更小的字符即可
所以可以贪心地对所有可以更改的字符排序,将每个修改过的位置贪心选择更小的字符即可
此解法时间复杂度为 O ( n log n ) \mathcal O(n \log n) O(nlogn)
Solution
for _ in range(int(input())):
n, m = map(int, input().split())
s = list(input())
a = sorted(set(list(map(int, input().split()))))
c = sorted(list(input()))
idx = 0
for ai in a:
s[ai - 1] = c[idx]
idx += 1
print(''.join(s))
D. Mathematical Problem
You are given a string s s s of length n > 1 n \gt 1 n>1, consisting of digits from 0 0 0 to 9 9 9. You must insert exactly n − 2 n - 2 n−2 symbols + + + (addition) or × \times × (multiplication) into this string to form a valid arithmetic expression.
In this problem, the symbols cannot be placed before the first or after the last character of the string s s s, and two symbols cannot be written consecutively. Also, note that the order of the digits in the string cannot be changed. Let’s consider s = 987009 s = 987009 s=987009:
- From this string, the following arithmetic expressions can be obtained: 9 × 8 + 70 × 0 + 9 = 81 9 \times 8 + 70 \times 0 + 9 = 81 9×8+70×0+9=81, 98 × 7 × 0 + 0 × 9 = 0 98 \times 7 \times 0 + 0 \times 9 = 0 98×7×0+0×9=0, 9 + 8 + 7 + 0 + 09 = 9 + 8 + 7 + 0 + 9 = 33 9 + 8 + 7 + 0 + 09 = 9 + 8 + 7 + 0 + 9 = 33 9+8+7+0+09=9+8+7+0+9=33. Note that the number 09 09 09 is considered valid and is simply transformed into 9 9 9.
- From this string, the following arithmetic expressions cannot be obtained: + 9 × 8 × 70 + 09 +9 \times 8 \times 70 + 09 +9×8×70+09 (symbols should only be placed between digits), 98 × 70 + 0 + 9 98 \times 70 + 0 + 9 98×70+0+9 (since there are 6 6 6 digits, there must be exactly 4 4 4 symbols).
The result of the arithmetic expression is calculated according to the rules of mathematics — first all multiplication operations are performed, then addition. You need to find the minimum result that can be obtained by inserting exactly n − 2 n - 2 n−2 addition or multiplication symbols into the given string s s s.
Input
Each test consists of multiple test cases. The first line contains a single integer t t t ( 1 ≤ t ≤ 1 0 4 1 \leq t \leq 10^4 1≤t≤104) — the number of test cases. Then follows their description.
The first line of each test case contains a single integer n n n ( 2 ≤ n ≤ 20 2 \leq n \leq 20 2≤n≤20) — the length of the string s s s.
The second line of each test case contains a string s s s of length n n n, consisting of digits from 0 0 0 to 9 9 9.
Output
For each test case, output the minimum result of the arithmetic expression that can be obtained by inserting exactly n − 2 n - 2 n−2 addition or multiplication symbols into the given string.
Example
| i n p u t \tt input input |
|---|
| 18 2 10 2 74 2 00 2 01 3 901 3 101 5 23311 6 987009 7 1111111 20 99999999999999999999 20 00000000000000000000 4 0212 18 057235283621345395 4 1112 20 19811678487321784121 4 1121 4 2221 3 011 |
| o u t p u t \tt output output |
| 10 74 0 1 9 1 19 0 11 261 0 0 0 12 93 12 24 0 |
Note
In the first four test cases, we cannot add symbols, so the answer will be the original number.
In the fifth test case, the optimal answer looks as follows: 9 × 01 = 9 × 1 = 9 9 \times 01 = 9 \times 1 = 9 9×01=9×1=9.
In the sixth test case, the optimal answer looks as follows: 1 × 01 = 1 × 1 = 1 1 \times 01 = 1 \times 1 = 1 1×01=1×1=1.
In the seventh test case, the optimal answer looks as follows: 2 + 3 + 3 + 11 = 19 2 + 3 + 3 + 11 = 19 2+3+3+11=19.
In the eighth test case, one of the optimal answers looks as follows: 98 × 7 × 0 + 0 × 9 = 0 98 \times 7 \times 0 + 0 \times 9 = 0 98×7×0+0×9=0.
Tutorial
由于需要刚好插入 n − 2 n - 2 n−2 个符号,所以其中被运算的若干数字中,有且仅有一个数字是两位数,其余数字均为个位数,所以可以枚举这个两位数,其余均为一位数
然后对这些数字进行计算,如果其中有 0,那么就可以乘以 0,最终答案即为
0
0
0,如果遇到 1,则直接乘以 1,此时数字不变,如果遇到的数字大于 1,那么直接加上这个数即可(如果乘以这个数那么必定比加上这个数大)
此解法时间复杂度为 O ( n 2 ) \mathcal O(n ^ 2) O(n2)
Solution
def f(a):
if a.count(0):
return 0
cnt = 0
for ai in a:
if ai > 1:
cnt += ai
return max(cnt, 1)
for _ in range(int(input())):
n = int(input())
s = list(input())
ans = 270
for i in range(n - 1):
a = []
for j in range(n):
if i == j:
a.append(int(s[j] + s[j + 1]))
elif j != i + 1:
a.append(int(s[j]))
ans = min(ans, f(a))
print(ans)