【算法】二叉树 - 理论基础

news2024/12/24 8:24:12

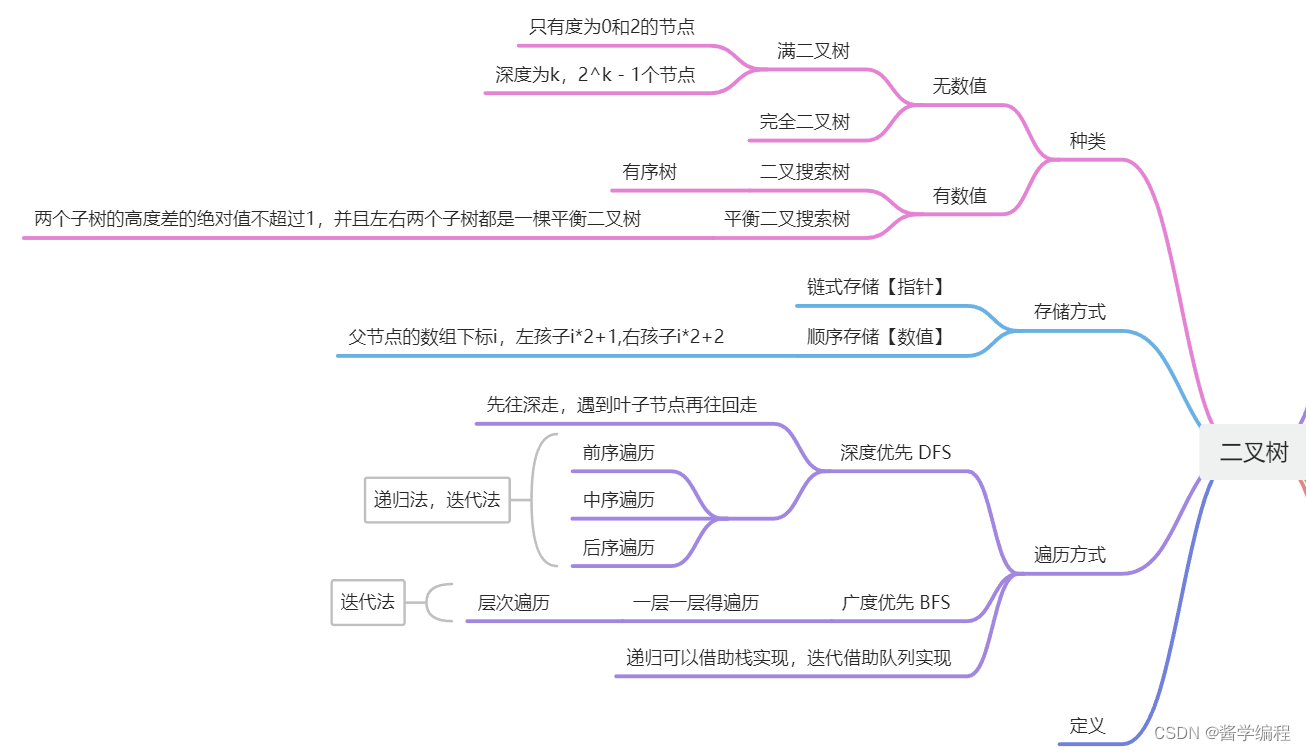
在这里插入图片描述

1.种类

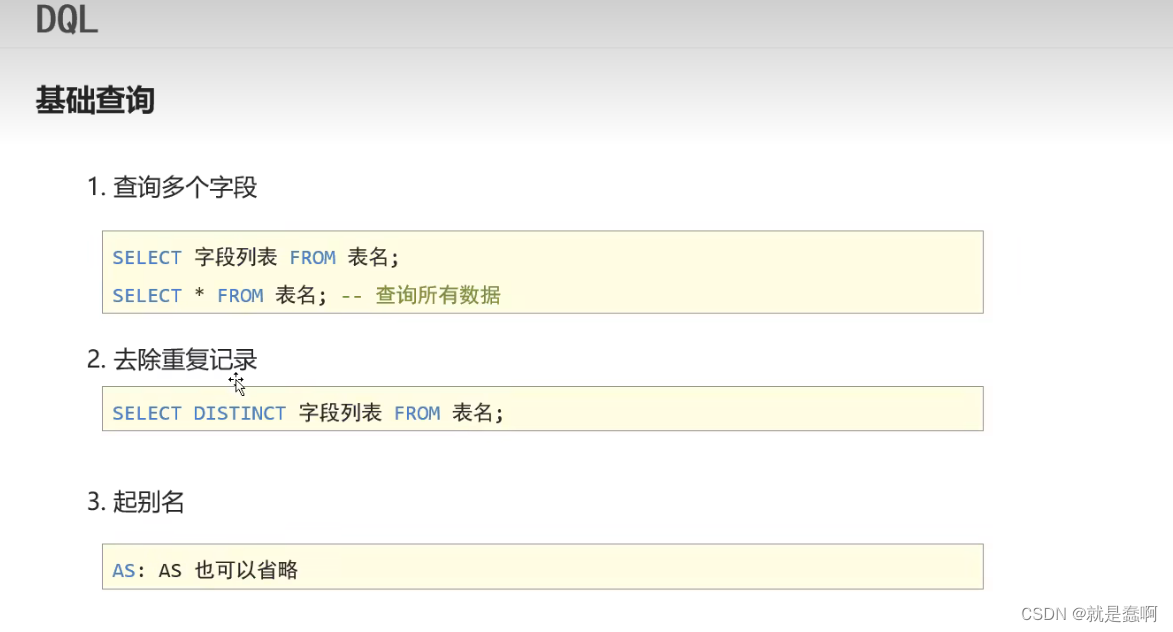
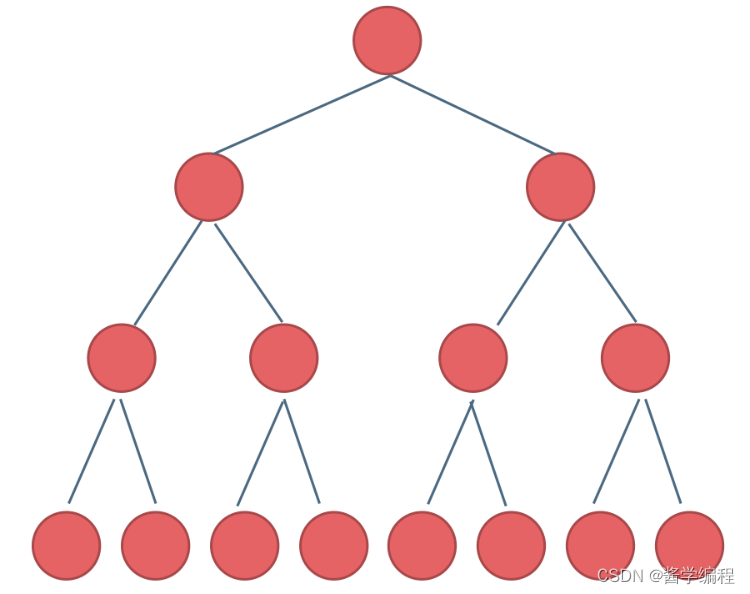
1.1 满二叉树

只有度为0和2的节点，且度为0的节点都都在同一层。深度为k，有2^k-1个节点。
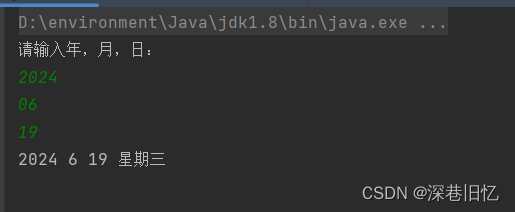
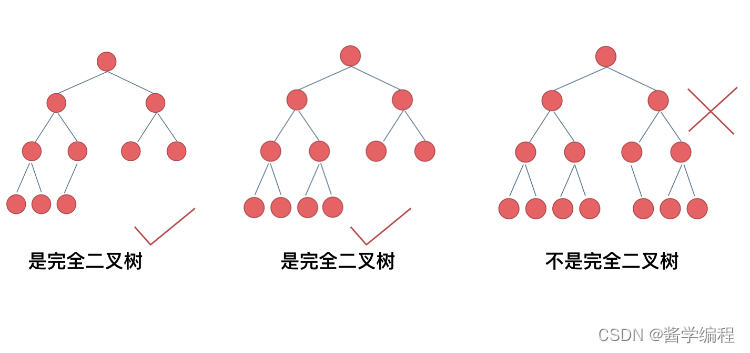
在这里插入图片描述

1.2 完全二叉树

在完全二叉树中，除了最底层节点可能没填满外，其余每层节点数都达到最大值，并且最下面一层的节点都集中在该层最左边的若干位置。若最底层为第 h 层（h从1开始），则该层包含 1~ 2^(h-1) 个节点。
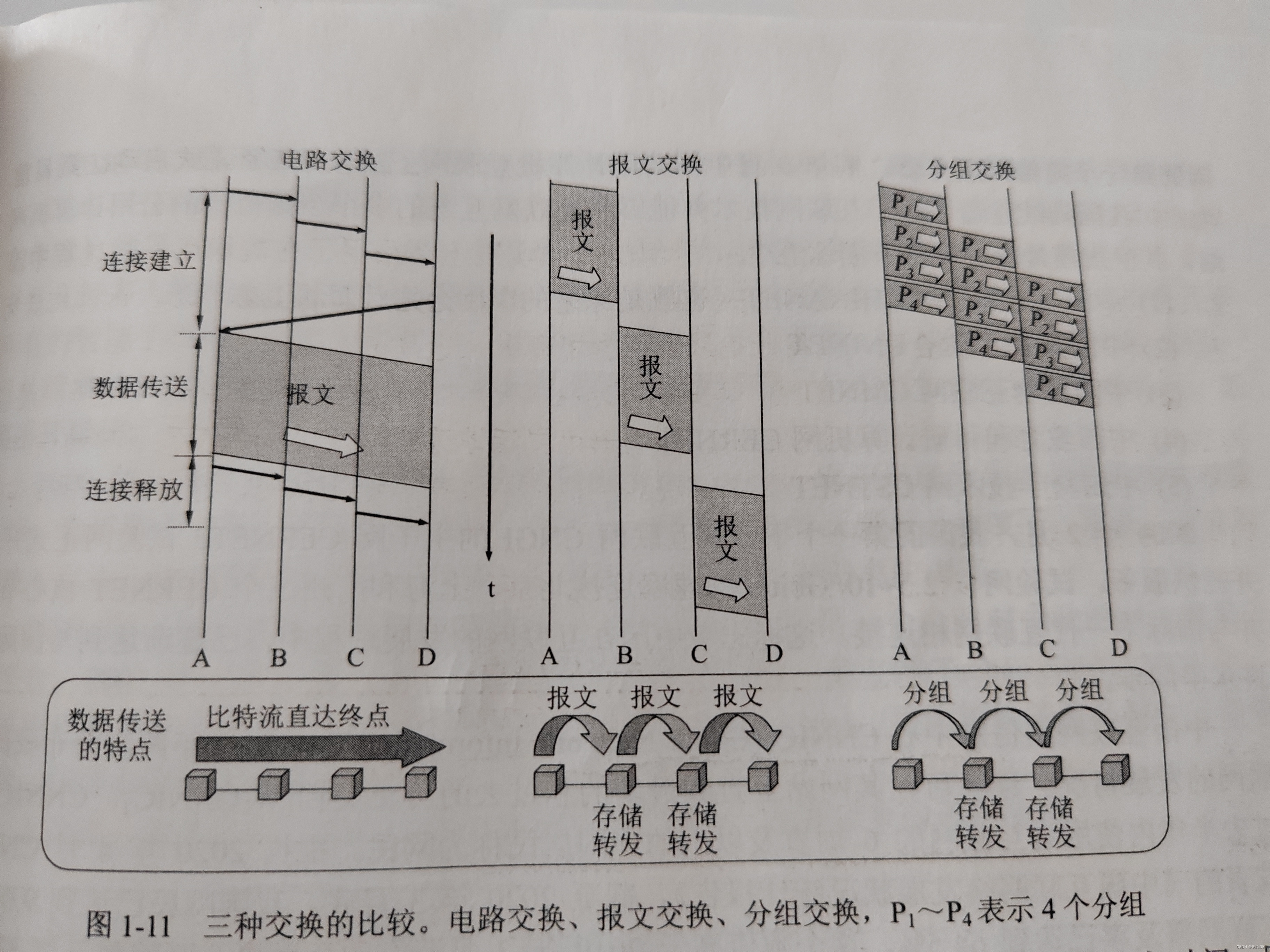
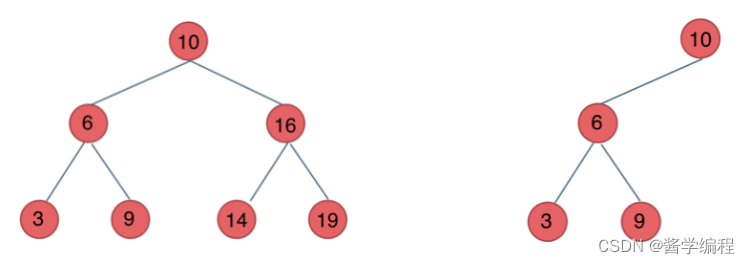
在这里插入图片描述

1.2 二叉树搜索树

有数值的有序树

若它的左子树不空，则左子树上所有结点的值均小于它的根结点的值；
若它的右子树不空，则右子树上所有结点的值均大于它的根结点的值；
它的左、右子树也分别为二叉排序树

在这里插入图片描述

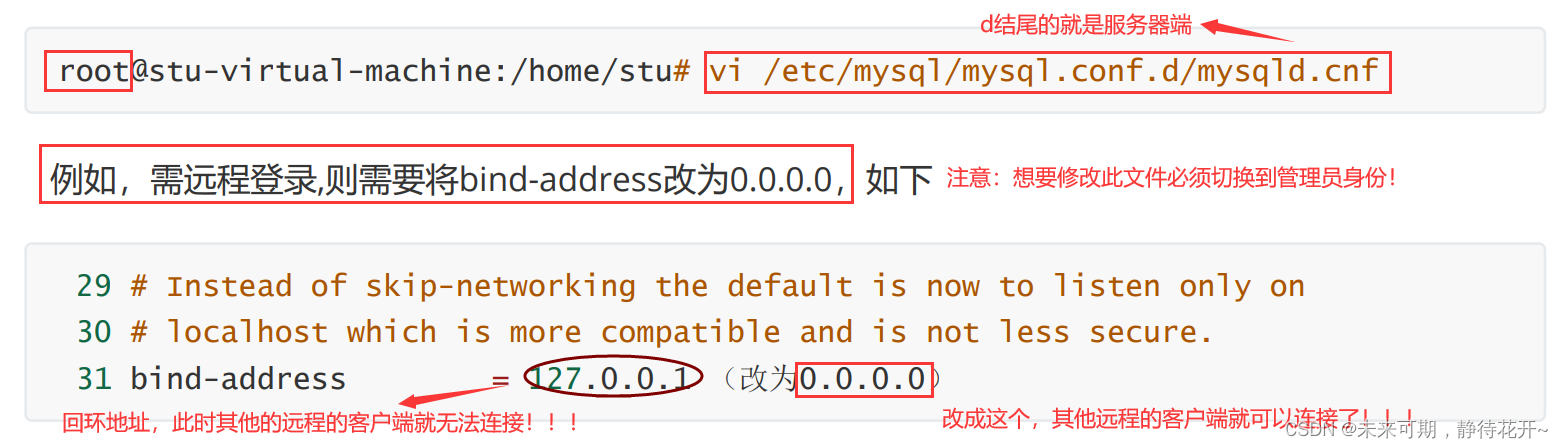
1.2 平衡二叉树搜索树 AVL（Adelson-Velsky and Landis）

它是一棵空树或它的左右两个子树的高度差的绝对值不超过1，并且左右两个子树都是一棵平衡二叉树。
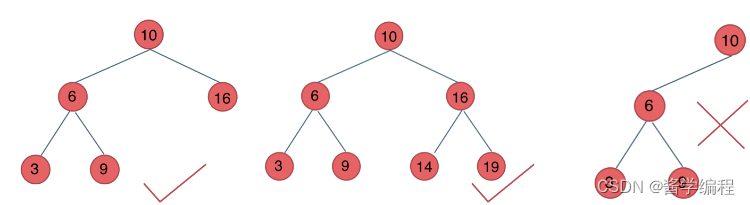
在这里插入图片描述
扩展：

AVL树和红黑树都是自平衡的二叉搜索树，它们都用于保持数据的有序性和平衡性，以便进行高效的搜索、插入和删除操作。尽管如此，它们之间存在一些关键的区别：

平衡要求：

AVL树是严格平衡的，要求任一节点的两个子树的高度差至多为1。这种严格的平衡使得AVL树的高度总是最小的，但这也意味着每次插入或删除操作后，可能需要更多的旋转来重新平衡树。
红黑树则是一种半平衡树，它通过特定的颜色标记（红色或黑色）和规则来维持树的近似平衡，而不追求严格的平衡。这导致红黑树可能比AVL树稍高一些，但在插入和删除操作中需要的旋转次数较少，因此整体性能更优。
性能差异：

在插入和删除操作中，红黑树通常表现得更好，因为它需要的旋转次数少于AVL树，尤其是在频繁的插入和删除操作中。
AVL树在查找操作方面可能略微优于红黑树，因为其严格的平衡性导致树的高度更小。适用场景：

如果搜索操作远多于插入和删除操作，AVL树可能是更好的选择。如果插入、删除和搜索操作频率相近，红黑树通常是一个更全面的选择。
Java的java.util.TreeMap和java.util.TreeSet选择使用红黑树作为底层数据结构的原因主要在于红黑树在一般情况下的平均性能表现。由于红黑树在插入和删除操作中的性能优势，它更适合于需要动态调整大小的数据结构。在实践中，红黑树的这些优点通常超过了AVL树在查找操作上的微小优势，特别是在数据集经常发生变化的情况下。

此外，红黑树的实现通常比AVL树更简单，这是因为红黑树的平衡规则较为直观，而且在插入和删除过程中涉及的旋转和重新平衡步骤也相对较少。这简化了代码的编写和维护，也是TreeMap和TreeSet选择红黑树的一个因素。

2.存储方式

2.1 链式存储

使用指针
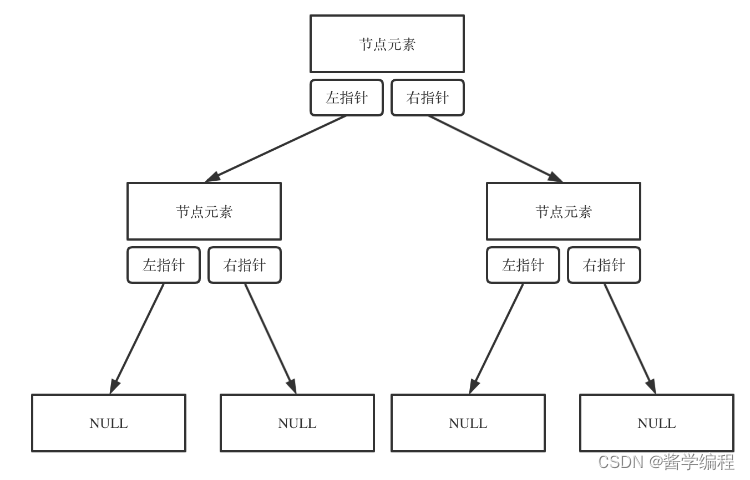
在这里插入图片描述

2.1 顺序存储

使用数组
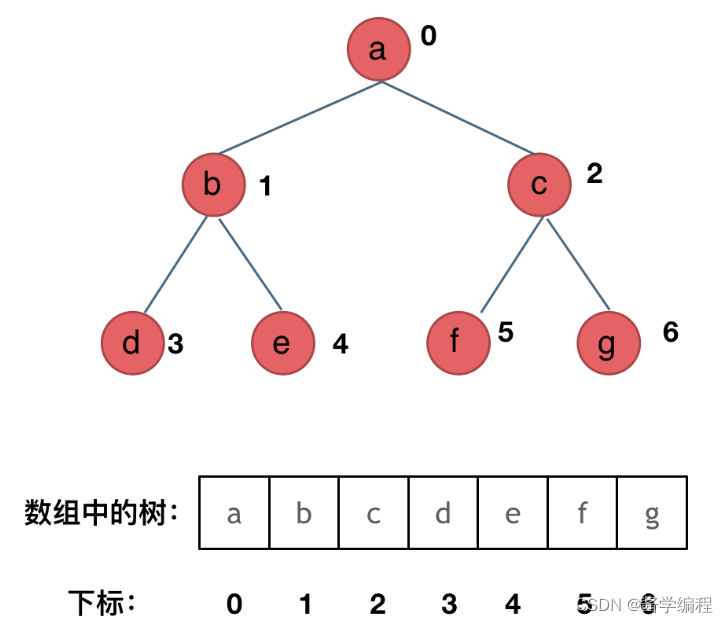
在这里插入图片描述
如果父节点的数组下标是 i，那么它的左孩子就是 i * 2 + 1，右孩子就是 i * 2 + 2。

一般使用链式存储二叉树，更易于理解。

3.遍历方式

3.1 深度优先遍历 DFS

先往深走，遇到叶子节点再回走。

前序遍历（递归法，迭代法）
中序遍历（递归法，迭代法）
后序遍历（递归法，迭代法）

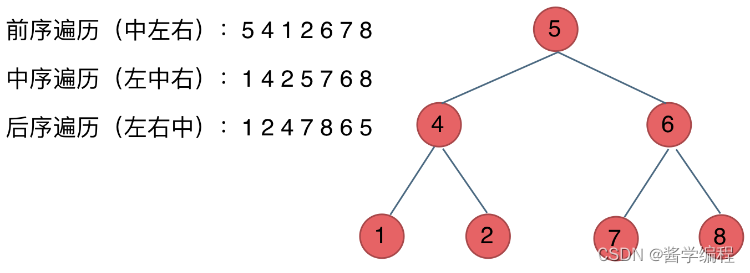
栈就是递归的一种实现结构。

3.2 广度优先遍历 BFS

一层一层遍历

层次遍历（迭代法）

使用队列作为辅助实现。

4.定义

public class TreeNode {
      int val;
      TreeNode left;
      TreeNode right;
      TreeNode() {}
      TreeNode(int val) { this.val = val; }
      TreeNode(int val, TreeNode left, TreeNode right) {
          this.val = val;
          this.left = left;
          this.right = right;
      }
  }
 /