适用平台:Matlab2021版及以上
数据清洗是数据处理和分析中的一个关键步骤,特别是对于像风电场这样的大型、复杂数据集。清洗数据的目的是为了确保数据的准确性、一致性和完整性,从而提高数据分析的质量和可信度,是深度学习训练和预测前的重要步骤。
-
在实际应用中,数据可能会因为传感器故障、通信错误或人为输入错误而产生异常值或噪声数据。这些异常值会严重影响后续的数据分析和模型训练。清洗数据可以确保数据的准确性,减少噪声对分析结果的干扰。
-
缺失值是数据集中常见的问题。如果不处理缺失值,可能会导致分析结果不准确或模型训练失败。通过填补缺失值,可以提高数据的完整性,确保每个数据点都有意义。
手动填充空值、删除异常值的方法需要耗费大量的时间,且准确性得不到保障,本程序以风电场数据为例,进行数据清洗和处理,包括异常值处理、缺失值处理、离群值处理、以及相关性分析,并将清洗后的数据保存到新的Excel文件中。
①异常值处理:
研究现状:
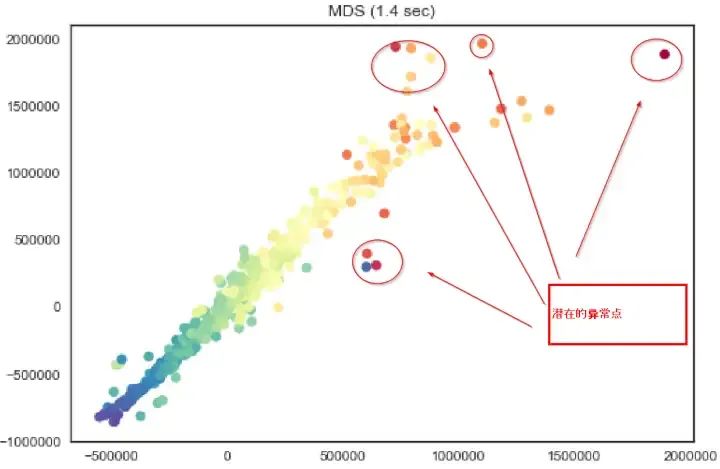
异常值检测与处理是数据预处理中的重要环节。常见方法包括统计方法(如Z-score、IQR)、机器学习方法(如支持向量机)、以及深度学习方法(如自编码器)。统计方法利用数据的统计特性(如均值、方差、中位数)进行异常值检测,适用于简单数据集。
本文方法:
-
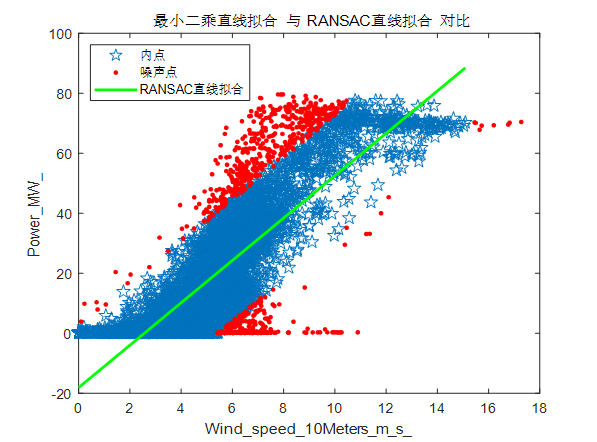
结合统计方法(删除全相同元素行)和基于RANSAC的鲁棒拟合方法,有效处理不同类型的异常值。
-
RANSAC方法能够在噪声和异常值存在的情况下进行可靠的模型拟合,适用于存在显著异常值的数据集。
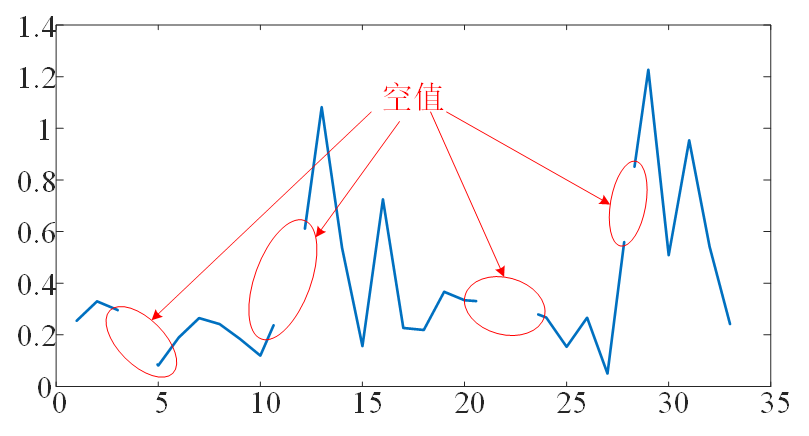
②缺失值处理
研究现状:
①缺失值处理方法多种多样,包括删除法、填补法(如均值填补、中位数填补、最近邻填补)、插值法(如线性插值、样条插值)、以及模型预测法(如多重插补、矩阵分解)。
②简单填补方法(如均值填补)易于实现,但可能引入偏差。
③插值法利用数据的连续性进行填补,适用于时间序列数据。
④模型预测法利用机器学习模型对缺失值进行预测,精度高,但计算复杂。
本文方法:
-
使用前向填补法简单有效,适用于时间序列数据,能够保留数据的趋势和模式。
-
前向填补法计算成本低,适合于大规模数据集的快速处理。
③离群值处理
研究现状:
①离群值检测方法包括基于统计的检测方法(如Grubbs' Test、Tukey's Fences)、基于聚类的方法(如K-means、DBSCAN)、基于机器学习的方法(如孤立森林、LOF)。
②统计方法适用于简单数据集,易于实现。
③聚类方法通过分析数据点的密度或距离来识别离群值,适用于聚类明显的数据集。
④机器学习方法能够处理复杂数据分布和高维数据,具有较高的检测准确性。
本文方法:
-
结合移动窗口统计特性(滑动窗线性插值)和基于残差的离群值检测方法(孤立森林),处理离群值的鲁棒性强。
-
使用中位数绝对离差(MAD)方法进行滑动窗线性插值,能够平滑数据波动,适用于时间序列数据。
-
残差分析结合孤立森林,能够有效识别复杂数据分布中的离群值。
④ 创新点总结
-
多方法结合,处理全面:
-
本程序结合了统计方法、拟合方法、插值方法和机器学习方法,能够全面、有效地处理异常值、缺失值和离群值。
-
通过删除全相同元素行、前向填补缺失值、滑动窗线性插值和RANSAC拟合等多种方法,保证数据处理的全面性和鲁棒性。
-
-
高效计算,适用性广:
-
采用简单有效的前向填补和滑动窗线性插值方法,计算成本低,适用于大规模数据集的快速处理。
-
RANSAC拟合和孤立森林方法适用于复杂数据分布,能够处理高维数据和噪声数据。
-
-
可视化展示,直观评估:
-
通过绘制处理前后的相关性热力图和特征对比图,直观展示数据处理效果,便于评估和验证处理方法的有效性。
-
可视化展示有助于理解数据特征和变化,增强数据处理的透明度和解释性。
-
程序结果
各特征变量清洗前后的数据对比:
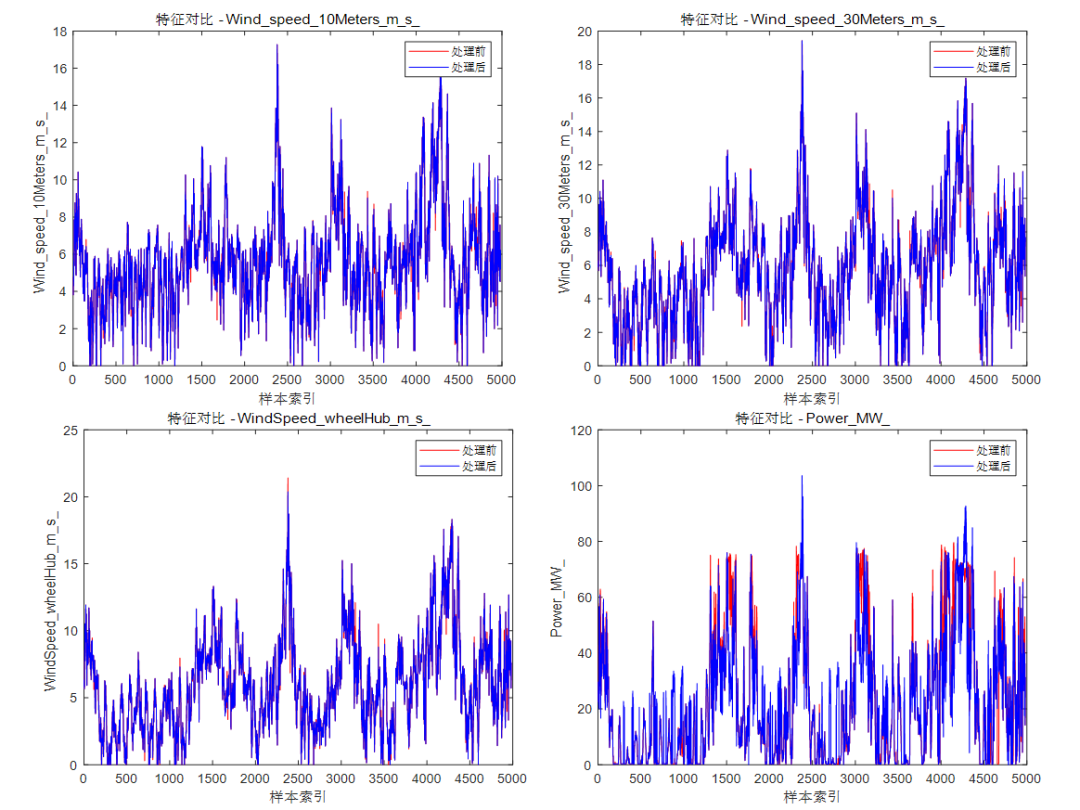

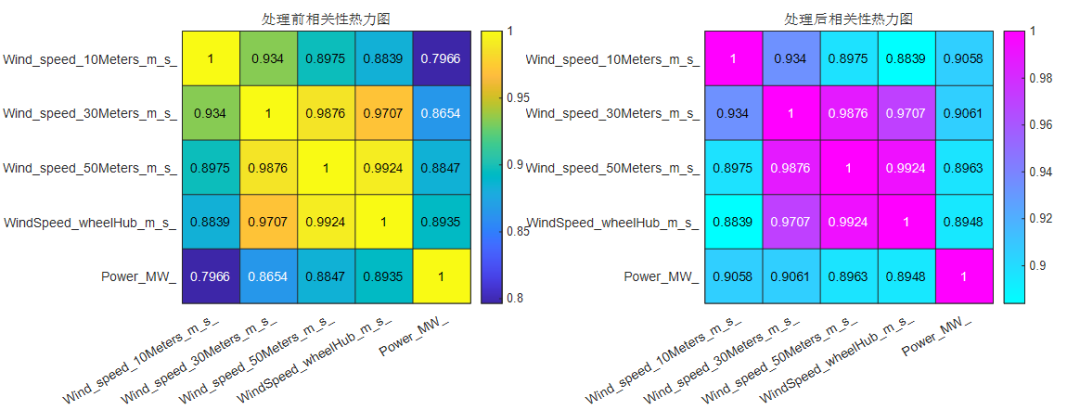
部分程序
%% 相关性极差的也定义为异常值
% 处理:采用Ransac拟合后替代 公众号:《创新优化及预测代码》
x = res_new(:, 1); % 提取第1列数据作为自变量
y = res_new(:, end); % 提取最后一列数据作为因变量
xyPoints = [x y]; % 组合自变量和因变量
% RANSAC直线拟合
sampleSize = 30; % 每次采样的点数
maxDistance = 400; % 内点到模型的最大距离
fitLineFcn = @(xyPoints) polyfit(xyPoints(:, 1), xyPoints(:, 2), 1); % 拟合函数,采用polyfit进行线性拟合
evalLineFcn = @(model, xyPoints) sum((y - polyval(model, x)).^2, 2); % 距离估算函数,计算点到拟合线的距离
[modelRANSAC, inlierIdx] = ransac(xyPoints, fitLineFcn, evalLineFcn, sampleSize, maxDistance); % 使用RANSAC算法拟合直线,并提取内点的索引
modelInliers = polyfit(xyPoints(inlierIdx, 1), xyPoints(inlierIdx, 2), 1); % 对内点进行最小二乘法线性拟合
figure;
plot(xyPoints(inlierIdx, 1), xyPoints(inlierIdx, 2), 'p',MarkerSize=10); % 绘制内点
hold on;
plot(xyPoints(~inlierIdx, 1), xyPoints(~inlierIdx, 2), 'r.',MarkerSize=10); % 绘制外点
hold on;
inlierPts = xyPoints(inlierIdx, :); % 提取内点数据
x2 = linspace(min(inlierPts(:, 1)), max(inlierPts(:, 1))); % 生成内点自变量范围的等间距点
y2 = polyval(modelInliers, x2); % 计算内点拟合直线上的值
plot(x2, y2, 'g-',LineWidth=2); % 绘制RANSAC直线拟合结果
hold off;
title('最小二乘直线拟合 与 RANSAC直线拟合 对比'); % 设置图标题
xlabel(variableNames{1}); % 设置X轴标签
ylabel(variableNames{end}); % 设置Y轴标签
legend('内点', '噪声点', 'RANSAC直线拟合', 'Location', 'NorthWest'); % 添加图例 % 公众号:《创新优化及预测代码》
%% 残差-孤立森林 公众号:《创新优化及预测代码》
% 计算Ransac理论值
T_linear = (modelRANSAC(1) * res_new(:, 1) + modelRANSAC(2)); % 计算RANSAC理论直线值
for i = 1:size(T_linear, 1)
if T_linear(i, end) < 0
T_linear(i, end) = 0; % 将理论值小于0的部分设为0
end
end
residual_power = abs(res_new(:, end) - T_linear); % 计算实际值与理论值的残差
% 孤立森林判断异常值
[error_pos2] = iso_forest([res_new(:, :) residual_power]); % 使用孤立森林算法检测异常值 % 公众号:《创新优化及预测代码》
%% 替代异常值
for i = 1:size(error_pos2, 2)
res_new(error_pos2{i, 1}, end) = T_linear(error_pos2{i, 1}); % 将检测出的异常值替换为理论值
end
res_new(~inlierIdx, end) = T_linear(~inlierIdx); % 将RANSAC检测出的异常值也替换为理论值部分内容源自网络,侵权联系删除!
欢迎感兴趣的小伙伴关注并私信获取完整版代码,小编会不定期更新高质量的学习资料、文章和程序代码,为您的科研加油助力!