目录
What is Non-Parametric About?
What is Non-Parametric About?
在我们继续之前，我只想强调一个常见的误解。当我们考虑使用非参数 Double-ML 模型来估计 CATE 时，我们似乎会得到一个非线性治疗效果。例如，让我们假设一个非常简单的数据生成过程（DGP），其中 discont 对销售额的影响是非线性的，但却是通过平方根函数产生的。
治疗效果由该销售函数相对于治疗的导数给出。
我们可以看到，治疗效果不是线性的。实际上，治疗效果会随着治疗次数的增加而减弱。这对 DGP 有很大的意义。起初，一点点折扣会使销售额大幅增加。但是，当我们给予的折扣太多时，多一个单位的折扣对销售额的影响就会越来越小，因为人们不会想买到无穷多。因此，折扣只在人们满足之前有效。
那么问题来了，非参数 ML 能否捕捉到治疗效果中的这种饱和行为？它能否从较小的折扣水平推断出，如果折扣更高，治疗效果会更低？答案是......可以这么说。为了更好地理解这一点，让我们生成类似上述 DGP 的数据。
np.random.seed(321)
n=5000
discount = np.random.gamma(2,10, n).reshape(-1,1)
discount.sort(axis=0) # for better ploting
sales = np.random.normal(20+10*np.sqrt(discount), 1)如果我们绘制这个 DGP，就可以看到这些变量之间的平方根关系。
plt.plot(discount, 20 + 10*np.sqrt(discount))
plt.ylabel("Sales")
plt.xlabel("Discount");
现在，让我们对这些数据应用非参数双重/偏差 ML。
debias_m = LGBMRegressor(max_depth=3)
denoise_m = LGBMRegressor(max_depth=3)
# orthogonalising step
discount_res = discount.ravel() - cross_val_predict(debias_m, np.ones(discount.shape), discount.ravel(), cv=5)
sales_res = sales.ravel() - cross_val_predict(denoise_m, np.ones(sales.shape), sales.ravel(), cv=5)
# final, non parametric causal model
non_param = LGBMRegressor(max_depth=3)
w = discount_res ** 2
y_star = sales_res / discount_res
non_param.fit(X=discount_res.reshape(-1,1), y=y_star.ravel(), sample_weight=w.ravel());通过上述模型，我们可以得到 CATE 估计值。这里的问题是 CATE 不是线性的。随着治疗次数的增加，CATE 应该减少。我们要回答的问题是，非参数模型能否捕捉到这种非线性。
要正确回答这个问题，让我们记住双重/偏差 ML 对数据生成过程的基本假设是什么。这些假设可以从我们之前列出的等式中看出。
也就是说，残差结果等于残差治疗乘以条件治疗效果。这意味着治疗对结果的影响是线性的。这里不存在非线性。上述模型表明, 如果我们将治疗从 1 增加到 10 或从 100 增加到 110, outcome将提高一个固定的 。这是一个简单的乘法。
那么，这是否意味着非参数模型无法捕捉治疗效果的非线性呢？也不尽然... 相反，Double/ML 找到了非线性 CATE 的局部线性近似值。换句话说，它找到的是在治疗水平上或治疗周围，结果相对于治疗的导数。这相当于找到与治疗点上的结果函数相切的线的斜率。
这意味着，是的，非参数双 ML 会发现随着治疗量的增加，治疗效果会变小。但是，不，它不会发现非线性治疗效果，而是局部线性治疗效果。我们甚至可以将这些线性近似值与地面真实的非线性因果效应进行对比，事实上，它们是很好的近似值。
cate = non_param.predict(X=discount)
plt.figure(figsize=(15,5))
plt.subplot(1,2,1)
plt.scatter(discount, sales)
plt.plot(discount, 20 + 10*np.sqrt(discount), label="Ground Truth", c="C1")
plt.title("Sales by Discount")
plt.xlabel("Discount")
plt.legend()
plt.subplot(1,2,2)
plt.scatter(discount, cate, label="$\hat{\\tau}(x)$", c="C4")
plt.plot(discount, 5/np.sqrt(discount), label="Ground Truth", c="C2")
plt.title("CATE ($\partial$Sales) by Discount")
plt.xlabel("Discount")
plt.legend();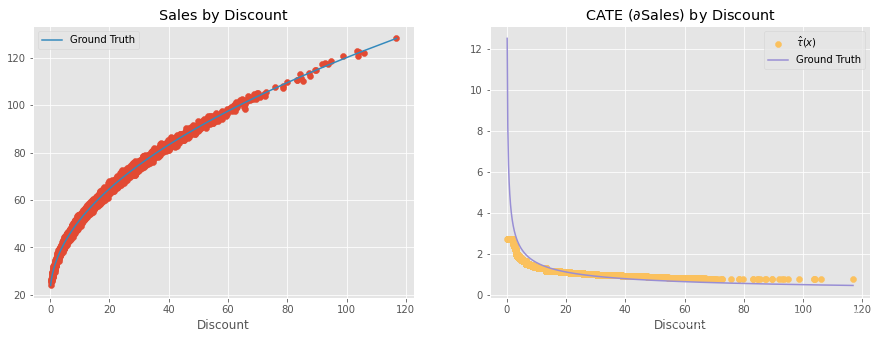
这听起来像是技术性问题，但却有非常实际的意义。例如，假设您在上面的例子中发现对某位顾客的处理效应为 2，这意味着如果您将折扣提高 1 个单位，您对该顾客的销售额就会增加 2 个单位。看到这个结果，你可能会想："太好了！我会给这个单位很多折扣！毕竟，每增加 1 个单位的折扣，我就能获得 2 个单位的销售额"。然而，这是错误的结论。只有在这个折扣水平上，治疗效果才是 2。只要提高折扣，效果就会下降。例如，假设这位顾客只获得了 5 折，所以她的治疗效果很高。如果你看到了这个巨大的治疗效果，并以此为理由给这位顾客 20 折。但是，当你这样做时，效果可能会从 2 降到 0.5 左右。在治疗效果为 2 时，打 20 折是合理的，但在治疗效果为 0.5 时，打 20 折就不再有利可图了。
这意味着，在将非线性治疗效果推断到新的治疗水平时，您必须格外小心。否则，你最终可能会做出非常无利可图的决定。另一种说法是，当治疗效果不是线性的时候，即使是非参数的双重/偏差-ML 也很难做出反事实结果预测。它会试图将治疗效果（TE）从低治疗水平线性推断到高治疗水平，或反过来推断。由于非线性，这种推断很可能会出现偏差。
为了解决这个问题，有一个最终的想法。请记住，与我们之前看到的方法相比，这个方法的科学性要低得多。它可以归结为在应用正交化程序后使用 S-学习器，但我说得太快了。让我们接下来看看。
