Leetcode 2713. 矩阵中严格递增的单元格数

DFS

容易想到，枚举每个点作为起点，向同行同列的可跳跃点dfs，维护全局变量记录可达的最远距离

超时，通过样例193 / 566

class Solution {
    int res = 0;
    
    public void dfs(int[][] mat, int x, int y, int step){
        step ++;
        res = Math.max(res, step);
        int n = mat.length;
        int m = mat[0].length;
        int num = mat[x][y];
        for(int i = 0; i < n; i ++){
            if(mat[i][y] > num){
                dfs(mat, i, y, step);
            }
        }
        for(int j = 0; j < m; j ++){
            if(mat[x][j] > num){
                dfs(mat, x, j, step);
            }
        }
        return;
    }

    public int maxIncreasingCells(int[][] mat) {
        int n = mat.length;
        int m = mat[0].length;
        for(int i = 0 ; i < n; i ++){
            for(int j = 0 ; j < m; j ++){
                dfs(mat, i, j, 0);
            }
        }
        return res;
    }
}

---

DFS+记忆化搜索

在DFS中注意到，存在很多重复计算，无论以哪个点作为起点，当跳跃到(x, y)点后，后续的最远距离是固定的，若在其他的起点中已经计算过这个数值，则记录下来直接取用

使用mem[ i ][ j ]记录坐标(i, j)位置所能跳跃的最大距离，在进入DFS后，若这个点已经计算过，即mem[ i ][ j ]非0，则直接取用。若没有计算过，则进行DFS，并在DFS结束后更新mem[ i ][ j ]

超时，通过样例558 / 566

class Solution {
    int mem[][];
    // dfs函数返回(x,y)坐标可达最远距离，包含自身，最少为1
    public int dfs(int[][] mat, int x, int y){
        if(mem[x][y] != 0){
            return mem[x][y];
        }
        int n = mat.length;
        int m = mat[0].length;
        int res = 1;
        int num = mat[x][y];
        for(int i = 0; i < n; i ++){
            if(mat[i][y] > num){
                int ans = dfs(mat, i, y);
                res = Math.max(res, ans + 1);
            }
        }
        for(int j = 0; j < m; j ++){
            if(mat[x][j] > num){
                int ans = dfs(mat, x, j);
                res = Math.max(res, ans + 1);
            }
        }
        mem[x][y] = res;
        return res;
    }

    public int maxIncreasingCells(int[][] mat) {
        int n = mat.length;
        int m = mat[0].length;
        mem = new int [n][m];
        int res = 0;
        for(int i = 0 ; i < n; i ++){
            for(int j = 0 ; j < m; j ++){
                res = Math.max(res, dfs(mat, i, j));
            }
        }
        return res;
    }
}

---

DP

经过优化无法使用DFS通过所有样例，重新分析问题

对于点(x, y)来说，以其作为起点，该点所能到达的最远距离，取决于该行和该列中其他点所能到达的最远距离，即为Max（行可达最远，列可达最远）+1

但移动规则为只能向更大的点进行移动，若每次移动前对行列所有元素都进行检查同样会造成时间浪费，因此将n*m个位置根据值进行降序排序，从大到小进行处理

这样带来的好处是，无需考虑跳跃规则问题，当处理一个元素时，已经记录的行可达最远的点是一定大于它的，一定可以向其移动

另一方面，只需求出移动的最远距离，因此无需记录一次移动使用哪个位置转移过来的，只需要知道此次移动的距离是多少就可以，即第 i 行的行可达最远只需要O(1)的空间，来实时维护此时该行已经处理过的最远距离，列同理

由此构思所需要的空间
dp[ i ][ j ] 记录(i, j)位置为起点，所能移动的最远距离
rowMax[ i ] 记录第 i 行此时已经存在的最远距离，即该行中存在一个点，该点为起点所能移动的距离最远为rowMax[ i ]，初始化为0
colMax[ j ] 记录第 j 列此时已经存在的最远距离，即该列中存在一个点，该点为起点所能移动的距离最远为colMax[ i ]，初始化为0
则dp[ i ][ j ] = Max{ rowMax[ i ], colMax[ j ] } + 1
计算后更新rowMax[ i ] 和 colMax[ j ]

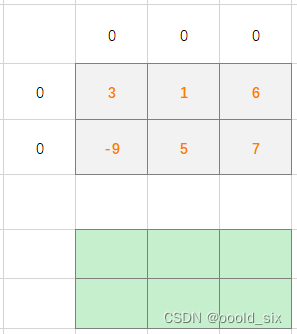
起点7：dp = max(0, 0) + 1 = 1，更新rowMax[ 1 ] = 1，更新colMax[ 2 ] = 1
起点6：dp = max(0, 1) + 1 = 2，更新rowMax[ 0 ] = 2，更新colMax[ 2 ] = 2
起点5：dp = max(1, 0) + 1 = 2，更新rowMax[ 1 ] = 2，更新colMax[ 1 ] = 2
起点3：dp = max(2, 0) + 1 = 3，更新rowMax[ 0 ] = 3，更新colMax[ 0 ] = 3
起点1：dp = max(3, 2) + 1 = 4，更新rowMax[ 0 ] = 4，更新colMax[ 1 ] = 4
起点-9：dp = max(2, 3) + 1 = 4，更新rowMax[ 1 ] = 4，更新colMax[ 0 ] = 4

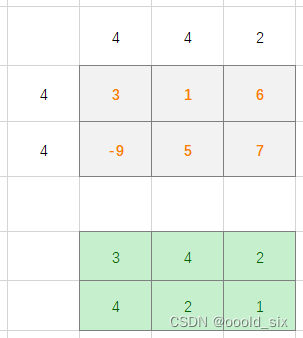
另外注意，存在相同元素，此时计算dp时不应更新rowMax，违背了rowMax的定义“该行内存在一点，以其为起点所答的最远距离为rowMax[ i ]，dp[ i ] [ j ] = rowMax + 1”，因为对于同样的元素来说，他们之间是不可达的，因此对于相同元素来说，此时更新rowMax会导致从值k移动到值k 的情况发生

因此将相同元素作为一批同时处理，其间使用rowMax计算dp，而定义一个新数组rowTemp来临时记录rowMax应有的变化，当这一批值相同的元素dp计算结束后，再将rowTemp赋值给rowMax以用于后续的计算，colMax同理

class Solution {
	// Pair类记录一个点的值和坐标，用于排序
    public class Pair{
        private int val;
        private int x;
        private int y;

        public Pair(int val, int x, int y) {
            this.val = val;
            this.x = x;
            this.y = y;
        }
    }

    public int maxIncreasingCells(int[][] mat) {
        int n = mat.length;
        int m = mat[0].length;
        Pair pairs[] = new Pair[n * m];
        int index = 0;
        for(int i = 0 ; i < n; i ++){
            for(int j = 0; j < m; j ++){
                pairs[index++] = new Pair(mat[i][j], i, j);
            }
        }
		// 降序排序所有点
        Arrays.sort(pairs, (p1, p2) -> Integer.compare(p2.val, p1.val));
        int rowMax[] = new int [n];
        int colMax[] = new int [m];
        int dp[][] = new int [n][m];
        int res = 0;
        for(int i = 0 ; i < n*m; i ++){
            int val = pairs[i].val;
            int x = pairs[i].x;
            int y = pairs[i].y;
            // 相同元素情况
            if(i+1 < n*m && pairs[i+1].val == val){
                int l = i;
                int r = i + 1;
                // 确定范围
                while(r < n*m && pairs[r].val == val)
                    r ++;
                // rowMax副本
                int rowTemp[] = rowMax.clone();
                int colTemp[] = colMax.clone();
                // 统一处理计算dp
                for(int k = l; k < r; k ++){
                    int kx = pairs[k].x;
                    int ky = pairs[k].y;
                    int kval = pairs[k].val;
                    dp[kx][ky] = Math.max(rowMax[kx], colMax[ky]) + 1;
                    res = Math.max(res, dp[kx][ky]);

                    // 将该行最远距离的变化暂存在rowTemp，保持rowMax不变
                    rowTemp[kx] = Math.max(rowTemp[kx], dp[kx][ky]);
                    colTemp[ky] = Math.max(colTemp[ky], dp[kx][ky]);
                }
                // dp计算后将rowMax值更新
                for(int j = 0; j < n; j ++){
                    rowMax[j] = rowTemp[j];
                }
                for(int j = 0; j < m; j ++){
                    colMax[j] = colTemp[j];
                }
                i = r - 1;
            }
            // 不同元素情况直接计算
            else{
                dp[x][y] = Math.max(rowMax[x], colMax[y]) + 1;
                res = Math.max(res, dp[x][y]);
                rowMax[x] = dp[x][y];
                colMax[y] = dp[x][y];
            }
        }
        return res;
    }
}

---

相同元素处理部分写的比较繁琐了