【C++算法】——高精度（加，减，乘，除）

news2025/1/12 16:15:00

前言

高精度算法就是为了去解决一些比较大的数，这些数大到long long都存不下。，这里的主要思想就是用字符串来存。

下面的内容有很多用到c++的容器，不明白的可以先去学习stl。

一  高精度加法

首先第一步就是去模拟我们自己写的加法，，从我们自己写的加法上面来看，第一它是从个位开始加，如果大于10就会产生进位，这个进位要加到下一位去。

我们写加法是从个位开始，但是用代码去写，就需要倒过来，因为个位是不好去进位的，如果用个位去进位，那么就会导致整块的移动，这样效率就会很低了

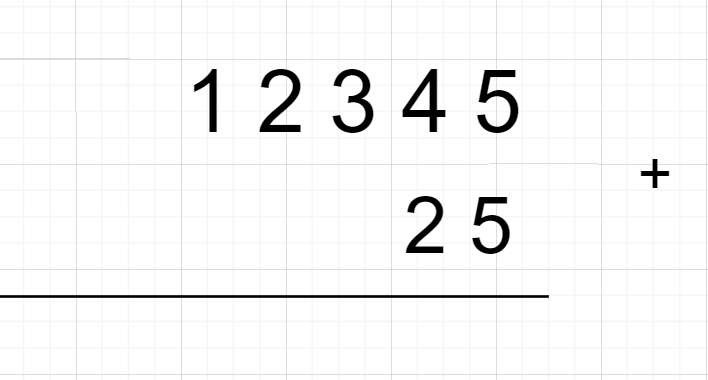
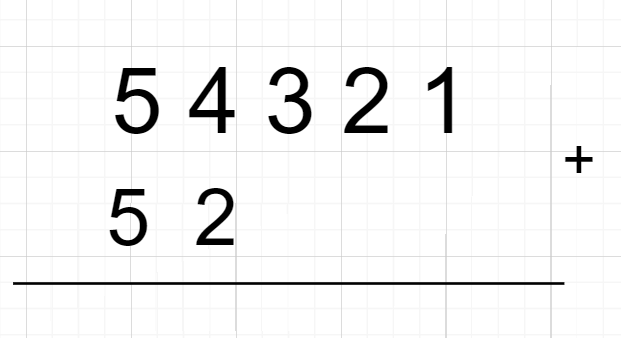
图一是我们自己算，图二则是我们用代码去实现的过程

所以有了上面的准备，就可以写出下面代码

#include<iostream>
#include<vector>
using namespace std;

vector<int> add(const vector<int>& A, const vector<int>& B)//加法函数，这里传引用是为了提高效率
{
	int t = 0;
	vector<int>C;//用来返回
	for (int i = 0; i < A.size(); i++)//因为之前已经逆序了，所以这里直接从0开始遍历
	{
		t +=A[i];//首先把最长的数的最后一位加上
		if (i < B.size()) t += B[i];//因为B短，所以我们需要去判断B是否已经结束
		C.push_back(t % 10);//最后我们是插入t%10,如果大于就进位，小于就不进位
		t /= 10;//这里相当于是进位的过程
	}
	if (t) C.push_back(1);//还有A结束的时候，可能还有一个进位没有处理，这里把它尾插
	return C;
}


int main()
{
	string a, b;
	vector<int>A, B, C;
	cin >> a >> b;
	for (int i = a.size()-1; i >=0; i--)//逆置
	{
		A.push_back(a[i] - '0');//转换
	}
	for (int i = b.size() - 1; i >= 0; i--)
	{
		B.push_back(b[i] - '0');
	}

	if (A.size() > B.size()) C = add(A, B);//这里是调整A,B那个数长，长的放上面，比较好操作
	else C = add(B, A);

	for (int i = C.size()-1; i >= 0; i--)//因为是逆序相加的，所以这里需要再逆序倒过来输出
	{
		cout << C[i];
	}
	cout << endl;

	return 0;

}

 主函数里面的处理还是比较简单的，关键在于两个数的相加

二  高精度减法

其实减法也差不多，一样的反转，但是不同的就是我们需要用一个数去存一个借位，而不是进位，因为一个数减另外一个数不够我们就需要去借位，这样才能够减，第二就是我们在进行减法的时候需要的是去判断两个数的大小哪个更加大，而不是和加法一样去判断长度。

一样的，下面看代码理解

bool cmp(vector<int>& A, vector<int>& B)//比较函数
{
	if (A.size() != B.size())
		return A.size() > B.size();
	for (int i = A.size() - 1; i >= 0; i--)
	{
		if (A[i] != B[i])
			return A[i] > B[i];
	}
    return true;
}

vector<int> sub(vector<int>& A, vector<int>& B)//减法函数
{
	int t = 0;
	vector<int>C;
	for (int i = 0; i < A.size(); i++)
	{
		t = A[i] - t;//一开始没有借位
		if (i < B.size()) t -= B[i];
		C.push_back((t + 10) % 10);//这个是如果t>0,说明没有借位，如果小于0，就借位了
                                   //这里+10是先算它进位，然后再%10,如果没有进位，那就是它本身
                                   //如果进位了，那我们插入的就是10-t;
		if (t < 0) t = 1;//借位等于1，下次循环，A[i]就需要-1
		else t = 0;
	}
	while (C.size() > 1 && C.back() == 0)C.pop_back();//这里需要去掉前导零
	return C;
}
int main()
{
	string a, b;
	vector<int>A, B, C;
	cin >> a >> b;
	for (int i = a.size()-1; i >=0; i--)//这里操作和加法是一样的
	{
		A.push_back(a[i] - '0');
	}
	for (int i = b.size() - 1; i >= 0; i--)
	{
		B.push_back(b[i] - '0');
	}
	if (cmp(A, B)) C = sub(A, B);//这是判断大小
	else C = sub(B, A), cout << '-';//如果A小于B,那么我们可以换成-（B-A）
                                    //这里要多输出一个符号

	for (int i = C.size()-1; i >= 0; i--)
	{
		cout << C[i];
	}
	cout << endl;

	return 0;

}

三  高精度乘法

关于高精度乘法来说，就没有减法那么多处理了，甚至比加法还简单一点，这里的乘法是一个多位数和一个低位数的相乘

vector<int> mul(vector<int>& A, int b)
{
	int t = 0;
	vector<int>C;
	for (int i = 0; i < A.size(); i++)
	{
		t += A[i] * b;//t是进位
		C.push_back(t % 10);
		t /= 10;
	}
	if (t) C.push_back(t);//最后一位有进位就插入
	while (C.size() > 1 && C.back() == 0) C.pop_back();//处理前导零
	return C;
}

int main()
{
	string a;//这里直接正常操作就行
	int b;
	vector<int>A, C;
	cin >> a >> b;
	for (int i = a.size()-1; i >=0; i--)
	{
		A.push_back(a[i] - '0');
	}
	C = mul(A, b);
	for (int i = C.size()-1; i >= 0; i--)
	{
		cout << C[i];
	}
	cout << endl;

	return 0;

}

 

四  高精度除法

这里的除法和其他的又有点不一样，但是不一样的不会很多，第一就是我们除一个数可能除不尽，所以这里需要一个余数去存。

vector<int> div(vector<int>& A, int b,int &r)
{
	r = 0;
	vector<int>C;
	for (int i = A.size()-1; i >= 0; i--)//这里和其他的不一样，因为我们除法只能从个位开始除
	{
		r = r * 10 + A[i];//这里表示余数和下一个数的相加
		C.push_back(r / b);
		r %= b;
	}
	reverse(C.begin(), C.end());//这里因为上面的操作把C变为正序了，所以这里要反过来，因为
                                //后面打印是按逆序打印，这里就和上面同一了
	while (C.size() > 1 && C.back() == 0)C.pop_back();//去前导零
	return C;
}

int main()
{
	string a;
	int b;
	vector<int>A, C;
	cin >> a >> b;
	for (int i = a.size()-1; i >=0; i--)//这里操作和上面差不多
	{
		A.push_back(a[i] - '0');
	}
	int r;
	C = div(A, b,r);
	for (int i = C.size()-1; i >= 0; i--)
	{
		cout << C[i];
	}
	cout << endl;
	cout << r;
	

	return 0;

}

五 练习

a-b

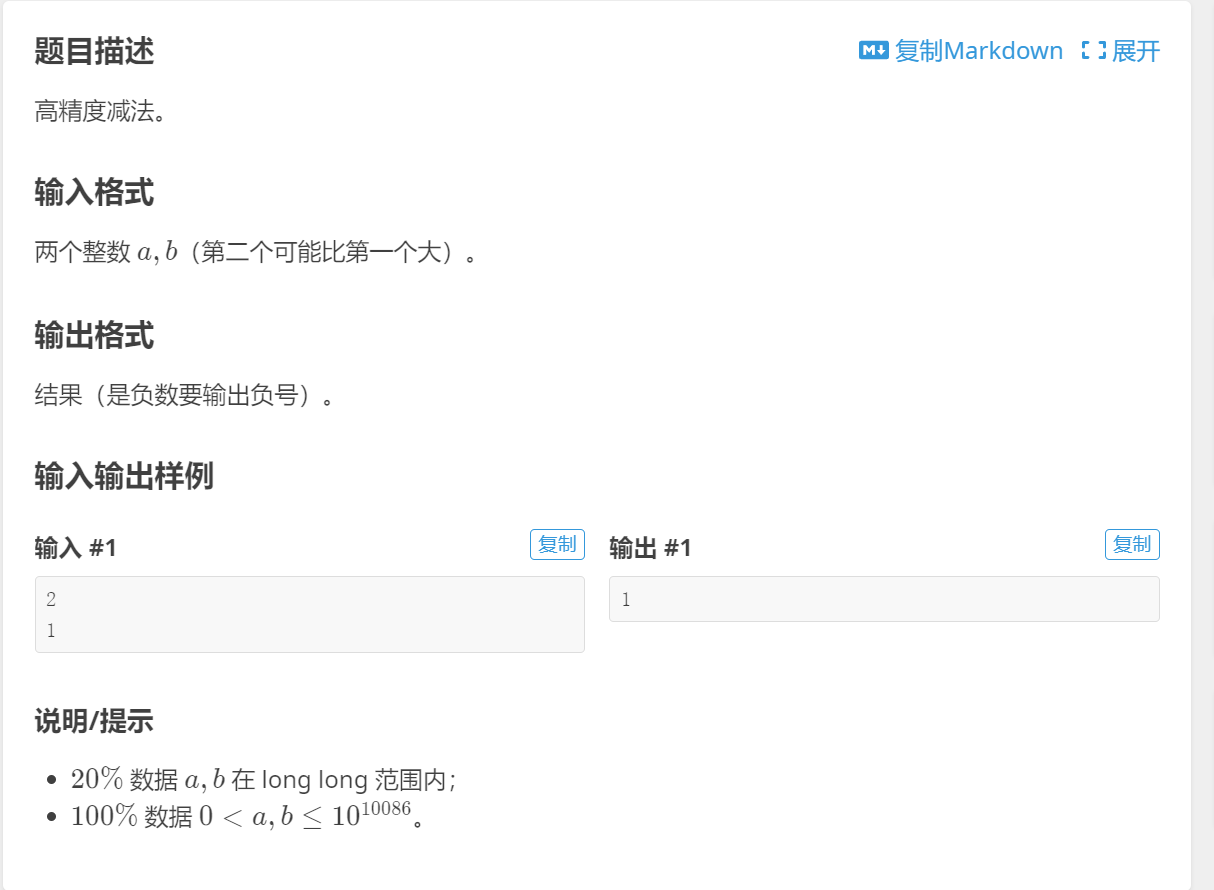
这里直接用上面的代码就行

 

#include <iostream>
#include <vector>

using namespace std;
bool cmp(vector<int>& A, vector<int>& B)//比较函数
{
	if (A.size() != B.size())
		return A.size() > B.size();
	for (int i = A.size() - 1; i >= 0; i--)
	{
		if (A[i] != B[i])
			return A[i] > B[i];
	}
    return true;
}

vector<int> sub(vector<int>& A, vector<int>& B)//减法函数
{
	int t = 0;
	vector<int>C;
	for (int i = 0; i < A.size(); i++)
	{
		t = A[i] - t;//一开始没有借位
		if (i < B.size()) t -= B[i];
		C.push_back((t + 10) % 10);//这个是如果t>0,说明没有借位，如果小于0，就借位了
                                   //这里+10是先算它进位，然后再%10,如果没有进位，那就是它本身
                                   //如果进位了，那我们插入的就是10-t;
		if (t < 0) t = 1;//借位等于1，下次循环，A[i]就需要-1
		else t = 0;
	}
	while (C.size() > 1 && C.back() == 0)C.pop_back();//这里需要去掉前导零
	return C;
}
int main()
{
	string a, b;
	vector<int>A, B, C;
	cin >> a >> b;
	for (int i = a.size()-1; i >=0; i--)//这里操作和加法是一样的
	{
		A.push_back(a[i] - '0');
	}
	for (int i = b.size() - 1; i >= 0; i--)
	{
		B.push_back(b[i] - '0');
	}
	if (cmp(A, B)) C = sub(A, B);//这是判断大小
	else C = sub(B, A), cout << '-';//如果A小于B,那么我们可以换成-（B-A）
                                    //这里要多输出一个符号

	for (int i = C.size()-1; i >= 0; i--)
	{
		cout << C[i];
	}
	cout << endl;

	return 0;

}

a+b

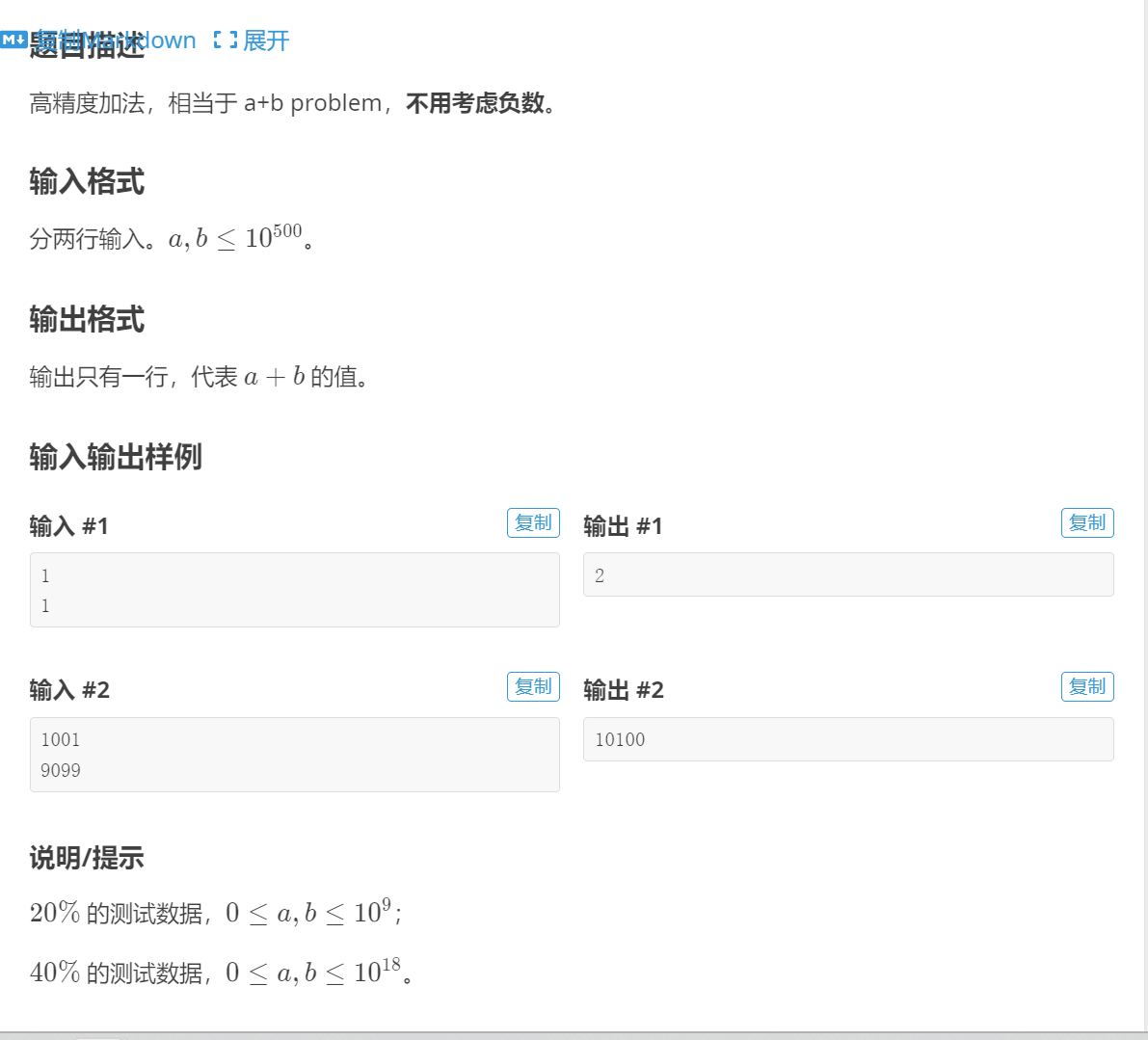
#define _CRT_SECURE_NO_WARNINGS 1
#include<iostream>
#include<vector>
using namespace std;
const int N = 1e6 + 10;
vector<int>add(vector<int>& A, vector<int>& B)
{
	vector<int>C;
	int t = 0;
	for (int i = 0; i < A.size() || i < B.size(); i++)
	{
		if (i < A.size()) t += A[i];
		if (i < B.size()) t += B[i];
		C.push_back(t % 10);
		t /= 10;
	}
	if (t)
	C.push_back(1);
	return C;

}
int main()
{
	string a, b;
	cin >> a >> b;
	vector<int>A, B;
	for (int i = a.size() - 1; i >= 0; i--) A.push_back(a[i] - '0');
	for (int i = b.size() - 1; i >= 0; i--) B.push_back(b[i] - '0');
	vector<int>C;
	C = add(A, B);
	for (int i = C.size() - 1; i >= 0; i--)
	{
		cout << C[i];
	}
	return 0;
}

 

六  总结

以上高精度算法，加法和乘法比较简单，除法和减法需要一点细节理解

加法没有去前导零的操作，其他都有，以上就是高精度的全部内容了，希望对你有所帮助

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/1854263.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

vlan三层交换技术--交换机--(自作)

vlan三层交换技术--交换机--(自作)

阅读更多...
全面理解-Flutter（万字长文，深度解析）

全面理解-Flutter（万字长文，深度解析）

1、Web 性能差&#xff0c;跟原生 App 存在肉眼可见的差距&#xff1b; 2、React Native 跟 Web 相比&#xff0c;支持的能力非常有限&#xff0c;特定长场景问题&#xff0c;需要三端团队一个一个处理&#xff1b; 3、Web 浏览器的安卓碎片化严重&#xff08;感谢 X5&#x…
阅读更多...
Java内存泄漏检测和分析介绍

Java内存泄漏检测和分析介绍

在Java中&#xff0c;内存泄漏检测和分析是一个重要的任务&#xff0c;可以通过以下几种方式进行&#xff1a; 1. 使用VisualVM VisualVM是一个可视化工具&#xff0c;可以监控、分析Java应用程序的内存消耗。它可以显示堆内存、垃圾收集、线程等信息&#xff0c;并且可以对内…
阅读更多...
两个基因相关性细胞系（CCLE）（升级）

两个基因相关性细胞系（CCLE）（升级）

目录 单基因CCLE数据 ①细胞系转录组CCLE数据下载 ②单基因泛癌表达 CCLE两个基因相关性 ①进行数据整理 ②相关性分析 单基因CCLE数据 ①细胞系转录组CCLE数据下载 基因在各个细胞系表达情况_ccle expression 23q4-CSDN博客 rm(list = ls()) library(tidyverse) libra…
阅读更多...
体验了一下AI生产3D模型有感

体验了一下AI生产3D模型有感

我的实验路子是想试试能不能帮我建一下实物模型 SO 我选择了一个成都环球中心的网图 但是生成的结果掺不忍睹&#xff0c;但是看demo来看&#xff0c;似乎如果你能给出一张干净的提示图片&#xff0c;他还是能做出一些东西的 这里我延申的思考是这个物体他如果没看过背面&…
阅读更多...
43 mysql insert select 的实现

43 mysql insert select 的实现

前言 我们这里 来探讨一下 insert into $fields select $fields from $table; 的相关实现, 然后 大致来看一下 为什么 他能这么快 按照 我的思考, 应该里里面有 批量插入才对, 但是 调试结果 发现令我有一些意外 呵呵 果然 只有调试才是唯一的真理 测试数据表如下 CREATE…
阅读更多...
win10 安装openssl并使用openssl创建自签名证书

win10 安装openssl并使用openssl创建自签名证书

win10创建自签名证书 下载安装配置openssl 下载地址&#xff1a; https://slproweb.com/download/Win64OpenSSL-3_3_1.exe https://slproweb.com/products/Win32OpenSSL.html 完成后安装&#xff0c;一路next&#xff0c;到达选位置的之后选择安装的位置&#xff0c;我这里选…
阅读更多...
解决文件或文件夹无法删除问题

解决文件或文件夹无法删除问题

最近呢&#xff0c;发现很多小伙伴都会遇到一个问题&#xff0c;就是当我要删掉一个文件或者软件的时候&#xff0c;就会弹出[操作无法完成&#xff0c;因为其中的文件夹或文件已在另一个程序中打开] 然后我就翻看网站&#xff0c;很多都是什么去**[任务管理器]修改[资源管理器…
阅读更多...
视频讲解|【双层模型】分布式光伏储能系统的优化配置方法

视频讲解|【双层模型】分布式光伏储能系统的优化配置方法

1 主要内容 该讲解视频对应的程序链接为【双层模型】分布式光伏储能系统的优化配置方法&#xff0c;模型参考《分布式光伏储能系统的优化配置方法》&#xff0c;分为上下层求解方式&#xff0c;上层采用粒子群算法确定储能的选址和容量方案&#xff0c;以全年购电成本、网络损…
阅读更多...
超详细！想进华为od的请疯狂看我！

超详细！想进华为od的请疯狂看我！

三分钟带你全面了解华为OD 【合同及管理】签约方为科锐国际/外企德科&#xff08;人力服务公司&#xff09;&#xff0c;劳动合同期为4年&#xff0c;试用期6个月。员工关系合同管理、五险一金、考勤发薪由科锐国际/外企德科负责&#xff1b;定级定薪、员工培训、工作安排、绩…
阅读更多...
matplotlib之savefig函数

matplotlib之savefig函数

savefig函数 Matplotlib中&#xff0c;savefig函数用于保存图形为文件。通过该函数&#xff0c;你可以将绘制的图形保存为常见的图像文件格式&#xff0c;如PNG、JPEG、SVG等。 matplotlib.pyplot.savefig(fname, dpiNone, bbox_inchestight, pad_inches0.1, formatNone, tra…
阅读更多...
【Linux】进程间通信_1

【Linux】进程间通信_1

文章目录 七、进程间通信1. 进程间通信分类管道 未完待续 七、进程间通信 进程间由于 进程具有独立性 &#xff0c;所以不可以直接进行数据传递。但是我们通常需要多个进程协同&#xff0c;共同完成一件事&#xff0c;所以我们需要进程间通信的手段。进程间通信的本质就是先让…
阅读更多...
PAL: Program-aided Language Models

PAL: Program-aided Language Models

PAL: Program-aided Language Models ArXiv&#xff1a;https://arxiv.org/pdf/2211.10435 GitHub&#xff1a;https://reasonwithpal.com/ 一、动机 大模型与Chain-of-Thought可以很好地将一些复杂的问题分解为若干个子问题并进行逐步推理&#xff1b;但是对于一些较为复杂…
阅读更多...
C/C++ strftime函数

C/C++ strftime函数

目录 strftime()函数 函数原型 头文件 功能 返回值 参数 案例 结语 strftime()函数 函数原型 size_t strftime(char *s, size_t max, const char *format, const struct tm *tm); 头文件 #include <time.h> 功能 用于日期和时间格式化的函数&#xff0c;它允许你…
阅读更多...
openjudge_2.5基本算法之搜索_917:Knight Moves

openjudge_2.5基本算法之搜索_917:Knight Moves

题目 917:Knight Moves 总时间限制: 1000ms 内存限制: 65536kB 描述 Background Mr Somurolov, fabulous chess-gamer indeed, asserts that no one else but him can move knights from one position to another so fast. Can you beat him? The Problem Your task is to wr…
阅读更多...
卡尔曼滤波-剔除异常值的影响

卡尔曼滤波-剔除异常值的影响

二郎在看论文的时候&#xff0c;发现了一个针对卡尔曼滤波过程中&#xff0c;测量向量出现误差导致滤波发散的处理方法。 该方法也可以扩展到其他问题中使用&#xff0c;所以二郎在这里写一下。 论文原文&#xff1a;https://www.mdpi.com/1424-8220/20/17/4710 论文翻译对应…
阅读更多...
DS：二叉树的链式存储及遍历

DS：二叉树的链式存储及遍历

​ 欢迎来到Harper.Lee的学习世界&#xff01; 博主主页传送门&#xff1a;Harper.Lee的博客主页 想要一起进步的uu可以来后台找我哦&#xff01; ​ 一、引入 1.1 二叉树的存储方式 在之前接触到的满二叉树和完全二叉树使用的是数组的存储方式&#xff08;DS&#xff1a;树与…
阅读更多...
HarmonyOS SDK助力鸿蒙原生应用“易感知、易理解、易操作”

HarmonyOS SDK助力鸿蒙原生应用“易感知、易理解、易操作”

6月21-23日&#xff0c;华为开发者大会&#xff08;HDC 2024&#xff09;盛大开幕。6月23日上午&#xff0c;《HarmonyOS开放能力&#xff0c;使能应用原生易用体验》分论坛成功举办&#xff0c;大会邀请了多位华为技术专家深度解读如何通过根技术、开放能力、场景化控件等亮点…
阅读更多...
越复杂的CoT越有效吗？Complexity-Based Prompting for Multi-step Reasoning

越复杂的CoT越有效吗？Complexity-Based Prompting for Multi-step Reasoning

Complexity-Based Prompting for Multi-step Reasoning 论文&#xff1a;https://openreview.net/pdf?idyf1icZHC-l9 Github&#xff1a;https://github.com/FranxYao/chain-of-thought-hub 发表位置&#xff1a;ICLR 2023 Complexity-Based Prompting for Multi-step Reason…
阅读更多...
C#基于SkiaSharp实现印章管理（1）

C#基于SkiaSharp实现印章管理（1）

最近对着微软的教程学习SkiaSharp的概念及用法&#xff0c;由于之前使用GDI绘制过坐标系、印章等程序&#xff0c;准备使用SkiaSharp、SKControl控件编写简单的印章设计功能&#xff0c;并能用印章对图片盖章。本文实现创建印章背景、序列化及反序列化印章对象等功能。   VS2…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023