欢迎来到Harper.Lee的学习世界！
博主主页传送门：Harper.Lee的博客主页
想要一起进步的uu可以来后台找我哦！
一、引入
1.1 二叉树的存储方式
在之前接触到的满二叉树和完全二叉树使用的是数组的存储方式（DS：树与二叉树的相关概念）：二叉树因为是顺序结构，比较适合数组形式的存储，但如果不是这两种树形结构，而是其他非完全二叉树，如果用数组实现，那数组的中间部分就可能会存在大量的空间浪费，因此就不适合数组存储，而采用的是链式存储方式。
二叉树使用的是链式结构存储，即使用链表来存储二叉树，就不会有上述的缺陷。链式结构中有左孩子指针和右孩子指针，如果少了左孩子或者右孩子，就让相应的指针置为NULL即可。
虽然链式结构可以表示所有类型的二叉树，但是由于二叉树本身存储数据的价值并不大（链表、顺序表远远优于二叉树），所以实现增删查改是没有太大意义的，学习链式二叉树真正的意义是学会如何去控制、遍历二叉树的结构，为我们后期学习搜索二叉树做好铺垫。而以下的学习中要重点理解二叉树中的递归思想和分治思想!
1.2 二叉树的应用之一——搜索二叉树
二叉树常用的应用方式就是搜索二叉树，搜索二叉树的特点：左子树的所有值比根节点小，右子树的所有值比根节点大，如下图。（左子树<根<右子树）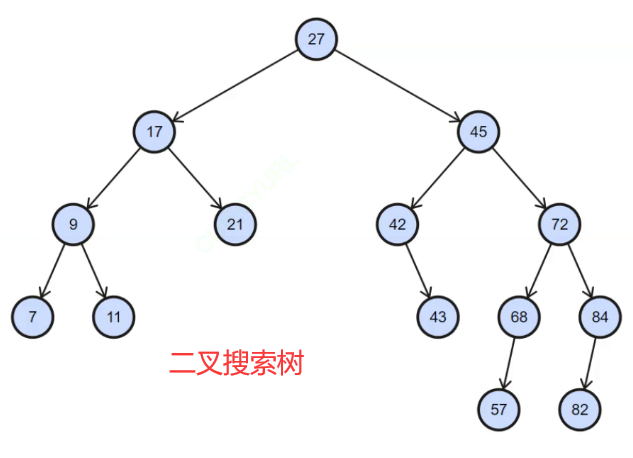
为什么叫二叉搜索树呢？顾名思义，它有数据的搜索功能。例如，查找数据43：43比27大，搜索范围变成右子树，43比45小，搜索范围在左子树，43比42大，搜索范围在右子树，43=43，查找到该数据，且搜索范围逐渐缩小了。
这种查找方式有点类似于二分法，但是二者有很大的不同，搜索二叉树比它效率高好几倍：
| 对比 | 1. 二分法 | 2. 二叉搜索树 |
|---|---|---|
| 数据的存储方式 | 数组存储，增删查改效率低：可能会涉及到数据的挪动等 | 左子树的所有值比根节点小，右子树的所有值比根节点大 可适用于各种类型的数据，但同一棵树中的数据是同一类型 |
| 要求 | 需要排序：排序本身消耗就大 | 不要求排序，兄弟之间无序，父子之间谁大谁当爹或者谁小谁当爹 |
| 二分法在实际中本就不常用 | 二叉搜索树的最大缺陷：不适用于单支的树状结构（如下图） |
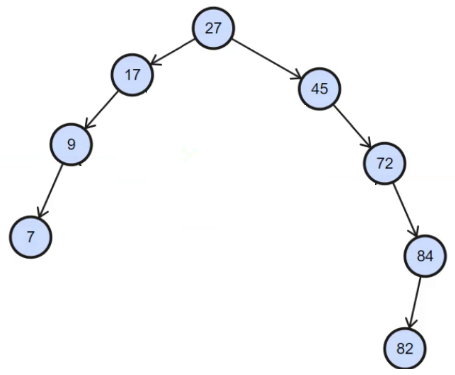
本次搜索二叉树的学习主要有两个目的：1. 最注重的是为后面的学习打基础：对于二叉树的学习，不只是有搜索二叉树，还有AVL树红黑树等二叉平衡搜索树、B数系列多叉平衡搜索树等，他们的基础都在搜索二叉树上。2. 本次学习重点还需要理解二叉树中的递归思想和分治思想。
二、链式二叉树的实现
2.1 相关结构体
typedef int BTDataType;
typedef struct BinaryTreeNode
{
BTDataType data;//二叉树节点的数据域
struct BinaryTreeNode* left;//左孩子
struct BinaryTreeNode* right;//右孩子
}BTNode;//重命名为比较简单的名字
2.2 手搓一棵树
在之前学习链表的时候，我们是先插入数据来进行对实现的功能的测试；数组测试我们可以直接给一个数组。同样在这里首先我们需要创建一棵树，才能进行测试，二叉树的增删查改没啥意义，加入二叉搜索树后就有意义了。手搓二叉树只是为了方便测试。
//手搓一棵二叉树
BTNode* CreatBinaryTree()
{
//1. 先创建6个节点
BTNode* node1 = BuyNode(1);//2. BuyNode节点创建函数的实现
BTNode* node2 = BuyNode(2);
BTNode* node3 = BuyNode(3);
BTNode* node4 = BuyNode(4);
BTNode* node5 = BuyNode(5);
BTNode* node6 = BuyNode(6);
//3. 用left、right连接节点，使其变成自己想要的树的形状
node1->left = node2;
node1->right = node4;
node2->left = node3;
node4->left = node5;
node4->right = node6;
return node1;//直接返回根节点，有了根节点，就有了左膀右臂，直接开火车就可以找到整棵树
}
三、遍历
链式二叉树的增删查改操作没有太大的实际意义，因此我们主要探索的是它的遍历方式。**对于任意一棵树，访问的顺序有三种：前序（前根遍历）、中序（中根遍历）、后序（后根遍历）。 **
3.1 前序遍历(Preorder Traversal )
3.1.1 代码实现
//前序遍历
void PrevOrder(BTNode* root)
{
//1. 判空
if (root == NULL)
{
printf("N ");//为空的地方打印N，这样更能表示出访问的位置
return;
}//可以不写else
//2. 开始前序遍历
//3. 先访问根（打印根节点的数据）
printf("%d ", root->data);
//4. 再访问左子树left
PrevOrder(root->left);
//5. 最后访问右子树
PrevOrder(root->right);
}
3.1.2 分析过程
逻辑过程分析（使用代码进行分析）：这里其实就是在重复执行一套指令，只不过我为了更加形象地描述它，选择了用代码展开分析讨论。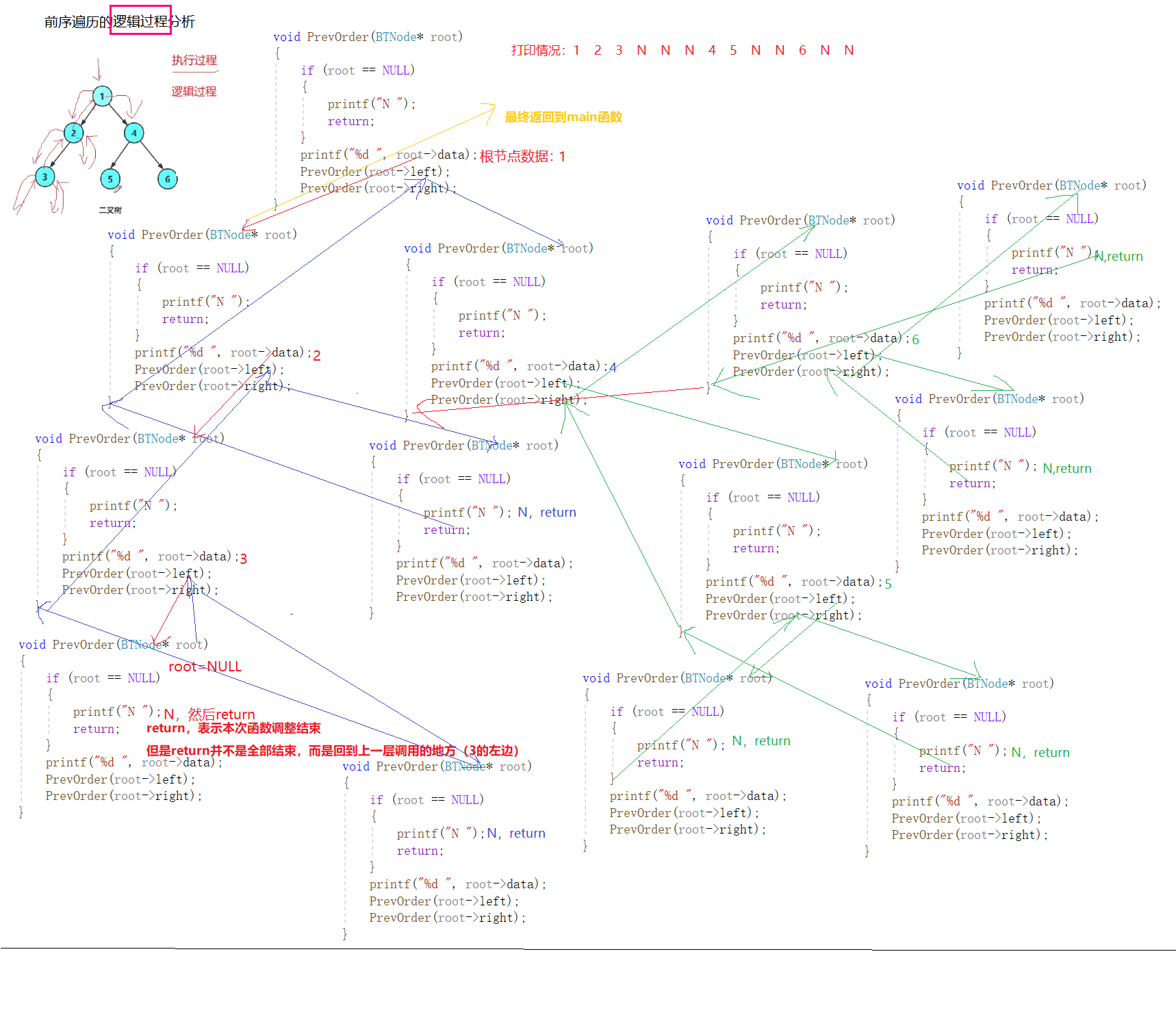
物理过程分析：函数调用是建立栈桢的过程，每个函数调用都是独立的栈桢，调用结束，栈桢销毁。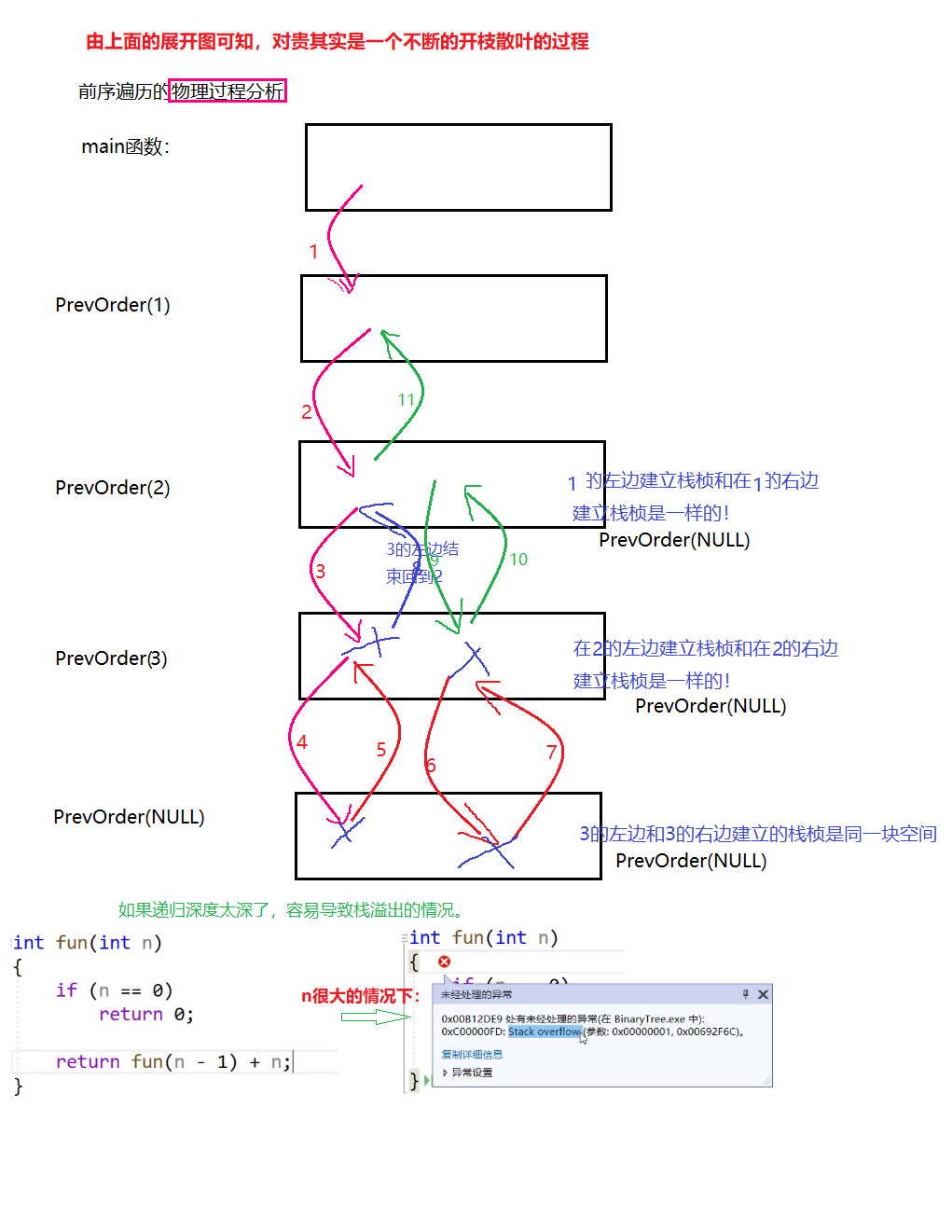
如果递归深度太深了，容易导致栈溢出的情况。 如上图的最后。
根据上述画图中，我们可以知道，PrevOrder函数的递归调用过程中一直在重复使用同一套指令。一套指令重复使用多次，只是每次传入的参数不同，参数不同，执行的逻辑就不同，树状开枝散叶的成都也就不同。此过程中，函数递归的调用并不是死循环的调用，它会遇到NULL，通过return结束该小部分的函数调用，返回上一个调用的函数。
此外，函数递归调用时的参数是存储在栈中的。每个函数调用都是独立的栈桢，栈桢之间相互独立。
3.2 中序遍历(Inorder Traversal)
中序遍历分析的逻辑过程、逻辑过程和前序遍历是一样的分析方法，只需照猫画虎即可。
//中序遍历
void InOrder(BTNode* root)
{
if (root == NULL)
{
printf("N ");
return;
}
InOrder(root->left);
printf("%d ", root->data);
InOrder(root->right);
}
3.3 后序遍历(Postorder Traversal)
后序遍历的物理过程和逻辑过程和前序遍历的分析方式一样。
3.4 层序遍历(BFS)
层序遍历是一种广度优先遍历(BFS)，
四、对树的相关计算
4.1 递归的分治思想
我们一般在没写出代码的时候就很难画出像3.1.2那样的分析图的，因此，在不知道代码如何写的情况下，我们选择递归的分治思想，大概分析出整个过程的思维框架，以便于更好地写出代码。下图是以树的节点个数为例子的一种分析过程：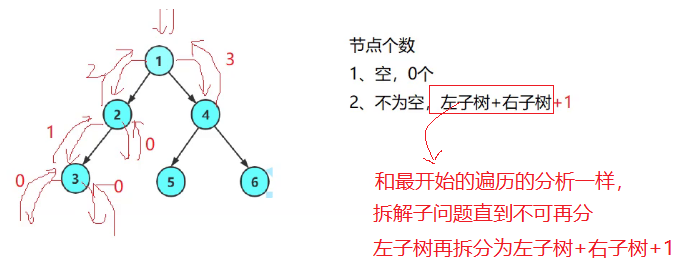
根据上图再逐步接触对应的代码。
//分治思想求树的节点个数
int TreeSize(BTNode* root)
{
return root == NULL ? 0 : TreeSize(root->left) + TreeSize(root->right) + 1;
}
分治，即分而治之，类似于上下级的管理。例如校长要求学校中统计在校学生人数、在校师生人数等。校长肯定不是自己挨个地去数人数，而是通过各种管理层统计后进行汇总。就像各个班长汇总数据给辅导员，各个辅导员汇总数据给院长，各个院长再汇总数据给校长，校长就得到了最终的数据。
在这个管理层中，级别最低的就是没当班长的学生，他们就是这个管理树中的叶子节点。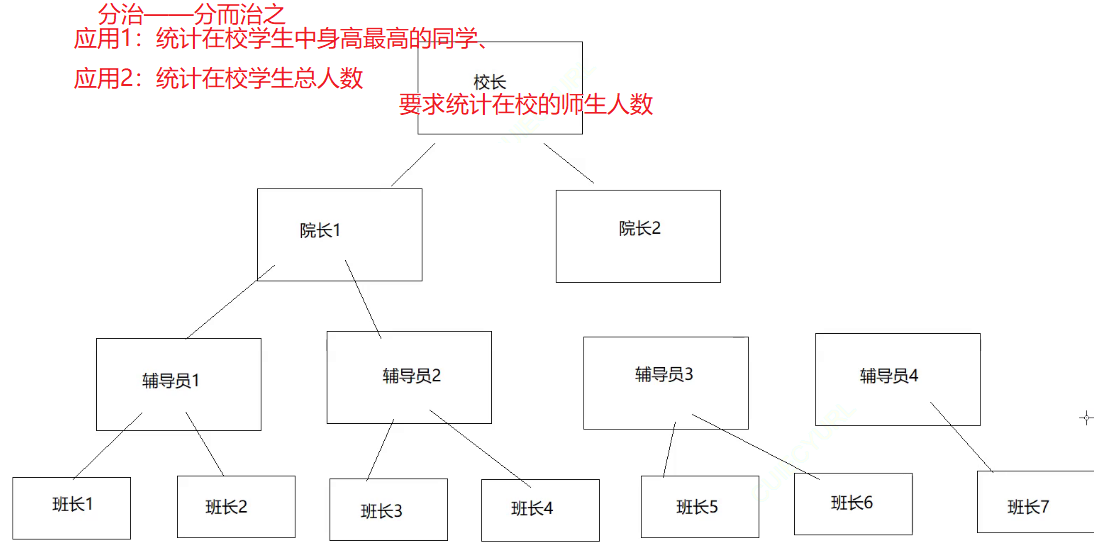
4.2 求树的节点个数
（1）错误代码
//求节点个数的错误代码
int TreeSzie(BTNode* root)
{
static int size = 0;
//size定义为静态变量:局部静态只会初始化一次，即在第一次的时候才会初始化，其他都是直接积累就用了
//如果树为空树
if (root == NULL)
return 0;
else
++size;
//树不是空树
//开始遍历（遍历方式随便一种，这里是前序遍历）
TreeSzie(root->left);
TreeSzie(root->right);
return size;
}
（2）正确代码
a. 定义全局变量
//求节点个数
int size = 0;//定义为全局变量
int TreeSzie(BTNode* root)
{
//如果树为空树
if (root == NULL)
return 0;
else
++size;
//树不是空树
//开始遍历（遍历方式随便一种，这里是前序遍历）
TreeSzie(root->left);
TreeSzie(root->right);
return size;
}
b. 定义指针
int TreeSize(BTNode* root,int* psize)
{
if (root == NULL)
return 0;
else
++(*psize);
//遍历树的任一方式：
TreeSize(root->left, psize);
TreeSize(root->right, psize);
return *psize;//可以不用返回值，返回类型为void
}
4.3 二叉树的叶子节点个数
注意不要忽略空树的情况，空树进入函数，->相当于解引用，堆空指针解引用报错！
//求叶子节点的个数
int TreeLeafSize(BTNode* root)
{
if (root == NULL)
return 0;
else if (root->left && root->right)
return 1;
else
return TreeLeafSize(root->left) + TreeLeafSize(root->right);
}
4.4 二叉树的高度
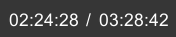
欲扬先抑，要求这个，我就先找下面另外一个，就像校长统计在校师生人数一样，校长直接找各位院长得到数据+1汇总，而院长直接就是各位辅导员数据+1汇总，辅导员数据为班长数据+1（班长自己），层层向下，就像命令在传递一样。班长得到数据后返回辅导员，辅导员得到班长数据后返回院长，院长得到辅导员数据后返回校长，整个过程一来一回，数据就统计出来了。
//求树的高度
int TreeHeight(BTNode* root)
{
if (root == NULL)
return 0;
else
return TreeHeight(root->left) > TreeHeight(root->right) + 1 ?
TreeHeight(root->left) : TreeHeight(root->right) + 1;
}
缺陷：如果该二叉树是一个节点的高度很大的树，那么每个位置会出现重复计算的情况，且重复计算并不一定是两次，可能会重复计算多次。因此我们需要用变量记录每次计算的结果，若还需要该结果，可直接使用该变量。就是在这一点上，我们常常错误的认为重复计算两次即时间消耗为2倍，其实时间消耗远不止2倍。分析过程如下图。
//求树的高度
//时间复杂度：O(N)
int TreeHeight(BTNode* root)
{
if (root == NULL)
return 0;
//保存记录数据
int leftHeight = TreeHeight(root->left);
int rightHeight = TreeHeight(root->right);//可以使用fmax函数
return leftHeight > rightHeight ? leftHeight + 1 : rightHeight + 1;
}
这就相当于不记事的某一层领导因为忘记数据，又再安排下层领导一次，该领导这条路就又重复一次。
4.5 二叉树查找值为x的节点
（1）分析过程如下：
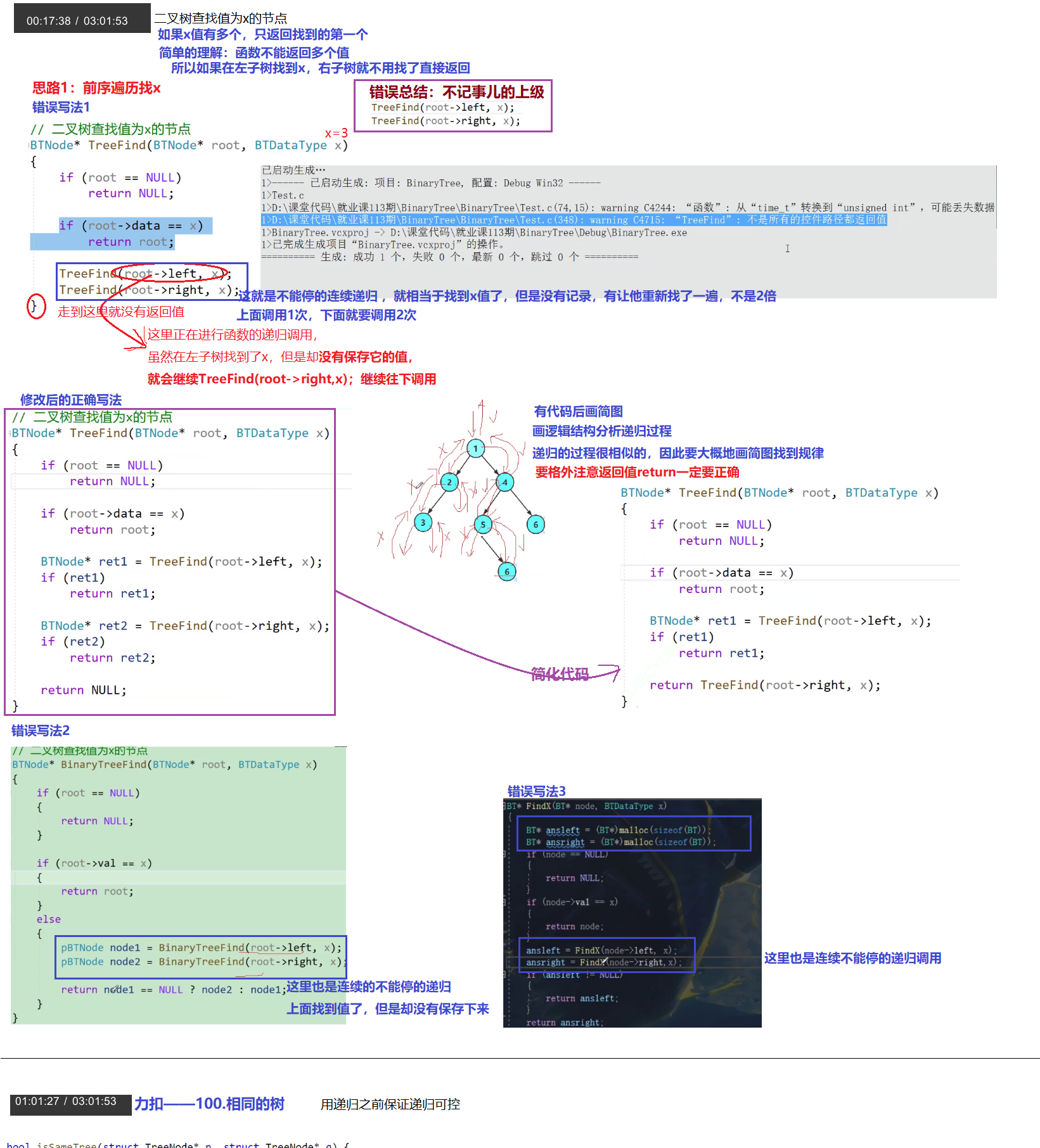
（2）代码实现
//二叉树中查找值为x的节点
BTNode* BinaryTreeFind(BTNode* root, BTDataType x)
{
if (root == NULL)
retur NULL;
if (root->data == x)
return root;
BTNode* ret1 = BinaryTreeFind(root->left, x);
if (ret1)
return ret1;
BTNode* ret2 = BinaryTreeFind(root->right, x);
if (ret2)
return ret2;
return NULL;
}
改进版本：
//改进版本：
BTNode* _BinaryTreeFind(BTNode* root, BTDataType x)
{
if (root == NULL)
retur NULL;
if (root->data == x)
return root;
BTNode* ret1 = _BinaryTreeFind(root->left, x);
if (ret1)
return ret1;
return _BinaryTreeFind(root->right, x);
}
喜欢的朋友记得三连支持哦！
