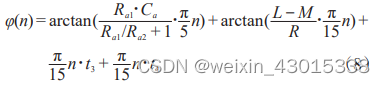数据的预处理(Data Preprocessing)
2 Data Preprocessing数据的预处理
数据预处理的几种方法
2,1 数据的零点中心化
数据的零点中心化的目的就是为了把数据的整体分布拉回到原点附近,也就是让数据的整体均值变为0。
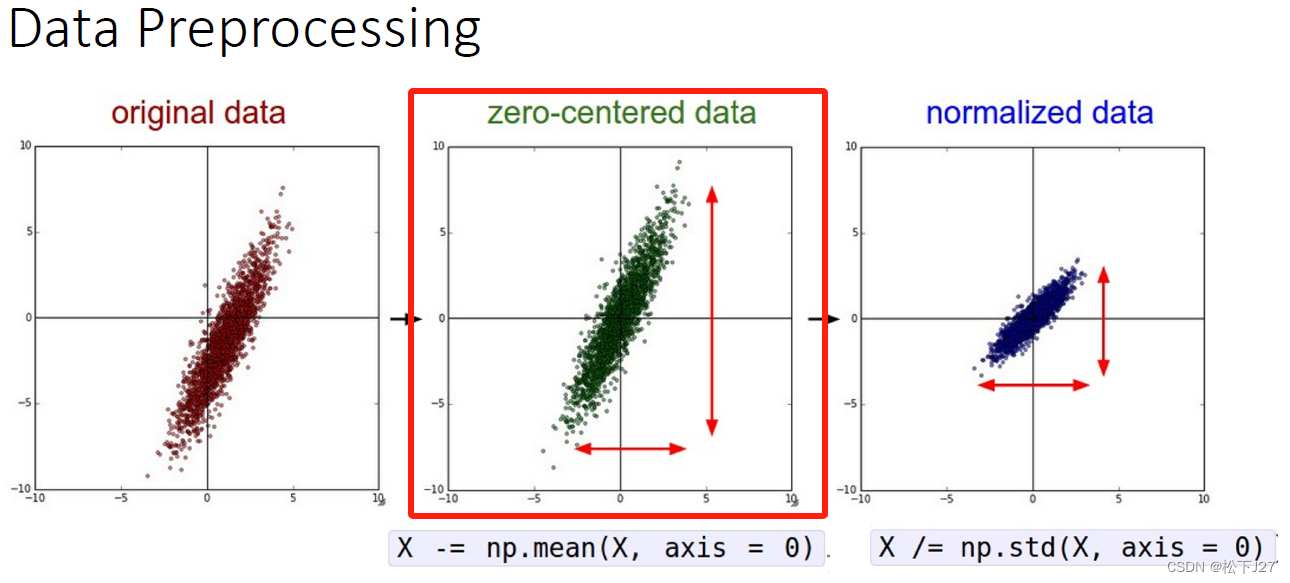
2,2 数据的标准化
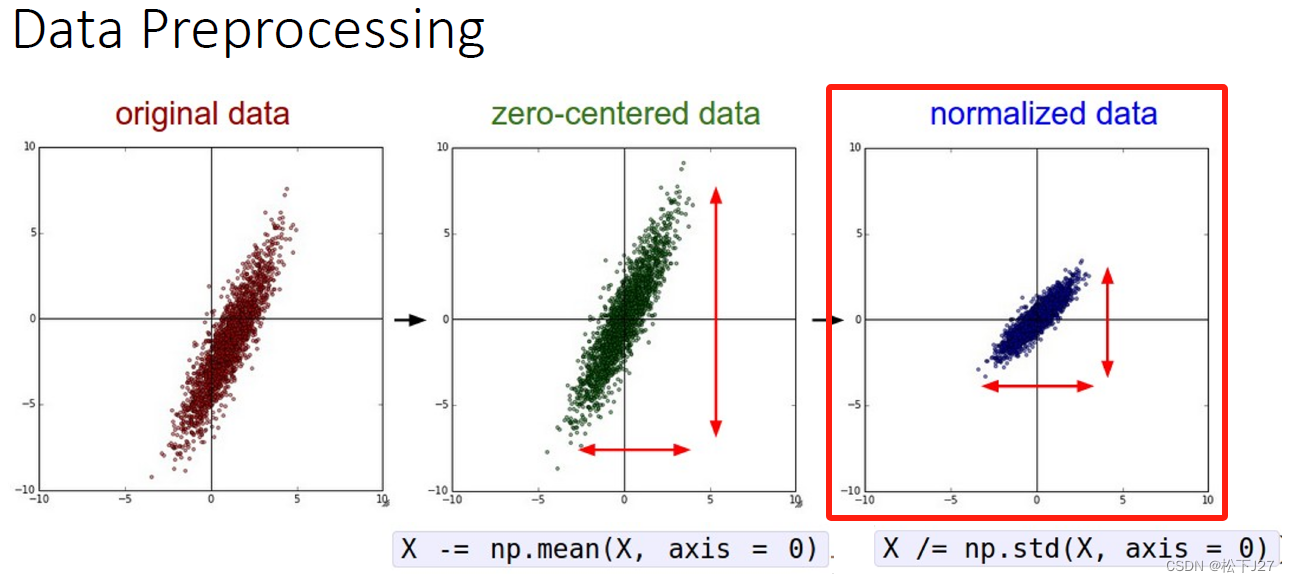
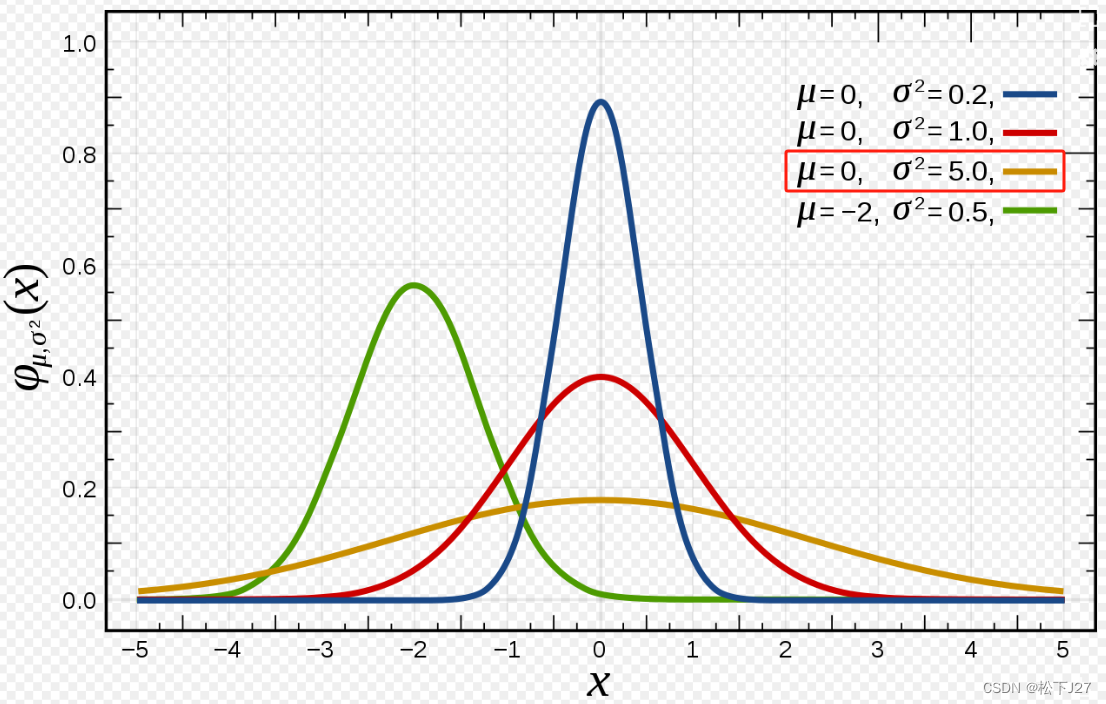
数据的标准化这个词比较难理解,从统计学的角度讲,经过这一步的处理,原始数据的标准差会变为1。换句话说,我的个人理解是如果原始数据分散的比较开,也就是高斯曲线的sigma比较大,则经过这一步处理后,分散的比较开的数据会被拉拢回来。比如说下图黄色曲线的数据分布。
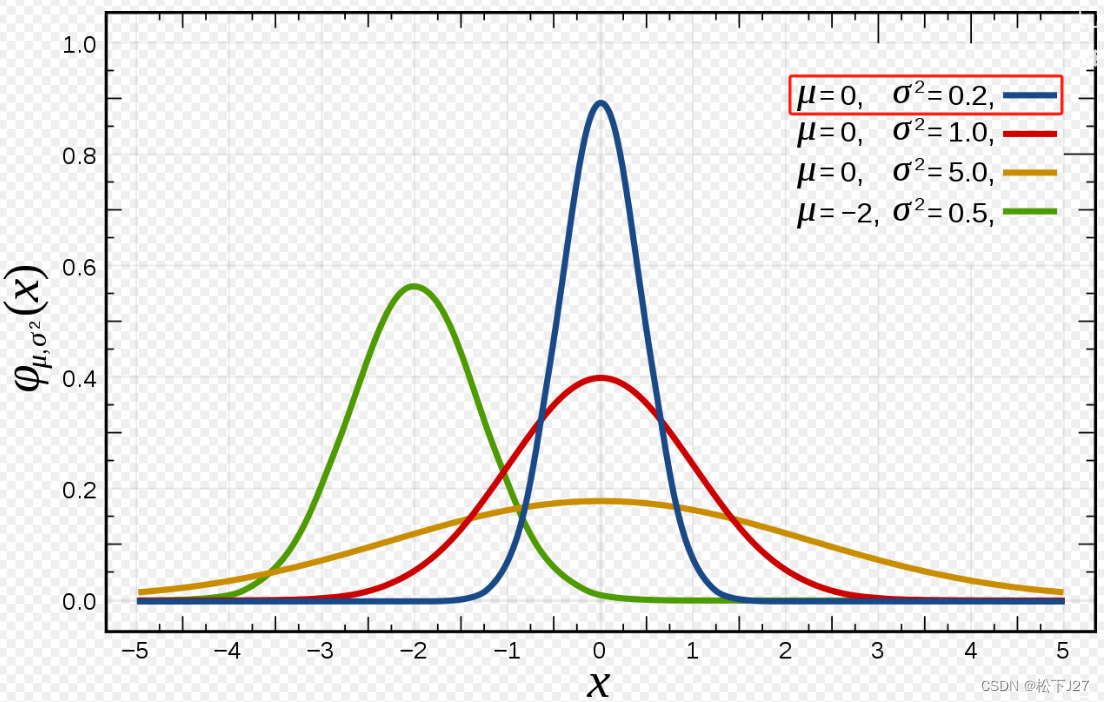
如果,原始数据本来分布的就过于集中,经过这一步处理后,数据反而会变的相对松散。例如下图蓝色曲线的数据分布。
数据的零点中心化和标准化是神经网络的数据预处理中最为常见的两个方法。可以用公式总结为:
其中,mean表示均值,sigma表示标准差。下面我通过两个例子看看这一过程究竟发生了什么。
2,3 以一维数据为例:
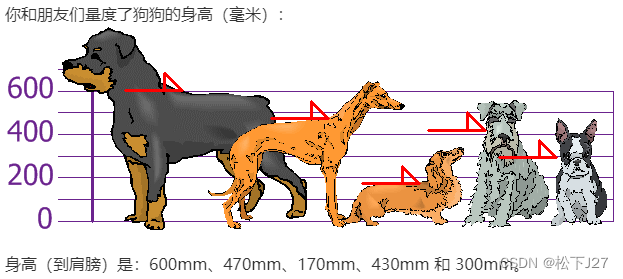
下图是我在jupyter notebook中所画的5个狗狗身高的一维数据集。x表示的是样本数,y表示的是该样本的高度。
import numpy as np
import matplotlib.pyplot as plt
data = [600,470,170,430,300]
num=len(data)
x=np.arange(num)
plt.figure()
plt.stem(x,data,label='dog(mm)')
plt.legend()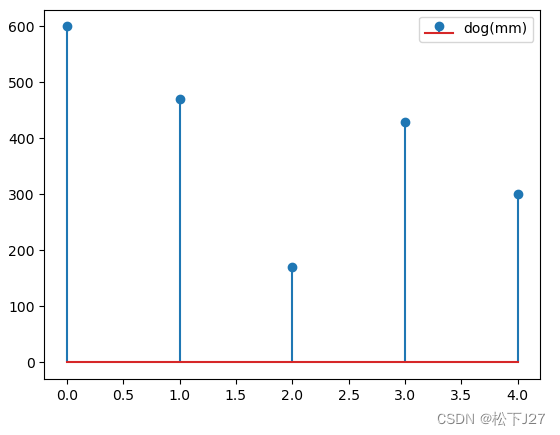
分别求出这组数据的mean和sigma并在图中表示出来
print('data=',data)
mean_data=np.mean(data)
print('mean=',mean_data)
sigma_data=np.std(data)
print('sigma=',sigma_data)
plt.figure
plt.stem(x,data,label='dog(mm)')
plt.plot(x,[mean_data]*num,'r-',label='mean')
plt.plot(x,[mean_data+sigma_data]*num,'b--',label='mean+sigma')
plt.plot(x,[mean_data-sigma_data]*num,'b--',label='mean-sigma')
plt.legend(loc='upper right')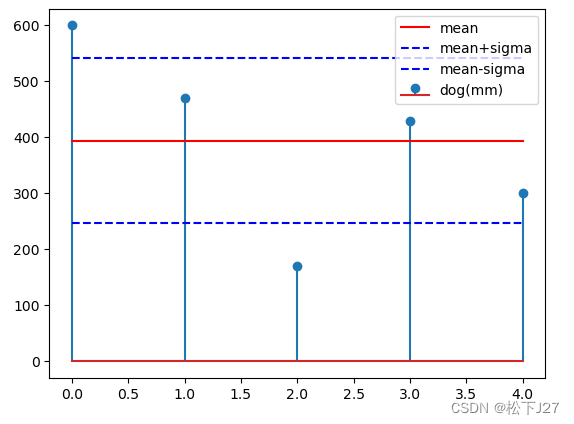
原始数据的直方图
plt.hist(data)
plt.title('Histogram of dog(mm)')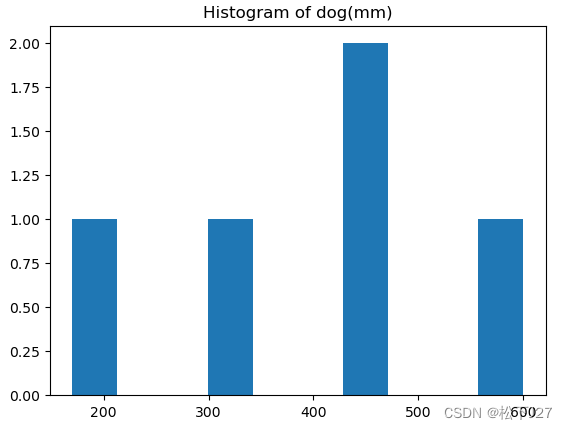
减去均值后的数据与直方图:
与原始数据相比减去均值后的数据均值为0,也就是说,原来以394mm为中心分布的数据变成了以0为中心分布的数据。
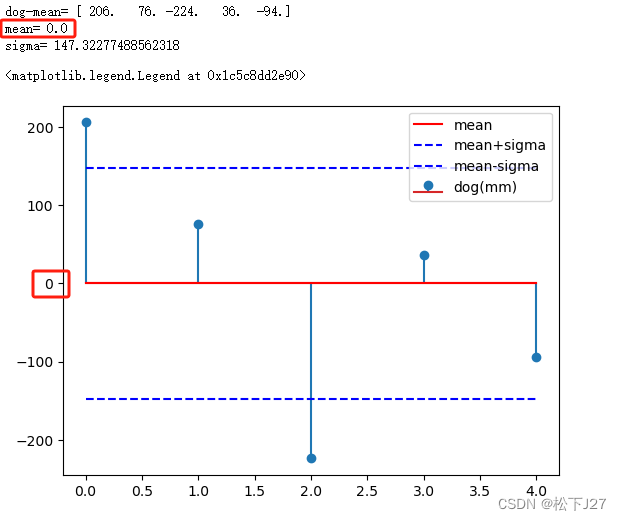
plt.hist(data1)
plt.title('Histogram of dog-mean (mm)')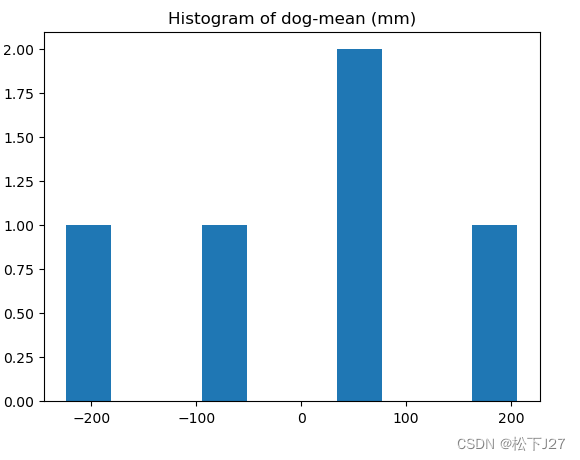
减去均值后再除以标准差后的数据及其分布:
除以标准差之后的数据,整个数据的标准差会变为1。这一变化在图像上会表现为数据的分布从原始状态中比较分散的情况,变成了比较集中的分布。
data2=data1/sigma_data
mean_data2=np.mean(data2)
sigma_data2=np.std(data2)
print('(dog-mean)/std=',data2)
print('mean=',mean_data2)
print('sigma=',sigma_data2)
plt.figure
plt.stem(x,data2,label='dog(mm)')
plt.plot(x,[mean_data2]*num,'r-',label='mean')
plt.plot(x,[mean_data2+sigma_data2]*num,'b--',label='mean+sigma')
plt.plot(x,[mean_data2-sigma_data2]*num,'b--',label='mean-sigma')
plt.legend(loc='upper right')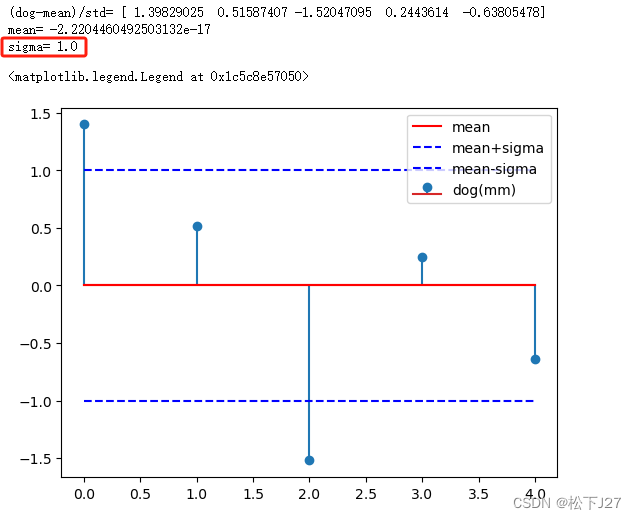
plt.hist(data2)
plt.title('Histogram of (dog-mean)/std (mm)')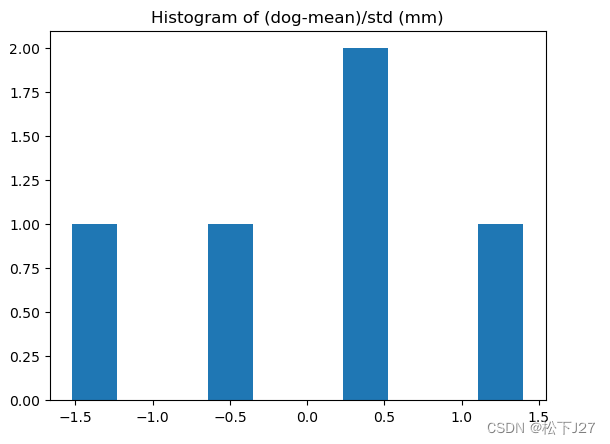
小结:
综合来看,原始数据经过这两步处理后变成了均值为0,标准差为1的数据。这也就是说,任何数据,只要经过减去均值和除以标准差这两步处理,都会强行变成一个标准正态分布。
2,4 以二维鸢尾花数据集数据为例:
原始数据:
from sklearn.datasets import load_iris
# 加载 Iris 数据集
iris = load_iris()
X = iris.data[:, :2] # 只取前两个特征作为示例
print('X.size=',X.shape)
y = iris.target
# 绘制散点图
fig,ax=plt.subplots(figsize=(8, 6))
scatter = ax.scatter(X[:, 0], X[:, 1], c=y, cmap='viridis', s=50, alpha=0.8, edgecolors='k')
plt.title('Scatter Plot of Iris Dataset')
plt.xlabel('x=Sepal Length (cm)')
plt.ylabel('y=Sepal Width (cm)')
plt.colorbar(scatter, label='Species', ticks=[0, 1, 2], format=lambda i, _: iris.target_names[int(i)])
# 绘制 x 轴和 y 轴
ax.axhline(0, color='black', linewidth=3) # 绘制水平的 x 轴
ax.axvline(0, color='black', linewidth=3) # 绘制垂直的 y 轴
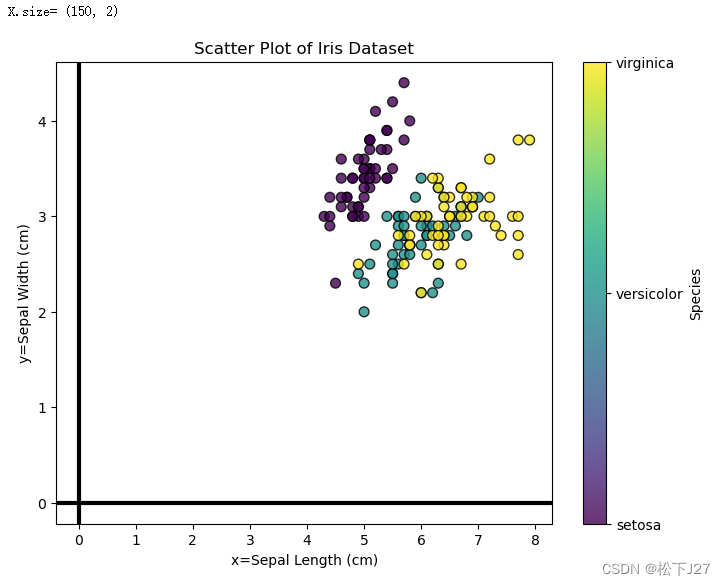
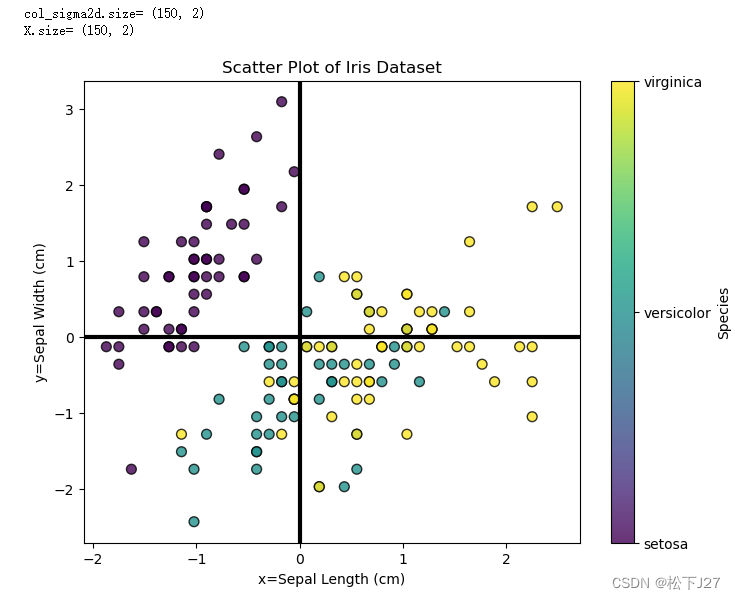
plt.show()在二维坐标系中,x轴和y轴分别表示鸢尾花花瓣的长度和宽度,各150个数据。 注意,此时的数据分布是偏离原点的。
plt.hist(X)
plt.title('Histogram of x,y(cm)')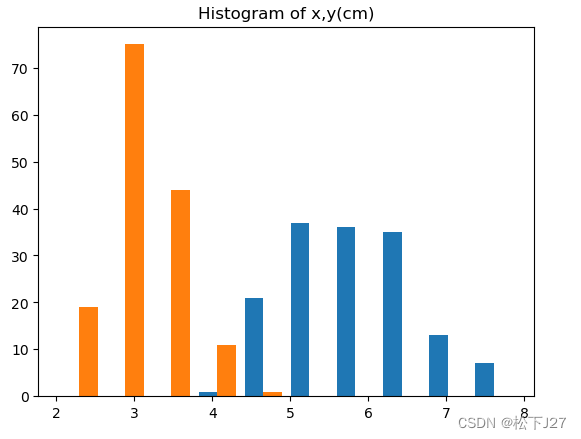
分别计算两个维度的mean和std:
col_avg=np.mean(X,axis=0)
print('col_avg.size=',col_avg.shape)
print('x_avg=',col_avg[0],'(cm)')
print('y_avg=',col_avg[1],'(cm)')
col_sigma=np.std(X,axis=0)
print('col_sigma.size=',col_sigma.shape)
print('x_sigma=',col_sigma[0],'(cm)')
print('y_sigma=',col_sigma[1],'(cm)')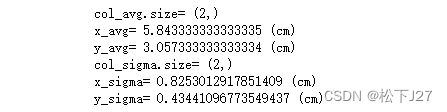
x,y两个维度的数据各自减去其均值:
先按列求各个维度的均值,然后让各自维度的数据减去各自维度的均值。
#reshape con_avg
col_avg2d=np.tile(col_avg,(X.shape[0],1))
print('col_avg2d.size=',col_avg2d.shape)
X-=col_avg2d
print('X.size=',X.shape)
# 绘制散点图
fig,ax=plt.subplots(figsize=(8, 6))
scatter = ax.scatter(X[:, 0], X[:, 1], c=y, cmap='viridis', s=50, alpha=0.8, edgecolors='k')
plt.title('Scatter Plot of Iris Dataset')
plt.xlabel('x=Sepal Length (cm)')
plt.ylabel('y=Sepal Width (cm)')
plt.colorbar(scatter, label='Species', ticks=[0, 1, 2], format=lambda i, _: iris.target_names[int(i)])
# 绘制 x 轴和 y 轴
ax.axhline(0, color='black', linewidth=3) # 绘制水平的 x 轴
ax.axvline(0, color='black', linewidth=3) # 绘制垂直的 y 轴
plt.show()减去均值后的数据分布是以原点为中心的。
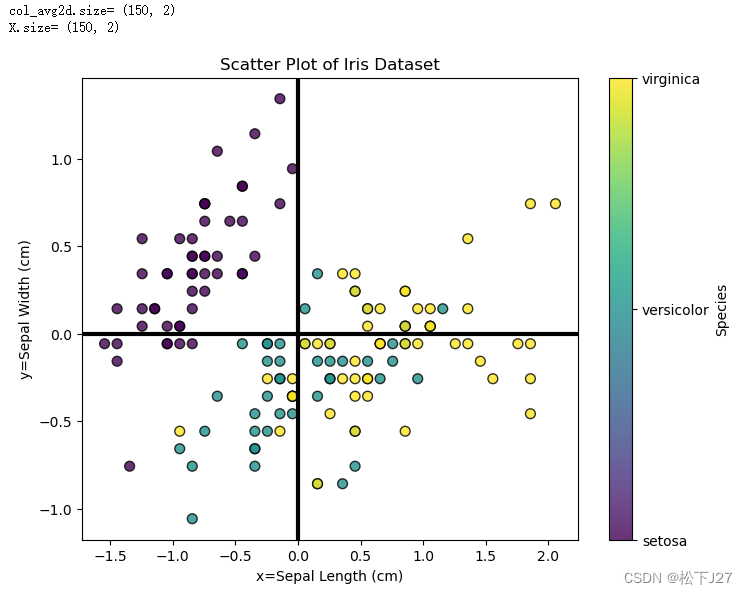
plt.hist(X)
plt.title('Histogram of x,y(cm)')在直方图中也可以看到新的数据集是以0为中心的。
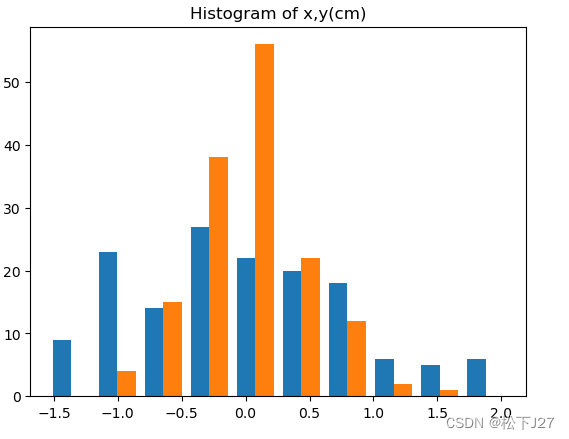
两个维度分别除以各自维度的标准差:
#reshape con_sigma
col_sigma2d=np.tile(col_sigma,(X.shape[0],1))
print('col_sigma2d.size=',col_sigma2d.shape)
X/=col_sigma2d
print('X.size=',X.shape)
# 绘制散点图
fig,ax=plt.subplots(figsize=(8, 6))
scatter = ax.scatter(X[:, 0], X[:, 1], c=y, cmap='viridis', s=50, alpha=0.8, edgecolors='k')
plt.title('Scatter Plot of Iris Dataset')
plt.xlabel('x=Sepal Length (cm)')
plt.ylabel('y=Sepal Width (cm)')
plt.colorbar(scatter, label='Species', ticks=[0, 1, 2], format=lambda i, _: iris.target_names[int(i)])
# 绘制 x 轴和 y 轴
ax.axhline(0, color='black', linewidth=3) # 绘制水平的 x 轴
ax.axvline(0, color='black', linewidth=3) # 绘制垂直的 y 轴
plt.show()如果原始数据分布的较为集中(即,标准差<1),除以标准差之后数据的分布会变得相对松散。如果原始数据分布的较为分散(即,标准差>1),除以标准差之后数据的分布会变得相对集中。
col_avg=np.mean(X,axis=0)
print('col_avg.size=',col_avg.shape)
print('x_avg=',col_avg[0],'(cm)')
print('y_avg=',col_avg[1],'(cm)')
col_sigma=np.std(X,axis=0)
print('col_sigma.size=',col_sigma.shape)
print('x_sigma=',col_sigma[0],'(cm)')
print('y_sigma=',col_sigma[1],'(cm)')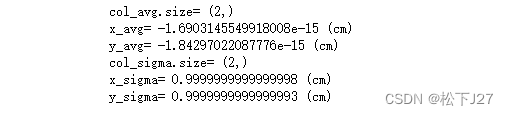
经过预处理后的数据,均值为0,标准差为1.
plt.hist(X)
plt.title('Histogram of x,y(cm)')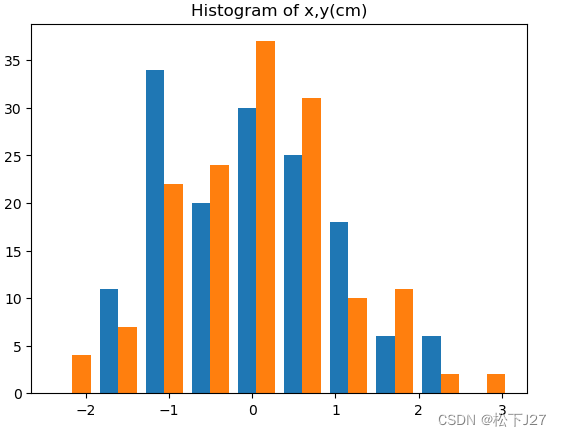
2,5 在实际应用中数据预处理的常用方法

(全文完)
--- 作者,松下J27
参考文献(鸣谢):
1,Stanford University CS231n: Deep Learning for Computer Vision
2,训练神经网络(第一部分)_哔哩哔哩_bilibili
3,10 Training Neural Networks I_哔哩哔哩_bilibili
4,Schedule | EECS 498-007 / 598-005: Deep Learning for Computer Vision
5,标准差和方差
版权声明:所有的笔记,可能来自很多不同的网站和说明,在此没法一一列出,如有侵权,请告知,立即删除。欢迎大家转载,但是,如果有人引用或者COPY我的文章,必须在你的文章中注明你所使用的图片或者文字来自于我的文章,否则,侵权必究。 ----松下J27