文章目录
- 一、文章概览
- (一)问题的提出
- (二)文章工作
- 二、理论背景
- (一)密度比估计DRE
- (二)去噪扩散模型
- 三、方法
- (一)推导分类和去噪之间的关系
- (二)组合训练方法
- (三)一步精确的似然计算
- 四、实验
- (一)使用两种损失对于实现最佳分类器的重要性
- (二)去噪结果、图像质量和负对数似然
论文:Classification Diffusion Models: Revitalizing Density Ratio Estimation
一、文章概览
(一)问题的提出
学习数据分布的重要方法:密度比估计(DRE)
- 密度比估计训练模型以在数据样本和来自某个参考分布的样本之间进行分类。
- 优势:基于 DRE 的模型可以直接输出任何给定输入的可能性,这是大多数生成技术所缺乏的非常理想的属性
- 劣势:DRE 方法一直难以准确捕获图像等复杂高维数据的分布
复杂高维数据的生成建模:去噪扩散模型(DDM)
- 优势:可以处理复杂高维数据的生成建模问题,应用于解决逆问题、图像编辑和医学数据增强
- 劣势:评估数据样本的可能性是一项具有挑战性的任务,需要许多神经函数评估(NFE)来计算可能性 - ELBO,或使用 ODE 求解器来近似精确的可能性。
(二)文章工作
提出分类扩散模型(CDM):基于DRE的生成方法
- 采用去噪扩散模型(DDM)的形式
- 利用分类器来预测添加到干净信号中的噪声水平
- 将预测添加到数据样本中的高斯白噪声水平的最佳分类器与清除这种噪声的 MMSE 降噪器之间建立了连接
- DDMs依赖于最小均方误差(MMSE)去噪
- DRE方法则依赖于最优分类
二、理论背景
(一)密度比估计DRE
噪声对比估计(NCE)方法:
-
从最优二元分类器中提取未知分布 p d ( x ) p_d(x) pd(x) 和已知参考分布 p n ( x ) p_n(x) pn(x) 之间的比率,以区分 p d ( x ) p_d(x) pd(x) 和 p n ( x ) p_n( x) pn(x)。一旦从分类器中提取出该比率,就可以将其乘以已知的 p n ( x ) p_n(x) pn(x) 以获得 p d ( x ) p_d(x) pd(x)。
-
具体来说,令 C C C表示样本 x x x的类别,其中 C C C = 1、0分别对应于 x x x 是来自 p d ( x ) p_d(x) pd(x)、 p n ( x ) p_n(x) pn(x)的样本的事件。从 x x x 预测 C C C 的最佳分类器输出 P ( C = 1 ∣ x ) P(C = 1|x) P(C=1∣x) 和 P ( C = 0 ∣ x ) P(C = 0|x) P(C=0∣x)。使用贝叶斯规则可以计算密度比
p d ( x ) p n ( x ) = P ( C = 1 ∣ x ) P ( C = 0 ∣ x ) \frac{p_d(x)}{p_n(x)}=\frac{P(C=1|x)}{P(C=0|x)} pn(x)pd(x)=P(C=0∣x)P(C=1∣x)
DRE的密度断层问题:
当目标分布
p
d
(
x
)
p_d(x)
pd(x) 和已知参考分布
p
n
(
x
)
p_n(x)
pn(x)差异显著时,传统的密度比估计(DRE)方法可能会失败。因为当训练一个分类器来区分图像和噪声时,分类器可以在不学习有关图像的有意义信息的情况下达到高精度。一旦分类器达到这一点,其权重实际上会停止更新。
TRE方法:
使用一系列列逐渐接近的分布
p
x
0
(
x
)
,
p
x
1
(
x
)
,
.
.
.
,
p
x
m
(
x
)
p_{x0}(x),p_{x1}(x),...,p_{xm}(x)
px0(x),px1(x),...,pxm(x),其中
p
x
m
(
x
)
p_{xm}(x)
pxm(x)是参考分布,而
p
x
0
(
x
)
p_{x0}(x)
px0(x)是目标分布。中间的分布
{
p
x
i
(
x
)
}
i
=
1
m
−
1
\{p_{xi}(x)\}_{i=1}^{m-1}
{pxi(x)}i=1m−1不需要事先知道具体形式,只要能够从中采样即可。
- 定义 p x i ( x ) p_{xi}(x) pxi(x)为 x i = α ˉ i x 0 + 1 − α ˉ i x m x_i=\sqrt{\bar{\alpha}_i}x_0+\sqrt{1-\bar{\alpha}_i}x_m xi=αˉix0+1−αˉixm,其中 x 0 ∼ p x 0 , x m ∼ p x m x_0\sim p_{x0},x_m\sim p_{xm} x0∼px0,xm∼pxm, α ˉ i \bar{\alpha}_i αˉi是一个从1逐渐减少到0的序列;
- 利用密度比估计的原理,可以通过训练二元分类器来区分来自 p x i ( x ) p_{xi}(x) pxi(x)和 p x i + 1 ( x ) p_{xi+1}(x) pxi+1(x)的样本,提取每对相邻分布 p x i ( x ) / p x i + 1 ( x ) p_{xi}(x)/p_{xi+1}(x) pxi(x)/pxi+1(x)的比值;
- 计算出目标分布和参考分布之间的比值:
p x 0 ( x ) p x m ( x ) = p x 0 ( x ) p x 1 ( x ) ⋅ p x 1 ( x ) p x 2 ( x ) ⋅ . . . ⋅ p x m − 2 ( x ) p x m − 1 ( x ) ⋅ p x m − 1 ( x ) p x m ( x ) \frac{p_{x0}(x)}{p_{xm}(x)}=\frac{p_{x0}(x)}{p_{x1}(x)}\cdot \frac{p_{x1}(x)}{p_{x2}(x)}\cdot ... \cdot \frac{p_{xm-2}(x)}{p_{xm-1}(x)}\cdot \frac{p_{xm-1}(x)}{p_{xm}(x)} pxm(x)px0(x)=px1(x)px0(x)⋅px2(x)px1(x)⋅...⋅pxm−1(x)pxm−2(x)⋅pxm(x)pxm−1(x)
优点:通过这种方法,TRE方法通过增加分类任务的复杂度,使得DRE方法能够有效地估计复杂的目标分布 ,而不会受到传统方法中密度断层问题的限制。
缺点:TRE方法中的每个比值 p x i ( x ) p x i + 1 ( x ) \frac{p_{xi}(x)}{p_{xi+1}(x)} pxi+1(x)pxi(x)都是从仅在分布 p x i p_{xi} pxi和 p x i + 1 p_{xi+1} pxi+1上训练的二元分类器中提取出来的,也就是说不同比值是从不同分布上得到的,这可能导致训练和推断时出现不匹配,因为在推断时,所有的比值都是在相同的输入x上评估的。

(二)去噪扩散模型
【论文精读】DDPM:Denoising Diffusion Probabilistic Models 去噪扩散概率模型
DDM作为一个最小均方误差(MMSE)去噪器,其行为受噪声水平条件影响;而CDM则作为一个分类器。对于给定的噪声图像,CDM输出一个概率向量,预测噪声水平。这个概率向量中的第 t t t 个元素表示输入图像的噪声水平对应于扩散过程中的第 t t t 个时间步的概率。CDM可以用来输出MMSE去噪后的图像,方法是根据我们在定理3.1中展示的内容,计算其输出概率向量关于输入图像的梯度。
换句话说,CDM通过输出的概率向量,可以反向推导出输入图像在不同噪声水平下的最小均方误差去噪结果。

三、方法
(一)推导分类和去噪之间的关系
我们首先推导出分类和去噪之间的关系,然后将其用作我们的 CDM 方法的基础。
随机向量 x t x_t xt包含了时间步 t ∈ { 1 , . . . , T } t\in \{1,...,T\} t∈{1,...,T},并设置0和 T + 1 T+1 T+1两个额外的时间步,分别对应干净图像和纯高斯噪声。具体地,定义 α ˉ 0 = 1 \bar{\alpha}_0=1 αˉ0=1 和 α ˉ T + 1 = 0 \bar{\alpha}_{T+1}=0 αˉT+1=0 。每个时刻 t t t随机向量 x t x_t xt的密度为 p x t ( x ) p_{x_t}(x) pxt(x)。
分类器的输出:
文章方法的核心是训练一个分类器,接受一个噪声样本
x
t
x_t
xt,并预测其所在的时刻
t
t
t。形式上,假设
t
t
t是一个取值在
{
0
,
,
1
,
.
.
.
,
T
,
T
+
1
}
\{0,,1,...,T,T+1\}
{0,,1,...,T,T+1}的离散随机变量,概率质量函数为
p
t
(
t
)
=
P
(
t
=
t
)
p_t(t)=P(t=t)
pt(t)=P(t=t),并且随机向量
x
~
\tilde{x}
x~是在随机时刻
t
t
t的扩散信号,即
x
~
=
x
t
\tilde{x}=x_t
x~=xt。注意到每个
x
t
x_t
xt的密度可以写成
p
x
t
(
x
)
=
p
x
~
∣
t
(
x
∣
t
)
p_{x_t}(x)=p_{\tilde{x}|t}(x|t)
pxt(x)=px~∣t(x∣t),根据全概率公式,
x
~
\tilde{x}
x~的密度为:
p
x
~
(
x
)
=
∑
t
=
1
T
+
1
p
x
t
(
x
)
p
t
(
t
)
p_{\tilde{x}}(x)=\sum_{t=1}^{T+1}p_{x_t}(x)p_t(t)
px~(x)=t=1∑T+1pxt(x)pt(t)
给定从 p x ~ ( x ) p_{\tilde{x}}(x) px~(x)抽样的样本 x x x,我们感兴趣的是一个分类器,输出概率向量 ( p t ∣ x ~ ( 0 ∣ x ) , p t ∣ x ~ ( 1 ∣ x ) . . . , p t ∣ x ~ ( T + 1 ∣ x ) ) (p_{t|\tilde{x}}(0|x),p_{t|\tilde{x}}(1|x)...,p_{t|\tilde{x}}(T+1|x)) (pt∣x~(0∣x),pt∣x~(1∣x)...,pt∣x~(T+1∣x)),其中 p t ∣ x ~ ( t ∣ x ) = P ( t = t ∣ x ~ = x ) p_{t|\tilde{x}}(t|x)=P(t=t|\tilde{x}=x) pt∣x~(t∣x)=P(t=t∣x~=x)。
分类器的梯度就是DDM中的去噪器:
假设我们有一个去噪器,其作用是去除样本中的噪声,这个去噪器可以看作是对分类器输出的概率向量的梯度操作。通过这个梯度操作,我们可以得到每个时间步对应的去噪后的结果。公式表达为:
令
F
(
x
,
t
)
=
log
(
p
t
∣
x
~
(
T
+
1
∣
x
)
)
−
log
(
p
t
∣
x
~
(
t
∣
x
)
)
F(x,t)=\log(p_{t|\tilde{x}}(T+1|x))-\log(p_{t|\tilde{x}}(t|x))
F(x,t)=log(pt∣x~(T+1∣x))−log(pt∣x~(t∣x)),则有:
E
(
ϵ
t
∣
x
t
=
x
t
)
=
1
−
α
ˉ
t
(
∇
x
t
F
(
x
t
,
t
)
+
x
t
)
E(\epsilon_t|x_t=x_t)=\sqrt{1-\bar{\alpha}_t}(\nabla_{x_t}F(x_t,t)+x_t)
E(ϵt∣xt=xt)=1−αˉt(∇xtF(xt,t)+xt)
使用标准交叉熵(CE)损失简单地训练这样的分类器会导致糟糕的结果:
因此,我们可以训练一个分类器,并根据上述公式使用其梯度作为降噪器,然后应用任何所需的采样方法(例如DDPM、DDIM等)。然而,使用标准交叉熵(CE)损失简单地训练这样的分类器会导致糟糕的结果。这是因为即使没有学习到任何时间步
t
t
t下正确的概率
p
t
∣
x
~
(
t
∣
x
)
p_{t|\tilde{x}}(t|x)
pt∣x~(t∣x),分类器也可能达到较低的 CE 损失。 这种现象可以在下图中观察到,它说明了迄今为止 DRE 方法未能捕获图像等高维复杂数据的分布的原因。

(二)组合训练方法
为了获得任何时间步
t
t
t下正确的概率
p
t
∣
x
~
(
t
∣
x
)
p_{t|\tilde{x}}(t|x)
pt∣x~(t∣x),我们建议使用一种结合了分类器输出的交叉熵损失和其梯度的均方误差的训练方法。完整训练算法如算法1所示:

算法 2 展示了如何使用 DDPM 采样器通过 CDM 生成样本,而类似的方法也可用于其他采样器。使用 CDM 的 DDPM 采样中的每个步骤 t 由下式给出:
x
t
−
1
=
α
t
x
t
−
1
−
α
t
α
t
∇
x
t
F
θ
(
x
t
,
t
)
+
σ
t
z
x_{t-1}=\sqrt{\alpha_t}x_t-\frac{1-\alpha_t}{\sqrt{\alpha_t}}\nabla_{x_t}F_\theta(x_t,t)+\sigma_tz
xt−1=αtxt−αt1−αt∇xtFθ(xt,t)+σtz
(三)一步精确的似然计算
为了计算给定样本的似然,DDM 需要多次评估神经网络来使用诸如证据下界(ELBO)或者基于ODE求解器来近似对数似然的方法,作为基于DRE的方法,Classifier-Defined Models(CDMs)具有显著优势。CDMs可以在单次神经网络评估(NFE)中计算精确的似然性。具体地,对于任意所需的时间步长t,CDMs可以计算与噪声图像分布 p x t p_{xt} pxt相关的精确似然性。
对于任意
t
∈
{
0
,
1
,
.
.
,
T
+
1
}
t\in \{0,1,..,T+1\}
t∈{0,1,..,T+1},有:
p
x
t
(
x
)
=
p
t
(
T
+
1
)
p
t
(
t
)
p
t
∣
x
~
(
t
∣
x
)
p
t
∣
x
~
(
T
+
1
∣
x
)
N
(
x
;
0
,
I
)
p_{x_t}(x)=\frac{p_t(T+1)}{p_t(t)}\frac{p_{t|\tilde{x}}(t|x)}{p_{t|\tilde{x}}(T+1|x)}\mathcal{N}(x;0,\mathcal{I})
pxt(x)=pt(t)pt(T+1)pt∣x~(T+1∣x)pt∣x~(t∣x)N(x;0,I)
- 第一项仅取决于预先选择的概率质量函数 p t p_t pt(在我们的实验中选择为均匀分布)
- 第二项可以从分类器输出向量的第 t t t 和 T + 1 T+1 T+1 个条目中获得。这意味着我们可以计算任何给定图像 x x x相对于任意噪声水平 t t t 下的噪声图像密度 p x t p_{xt} pxt 的似然性。
四、实验
(一)使用两种损失对于实现最佳分类器的重要性
使用不同损失训练的模型达到的MSE、CE和分类准确率:从表格 1 可以明显看出,仅使用CE损失时,MSE很高;而仅使用MSE损失时,CE和分类准确率则很差。一个重要的观察点是,即使在使用CE损失训练时,分类器的准确率也很低。这是使得DRE方法有效的关键前提。具体来说,为了避免密度差问题,分类问题应该足够困难,否则分类器甚至可以在没有学习到正确密度比率的情况下轻松区分类别。

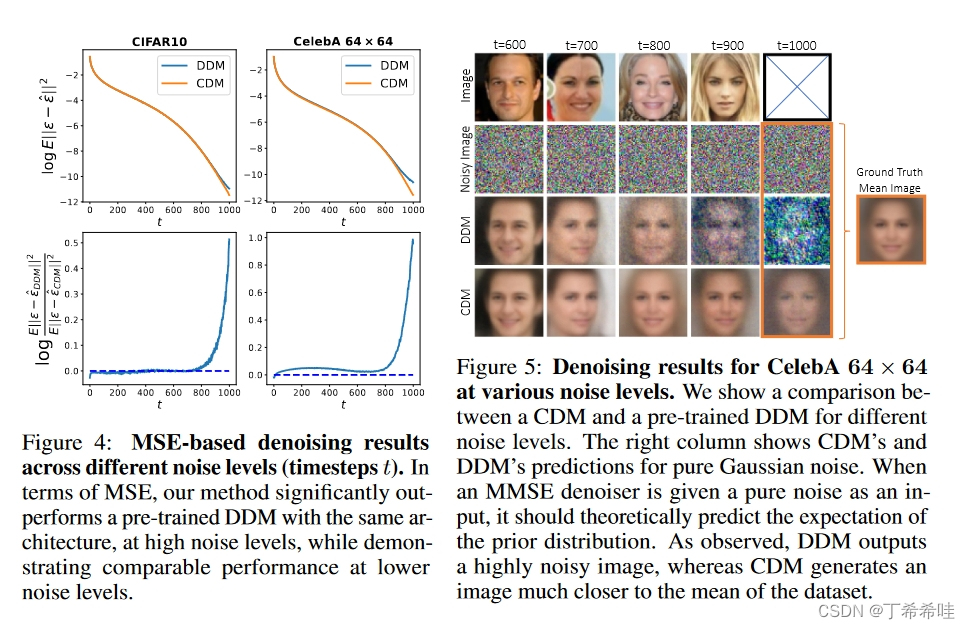
(二)去噪结果、图像质量和负对数似然
对于图像去噪,CDM 在 MSE 方面超过了高噪声水平下预训练的 DDM,同时在较低噪声水平下实现了可比较的 MSE,如图 4 所示。这些定量结果得到了图 5 中的定性示例的证实,它展示了不同噪声水平下的图像去噪结果。