简介

为什么会写这篇文章？
因为鄙人刷过此题多次，每次觉得自己会了，可下次还是不能一下子写出题解，故记录下我是如何记忆此题的，并且探索一些编程理念。

题目

一只青蛙一次可以跳上1级台阶，也可以跳上2级。求该青蛙跳上一个 n 级的台阶总共有多少种跳法（先后次序不同算不同的结果）。
数据范围：
1≤𝑛≤40 1≤n≤40
要求：时间复杂度：𝑂(𝑛)，空间复杂度： 𝑂(1)

解法

这个题有 递归（自上而下） 和 动态规划（自下而上） 两种解法。
两种解法都可以参考此图（树）：

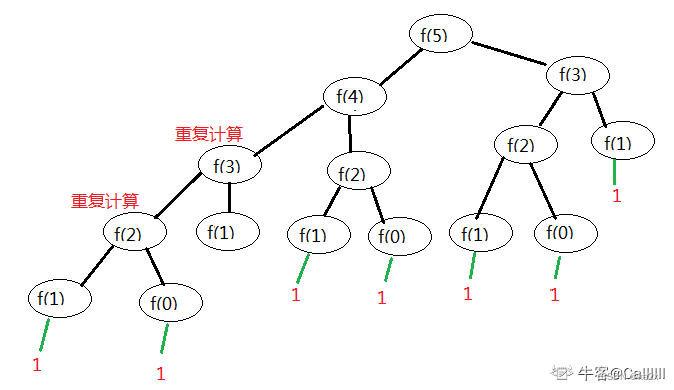
f(n) ：计算跳到第n个台阶的跳法数量。
跳到n，肯定是从第“n-1”或“n-2”个台阶跳过来的，也就是 f(n)=f(n-1)+f(n-2)。
递归（自上而下）会重复计算。而动态规划（自下而上）则可以在计算的过程中保存 “跳到较低台阶的跳法数量” 的计算结果。
当然极限情况要考虑好，也就是 f(0) 和 f(1) 是我们要考虑的， f(0) = 1是因为跳到第0个台阶的跳法数量=1，如果不好理解，也可以从f(2)=f(1)+f(0) 来理解f(0)为什么等于1。
而动态规划（自下而上）则可以先计算 f(2) = f(1) + f(0)，再计算 f(3) = f(2) + f(1)、f(4) … f(n) ，每次计算保存至少最后两个计算结果，有最后两个计算结果，即可计算出再下一个结果。

相关代码：

递归解法：

int jumpFloor(int number) {
        if (number<=1) return 1;
        return jumpFloor(number-1)+jumpFloor(number-2);
   }

动态规划：

  public int jumpFloor (int number) {
      // a保存n-2，b保存n-1，c保存n
      int a = 1 , b = 1 , c = 1;
      for (int i = 2 ; i <= number ; i ++) {
          c = a + b;
          a = b;
          b = c;
      }
      return c;
  }

代码不唯一，思想对了，代码持续用用例来debug也能写出来。