临床预测模型,也是临床统计分析的一个大类,除了前期构建模型,还要对模型的预测能力、区分度、校准度、临床获益等方面展开评价,确保模型是有效的!
其中评价模型的好坏主要方面还是要看区分度和校准度,而区分度方面目前最常见的是ROC曲线(Receiver Operating Characteristic,中文名字叫“受试者工作特征曲线”),由灵敏度为纵轴,(1-特异度)为横轴绘制而成,用于评价X(检验变量)对于Y(状态变量)的预测准确率情况。越靠左上方,说明模型的预测准确性越好,可以让读者直观地看到某指标各取值对结局指标的诊断或预测能力。
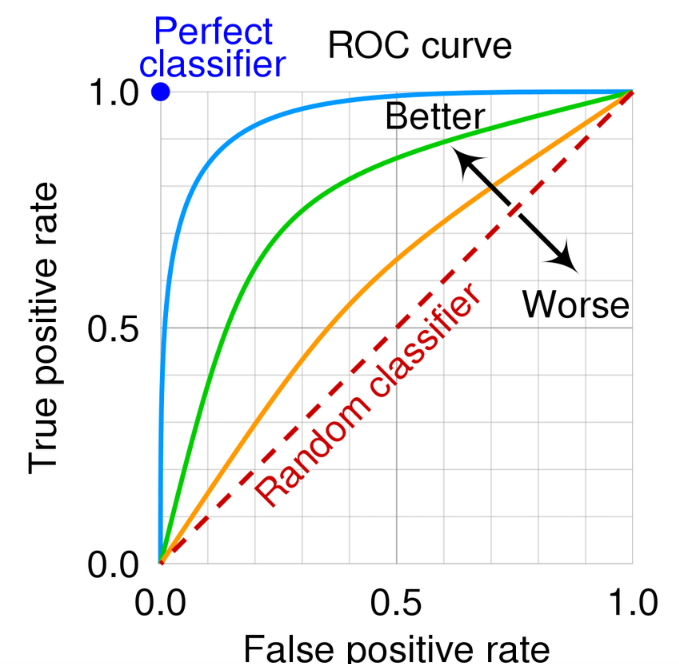
此外,ROC曲线还会使用曲线下面积(AUC)的大小对模型进行评价,AUC的取值范围为0.5到1之间,曲线下面积越大,越接近于1,模型的诊断或预测效果越好:
AUC在0.9以上时,准确性较高
在0.7~0.9时,有一定准确性
AUC在 0.5~0.7时,准确性较低
AUC=0.5时,说明诊断方法完全不起作用,无诊断价值。
AUC<0.5不符合真实情况,在实际中极少出现
理论知识比较好理解,但是实际分析中,想要绘制出精美的ROC曲线,还要花一番功夫,像是常见的R语言软件就需要大量参数进行调整,并且训练集和验证集图像还需要分开绘制两遍......
因此,这里为大家推荐一个统计分析小工具——风暴统计,可以超快速绘制完成临床预测模型的ROC曲线,一次性给出训练集与验证集的图像!
风暴统计是由浙江中医药大学的郑卫军教授基于R语言开发的,不仅结果准确性有保障,并且全部实现菜单化操作,统计小白也可以轻松上手,绘制精美的ROC曲线!
下面我们就结合一份实操数据来为大家详细介绍一下具体的操作步骤吧!
实操具体网址:https://www.zstats.cn/software/logpre3/
或者百度、必应Bing搜索“风暴统计”
本平台上线的所有工具都是免费的

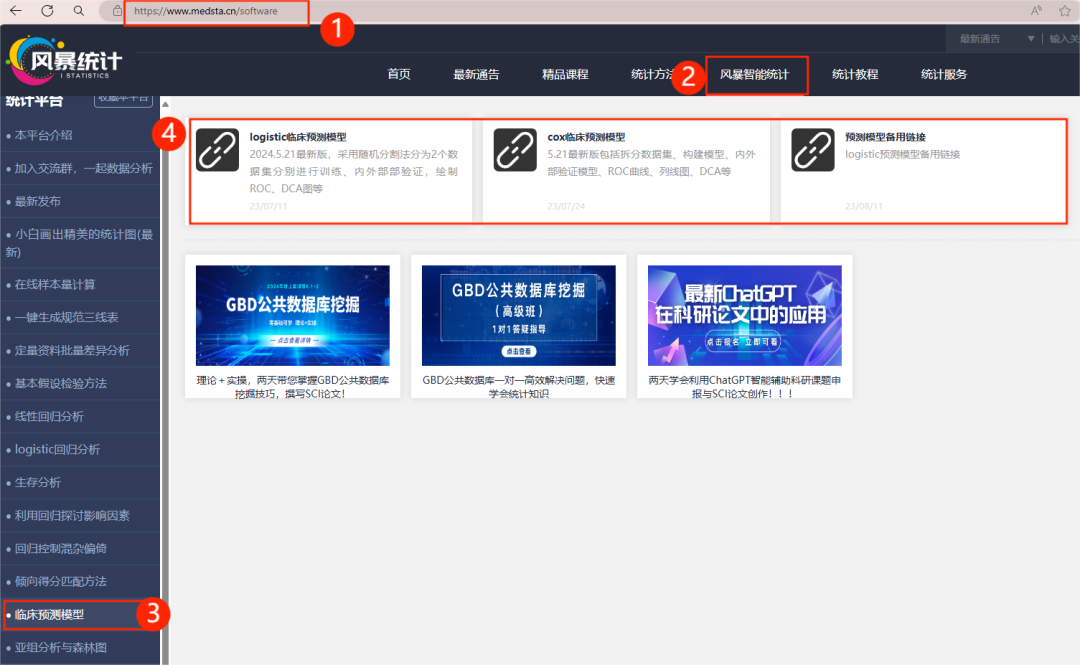
1.进入风暴统计平台
首先,浏览器搜索风暴统计,依次点击"风暴智能统计"——"临床预测模型"——"logistic临床预测模型"!进入分析界面后,根据提示,完成数据的导入与整理。
这里我们不再赘述数据的导入与整理过程,详细教程大家可以点击下方链接:
详细指南!风暴统计如何高效导入数据,统计分析快人一步?
详细版!如何利用风暴统计进行数据的整理转换?
2.数据集拆分
预测模型都需要内部验证,内部验证的方法有随即拆分、交叉验证、Boostrap等。但风暴统计平台目前仅能做随即拆分法内部验证。
随机拆分法内部验证,顾名思义就是将原始数据集按照7:3(常见)或者6:4等比例进行拆分,一部分用于建模,另外一部分用于验证模型。
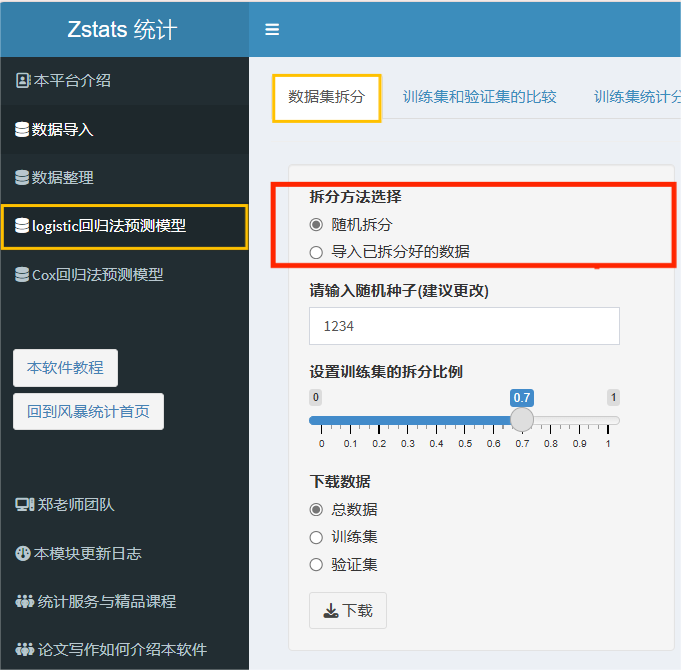
风暴统计支持两种拆分方式:随机拆分法、导入已拆分好的数据。
如果选择“随机拆分”,需要设置随机种子和拆分比例。随机种子对于数字位数没有要求,作用是可以保证拆分数据的分析结果可以复现,平台默认是1234,拆分比例更好理解,只需要拖动滑条,蓝色部分就是训练集的数据占总数据的比例。
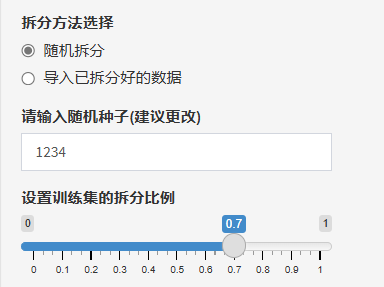
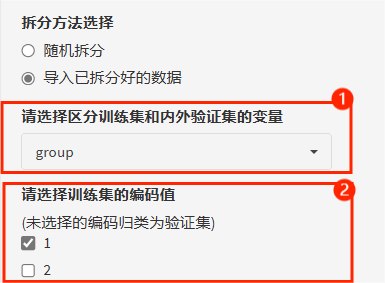
如果选择“导入已拆分好的数据”,需要设置事先在导入的数据集中增加一列用于区分训练集和验证集的变量,比如新增列叫"group",通过编码赋值1代表训练集,2代表验证集。那么第一步:选入区分训练集与验证集的变量,第二步:勾选代表训练集的编码值!
注:“导入已拆分好的数据”不仅可以做内部验证,更重要还可以用来做外部验证哦!同样需要一列变量来区分训练集和外部验证集!
3.构建预测模型
完成数据记得拆分后,我们就可以开始构建预测模型啦!请注意,预测模型的构建仅在训练集开展哦!
预测模型的本质,简单来说,也就是多因素回归模型!多因素回归听上去是不是平易近人许多?风暴统计可以超快速完成这一步!
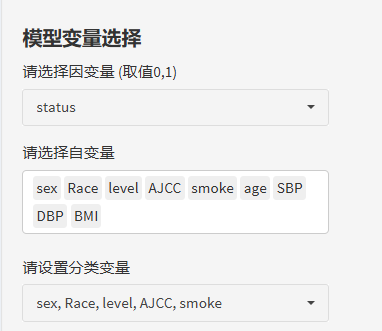
首先,选择模型变量——因变量、自变量。因变量必须是以0和1赋值的哦!自变量就可以放入我们数据中所有可能的预测因子!
接着,定义模型自变量筛选的方式,满足筛选条件的自变量会进入多因素回归模型!
注:多因素模型中的所有变量就是我们最终预测模型中全部的预测因子了,并不只是多因素中有意义的变量哦!如果希望预测模型中的变量P值均小于0.05,可以选择逐步回归分析中"根据P<0.05筛选"的选项!
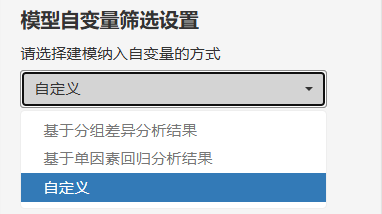
自变量筛选方式也有3种:
基于分组差异性结果:
基于单因素回归结果
自定义
前两个比较相似,区别就在是根据差异性P值还是单因素P值进行筛选!
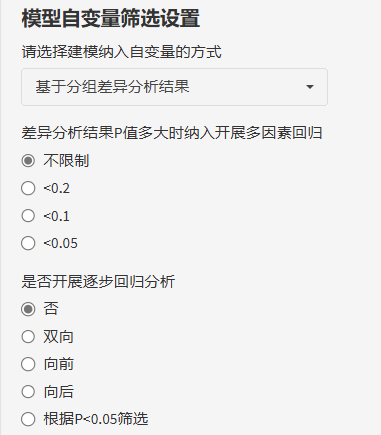
如果选择了"基于分组差异性"或"基于单因素回归",只需要完成2步设置。
第一步,P阈值的选择,如果自变量个数过少,可以适当放宽标准,0.1、0.2也都是可以的。当选择不限制时,单因素的全部自变量都将纳入多因素回归分析。
第二步,是否开展逐步回归,选择“否”,就是我们常见的先单后多分析,另外逐步回归方法,平台也提供了多种选择:双向逐步回归,向前逐步回归,向后逐步回归以及考虑到有时P值大于0.05的变量在逐步回归时也会留在模型中,新增了根据P<0.05的原则开展逐步回归!大家可以根据研究需要自行选择。
 |
|
如果选择了自定义筛选自变量,比如实际研究中,预测因子的筛选也需要结合专业知识以及相关文献进行判断,纯数据驱动也不太好。假如变量A在临床中是十分重要的变量,但是受限于样本原因,单因素与差异性均没有统计学意义,这时候,我们可以自定义挑选预测因子,选择我们预期的预测因子,自行选择是否需要逐步回归!也是一条途径!
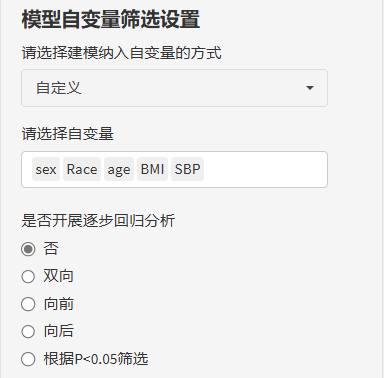
选择完毕后,我们就得到了多因素回归的结果,现在多因素模型也就是我们最终的预测模型,列线图中会包含多因素回归中的全部变量!

完成预测模型的构建后,就可以同步给出模型得到验证结果啦!
4.模型区分度评价
点击"ROC曲线与AUC面积"模块,结果也同时输出,包括有训练集ROC曲线、验证集ROC曲线、ROC曲线叠加。
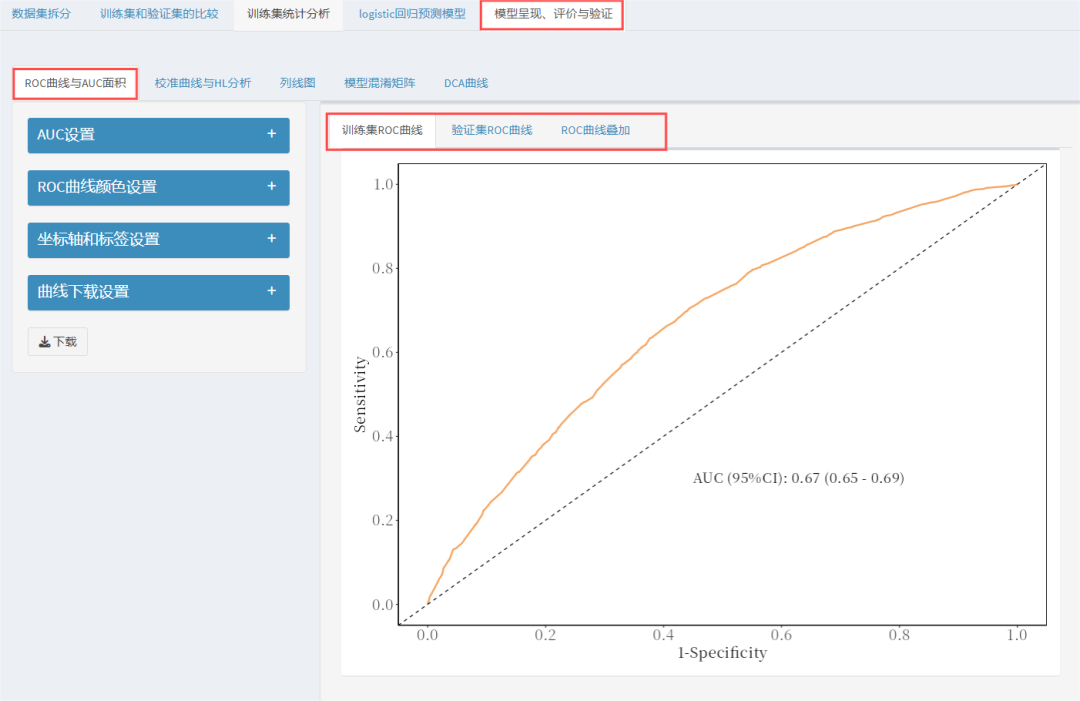
ROC曲线叠加:
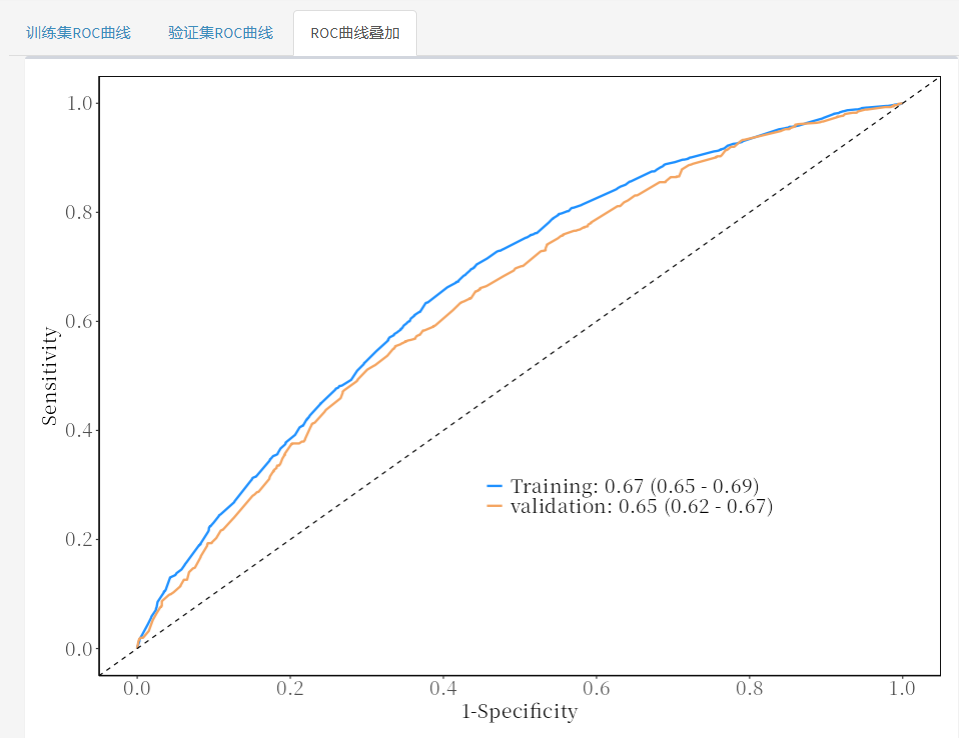
如果需要修改图例名称,可以在左侧的"AUC设置"这里进行修改,但是目前平台仅支持英文标签,如需添加中文,还需要下载pdf后,再进行二次编辑。
除此之外,平台还支持对ROC曲线的颜色、坐标轴、标签进行修改,将R语言繁杂的代码参数,全部简化为了菜单式操作!

5.下载结果
最后在曲线下载设置中,选择下载图片,保存类型(支持pdf、jpeg、png、tiff),曲线页面,中文字体。
注:如果图形下载下来不完全,可以在曲线页面设置自定义。自由调整图片的长度和宽度,避免下载图形不完整的情况。
选择完毕后,就可以下载ROC曲线啦!
下载下来的图片也十分清晰!
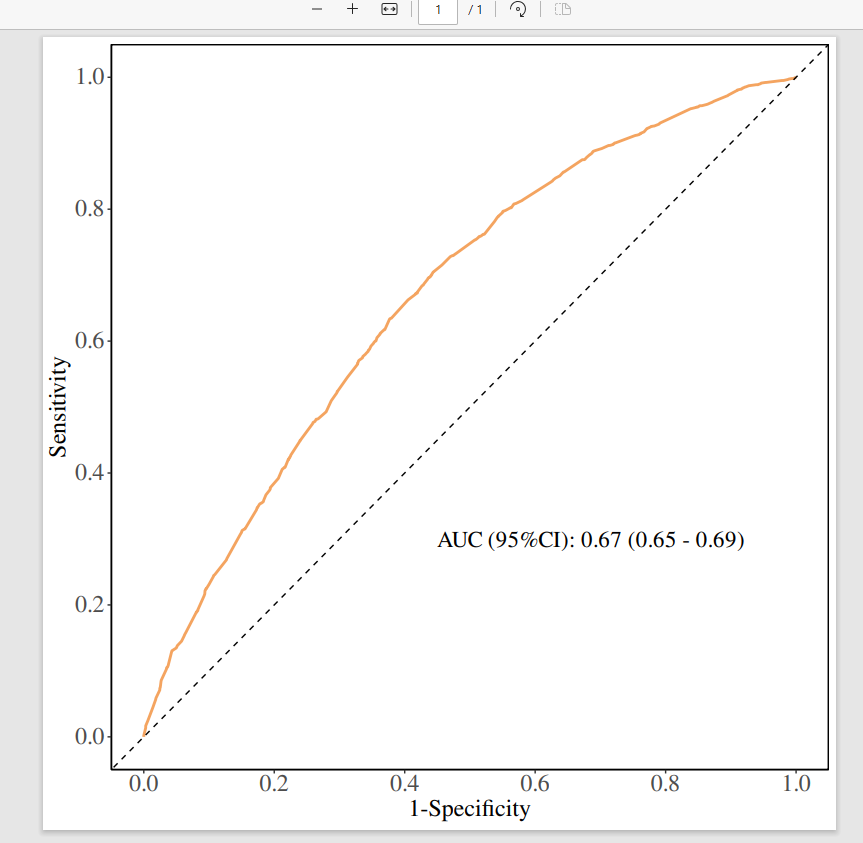
以上就是风暴统计平台绘制ROC曲线的全部操作流程啦!如果您在使用过程中出现报错,可以参考下方推文,排查一下问题所在哦!
答疑 | 风暴统计更换服务器后,为什么总出现同样的报错?