目录
1 算法题目................................... 3
1.1 盛最多水的容器.......................... 3
1.1.1 题目................................ 3
1.1.2 双指针.............................. 4
1.1.3 代码................................ 5
1.2 分巧克力................................ 5
1.2.1 题目................................ 5
1.2.2 二分答案............................ 6
1.2.3 代码................................ 6
1.3子序列的平均值.......................... 7
1.3.1 题目................................ 7
1.3.2 二分................................ 7
1.3.3 代码................................ 7
1.4伐木工人................................ 8
1.4.1 题目................................ 9
1.4.2 二分................................ 9
1.4.3 代码............................... 10
1.5 数列分段.............................. 11
1.5.1 题目............................... 11
1.5.2 二分答案........................... 12
1.5.3 代码............................... 12
1.6 进击的奶牛............................. 14
1.6.1 题目............................... 14
1.6.2 二分答案........................... 14
1.6.3 代码............................... 14
1.7 RPG难题............................... 16
1.7.1 题目............................... 16
1.7.2 dp................................. 16
1.7.3 代码............................... 17
1.8 Accidental Victory..................... 17
1.8.1 题目............................... 17
1.8.2前缀和............................. 17
1.8.3 代码............................... 18
1.9 mod M.................................. 19
1.9.1 题目............................... 19
1.9.2 gcd................................ 20
1.9.3 代码............................... 21
1.10 鸡数题................................ 21
1.10.1 题目.............................. 22
1.10.2 第二类斯特林数.................... 22
1.10.3 代码.............................. 22
1.11 Corn Fields G......................... 24
1.11.1 题目.............................. 24
1.11.2 dp................................ 24
1.11.3 代码.............................. 25
1.12 冒泡排序和最长子段和.................. 27
1.12.1 题目.............................. 27
1.12.2暴力.............................. 27
1.12.3 代码.............................. 27
2 获奖情况.................................. 28
3 感悟...................................... 29
4 参考文献.................................. 31
1.1 盛最多水的容器
1.1.1 题目
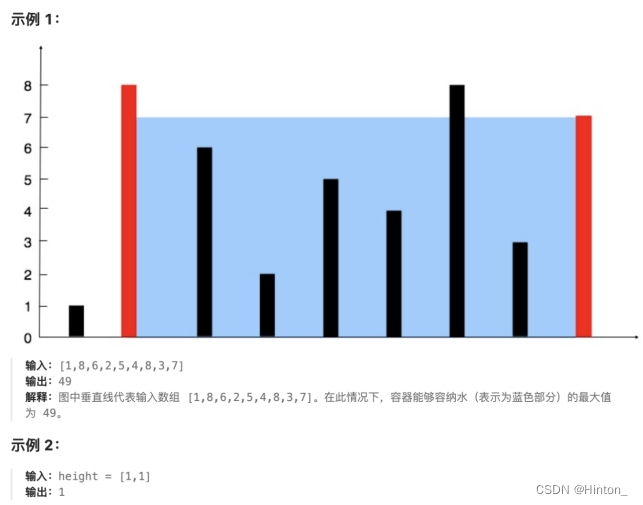
给定一个长度为 n 的整数数组 height
有 n 条垂线,第 i 条线的两个端点是 (i, 0) 和 (i, height[i])
找出其中的两条线,使得它们与 x 轴共同构成的容器可以容纳最多的水
返回容器可以储存的最大水量
说明:你不能倾斜容器。
1.1.2 双指针
在每个状态下,无论长板或短板向中间收窄一格,都会导致水槽 底边宽度变短,高度不定
向内移动短板 ,水槽的短板 min(h[i],h[j]) 可能变大,因此下个水槽的面积 可能增大。
向内移动长板 ,水槽的短板 min(h[i],h[j]) 不变或变小,因此下个水槽的面积 一定变小。
暴力枚举,水槽两板围成面积 S(i,j)的状态总数为 C(n,2)
假设状态 S(i,j)下 h[i]<h[j],在向内移动短板至 S(i+1,j),则相当于消去了 S(i,j1),S(i,j2),…,S(i,i+1)状态集合。
而所有消去状态的面积一定都小于当前面积,因为这些状态:
短板高度:相比 S(i,j)相同或更短
底边宽度:相比 S(i,j)更短;
因此,每轮向内移动短板,所有消去的状态都 不会导致面积最大值丢失
1.1.3 代码
int maxArea(vector<int> &height)
{
int i = 0, j = height.size() - 1, area, res = 0;
while (i < j)
{
area = (j - i) * fmin(height[i], height[j]);
res = max(area, res);
if (height[i] < height[j])
i++;
else
j--;
}
return res;
}1.2 分巧克力
1.2.1 题目
儿童节那天有 K位小朋友到小明家做客。小明拿出了珍藏的巧克力招待小朋友们。
小明一共有 N块巧克力,其中第 i块是 Hi×Wi的方格组成的长方形。
为了公平起见,小明需要从这 N 块巧克力中切出 K 块巧克力分给小朋友们。切出的巧克力需要满足:
形状是正方形,边长是整数。
大小相同。
例如一块 6×5 的巧克力可以切出 6 块 2×2 的巧克力或者 2块 3×3 的巧克力。
1.2.2 二分答案
读题 => 每块巧克力可以切得块数为 (H / mid) * (w / mid)
从d = 1开始一个一个试, 会超时采取二分, 在[1, 100000]开始试
1.2.3 代码
int Fun(int x)
{
int sum = 0;
for (int i = 1; i <= n; i++)
sum += (h[i] / x) * (w[i] / x);
if (sum >= k)
return 1;
return 0;
}
void solve()
{
int i;
cin >> n >> k;
for (i = 1; i <= n; i++)
cin >> h[i] >> w[i];
int left = 1, right = MAX, mid;
while (left < right)
{
mid = (left + right + 1) / 2;
if (Fun(mid))
left = mid;
else
right = mid - 1;
}
cout << left;
}1.3子序列的平均值
1.3.1 题目
给定一个长度为n的非负序列A,请你找出一个长度不小于L的子段(子段是序列A中一些连续的元素构成的集合),使得子段中数值的平均值最大。最终输出这个最大的平均值。
输入格式:
第一行两个整数n, L(1<=L<=n<=100000)
以下n行,每行一个非负整数,表示序列A中每个元素的值。
1.3.2 二分
答案一定位于最小值和最大值之间
check的标准: 序列和 / L 如果大于mid,说明平均值可以更大l = mid;
如果小于mid,说明平均值不够这么大r = mid;
1.3.3 代码
#include <iostream>
#include <cmath>
using namespace std;
int n = 0, L = 0;
double a[100001] = {0};
bool Check(double average)
{
bool flag = false;
double sum[100001] = {0};
for (int i = 1; i <= n; ++i)
{
sum[i] = sum[i - 1] + (a[i] - average);
}
double fronts = 1e9;
for (int i = L; i <= n; ++i)
{
fronts = fmin(fronts, sum[i - L]);
if (sum[i] - fronts > 0)
{
flag = true;
break;
}
}
return flag;
}
int main()
{
cin >> n >> L;
double max = 0, min = 1e9;
for (int i = 1; i <= n; ++i)
{
cin >> a[i];
max = fmax(a[i], max);
min = fmin(a[i], min);
}
double low = min, high = max, answer = (low + high) / 2;
while (high - low > 1e-5)
{
if (Check(answer))
low = answer;
else
high = answer;
answer = (low + high) / 2;
}
cout << (int)(high * 1000) << endl;
}1.4伐木工人
1.4.1 题目
伐木工人 Mirko 需要砍 M 米长的木材。对 Mirko 来说这是很简单的工作,因为他有一个漂亮的新伐木机,可以如野火一般砍伐森林。不过,Mirko 只被允许砍伐一排树。
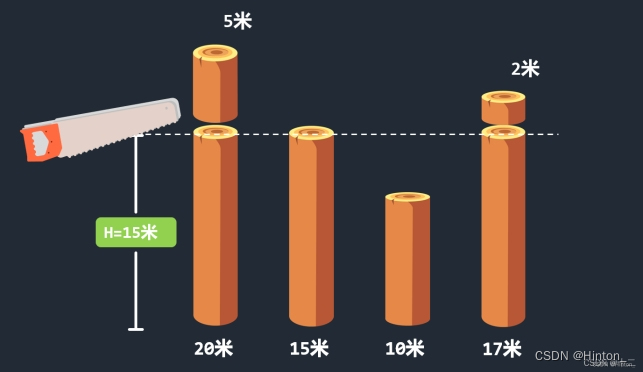
Mirko的伐木机工作流程如下:Mirko 设置一个高度参数 H(米),伐木机升起一个巨大的锯片到高度 H,并锯掉所有树比 H 高的部分(当然,树木不高于 H 米的部分保持不变)。Mirko 就得到树木被锯下的部分。例如,如果一排树的高度分别为 20,15,10 和17,Mirko 把锯片升到 15 米的高度,切割后树木剩下的高度将是 15,15,10 和 15,而 Mirko 将从第 1 棵树得到 5米,从第 4 棵树得到 2 米,共得到 7 米木材。
Mirko 非常关注生态保护,所以他不会砍掉过多的木材。这也是他尽可能高地设定伐木机锯片的原因。请帮助 Mirko 找到伐木机锯片的最大的整数高度 H,使得他能得到的木材至少为 M 米。换句话说,如果再升高 1 米,他将得不到 M 米木材。
输入
第 1 行 2 个整数 N 和 M,N 表示树木的数量,M 表示需要的木材总长度。
第 2 行 N 个整数表示每棵树的高度。
输出1 个整数,表示锯片的最高高度
1.4.2 二分
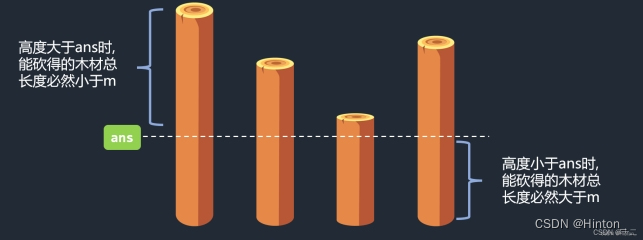
大于 ans 的高度,不满足条件,小于 ans 的高度,都满足条件.
①要求满足条件的最大高度,那么首先答案介于0-树的最大高度Heigt.
②用二分查找的框架去判断 mid符合条件,然后根据判断结果去更新答案区间
得到的总长度sum ≥ m说明高度低了->left变为mid + 1;
否则 right 变为 mid - 1;
1.4.3 代码
#include <bits/stdc++.h>
using namespace std;
int n, m, a[1000005], height;
int Binary_answer(int h)
{
int left = 0, right = h, mid, ans;
while (left <= right)
{
mid = (left + right) / 2;
long long sum = 0;
for (int i = 1; i <= n; i++)
{
if (a[i] > mid)
sum += a[i] - mid;
}
if (sum >= m)
ans = mid, left = mid + 1;
else
right = mid - 1;
}
return ans;
}
int main()
{
cin >> n >> m;
for (int i = 1; i <= n; i++)
{
cin >> a[i];
if (a[i] > height)
height = a[i];
}
cout << Binary_answer(height);
return 0;
}1.5 数列分段
1.5.1 题目
对于给定的一个长度为N的正整数数列 A 1 ∼ N A _{1∼N}A1∼N.
现要将其分成 M(M≤N)段,并要求每段连续,且每段和的最大值最小。
关于最大值最小:
例如一数列 4 2 4 5 1 要分成 3 段。
将其如下分段: [4 2][4 5][1]
第一段和为 6,第 2 段和为 9,第 3 段和为 1,和最大值为 9。
将其如下分段: [4][2 4][5 1]
第一段和为 4,第 2 段和为 6,第 3 段和为 6,和最大值为 6。
并且无论如何分段,最大值不会小于 6。
所以可以得到要将数列 4 2 4 5 1 要分成 3 段,每段和的最大值最小为 6。
1.5.2 二分答案
确定最大值所在的区间,left 和 right
二分判断最大值为 mid 时数列是否可以分成 m 段
根据判断结果更新区间
得到符合题目要求的答案
完成第一步,确定区间。要求最大值最小,则该值必定是大于数列中的最大值的(最大值单独为一段的时候),最大值则为所有数列之和。所以最大值的区间 left=数列中的最大值,right=数列的所有数相加之和,则:
1.5.3 代码
int n, m, a[100005];
cin >> n >> m;
for (i = 1; i <= n; i++)
{
cin >> a[i];
sum += a[i]; // sum为答案右边界
mx = max(mx, a[i]); // mx为答案左边界
}二分判断最大值为 mid 时,数列是否可以分成 m 段,采用贪心策略,分割的每一段的总和尽量接近但不超过 mid,则:
while (left <= right)
{
mid = (left + right) / 2;
// 计算最大值为mid时,能分割的段数
int sum1 = 0, cnt = 1; // 分别表示当前这一段的数字总和、数列目前段数
for (int i = 1; i <= n; i++)
{
// 判断a[i]是否可以连接到当前这段数字中
if (sum1 + a[i] <= mid)
sum1 += a[i]; // sum+a[i]不超过mid则可以继续连接
else
sum1 = a[i], cnt++; // 否则a[i]自起一段,数列总段数cnt+1
}
}根据判断结果更新区间,因为是求最大值的最小,所以区间上是向左找的。
当 cnt<=m 时,说明 mid 值偏大,此时去查看更小的,即 ans=mid,right=mid-1,如果分割的段数超过 m 段,说明 mid 要更大一点,即 left=mid+1。
// 判断结果,更新区间
if (cnt <= m)
ans = mid, right = mid - 1;
else
left = mid + 1;
#include <bits / stdc++.h>
using namespace std;
int n, m, a[100005];
int sum, mx;
int Binary_answer(int l, int r)
{
int left = l, right = r, mid, ans;
while (left <= right)
{
mid = (left + right) / 2;
// 计算最大值为mid时,能分割的段数
int sum1 = 0, cnt = 1; // 分别表示当前这一段的数字总和、数列目前段数
for (int i = 1; i <= n; i++)
{
// 判断a[i]是否可以连接到当前这段数字中
if (sum1 + a[i] <= mid)
sum1 += a[i]; // sum+a[i]不超过mid则可以继续连接
else
sum1 = a[i], cnt++; // 否则a[i]自起一段,数列总段数cnt+1
}
// 判断结果,更新区间
if (cnt <= m)
ans = mid, right = mid - 1;
else
left = mid + 1;
}
return ans;
}
int main()
{
cin >> n >> m;
for (int i = 1; i <= n; i++)
{
cin >> a[i];
sum += a[i]; // sum为答案右边界
mx = max(mx, a[i]); // mx为答案左边界
}
// 二分答案
cout << Binary_answer(mx, sum);
return 0;
}1.6 进击的奶牛
1.6.1 题目
Farmer John 建造了一个有 N(2≤ N ≤100000)个隔间的牛棚,这些隔间分布在一条直线上,坐标是 x1…xN他的 C(2≤ C≤ N)头牛不满于隔间的位置分布,它们为牛棚里其他的牛的存在而愤怒。为了防止牛之间的互相打斗,Farmer John 想把这些牛安置在指定的隔间,所有牛中相邻两头的最近距离越大越好。那么,这个最大的最近距离是多少呢?
1.6.2 二分答案
确定最大值所在的区间,left 和 right
二分判断最小值为 mid 时数列是否可以安置 m 头奶牛
根据判断结果更新区间
得到符合题目要求的答案
1.6.3 代码
#include <bits/stdc++.h>
using namespace std;
int n, m, a[100005];
int mn, mx;
int Binary_answer(int l, int r)
{
int left = l, right = r, mid, ans;
while (left <= right)
{
mid = (left + right) / 2;
// 计算最小值为mid时可以放置的奶牛数量
int index = 1, cnt = 1; // index为当前坐标,cnt为奶牛数量
for (int i = 2; i <= n; i++)
{
// 判断a[i]和当前坐标之前的差值
if (a[i] - a[index] >= mid)
index = i, cnt++; // 条件成立,更新坐标,奶牛数量+1
}
// 判断结果,更新区间
if (cnt >= m)
ans = mid, left = mid + 1;
else
right = mid - 1;
}
return ans;
}
int main()
{
cin >> n >> m;
for (int i = 1; i <= n; i++)
{
cin >> a[i];
}
// 将坐标从小到大排序,方便计算
sort(a + 1, a + n + 1);
// 确定区间最大值和最小值
mn = 1; // 默认最小值为1,就是紧挨着
mx = a[n] - a[1]; // 最大值为最后一个坐标减第一个坐标
// 二分答案
cout << Binary_answer(mn, mx);
return 0;
}1.7 RPG难题
1.7.1 题目
有排成一行的n个方格,用红(Red)、粉(Pink)、绿(Green)三色涂每个格子,每格涂一色,要求任何相邻的方格不能同色,且首尾两格也不同色.求全部的满足要求的涂法.
以上就是著名的RPG难题.
输入数据包含多个测试实例,每个测试实例占一行,由一个整数N组成,(0 < n <= 50)。
对于每个测试实例,请输出全部的满足要求的涂法,每个实例的输出占一行。
1.7.2 dp
易知dp(1)=3; dp(2)=6; dp(3)=6; dp(4)=18;
考虑n>3的情况
第n-1个格子和第一个格子不同,则为dp(n-1)
第n-1个格子和第1个格子相同,则第n-2个格子和第一个格子必然不同,此时为dp(n-2)再乘第n-1个格子的颜色数,很显然第n-1个格子可以是第一个格子(即第n-2个格子)的颜色外的另外两种,这样为2 * dp(n-2);
因此总的情况为dp(n)=dp(n-1)+2*dp(n-2)
2个限制条件
相邻的方格不能同色
首尾两格不同色
n = 1时, 解为R, P, G
n = 2时, 可以在n = 1字符串后面加一个字符得到
在R后面可以加P和G, 但是不能加R, 如RP, RG
同理,可得 n = 2时一共有6组解
n = 3时, 由于n = 2时的字符串已经包含2个不同的字符,所以只有一种选择,还是6组解
n = 4时, 可以直接在n = 3的字符串后面加一个字符,也只有一个字符可以选择.
但是, 如果n = 3字符串违背条件2, 那原本错误的答案,加上一个字符后就会变成一个正确的答案
所以, 后面加的这个字符和头部字符不相同,那就和他前面相邻的字符不同,但是这两个字符是相同的, 因此a[4] = a[3] + 2 * a[2]
得出关系式
dp[i] = dp[i - 1] + 2 * dp[i - 2];
1.7.3 代码
#include <bits/stdc++.h>
using namespace std;
int a[10005], dp[10005];
int main()
{
int n;
while (scanf("%d", &n) != EOF)
{
a[1] = 3;
a[2] = 6;
a[3] = 6;
for (i = 4; i <= n; i++)
{
a[i] = a[i - 1] + 2 * a[i - 2];
}
cout << a[n] << endl;
}
return 0;
}- 1.8 Accidental Victory
1.8.1 题目
有 n支队伍参加比赛,每个队伍初始时有一些代币。
比赛每一轮随机挑两个代币数不为0的队伍,然后代币多的队伍获胜,代币少的队伍把代币全部给代币多的(代币数量相同则随机),直到最后只有一个队伍有代币, 这个队伍获胜。
求哪些队伍是有可能获胜的。
1.8.2前缀和
先排序, 判断是否可以打败第一个之前比他强的选手
如果行, 打败
这个选手打败第一个比他强的选手最终的实力和这一个后者选手打败所有比他弱的最终的实力一样, 如果能这样持续到最后一个 那么这一个肯定行
一个人想赢, 需要打败比他弱的选手
寻找最后一个不可以完成的下标即可。
1.8.3 代码
#include <bits/stdc++.h>
typedef long long ll;
using namespace std;
const int maxn = 2e5 + 50;
typedef struct node
{
ll Num;
index;
} player;
player a[maxn];
bool cmp(player m, player n)
{
return m.Num < n.Num;
}
void solve()
{
set<int> ans; // set自动排序 题目要求最终"increasing order"
ans.clear();
int n, i;
cin >> n;
for (i = 1; i <= n; i++)
{
scanf("%lld", &a[i].Num);
a[i].index = i;
}
sort(a + 1, a + 1 + n, cmp);
for (i = 2; i <= n; i++)
a[i].Num += a[i - 1].Num;
int Last = 0;
for (i = n - 1; i >= 0; i--)
{
if (a[i].Num < a[i + 1].Num - a[i].Num)
{
Last = i + 1;
break;
}
}
for (i = Last; i <= n; i++)
ans.insert(a[i].index);
cout << ans.size() << endl;
for (set<int>::iterator it = ans.begin(); it != ans.end(); it++)
cout << *it << ' ';
cout << endl;
}
int main()
{
int T;
cin >> T;
while (T--)
solve();
return 0;
}-
-
1.9 mod M
-
1.9.1 题目
给出一个有 n nn 个非负整数的数列 A AA
现在进行以下的一次操作:
将 A 中所有数对一个大于等于2的整数 M 取模,替换掉原来的数
例如A=(2,7,4) ,取 M=4 ,则操作后 A=(2mod4, 7mod4, 4mod4) = (2, 3, 0)
请问,操作后的数列 A 最少能有多少种不同的数字。
1.9.2 gcd
当m=2时,ai的取值只可能为0或1,因此,答案最多为2。
接下来我们考虑答案为1的情况。
显然,当gcd{a1 - a2, a2 - a3,an-1 - an}不为1时,即相邻两数的差值的最小公约数不为1时,
我们就可以去它们的最小公约数,这样可以保证同为1个数。
// 这个会编译错误
#include <bits/stdc++.h>
using namespace std;
const int maxn = 2e5 + 5;
int a[maxn] = {0};
int gcd(int a, int b)
{
if (b == 0)
return a;
return gcd(b, a % b);
}
int main()
{
int n, i;
cin >> n;
for (i = 1; i <= n; i++)
cin >> a[i];
int g = 0;
for (i = 2; i <= n; i++)
{
g = gcd(g, fabs(a[i] - a[i - 1]));
}
if (g == 1)
puts("2");
else
puts("1");
}得到缘由
fabs 返回double类型,而传入的参数为int类型
abs 返回 int 类型
1.9.3 代码
#include <bits/stdc++.h>
using namespace std;
const int maxn = 2e5 + 5;
int a[maxn] = {0};
int gcd(int a, int b)
{
if (b == 0)
return a;
return gcd(b, a % b);
}
int main()
{
int n, i;
cin >> n;
for (i = 1; i <= n; i++)
cin >> a[i];
int g = 0;
for (i = 2; i <= n; i++)
{
g = gcd(g, (int)fabs(a[i] - a[i - 1]));
}
if (g == 1)
puts("2");
else
puts("1");
}1.10 鸡数题
1.10.1 题目
n个不同的小球放在m个相同的箱子里,求方案数
1.10.2 第二类斯特林数
把n个不同的数划分为m个集合的方案数(S(n, m), 与第一类不同, 划分集合不需要考虑排列次序)
递推关系
S(n - 1, m - 1) 将n - 1个不同元素划分为m - 1个集合, 则第n个元素必须单独放入第m个集合
S(n - 1, m) * m 将 n - 1个不同元素已经划分为m个集合, 则第n个元素可以放在m个集合中任意一个里面
得关系式 S(n, m) = S(n - 1, m - 1) + S(n - 1, m) * m
S(0,0) = 1
S ( n , 0 ) S(n, 0)S(n,0) = 0
S ( n , 1 ) S(n, 1)S(n,1) = 1
S ( n , n ) S(n, n)S(n,n) = 1
S ( n , 2 ) S(n, 2)S(n,2) = 2 ^(n - 1) - 1
S ( n , n − 1 ) S(n, n - 1)S(n,n−1) = n * (n - 1) / 2
m个数按位或结果是2 ^ n - 1 ==> 右边前n位都至少有一个数该为为1
任意两个数按位与等于0 ==> 任意两个数都没有任意一位相同, 右侧前n位每一位有且只有一个数该位为1
m个数升序 ==> 只能升序排列
m个数都不为0 ==> 每个数都至少有一个数位为1
1.10.3 代码
#include <bits/stdc++.h>
using namespace std;
const int P = 1000000007;
long long *fac, *ifac;
long long power(long long a, long long b, int p = P)
{
long long res = 1;
for (; b; b >>= 1, a = a * a % p)
if (b & 1)
res = res * a % p;
return res;
}
long long inv(long long x)
{
return power(x, P - 2);
}
void init(int N)
{
int i;
fac = new long long[N + 1];
ifac = new long long[N + 1];
fac[0] = 1;
for (i = 1; i <= N; i++)
fac[i] = fac[i - 1] * i % P;
ifac[N] = inv(fac[N]);
for (i = N - 1; i >= 0; i--)
ifac[i] = ifac[i + 1] * (i + 1) % P;
}
long long C(int n, int m)
{
if (m < 0 || m > n || n < 0)
{
return 0;
}
return fac[n] * ifac[m] % P * ifac[n - m] % P;
}
int main()
{
int n, m, k;
cin >> n >> m;
init(m);
long long ans = 0;
for (k = 0; k <= m; k++)
{
if (k % 2 == 0)
ans = (ans + C(m, k) * power(m - k, n) % P) % P;
else
ans = (ans - C(m, k) * power(m - k, n) % P + P) % P;
}
cout << ans * ifac[m] % P << '\n';
}1.11 Corn Fields G
1.11.1 题目
农场主 JohnJohn 新买了一块长方形的新牧场,这块牧场被划分成𝑀行𝑁列(1≤M≤12,1≤N≤12),每一格都是一块正方形的土地。 John打算在牧场上的某几格里种上美味的草,供他的奶牛们享用。
遗憾的是,有些土地相当贫瘠,不能用来种草。并且,奶牛们喜欢独占一块草地的感觉,于是John不会选择两块相邻的土地,也就是说,没有哪两块草地有公共边。
John想知道,如果不考虑草地的总块数,那么,一共有多少种种植方案可供他选择?(当然,把新牧场完全荒废也是一种方案)
1.11.2 dp
对于每一行,我们就可以看成一个未知集合,而集合的大小自然就是列m
对于每一个单元,其取值范围为0, 1 ,而1 代表放置奶牛,0 代表不放置奶牛
用二进制表示,那么状态总数就是( 1 << m ) − 1
对于每一个状态,我们需要判断是否合格,而其中明确不能选择两块相邻的土地,在集合内,即相邻位不能全为1 ,所以我们可以预处理g 数组,处理方式即为:g[i] = !(i & (i << 1));
同样,我们还应该知晓土地的状况,因为毕竟只有土地肥沃才可以放置奶牛,则我们可以通过一个st数组判断,集合与集合之间,我们也需要考虑相邻位不能全为1,所以在枚举上一个集合的状态也需要严格判断。对于状态定义,我们可以用f[i][j]表示第i 行且状态为j jj的方案数。对于状态转移,假设上一行状态为k kk,则状态转移方程为:
f[i][j] += f[i - 1][k];
1.11.3 代码
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N = 10 + 5, M = 10 + 5;
const int P = 1e8;
int n, m, i, j; // n行m列的土地。
int a[N][M], st[N]; // a代表土地,st代表每一行的土地状况。
bool g[1 << N]; // g得到所有状态中的合法状态。
int f[N][1 << N]; // f[i][j]表示的则是第i行且状态为j的方案数,是由上一行转移过来的,所以我们定义上一行的状态为k。
// 则状态转移方程为f[i][j] += f[i - 1][k];//其中j和k必须满足条件。
int main()
{
cin >> n >> m;
for (i = 1; i <= n; i++)
{
for (j = 1; j <= m; j++)
{
scanf("%d", &a[i][j]);
}
}
// 得到每一行的土地状况。
for (i = 1; i <= n; i++)
{
for (int j = 1; j <= m; j++)
{
st[i] = (st[i] << 1) + a[i][j];
}
}
// 得到所有状态中的合法状态。
int maxn = 1 << m; // 总状态。
f[0][0] = 1; // 初始化,这种也算一种。
for (i = 0; i < maxn; i++)
{
g[i] = !(i & (i << 1)); // 由于不能相邻,所以我们左移判断是否符合条件。
}
for (i = 1; i <= n; i++)
{
// 枚举每一行。
for (int j = 0; j < maxn; j++)
{
// 枚举每一行的状态,判断此状态是否符合条件。1.不能相邻。2.是全部状态的子集。
if (g[j] && (j & st[i]) == j)
{
// 如果符合条件。则我们去判断上一行是否符合。
for (int k = 0; k < maxn; ++k)
{
// 枚举上一行状态。注意,这里我们无需判断上一行状态是否存在,因为不存在即为0.
// 只需要判断j和k是否存在相邻草地。
if (!(j & k))
{
f[i][j] = (f[i][j] + f[i - 1][k]) % P;
}
}
}
}
}
int ans = 0;
for (int j = 0; j < maxn; j++)
{
ans = (ans + f[n][j]) % P;
}
cout << ans << endl;
}1.12 冒泡排序和最长子段和
1.12.1 题目
给定一个长度为n nn的数组, 求恰好执行“交换任意相邻元素”操作k次后,数组的最大非空子段和。
1.12.2暴力
k∈[0,1] 暴力枚举
最大非空子段和 ==> 贪心
c u r curcur为 包含当前位置元素的最大子段和
从a[2]开始遍历数组, 则当前最大子段和有2种情况
将当前位置的元素加入到最大子段和, cur + a[i]
当前位置的元素为起点, 重新开始计算最大字段和, 值为a[i], cur取这2种情况的较大值, 每个位置cur的最大值即为最大非空子段和k∈ [0, 1]
最大非空子段和 ==> 贪心
rcur为 包含当前位置元素的最大子段和
从a[2] 开始遍历数组, 则当前最大子段和有2种情况
将当前位置的元素加入到最大子段和, cur + a[i] 当前位置的元素为起点, 重新开始计算最大字段和, 值为a[i]
cur取这2种情况的较大值, 每个位置cur的最大值即为最大非空子段和
1.12.3 代码
void solve()
{
int i, j, n, k;
cin >> n >> k;
for (i = 1; i <= n; i++)
cin >> a[i];
for (i = 1; i <= n - 1; i++)
{
if (k == 1)
swap(a[i], a[i + 1]);
for (j = 1; j <= n; j++)
{
sum[j] = max(sum[j - 1] + a[j], a[j]);
ans = max(ans, sum[j]);
}
if (k == 1)
swap(a[i], a[i + 1]);
}
cout << ans << endl;
}- 参考文献
CSDN: Hinton_-CSDN博客
OIWiKi: OI Wiki - OI Wiki
Labulangdong: 双指针技巧秒杀七道链表题目 | labuladong 的算法笔记
牛客题单:【题解】2024牛客寒假算法基础集训营6_ICPC/CCPC/NOIP/NOI刷题训练题单_牛客竞赛OJ