摘要
本研究提出了一种基于遗传算法的车辆路径规划(VRP)问题求解框架,它能够有效地处理一系列复杂约束,包括软时间窗、硬时间窗、行驶距离限制、车辆最大载重量、多个配送中心的协调、特定的配送顺序,以及多种车型的选择。该框架的一个关键特点在于其与其他算法的结合潜力,特别是可以快速与模拟退火、领域搜索等算法快速结合,以便开发出混合优化算法,这一能力将进一步加强搜索效率和解的质量。本文主要介绍算法框架的编码、解码以及交叉变异等内容,并以一个简单实例论证框架的可行性。
VRP问题
问题定义
车辆路径问题(VRP)涉及服务一组客户,每个客户都有某些货物的需求。目标是为一组车辆规划路线,使所有客户都得到服务。核心问题是确定哪辆车应服务哪些客户,以及访问顺序,以最小化总路线成本,这通常是指路线的总长度、总时间或使用的车辆数量。在VRP的最基本形式中,每辆车从配送中心出发,服务一系列客户,然后返回配送中心。每个客户被且只被一辆车服务一次。
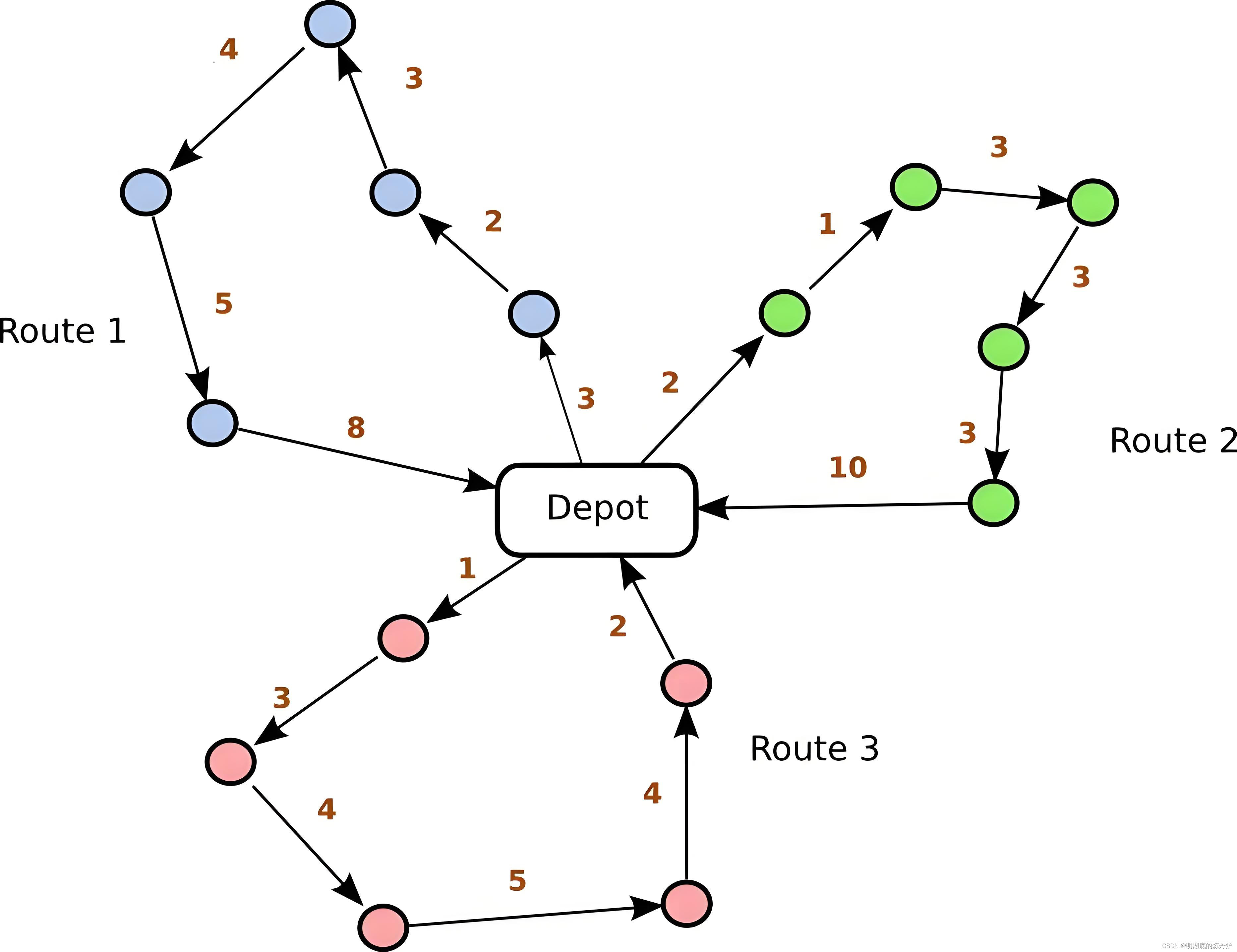
常见约束
(1)容量约束: 每辆车有最大的承载能力,不能超载服务客户。
(2)服务约束: 每辆车分配的路线必须在其工作时长内完成。
(3)时间窗约束: 对于VRP的变体VRPTW,每个客户可能会有一个服务 时间窗口,即服务必须在特定的时间内开始。
(4)车辆数目约束: 可用的车辆数量可能是有限的。
(5)客户需求约束: 每个客户的需求必须得到完全满足。
(6)行驶距离约束:每辆车有最大行驶距离。
(7)配送顺序约束:需求点之间存在配送先后顺序。
常用算法
(1)精确算法: 如线性规划、混合整数规划(使用专门的优化软件如CPLEX、Gurobi)、分支限界等算法,能够求解问题的最优解,但随着问题规模的增加,计算复杂度会迅速上升。
(2)启发式算法: 如节约算法、插入算法、Sweep算法等,它们可以在有限时间内为VRP问题找到较好的解,但不保证最优。
(3)元启发式算法: 如模拟退火、遗传算法、禁忌搜索、蚁群算法、粒子群优化等,这些算法通过迭代搜索来改进解,通常能够产生高质量的近似最优解,适用于大规模问题。
(4)混合启发式: 结合两种或多种启发式或元启发式算法,利用它们各自的优点,以获得更优解。例如,先使用一个启发式算法生成初始解,然后应用另一个不同类型的启发式算法来进一步改进解。
算法设计
遗传算法(Genetic Algorithms, GA)是一种借鉴生物进化过程的全局优化搜索算法,通过自然选择和遗传机制(如交叉、变异)来逐代演化出问题的解。在求解车辆路径问题(Vehicle Routing Problem, VRP)时,遗传算法通过模拟自然选择和遗传机制,提供了一个弹性、高效和鲁棒的途径,适用于各种复杂的变体和实际应用场景。
算子编码
为了支持前文提到的所有约束,本文算子编码采用三段式编码,第一段为需求点遍历顺序的编码,第二段为车辆覆盖范围的编码,第三段为配送点选择的编码。假设对于一个需求点数量为8,车辆数为3,配送中心数量为2的VRP问题,某个个体编码如下。
[0,1,2,3,4,5,6,7,3,5,8,9,8]
该段编码中[0,1,2,3,4,5,6,7]为需求点遍历顺序编码。[3,5]为车辆覆盖范围编码,即第1辆车覆盖范围为[0,3),第二辆车覆盖范围为[3,5),第三辆车的覆盖范围为[5,8)。[0,1,0]为配送中心编码,表示三辆车分配来自配送点8、9、8。因此,改个体的配送路径为:
[8,0,1,2,8]
[9,3,4,9]
[8,5,6,7,8]
下面是生成种群个体的代码:
'''
生成单个个体
'''
def gen_individual(self):
# 需求点遍历顺序
individual=[i for i in range(self.vrp.costomer_num)]
random.shuffle(individual)
# 车辆分割点
cur=0
for i in range(self.car_num-1):
rnd=randint(cur+1,self.vrp.costomer_num-self.car_num+i+1)
cur=rnd
individual.append(cur)
# 仓库选择
for i in range(self.car_num):
individual.append(randint(self.vrp.costomer_num,costomer_num+self.vrp.warehouse_num-1))
return self.adjust_individual(individual)
算子交叉
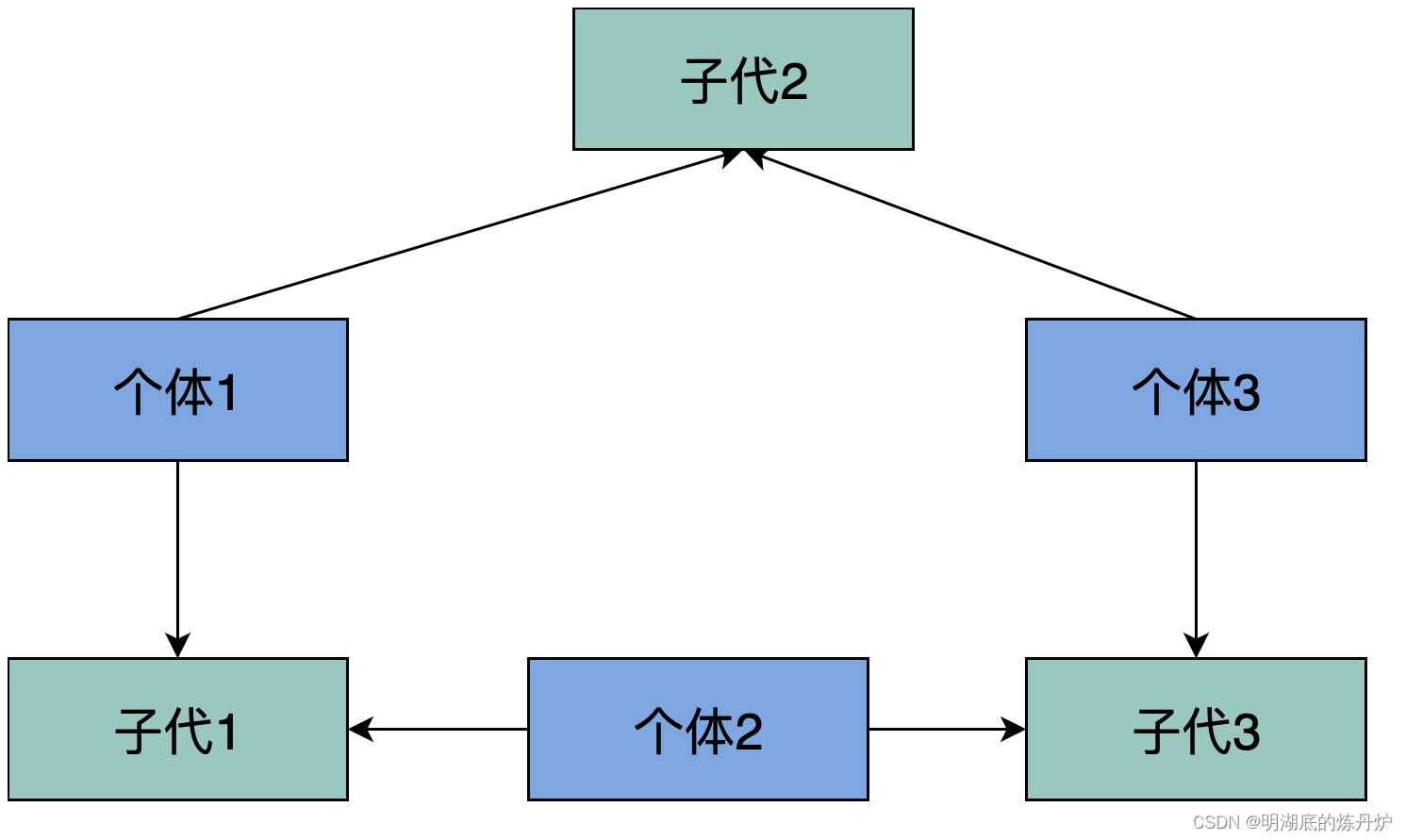
交叉是遗传算法中最重要的操作之一,本文交叉操作采用三个个体两两交叉的方式,三个个体两两交叉,产生的个体数仍然为三,能够有效维持种群稳定性
'''
三个个体交叉
'''
def triple_cross_individual(self,individual1,individual2,individual3):
child1=self.double_cross_individual(individual1,individual2)
child2=self.double_cross_individual(individual1,individual3)
child3=self.double_cross_individual(individual2,individual3)
return (child1,child2,child3)
交叉方式分为四步,第一步是需求点遍历顺序的交叉,需求点遍历顺序的交叉为均匀交叉,假设个体1的需求点遍历顺序为[0,1,2,3],个体2需求点的便利顺序为[3,2,1,0],即每次生成一个随机数,根据随机数的取值将个体1和个体2的当前需求点分配给子代1和子代2。第二步是车辆覆盖范围的交叉,采用单次交叉的交叉方式,生成一次随机数,根据随机数的取值将个体1个个体2的编码整段分配给子代1和子代2。第三步是配送中心编码的交叉,配送中心编码的交叉与第一步一直,多次生成随机数,而后将子代1和2的对应编码值按照随机数赋给子代1和子代2。第四步是择优,即选择适应度更优的个体作为最终被接受的子代。
'''
两个个体交叉
'''
def double_cross_individual(self,individual1,individual2):
child1,child2=[],[]
# 需求点遍历
for i in range(self.vrp.costomer_num):
rnd=randint(0,1)
if rnd:
if not individual1[i] in child1:
child1.append(individual1[i])
else:
child2.append(individual1[i])
if not individual2[i] in child1:
child1.append(individual2[i])
else:
child2.append(individual2[i])
else:
if not individual1[i] in child2:
child2.append(individual1[i])
else:
child1.append(individual1[i])
if not individual2[i] in child2:
child2.append(individual2[i])
else:
child1.append(individual2[i])
# 车辆切割点
rnd=randint(0,1)
if rnd:
child1+=individual1[self.vrp.costomer_num:self.vrp.costomer_num+self.car_num-1]
child2+=individual2[self.vrp.costomer_num:self.vrp.costomer_num+self.car_num-1]
else:
child1+=individual2[self.vrp.costomer_num:self.vrp.costomer_num+self.car_num-1]
child2+=individual1[self.vrp.costomer_num:self.vrp.costomer_num+self.car_num-1]
# 仓库选择
for i in range(self.car_num):
ii=self.vrp.costomer_num+self.car_num-1+i
rnd=randint(0,1)
if rnd:
child1.append(individual1[ii])
child2.append(individual2[ii])
else:
child1.append(individual2[ii])
child2.append(individual1[ii])
# 选择更好的child
child1=self.adjust_individual(child1)
child2=self.adjust_individual(child2)
if self.fitness_value(child1)>self.fitness_value(child2):
return child1
return child2
算子变异
算子变异是遗传算法的基础操作之一,其目的在于避免种群过早收敛,赋予一定跳出局部最优的能力。本文的算子变异包含两部分,一部分为需求点遍历顺序的变异,即随机选择两个需求点,对其进行位置互换。第二部分为配送中心变异,即随机选择一个配送中心,使其发生变化,转变为从另外一个仓库进行配送。
'''
个体变异
'''
def variate_individual(self,individual):
copy_individual=deepcopy(individual)
# 需求点遍历顺序变异
rnd=randint(0,1)
if rnd:
p=random.sample(copy_individual[:self.vrp.costomer_num],2)
temp=copy_individual[p[0]]
copy_individual[p[0]]=copy_individual[p[1]]
copy_individual[p[1]]=temp
# 仓库选择变异
rnd=randint(0,1)
if rnd:
idx=randint(0,self.car_num-1)
copy_individual[self.vrp.costomer_num+self.car_num-1+idx]=\
randint(self.vrp.costomer_num,costomer_num+self.vrp.warehouse_num-1)
return self.adjust_individual(copy_individual)
适应度函数
适应度是评价个体好坏的标准,本文考虑配送配送距离和时间窗的违背成本,通过加权方式将其结合起来。
'''
计算适应度
'''
def fitness_value(self,individual):
# 非可行解
if not individual:
return 0
# 路径解析
routes=self.resolve_individual(individual)
# 判断是否可行
if not self.valid_routes(routes):
return 0
# 总成本
total_cost=0
# 距离成本
for k in routes:
route=routes[k]
driving_distance=self.get_driving_distance(route)
total_cost+=driving_distance
# 时间成本
time_tables=self.get_time_table(routes)
for k in time_tables:
time_table=time_tables[k]
time_cost=self.get_time_cost(time_table)
total_cost+=time_cost
return 1/total_cost
实例分析
问题描述
本文以一个单配送中心的VRPTW问题为例,验证本文算法框架的有效性 。该问题描述为共有8个需求点,客户i的需求量为q_i,卸货时间为T_i,客户i要求车辆的到达时间为[ET_i,LT_i],各客户要求的具体数据如下表所示。

客户与需求点之间的距离如下表所示,在这里0表示配送中心,客户需要的所有需求,均由载重为10吨的车辆来完成,车辆速度为50km每小时,早到和晚到的成本都是50km,即每早到或晚到1h,等同于多走50km的距离。

结果展示
每代个体30个,迭代代数为100代,迭代结果如下图所示。

最终结果如下,配送车辆为3,配送距离为1055。
{0: [0, 8, 6, 4, 0], 1: [0, 3, 7, 2, 0], 2: [0, 1, 5, 0]}
本文总结
本研究展示了一种进阶的车辆路径规划(VRP)问题求解框架,重点在于遗传算法的核心应用和扩展性。文中详细阐述了算法的关键组成部分,包括个体编码、解码策略以及交叉和变异机制的设计,确保了可操作性和解的有效性。此外,文章通过一具体实例,证明了该框架不仅在理论上的可行性,同时其实践应用也显示出强大的问题解决能力。最终,本研究为解决复杂的VRP问题提供了一种创新的方法论和方案,预示着在物流及配送问题中的广泛应用前景。