1.曲面定义
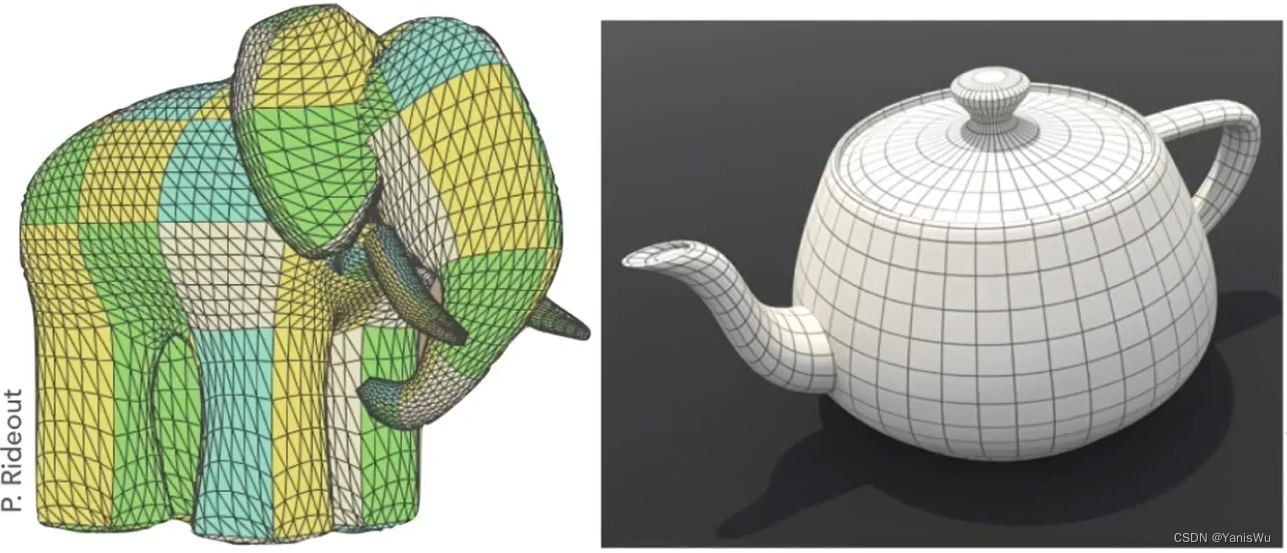
曲面(Surface)在图形学中应用非常广泛,可以用它来描述各种三维物体的表面。如下图所示。
2.贝塞尔曲面
2.1 介绍
曲线和曲面一样都是物体显示的表示方法,自然可以把曲线的概念延伸到平面上。如上图所示,就是贝塞尔曲面(Bezier Surface)构成的表面,并且可以看到是分段面拼接的。
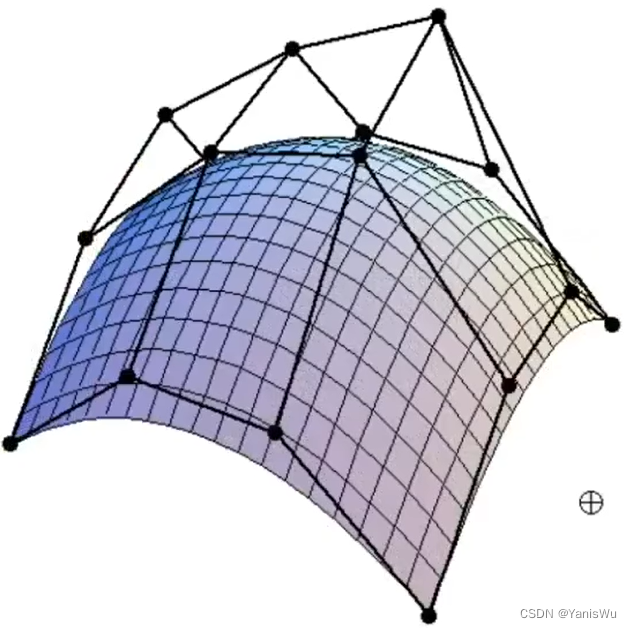
如果对完整的表面进行分解,如上图所示,展示了空间中 4 x 4 个控制点所构成的贝塞尔曲面。贝塞尔曲线控制点都是在同一平面内,那么贝塞尔曲面的控制点则是分部在三维空间中。
2.2 绘制算法
贝塞尔曲面的绘制算法本质上还是基于 De Casteljau's Algorithm 进行多次绘制。如下图所示,首先基于预设的所有控制点(比如:4 x 4 的控制点),绘制 4 条贝塞尔曲线(灰色线)。然后在与曲线垂直的平面中开始绘制曲线,以 4 条贝塞尔曲线上的点作为控制点(输入一个时间 t ),绘制贝塞尔曲线(蓝色线)。

以此类推(给定另外时间 t ) ,不断地输入控制点,最终得到一个贝塞尔曲面。如下图所示。

那么不同的贝塞尔曲面如何拼接在一块?
2.3 计算(u,v)对应的曲面位置
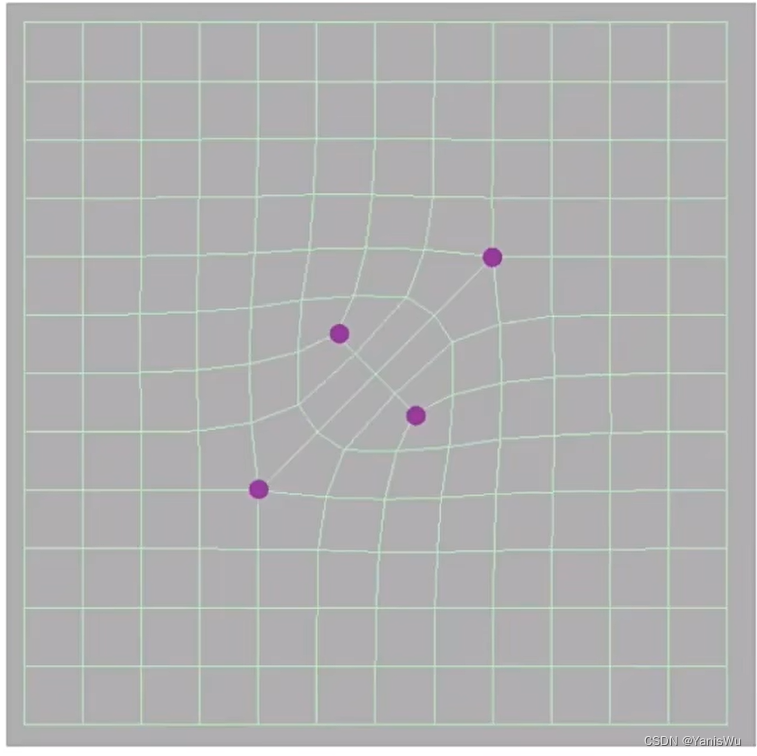
在上述绘制贝塞尔曲面中,需要两个不同的时间 t ,在绘制水平面上需要一个时间 t 绘制四条赛贝尔曲线。然后找到 4 个控制点后连成曲线,还需要一个时间 t 绘制。也就是说需要一个二维的数值去控制,可以用[u,v]去表示。如下图所示。

这样就可以用某一个u沿着四条贝塞尔曲线找到时间u的位置,这样得到四个蓝色的点。再输入v,在蓝色曲线上找到时间v。这样就找到了一个点(u,v),这个点就是曲面在参数u,v下面的位置。那么就可以得到在参数u,v都在0-1范围内,就可以映射成曲面上的任何一个点。如下图所示。
这也说明贝塞尔曲线是显式几何表示,因为是通过参数映射过去的。
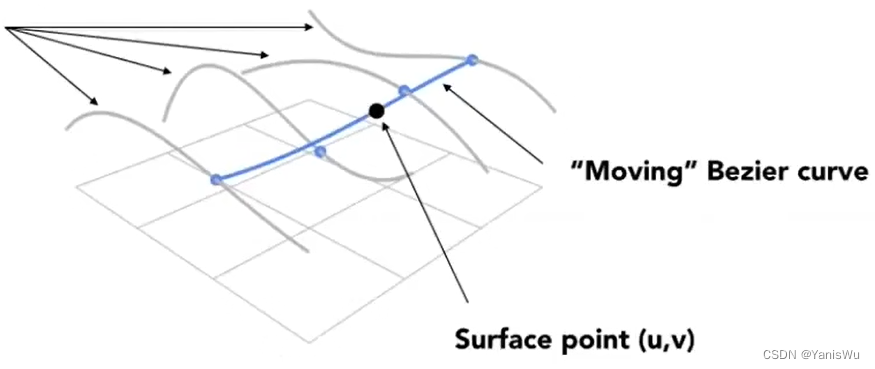
使用(u,v)可以映射曲面上的任何一点,所以在四条曲线上分别得到一个点,再连成一条新的曲线。遍历所有的 u,v值就可以成功得到一个贝塞尔曲面。如下图所示。

3.网格处理
根据上述绘制算法,我们可以得到基于多边形网格的曲面,一般网格都是三角形组成。在实际应用中,我们会对曲面形成的网格进行进一步的处理。常见的曲面处理操作:网格细分(Mesh Subdivision)、网格简化(Mesh Simplification)和网格正规化(Mesh Regularization)。

3.1 网格细分
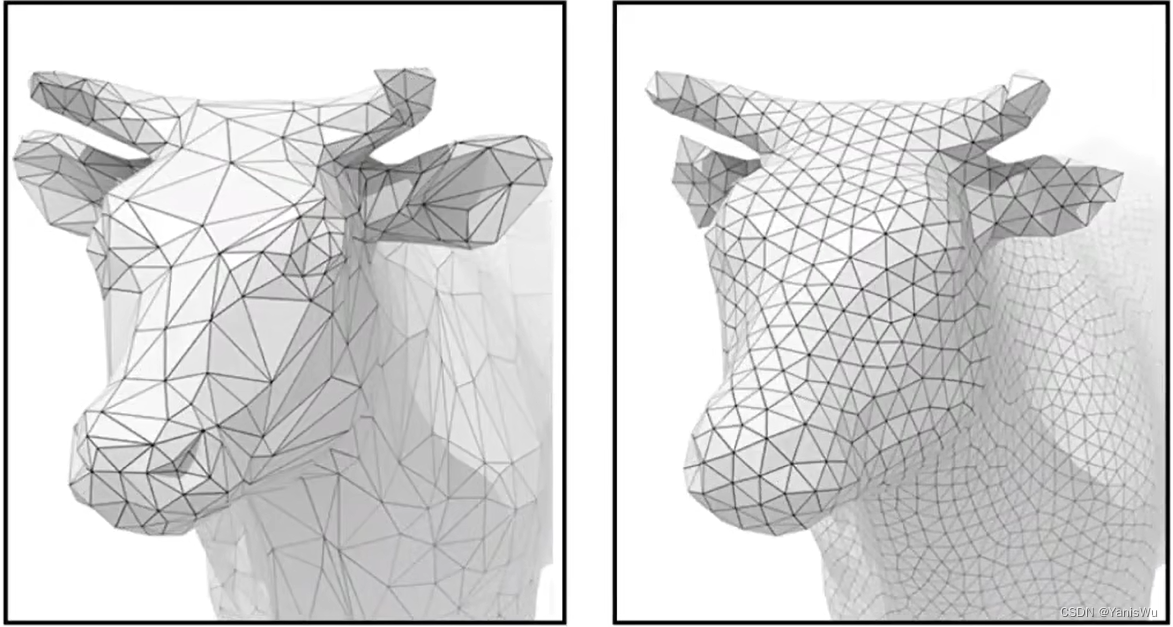
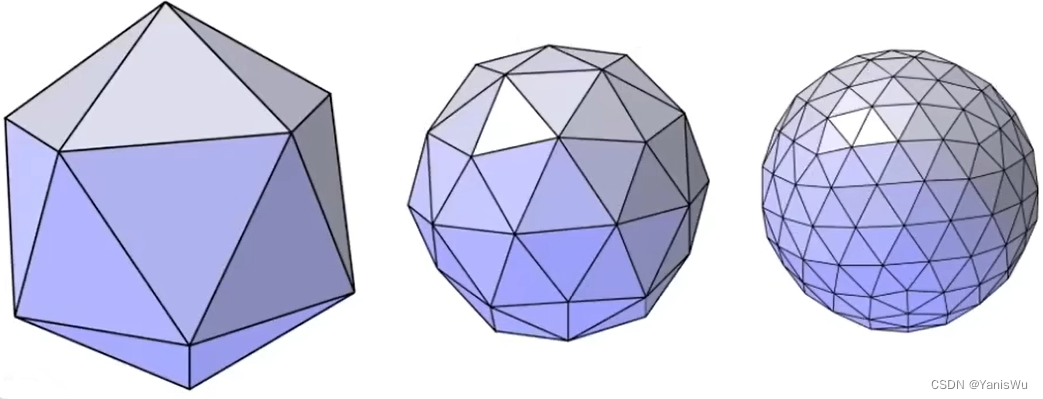
网格细分就是把一个多边形拆分成多个多边形,其目的是增加三角形数量,细节更加丰富,表面更加光滑。如下图所示。

网格细分又可分为Loop细分和Catmull-Clark细分。
3.1.1 Loop细分
Loop细分是三角网格常用的细分规则。主要有两步操作,首先拆分出更多的三角形(顶点),然后移动三角形的位置,使表面变得光滑。如下图所示。注意:这里loop不是循环的意思,是发明人的名字。
1.将一个三角形拆分四个
连接三角形每条边的中点,即可将拆分成四个三角形。如下图所示。
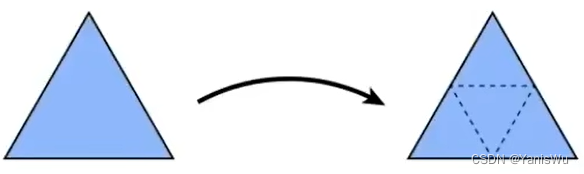
2.根据权重分配新的位置,使表面平衡。
将顶点分为旧顶点和新顶点,新顶点就是拆分三角形取中点的点,旧顶点就是原三角形的顶点。对于这两种不同的顶点,分别用不同的规则改变位置。
对于新顶点的位置更新,如下图白点举例,基于周围四个旧顶点求加权平均,离它近的顶点权重大,设为 3/8,离它远的顶点权重小,设为 1/8。如下图右侧公式所示计算白点位置,其他新顶点同理求得。

对于旧顶点的位置更新,如下图白色点为例。

基于周围几个旧顶点求加权平均,其中各个点的权重值与待更新点(白点)的度(Degree)有关,顶点的度是指这个顶点连接的边的数量。
在这里我们定义一个n,为顶点的度。再定义一个u,这个u仅仅是一个与顶点的度有关的数。最终的计算公式如下:
![]()
从这个公式可以看到,当顶点的度很大(连接了很多三角形),那么这个顶点基本就可以由周围的旧顶点决定位置,当顶点的度很小(连接的三角形很少),那么这个顶点原来位置的权重就会很大。
以上就是Loop细分的全过程了,如下图所示是做两次loop细分的例子。
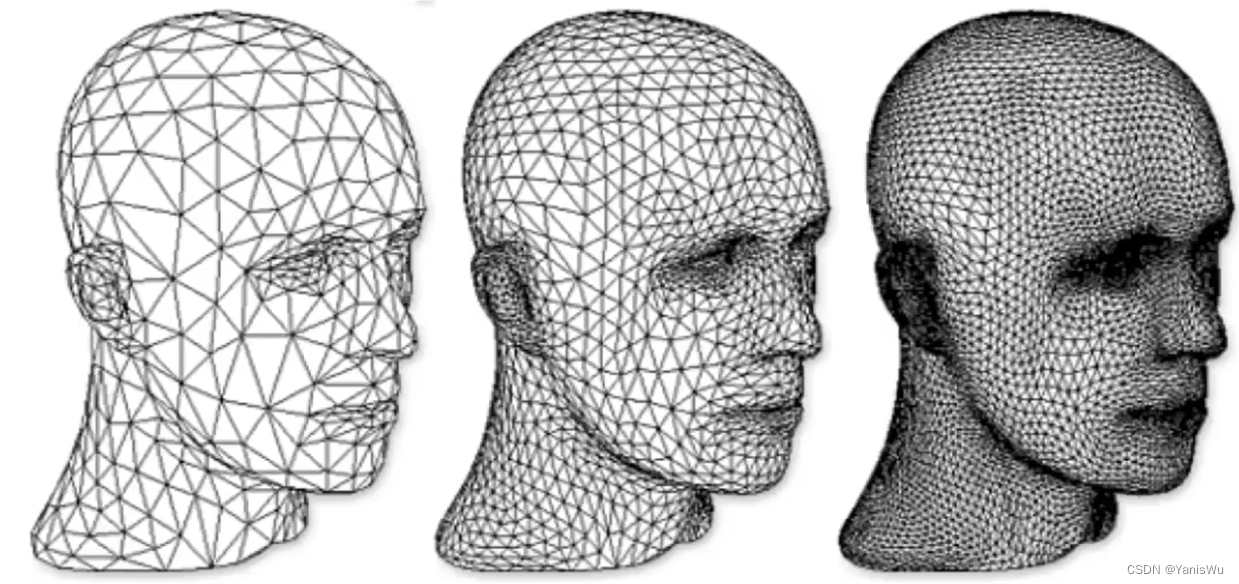
Loop细分只针对三角形面进行细分。如下图是一个不断进行Loop细分的例子。
3.1.2 Catmull-Clark细分
正如上文所说Loop细分针对是所有三角形面,那么对于不仅仅只有三角形面该怎么办呢?这也就有了Catmull-Clark细分。与loop细分同理,Catmull-Clark细分也是先增加顶点,再移动顶点位置。
接下来看如何做Catmull-Clark细分,这里以四边形面和三角面的混合为例,先定义两个概念。如下图所示。
1.对于所有不是四边形的面,称之为Non-quad face。
2.所有度不为4的顶点称之为奇异点。

每次细分步骤:在每个面中心都添加一个顶点,在每条边的中点也都添加一个点,面中心的新顶点连接所有边上的新顶点,结果如下图所示。
经过一次细分后,有以下几个问题。
1.现在还有几个奇异点?
2.这些奇异点的度是多少?
3.有多少个Non-quad face?
考虑这几个问题,其实也是一些Catmull-Clark细分的特点
1.有几个非四边形面,就会多出几个奇异点,原本的面是非四边形那么中间一定会出现一个奇异点。所以现在一共有2+2 = 4个。
2.新多出来的奇异点的度数与原来所在面的边数相等,原来奇异点的度不变。所以新奇异点就是3度,原来的奇异点还是5度。
3.第一次细分之后所有非四边形面都会变成四边形,且往后奇异点数目不再增加,所以是0个。
这里再做一次细分,结果如下图所示。
可以看到奇异点依然是4个,不再改变。
以上进行了增加顶点,那么接下来如何对顶点进行位置更新呢?
这里将所有顶点的更新分为三种,第一种是对于面的中心点 f 的更新,第二种是对于边的中心点 e 的更新,第三种是对于老的顶点 v 的更新。
对于各类顶点位置调整如下图所示。

3.1.3 Loop细分与Catmull-Clark细分的区别
loop细分只能做三角面的细分,而Catmull-Clark细分可以做各种不同面的细分。
3.2 网格简化
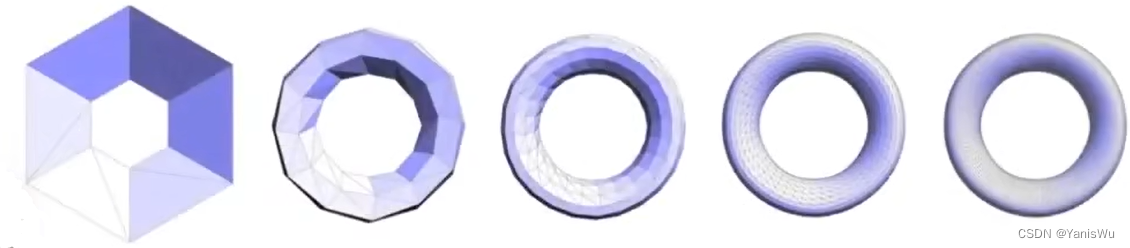
网格简化是网格细分的逆过程,其目的是为了减少三角形数量,从而提升性能。在实际应用中,一些距离很远的物体不需要丰富的细节,可以进行网格简化。如下图所示。

3.2.1 网格简化算法
曲面简化的目的是在保持整体造型的同时减少网格元素的数量。如下图所示,一个模型从3万个顶点到30个顶点的过程,可以看到细节是越来越差的。

如下图所示,当模型距离很远或者很小的时候,3万个顶点与3千个顶点看上去差别并不大,顶点多浪费了性能开销,就需要简化。

那么,怎么样去计算这个过程?
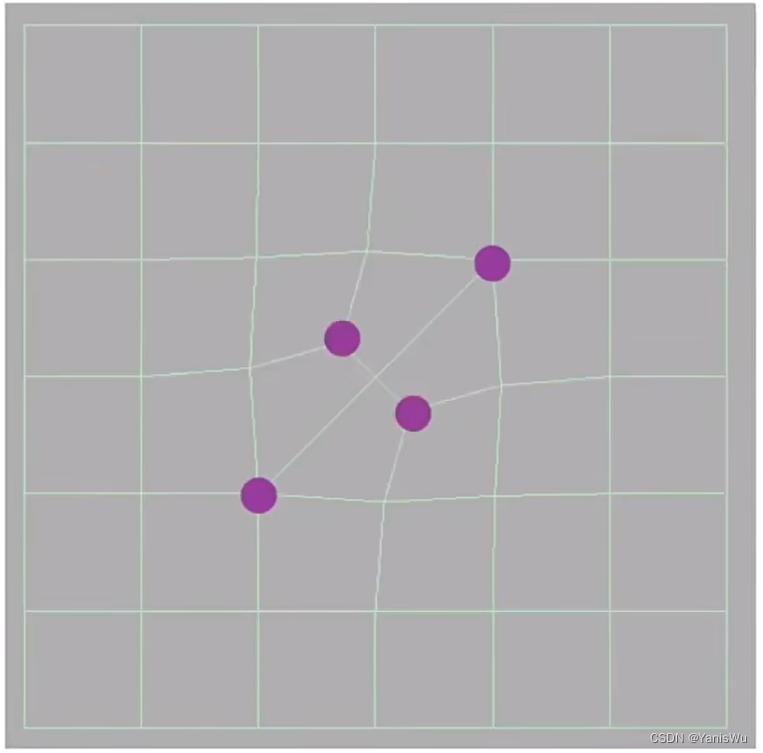
曲面简化所利用的一个方法叫做边坍缩(Edge Collapse)。如下图所示,就是将一条边的两个顶点合成为一个顶点。
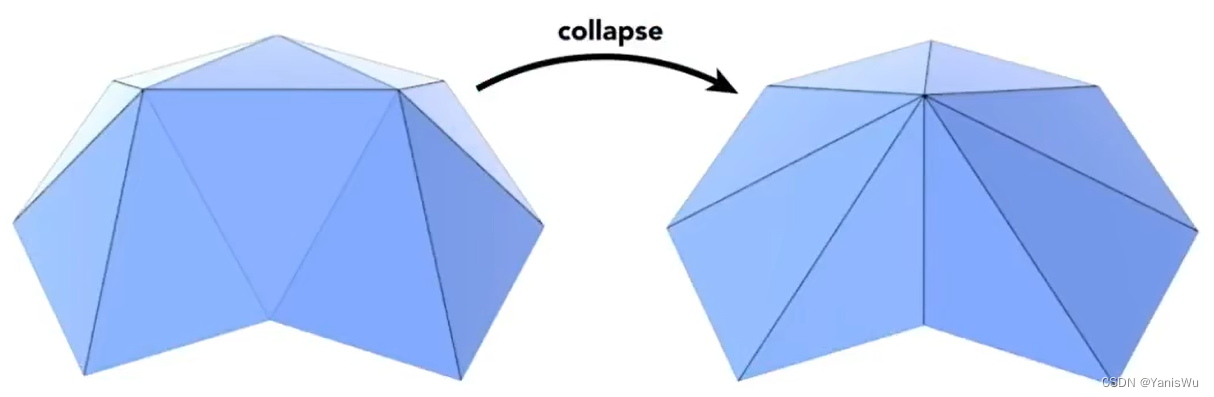
但随之而来的问题就是,曲面简化需要尽量保持原本模型的基本轮廓,如何坍缩一条边,或者说坍缩哪一条边能够使得原模型样貌被改变的程度最小,这就是曲面简化的关键所在。
如下图所示,是一个将中间三个顶点简化成一个顶点的位置,先做了一次平均处理得到的结果。可以发现得到新的三角形无论如何都比原来的面小,那肯定是不对的。

为此引入一个误差的度量,即二次误差度量(Quadric Error Metrics)。

把这个新生成的顶点放置在某个位置上,使得这个顶点到原来相关联的各个面的距离的平方和达到最小(上图中的边代表三角面)。如果能够使得这个误差最小那么对整个模型样貌修改一定程度上也会较小。
对于整个模型有很多条边,假设如果坍缩一条边,并且算出把这个坍缩后的点放在最佳的位置上会得到一个多大的二次度量误差?对于整个模型而言,每次肯定都是要坍缩二次度量误差最小的边开始。
综上,这整个曲面简化的算法流程如下。
1.为模型每条边赋值,其值为坍缩这条边之后,代替两个老顶点的新顶点所能得到的最小二次误差度量。
2.选取权值最小的边做坍缩,新顶点位置为原来计算得出使得二次误差最小的位置。
3.坍缩完之后,与之相连其他的边的位置会改动,更新这些边的权值。
4.重复上述步骤,直到到达终止条件
但是问题是,如果坍缩了一条边,会有一些临近边的位置要跟着这条坍缩的边变化,那么这些边的二次度量误差就会随之发生变化。
因此这里要通过一种数据结构,既可以每次取到二次度量误差的最小值的边,又可以动态地以最小的代价去更新其他的受影响的元素。那么这里要使用的数据结构就是堆(优先队列),允许求最小,并且运行时动态更新任何一点的值。
在任意一个局部(任意一个位置一条边)附近都找最优的做法,通过不断找局部最优的方式来找全局的最优解。这其实是一个标准的贪心算法,可能到不了全局最优解,但事实证明最终的结果依然相当不错,如下图所示。

3.3 网格正规化
网格正规化就是让三角形不至于出现特别尖、特别长的三角形,变成接近正三角形相似的三角形。需要注意的事,在改善三角形质量的同时不能丢失模型本身的质量。如下图所示。