【因果推断python】50_去偏/正交机器学习2

news2024/11/27 22:26:48

Frisch-Waugh-Lovell on Steroids

CATE Estimation with Double-ML

Frisch-Waugh-Lovell on Steroids

双重/偏差 ML 其思想非常简单：在构建结果和治疗残差时使用 ML 模型：

$Y_i-\hat{M}_y(X_i)=\tau\cdot(T_i-\hat{M}_t(X_i))+\epsilon$

$\hat{M}_y(X_i)$ 是估计 $E[Y|X]$ ， $\hat{M}_t(X_i)$ 是估计 $E[T|X]$

我们的想法是，ML 模型具有超强的灵活性，因此在估计 Y和 T残差，同时仍然保持 FWL 风格的正交化。这意味着我们不必对协变量 X与结果 Y或协变因素与治疗之间的关系作出任何参数假设，以获得正确的治疗效果。只要没有未观察到的混杂因素，我们就可以通过以下正交化程序计算ATE：

1.估计结果 Y 使用特征 X, 使用灵活的 ML 回归模型 $M_{y}$
2.估计治疗 T 利用特征 X,使用灵活的 ML 回归模型 $M_{t}$
3.获取残差 $\tilde{Y}=Y-M_y(X)$ 和 $\tilde{T}=T-M_t(X)$
4. 将结果的残差与处理的残差进行回归 $\tilde{Y}=\alpha+\tau\tilde{T}$

$\tau$ 就是ATE，我们可以用 OLS 对其进行估计。ML 的强大之处在于灵活性。ML 功能强大，可以捕捉干扰关系中复杂的函数形式。但这种灵活性也带来了麻烦，因为这意味着我们现在必须考虑过度拟合的可能性。

Chernozhukov 等人（2016 年）对过度拟合如何造成问题进行了更深入、更严谨的解释，我强烈建议您去看看。但在这里，我将基于直觉进行解释。

要了解这个问题，假设您的 $M_{y}$ 模型正在过度拟合。其结果是残差 Y 将小于其应有的值。这也意味着 $M_{y}$ 所捕捉的不仅仅是 X 和 Y 之间的关系，其中还有一部分是 T 和 Y 之间的关系，如果 $M_{y}$ 捕捉到了其中的一部分，那么残差回归将偏向于零。换句话说、 $M_{y}$ 正在捕捉因果关系，而不是将其留给最终的残差回归。

现在来看看过度拟合 M 的问题，注意它对 T 方差的解释将超过它应该解释的方差。因此，T残差的方差会小于其应有的方差。如果处理的方差较小，最终估计值的方差就会很大。这就好比几乎每个人的待遇都是一样的。如果每个人的治疗水平都相同，那么就很难估计不同治疗水平下的情况。另外，当 T是 X 的确定性函数时，也会出现这种情况，这意味着违反了positivity 。

这些就是我们在使用 ML 模型时遇到的问题，但我们如何才能纠正这些问题呢？答案就在于我们所说的交叉预测和折外残差。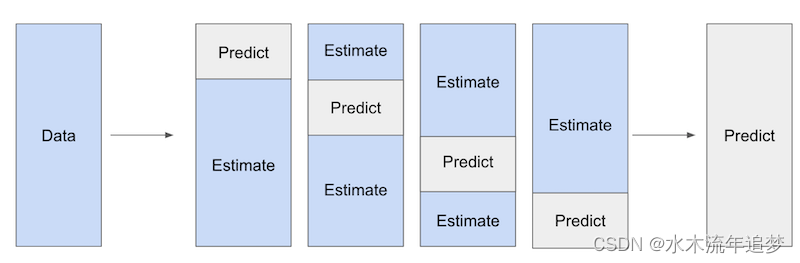

我们将把数据分成大小相等的 K 部分。然后，对于每个 K 部分，我们将在所有其他 K-1 个样本上估计 ML 模型，并得出 K 部分的残差。请注意，这些残差是通过折外预测得出的。我们在一部分数据上拟合模型，但在另一部分数据上进行预测和计算残差。

因此，即使模型拟合过度，也不会人为地将残差推向零。最后，我们综合所有 K 部分的预测结果，估计出最终的因果模型 $\tilde{Y}=\alpha+\tau\tilde{T}$ .

好了，我们已经讲了很多，如果不举例说明，可能很难跟上。为了配合这些理论，让我们一步一步来实现双重/偏差 ML。在此过程中，我将借此机会解释每个步骤的作用。

首先，让我们使用 ML 模型来估计干扰关系。我们将使用一个 LGBM 模型，根据协变量温度、工作日和成本来预测价格。这些预测将是交叉预测，我们可以使用 sklearn 的 cross_val_predict 函数来获得。我还将平均 $\hat{\mu}_{t}$ 以实现可视化。

from lightgbm import LGBMRegressor
from sklearn.model_selection import cross_val_predict

y = "sales"
T = "price"
X = ["temp", "weekday", "cost"]

debias_m = LGBMRegressor(max_depth=3)

train_pred = train.assign(price_res =  train[T] -
                          cross_val_predict(debias_m, train[X], train[T], cv=5)
                          + train[T].mean()) # add mu_t for visualization.

请注意，我把 $M_{t}$ 模型称为debias 模型。这是因为该模型在 Double/Debias ML 中扮演的角色是使治疗去偏。残差 $\tilde{T}=T-M_t(X)$ 可以看作是治疗的一个版本，在这个版本中模型已经消除了 X 带来的所有混杂偏差。换句话说， $\tilde{T}$ 与 X 是正交的。因为它已经被 X 解释过了。

为了说明这一点，我们可以展示我们之前看到的同一幅图，但现在用价格残差代替了价格。还记得之前周末的价格更高吗？现在，这种偏差消失了。所有工作日的价格残差分布都是一样的。

np.random.seed(123)
sns.scatterplot(data=train_pred.sample(1000), x="price_res", y="sales", hue="weekday");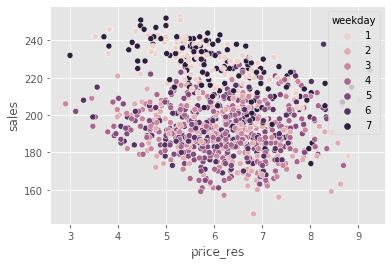

$M_{t}$ 的作用是消除T 的偏差，但 $M_{y}$ 又是什么呢？它的作用是去除 Y 的方差。直观地说， $M_{y}$ 创造了一个outcome版本，在这个版本中，由 X 引起的所有方差都被解释掉了。这样一来，对 $\tilde{Y}$ 的因果关系进行估计就变得更容易了。由于噪音较小，因果关系变得更容易看清。

np.random.seed(123)
sns.scatterplot(data=train_pred.sample(1000), x="price_res", y="sales_res", hue="weekday");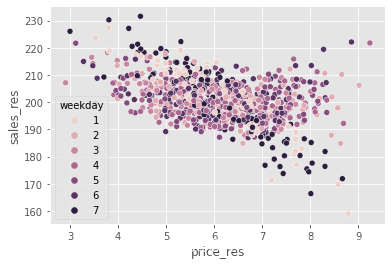

现在，我们不难看出价格与销售额之间的负相关关系。

最后，为了估计这种因果关系，我们可以对残差进行回归。

final_model = smf.ols(formula='sales_res ~ price_res', data=train_pred).fit()
final_model.summary().tables[1]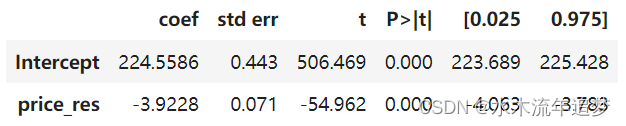

我们可以看到，当我们使用销售额和价格的残差或正交化版本时，我们可以非常确信价格和销售额之间的关系是负的，这非常有意义。当我们提高价格时，冰淇淋的需求量就会下降。

但是，如果我们看一下价格与销量之间的未重构关系或原始关系，由于存在偏差，我们会发现两者之间存在正相关关系。这是因为，在预期高销售量的情况下，价格会提高。

final_model = smf.ols(formula='sales ~ price', data=train_pred).fit()
final_model.summary().tables[1]

CATE Estimation with Double-ML

到目前为止，我们已经了解了双重/偏差 ML 如何让我们专注于估计平均治疗效果 (ATE)，但它也可用于估计治疗效果异质性或条件平均治疗效果 (CATE)。从本质上讲，我们现在说的因果参数 $\tau$
会随单位协变量的变化而变化。

$Y_i-M_y(X_i)=\tau(X_i)\cdot(T_i-M_t(X_i))+\epsilon_i$
为了估计这一模型，我们将使用相同的价格和销售额残差，但现在我们将价格残差与其他协变量进行交互。然后，我们可以拟合一个线性 CATE 模型。

$\tilde{Y}_{i}=\alpha+\beta_{1}\tilde{T}_{i}+\boldsymbol{\beta}_{2}\boldsymbol{X}_{{\boldsymbol{i}}}\tilde{T}_{i}+\epsilon_{i}$
估算出这样一个模型后，为了进行 CATE 预测，我们将使用随机测试集。由于这个最终模型是线性的，因此我们可以机械地计算 CATE, M是我们最终的模型。

$\hat{\mu}(\partial Sales_i,X_i)=M(Price=1,X_i)-M(Price=0,X_i)$

final_model_cate = smf.ols(formula='sales_res ~ price_res * (temp + C(weekday) + cost)', data=train_pred).fit()

cate_test = test.assign(cate=final_model_cate.predict(test.assign(price_res=1))
                        - final_model_cate.predict(test.assign(price_res=0)))

为了检验该模型在区分价格敏感度高的单位和价格敏感度低的单位方面的效果如何，我们将使用累积弹性曲线。

gain_curve_test = cumulative_gain(cate_test, "cate", y=y, t=T)
plt.plot(gain_curve_test, color="C0", label="Test")
plt.plot([0, 100], [0, elast(test, y, T)], linestyle="--", color="black", label="Baseline")
plt.legend();
plt.title("R-Learner");