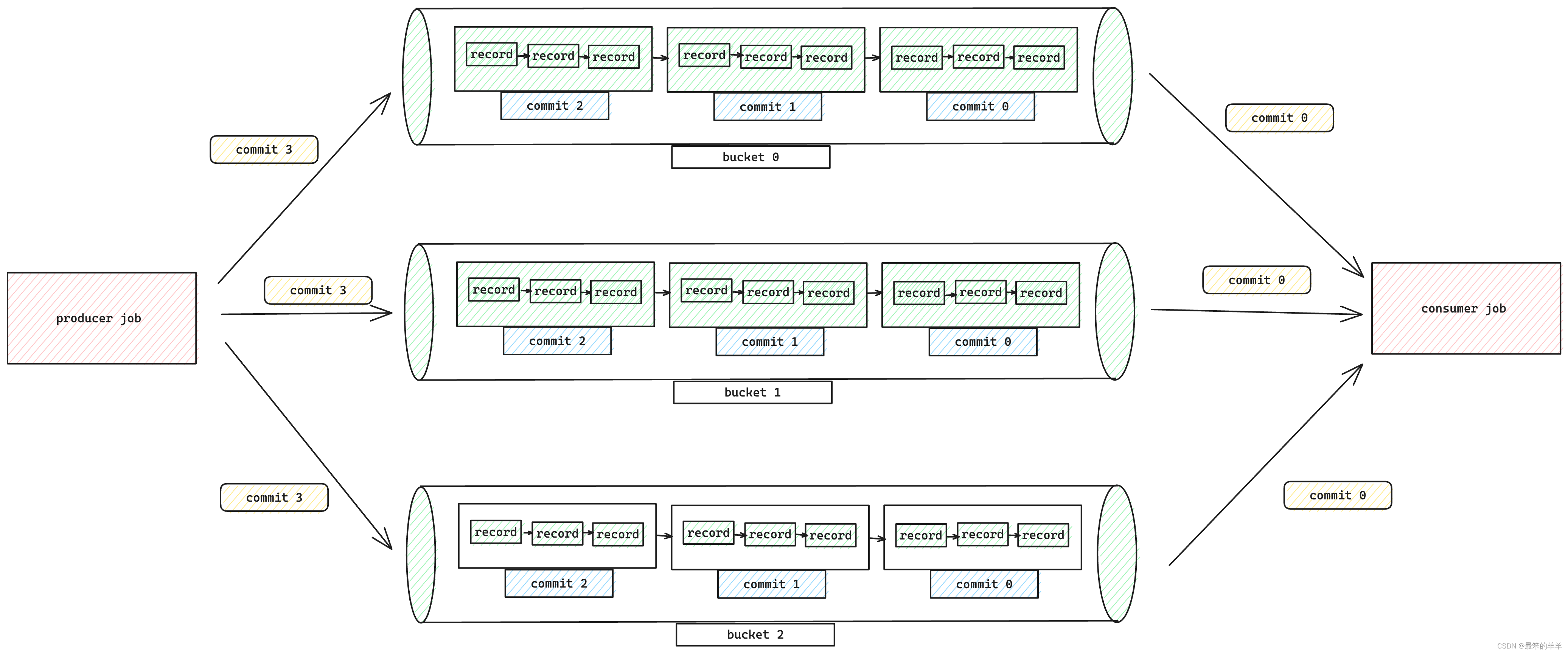
B(B-)树定义
B树(或B-tree)是一个在计算机科学中广泛使用的数据结构,它是一种自平衡的树,能够保持数据有序。
以下是B树的特性
- 每个节点最多右m个孩子,二叉树是B-树的特例,其有2个孩子。
- 除了叶节点和根节点以外,每个内部节点至少有Math.ceil(m/2)个孩子。
- 如果根不是叶节点,则至少有两个孩子。
- 所有叶节点都出现在一层,也就是说从根到叶节点点的度(层,高度)一样。
- 具有K个孩子的非叶节点包含 K-1个数据,在节点内部的键值是递增的。
B树模型
B-树节点
B树的阶: B树的节点(除根节点外) 最多 有多少个孩子结点(子树),一般用字母 M 表示阶数。
如果所示节点可以连接4个树,此树为四阶B树。
每个节点中存储的数据最多不超过M-1 = 3;
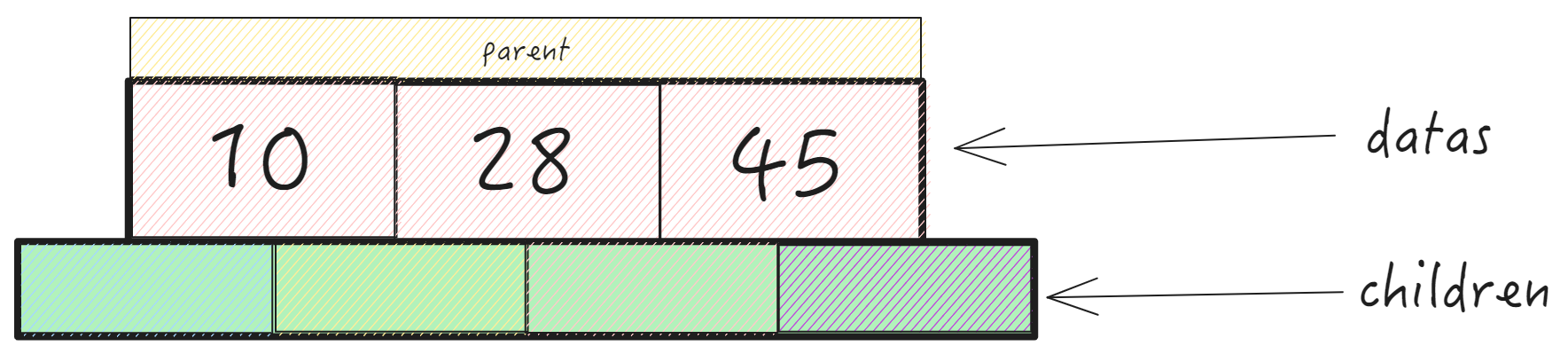
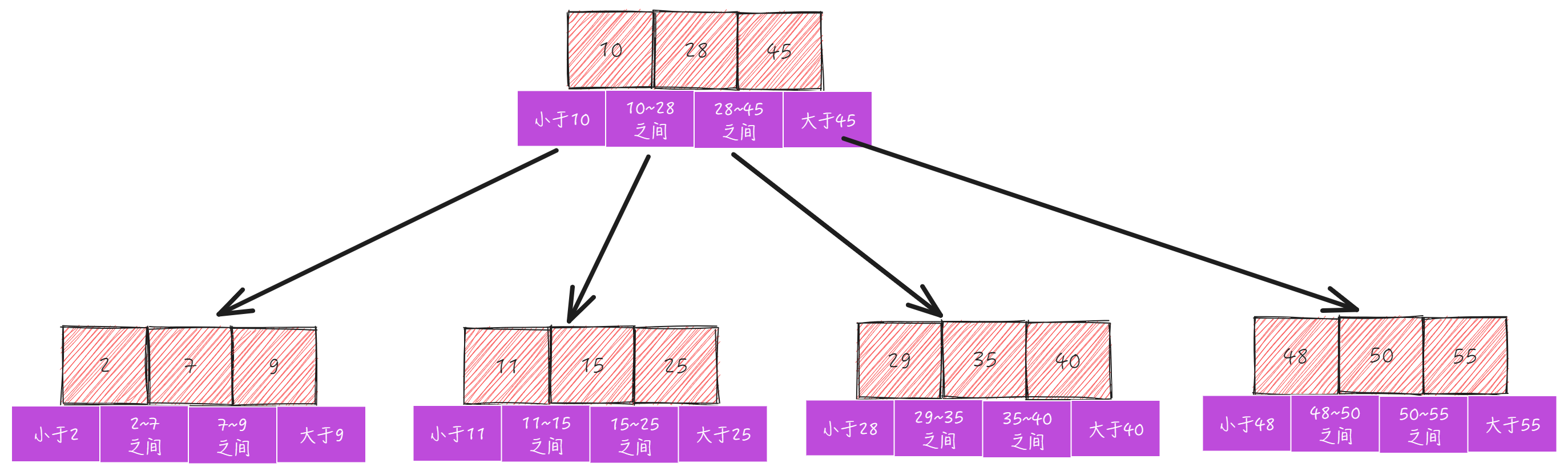
B-树的一般结构
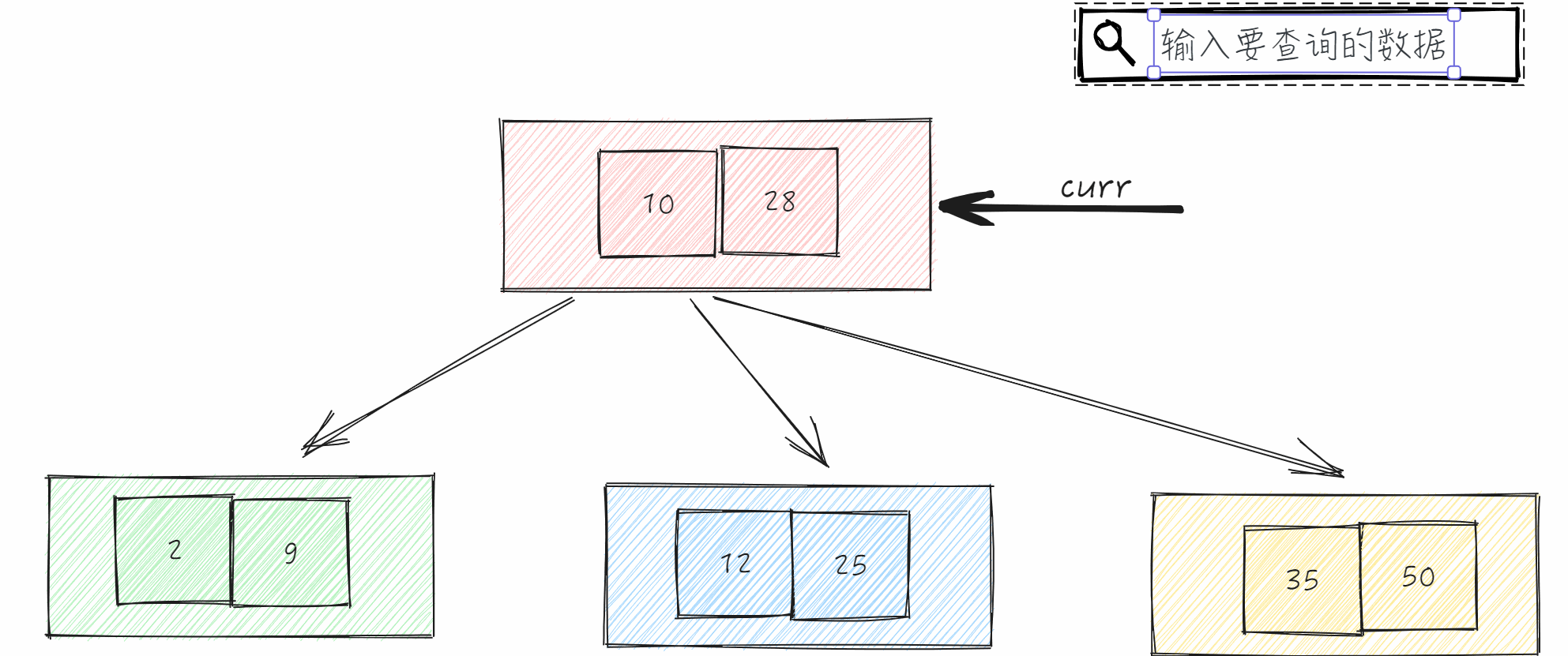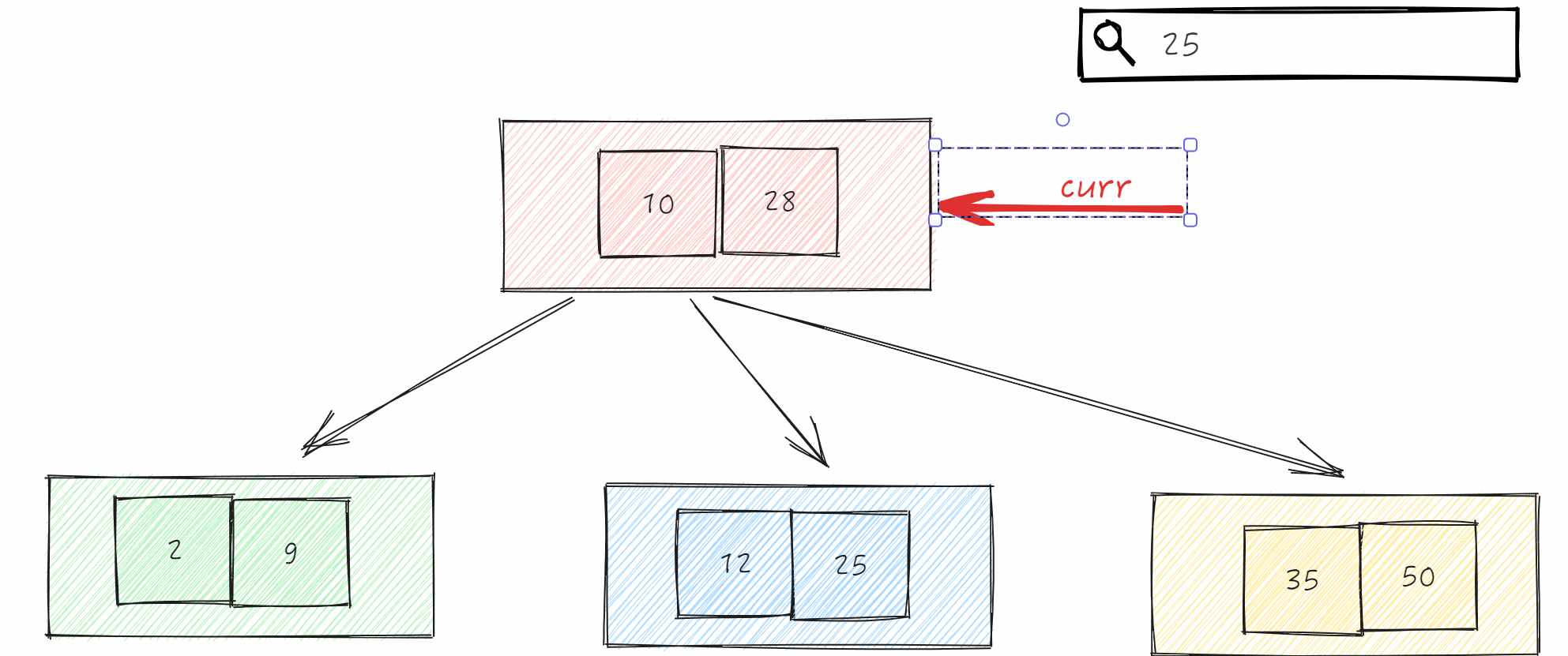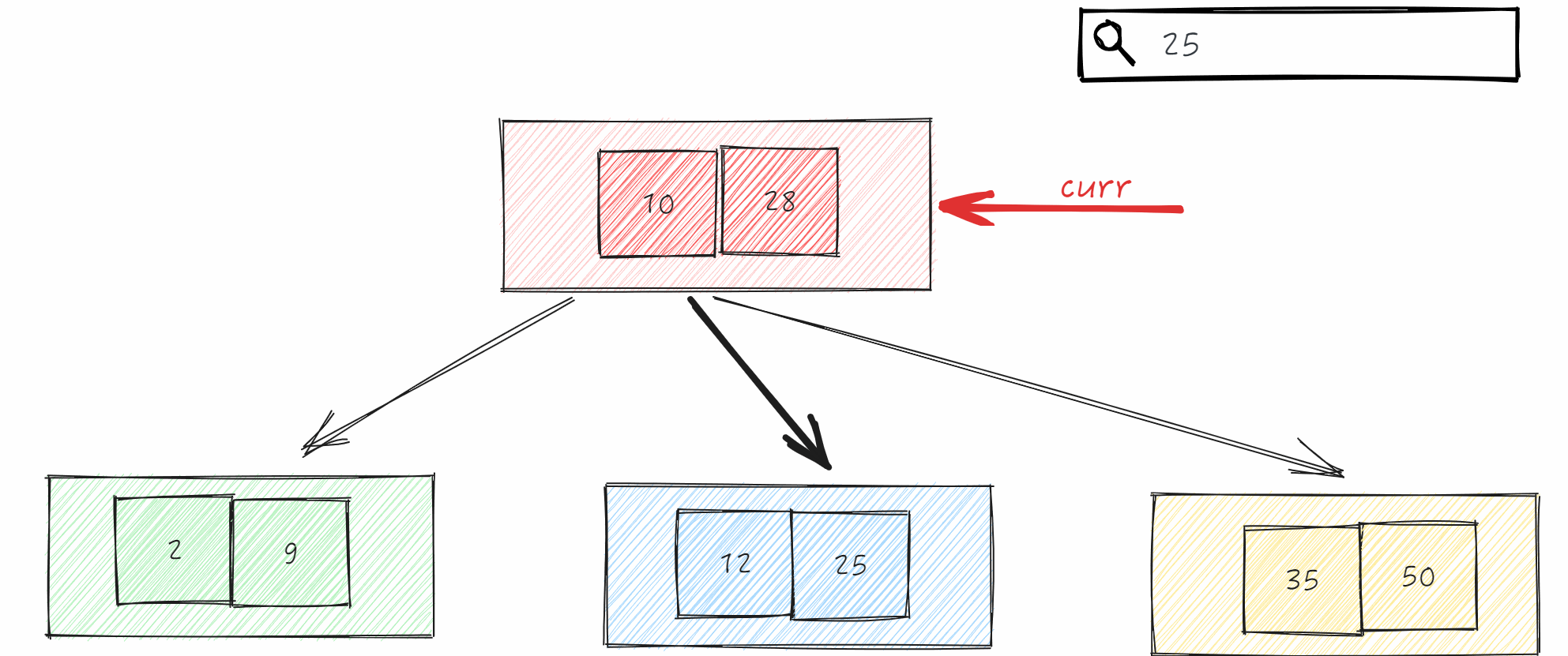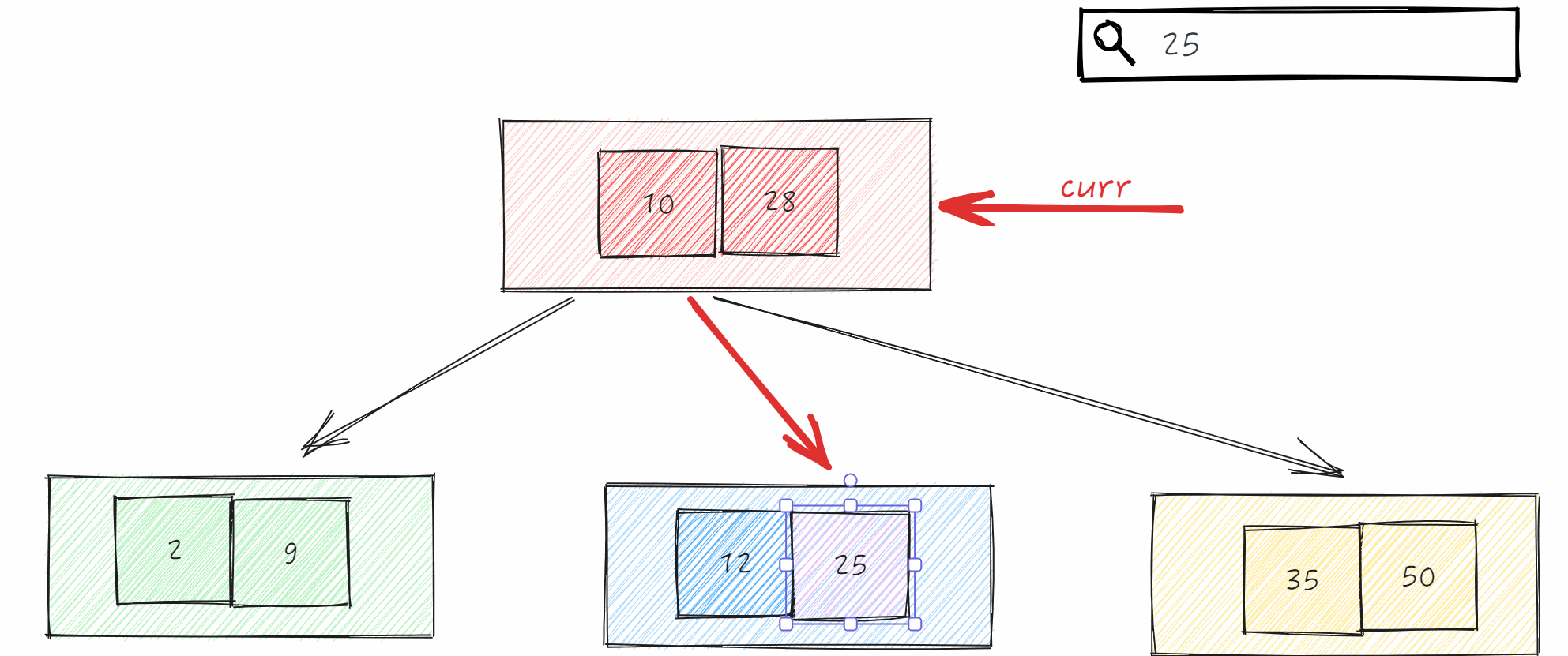
查询
查询在B-树中数据,如果能找到我们需要知道节点对象和节点中哪个位置(每个节点内存储多个数据)
如果没有查询到我们需要记录当前的节点对象及位置为-1(表示不存在)。
NodeBind类
定义一个NodeBind类包装节点和数据的位置。
/**
* 绑定数据在节点中位置类
*/
public class NodeBind {
private Node node; //当前节点
private int index; //当前节点中数据的位置
public Node getNode() {
return node;
}
public void setNode(Node node) {
this.node = node;
}
public int getIndex() {
return index;
}
public void setIndex(int index) {
this.index = index;
}
public NodeBind(Node node, int index) {
this.node = node;
this.index = index;
}
@Override
public String toString() {
return "Pair{" +
"node=" + node +
", index=" + index +
'}';
}
}
查询实现
从根节点开始遍历,先从根节点开始检查是否存有要查找的数据,如果找到则返回Pair对象,如果没有则记录最后一个扫描到的对象,将其包装为Pair对象返回。
/**
* 查询data在B树的节点位置
*
* @param data
* @return
*/
public Pair search(int data) {
Node curr = root;
Node parent = null;
while (curr != null) {
int rowIndex = 0;
while (rowIndex < curr.size) {
List<Integer> datas = curr.datas;
int index = datas.indexOf(data);
if (index != -1) {
return new Pair(curr,index);
} else if (data > datas.get(rowIndex)) {
rowIndex++;
} else {
break;
}
}
parent = curr;
curr = curr.children.get(rowIndex);
}
return new Pair(parent,-1);
}
添加数据
我们采用的策略是先暂时存储数据,当存入后数据超出其长度进行分裂处理。
辅助方法指定节点添加数据
private void insertBySort(Node node, int data) {
int index = node.size;
for (int i = 0; i < node.datas.size(); i++) {
if (data < node.datas.get(i)) {
index = i;
break;
}
}
node.datas.add(index, data);
node.size++;
}
添加新数据
我们向B树中添加数据{12,45,9,78,80,5,3,79,20},跟踪B树的添加过程。
添加第一个元素12
创建新节点即为root节点,在datas中存入数据12。

if (root == null) {//如果根节点不存在
root = new Node();
root.datas.add(data);
root.size++;
return;
}
添加数据45
在根节点的第二个位置添加45,找到要添加的节点。 节点的数据安装升序排序存放。

/*
从B-树中查找节点是否存在
*/
Pair findNode = search(data);
//数据已经在B树中,只更新不插入
if (findNode.getIndex() != -1) return;
/*
如果没有找到则插入节点
- 当前要插入的节点没有满
- 当前要插入的节点已满,需要分裂节点
*/
Node curr = findNode.getNode();
insertBySort(curr, data);
if (curr.size <= M - 1) { //如果当前节点的数据没有满,最大存储M-1数据
return;
}
添加数据9
查找位置添加节点,代码和4.2.3一致。

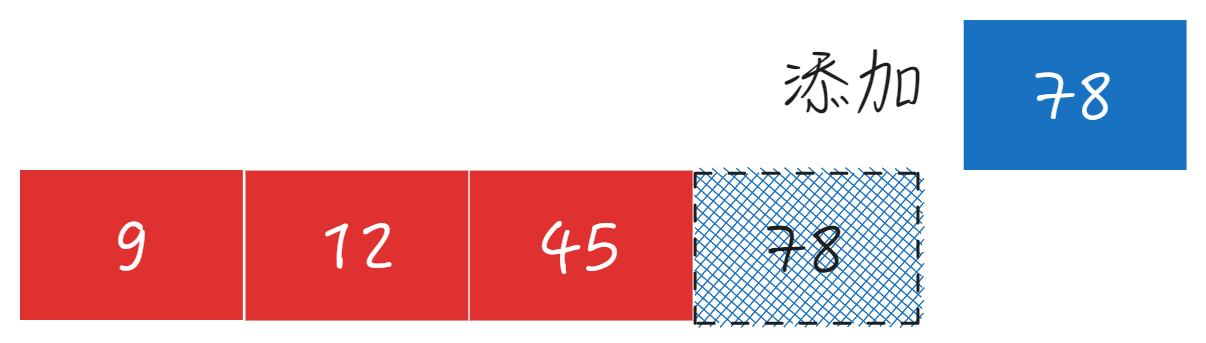
添加数据78
重复添加过程,需要判断当前节点容量是否已满,当前节点的数据容量: size<=M-1
如果超过容量则需要分裂当前节点。
....添加节点代码
if (curr.size <= M - 1) { //如果当前节点的数据没有满,最大存储M-1数据
return;
} else { //当前节点已满
System.out.println("当前节点已满,准备分裂...");
split(curr);
}
分裂节点
以当前节点的中间节点为中心将左右分裂为两个节点
- 原节点保留左侧数据
- 新建节点保留右侧数据
- 如果当前节点为根节点,需要新创建节点为根节点,存储中间节点数据。

public void split(Node curr) {
int mid = curr.size / 2; //找到中间节点
int midVal = curr.datas.get(mid); //记录中间节点的值
Node parent = curr.parent; //记录当前节点的父节点
/*
* 创建新节点,用来存储分裂的右侧节点
*/
Node newNode = new Node();
for (int i = mid + 1; i < curr.size; i++) {
newNode.datas.add(curr.datas.get(i)); //新节点循环添加mid+1开始的节点
newNode.size++; //新节点数据大小更新
curr.datas.remove(i); //删除右侧数据(右侧节点放中间朝右的数据)
i--; //防止引起集合索引的移动(由于删除了数据,集合大小会改变,当前位置也会调整,回退到删除为止)
curr.size--; //当前节点的数据-1处理
}
:
:
}
如果当前节点是根节点,分裂两个子树,实际上当前节点和分裂节点的每一个parent要连接新的parent,parent的每一个孩子节点的孩子节点要引用这两个节点(可以自行完成,繁琐但不难)。
/*
* 判断当前节点是否为根节点
*/
if (parent == null) {//父节点为空,当前节点为根节点
root = new Node();//产生一个新的父节点
root.datas.add(midVal); //拷贝当前节点的中间值到父节点中
curr.datas.remove(Integer.valueOf(midVal)); //从当前对象中移除已经添加到root上的数据
curr.size--;
root.size++; //父节点长度更新
root.children.add(curr); //父节点的孩子节点连接子节点
curr.parent = root; //当前节点的父节点变成新的父节点
root.children.add(newNode); //添加右侧的子节点到父节点的孩子节点中
newNode.parent = root; //右接点的父节点连接新父节点
return;
}
添加80
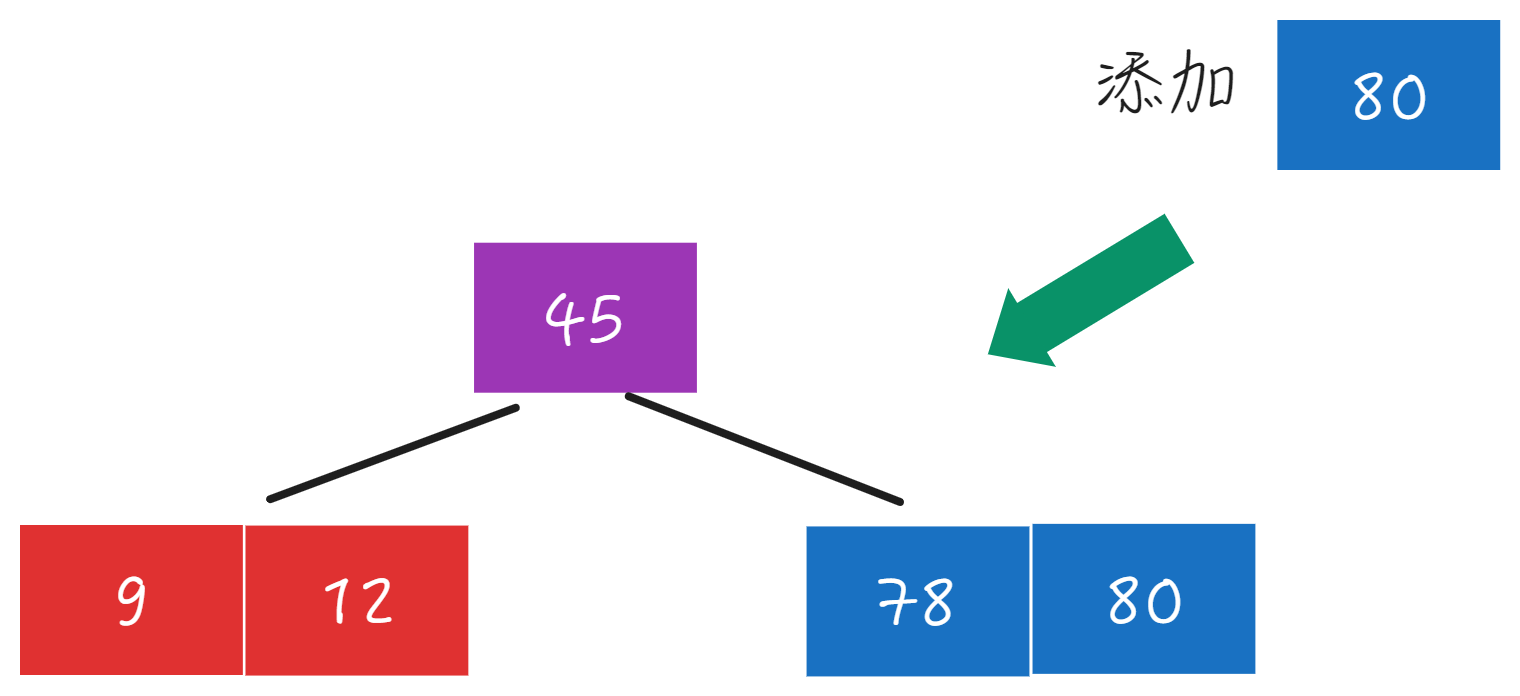
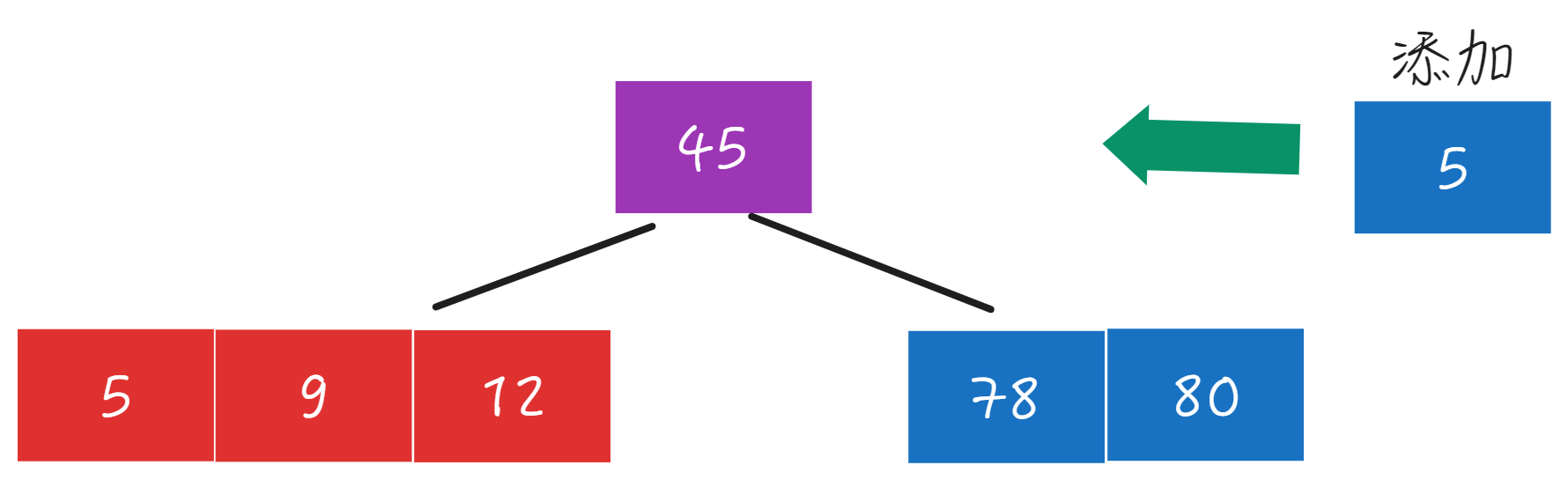
添加5
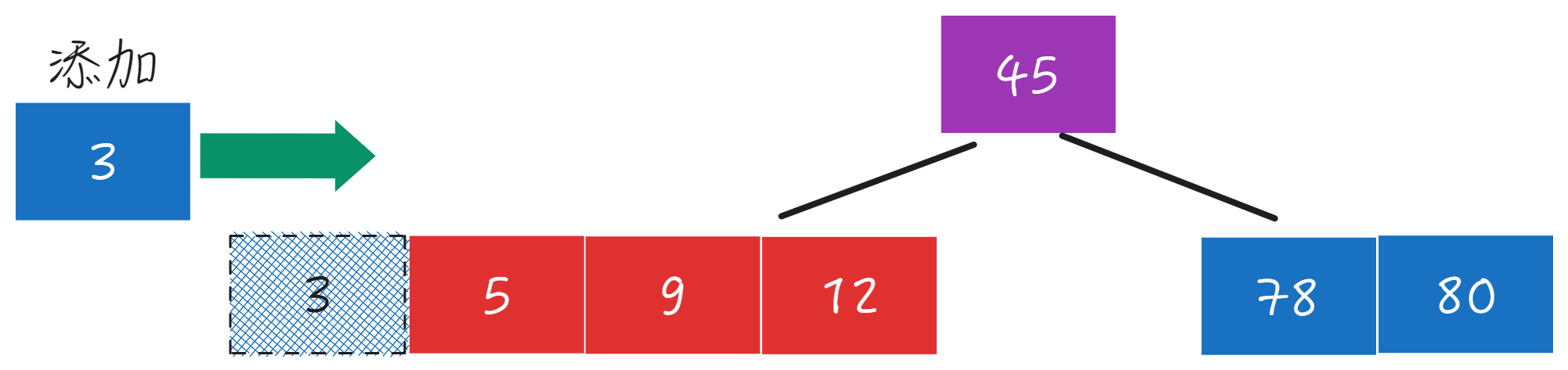
添加3
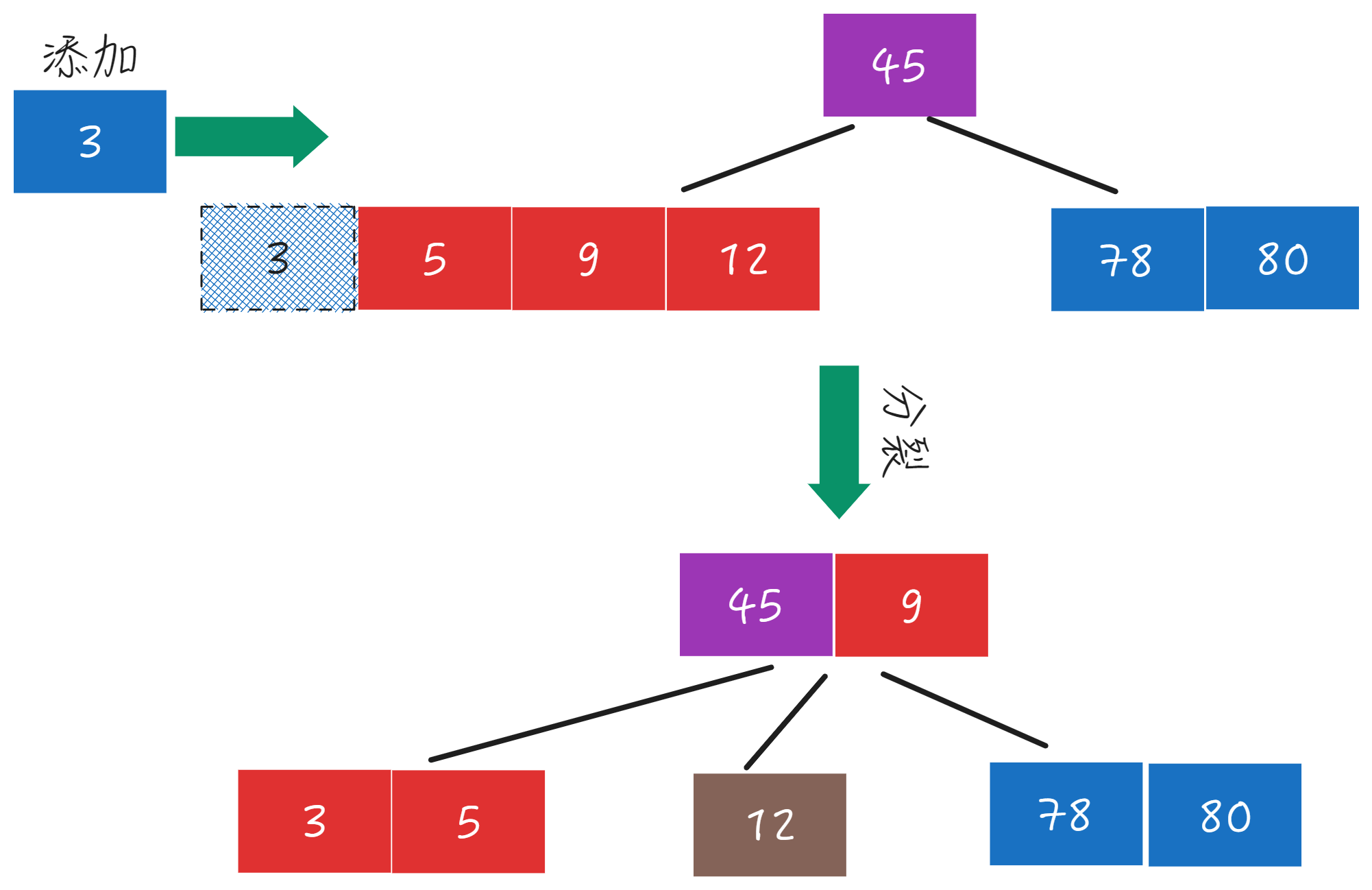
再次分裂
- 左侧分裂时检查父节点是否有空位,如果有把中间节点(9)放到父节点去
- 分裂出一下新节点存储中间节点的右侧数据 12
- 递归向上操作(如果父节点已满,继续向上操作直到父节点为根节点结束)
else {//如果parent不是根节点,且当前节点已满
//将中间值拷贝到parent节点中
insertBySort(parent, midVal);
curr.datas.remove(Integer.valueOf(midVal));
curr.size--;
parent.children.add(newNode); //将新
parent.children.sort((o1, o2) -> o1.datas.get(o1.size - 1) - o2.datas.get(0)); //对孩子节点安装正序排序
if (parent.size >= M) {
split(parent); //低估操作父节点
}
}
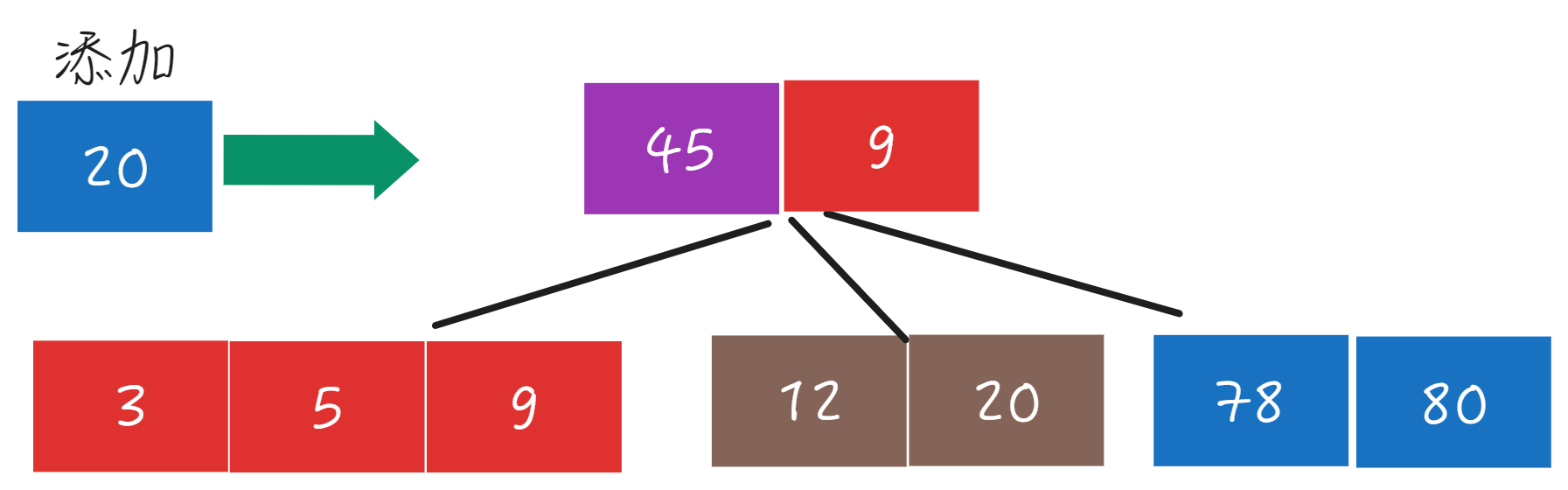
添加数据20
完整代码实现
B(B-)树节点
public class Node {
public List<Integer> datas; //记录数据
public List<Node> children; //子节点
public Node parent; //父节点
public int size; //节点内存储的值数量
public Node() {
datas = new ArrayList<>();
children = new ArrayList<>();
}
@Override
public String toString() {
return "Node{" +
"datas=" + datas +
", size=" + size +
'}';
}
}
B(B-)树的实现
辅助类NodeBind
辅助类NodeBind用来绑定在查询节点时,将节点和查询到B-树位置绑定。
如果节点没有查到,绑定当前节点,-1;如果查找到节点绑定当前节点,数据在节点中的位置。
/**
* 绑定数据在节点中位置类
*/
public class NodeBind {
private Node node; //当前节点
private int index; //当前节点中数据的位置
public Node getNode() {
return node;
}
public void setNode(Node node) {
this.node = node;
}
public int getIndex() {
return index;
}
public void setIndex(int index) {
this.index = index;
}
public NodeBind(Node node, int index) {
this.node = node;
this.index = index;
}
@Override
public String toString() {
return "Pair{" +
"node=" + node +
", index=" + index +
'}';
}
}
添加节点和分裂节点的实现
package com.ffyc.tree;
import com.ffyc.tree.node.Node;
import com.ffyc.tree.node.NodeBind;
import java.util.*;
public class BTree {
private Node root;
// M表示B-树的阶数
// 根节点的数据数: [1,M]之间
private final int M = 4; //4阶B-树
/**
* 添加节点数据
* @param data
*/
public void add(int data) {
if (root == null) {//如果根节点不存在
root = new Node();
root.datas.add(data);
root.size++;
return;
}
/*
从B-树中查找节点是否存在
*/
NodeBind findNode = search(data);
//数据已经在B树中,只更新不插入
if (findNode.getIndex() != -1) return;
/*
如果没有找到则插入节点
- 当前要插入的节点没有满
- 当前要插入的节点已满,需要分裂节点
*/
Node curr = findNode.getNode();
insertBySort(curr, data);
if (curr.size <= M - 1) { //如果当前节点的数据没有满,最大存储M-1数据
return;
} else { //当前节点已满
System.out.println("当前节点已满,准备分裂...");
split(curr);
}
}
/**
* B树的节点进行分裂
* @param curr 当前要分裂的节点
*/
public void split(Node curr) {
int mid = curr.size / 2; //找到中间节点
int midVal = curr.datas.get(mid);
Node parent = curr.parent;
/*
* 创建新节点,用来存储分裂的右侧节点
*/
Node newNode = new Node();
//newNode.datas = curr.datas.subList(mid + 1, curr.size);
for (int i = mid + 1; i < curr.size; i++) {
newNode.datas.add(curr.datas.get(i));
newNode.size++;
curr.datas.remove(i);
i--;
curr.size--;
}
/*
* 判断当前节点是否为根节点
*/
if (parent == null) {//父节点为空,当前节点为根节点
root = new Node();//产生一个新的父节点
root.datas.add(midVal); //拷贝当前节点的中间值到父节点中
curr.datas.remove(Integer.valueOf(midVal)); //从当前对象中移除已经添加到root上的数据
curr.size--;
root.size++; //父节点长度更新
root.children.add(curr); //父节点的孩子节点连接子节点
curr.parent = root; //当前节点的父节点变成新的父节点
root.children.add(newNode); //添加右侧的子节点到父节点的孩子节点中
newNode.parent = root; //右接点的父节点连接新父节点
return;
} else {//如果parent不是根节点,且当前节点已满
//将中间值拷贝到parent节点中
insertBySort(parent, midVal);
curr.datas.remove(Integer.valueOf(midVal));
curr.size--;
parent.children.add(newNode); //将新
parent.children.sort((o1, o2) -> o1.datas.get(o1.size - 1) - o2.datas.get(0));
if (parent.size >= M) {
split(parent);
}
}
}
/**
* 在节点中按顺序插入数据
* @param node
* @param data
*/
private void insertBySort(Node node, int data) {
int index = node.size;
for (int i = 0; i < node.datas.size(); i++) {
if (data < node.datas.get(i)) {
index = i;
break;
}
}
node.datas.add(index, data);
node.size++;
}
/**
* 查询data在B树的节点位置
*
* @param data
* @return
*/
public NodeBind search(int data) {
Node curr = root; //记录根节点,从根节点开始遍历
Node parent = curr.parent; //记录父节点
while (curr != null) { //从root遍历所有节点
int rowIndex = 0; // 每个节点中数据的存储位置索引
while (rowIndex < curr.size) { //扫描节点中所有数据
List<Integer> datas = curr.datas;
int index = datas.indexOf(data); //判断节点中的数据汇总是否包含要查找的数据
if (index != -1) { //数据存在,返回终止查找
return new NodeBind(curr, index);
} else if (data > datas.get(rowIndex)) { //数据大于节点中的数据,继续查找下一个数据
rowIndex++;
} else {//找到比节点中数据小的位置跳出循环,表示查找完毕没有找到
break;
}
}
parent = curr;
try {
curr = curr.children.get(rowIndex);
} catch (IndexOutOfBoundsException e) {
curr = null;
}
}
return new NodeBind(parent, -1);
}
public void print() {
Queue<Node> queue = new LinkedList<>();
queue.add(root);
while (!queue.isEmpty()) { //从root遍历所有节点
Node curr = queue.poll();
for (int i = 0; i < curr.size; i++) {
System.out.print(curr.datas.get(i) + "\t");
}
List<Node> children = curr.children;
for (Node node : children) {
queue.offer(node);
}
}
}
public Node getRoot() {
return this.root;
}
/**
* 测试代码
*/
public static void main(String[] args) {
BTree bTree = new BTree();
bTree.add(12);
bTree.add(45);
bTree.add(9);
bTree.add(78);
bTree.add(80);
bTree.add(5);
bTree.add(3);
bTree.add(79);
bTree.add(20);
bTree.add(1);
bTree.print();
}
}
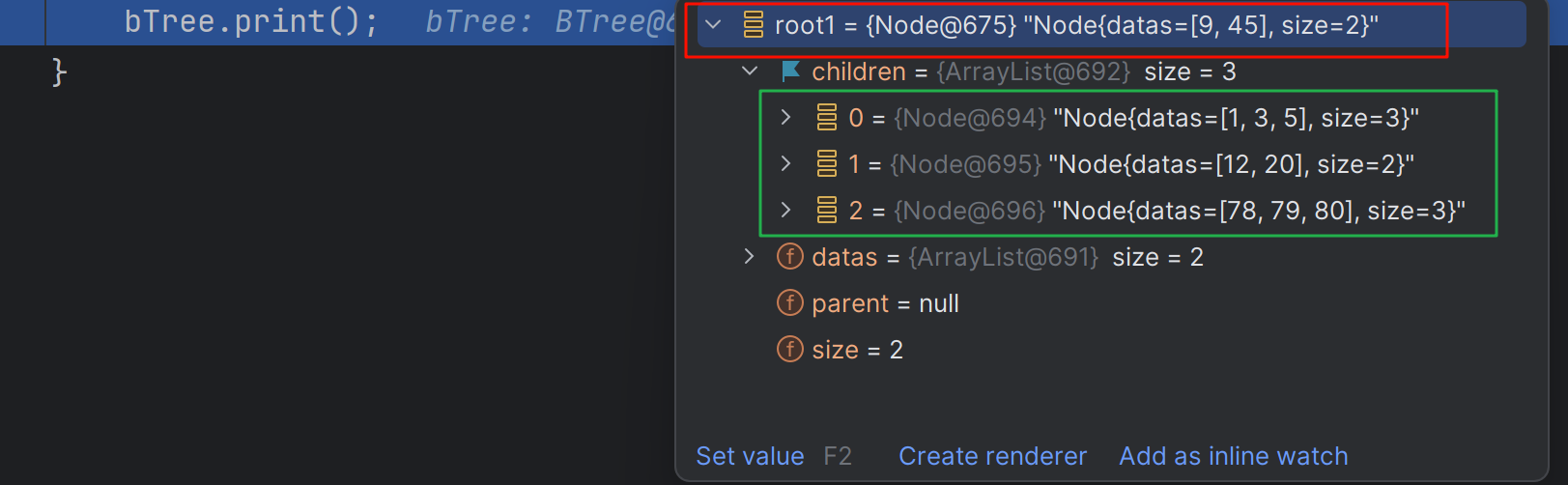
运行结果



![[数据集][目标检测]棉花叶子害虫检测数据集VOC+YOLO格式595张1类别](https://img-blog.csdnimg.cn/direct/02b44bb1e8cf4b6bb2cf8c5dd8f400c7.png)