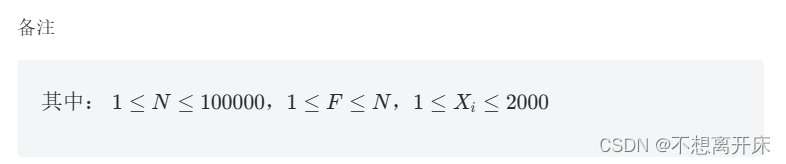状态压缩DP

定义

状态压缩DP是一种利用二进制数来表示状态的动态规划算法。它通过将状态压缩成一个整数，从而减少状态数量，提高算法效率。

运用情况

状态压缩DP通常用于解决具有状态转移和最优解性质的问题，例如组合优化、图论、游戏等问题。它的基本思想是将问题的状态表示为一个二进制数，其中每一位表示一个元素或一个状态。通过对二进制数的位运算，可以方便地进行状态转移和最优解的计算。

注意事项

1. 状态表示的合理性：确保状态表示能够准确地反映问题的特征和约束条件。
2. 状态转移的正确性：仔细设计状态转移方程，确保状态转移的正确性和有效性。
3. 边界情况的处理：考虑边界情况，如初始状态、终止状态等，进行特殊处理。
4. 空间复杂度的控制：由于状态数量可能很大，需要注意控制空间复杂度，避免内存溢出。
5. 位运算的优化：合理使用位运算，提高算法的效率。

解题思路

1. 状态表示：将问题的状态用二进制数表示，每个二进制位表示一个元素或状态。
2. 状态转移：根据问题的规则，设计状态转移方程，通过位运算实现状态的转移。
3. 初始化：确定初始状态，并进行相应的初始化操作。
4. 计算最优解：通过递推或迭代的方式，计算每个状态的最优解。
5. 输出结果：根据问题的要求，输出最终的最优解。

如何处理状态的溢出和下溢

• 状态压缩：使用二进制数来表示状态，通过位运算来进行状态转移和计算。这种方法可以大大减少状态的数量，提高算法的效率。
• 判断状态：在进行状态转移和计算时，需要判断当前状态是否合法。如果当前状态不合法，则需要进行特殊处理，例如忽略该状态或者将其标记为已访问。
• 初始化状态：在进行状态转移和计算时，需要对状态进行初始化。如果状态的初始值设置不合理，则可能会导致状态的溢出或下溢。
• 边界情况处理：在进行状态转移和计算时，需要考虑边界情况。如果边界情况处理不当，则可能会导致状态的溢出或下溢。

AcWing 291. 蒙德里安的梦想 

题目描述

291. 蒙德里安的梦想 - AcWing题库

运行代码

#include <iostream>
#include <cstring>
#include <vector>
using namespace std;
typedef long long LL;
const int N = 12, M = 1 << N;
int n, m;
LL f[N][M];
bool st[M];
vector<int> state[M];
int main()
{
    while(cin >> n >> m, n || m)
    {
        for(int i = 0; i < 1 << n; i++)
        {
            int ans = 0;
            bool is = true;
            for(int j = 0; j < n; j++)
            {
                if(i >> j & 1)
                {
                    if(ans & 1){ is = false; break;}
                    ans = 0;
                }
                else ans ++;
            }
            if(ans & 1) is = false;
            st[i] = is;
        }
        for(int i = 0; i < 1 << n; i++)
        {
            state[i].clear();
            for(int j = 0; j < 1 << n; j++)
                if((i & j) == 0 && st[i | j])
                    state[i].push_back(j);
        }
        memset(f, 0, sizeof f);
        f[0][0] = 1;
        for(int i = 1; i <= m; i++)
            for(int j = 0; j < 1 << n; j++)
                for(auto k : state[j])
                    f[i][j] += f[i - 1][k];
        cout << f[m][0] << endl;
    }
    return 0;
}

代码思路

1. 输入处理：首先，程序通过 cin >> n >> m 获取两个整数，其中 n 表示问题规模（通常是与二进制位数相关），m 是一个操作次数或阶段数。当 n 或 m 不为零时，继续执行。
2. 初始化状态：接下来，程序遍历所有 1 << n（即 2^n2n）种二进制状态（用整数表示），检查每个状态是否满足特定条件。这里的条件是：对于一个状态（二进制数），如果从左到右连续的0后面紧接着是1，则认为该状态无效（标记为 false，存储在数组 st[] 中），否则为有效（标记为 true）。这是通过累计0的个数并在遇到1时检查累计值的奇偶性来判断的。
3. 构建状态转移图：然后，程序构建一个“状态转移图”。对于每一个状态 i，找到所有与 i 按位或 (|) 后仍能保持有效的状态 j，并将这些状态添加到 state[i] 这个向量中。这一步实际上是为动态规划准备状态转移的基础，确保从一个有效状态通过某个操作可以转移到另一个有效状态。
4. 动态规划计算：初始化动态规划数组 f[][]，其中 f[i][j] 表示进行了 i 次操作后到达状态 j 的方案数。初始时，只有一种方法不进行任何操作到达初始状态（全0状态），即 f[0][0] = 1。
5. 遍历 m 次操作，对于每一次操作，以及当前可达的所有状态 j，考虑从所有能转移到 j 的前驱状态 k（存储在 state[j] 中）经过一次操作到达 j 的方案数，并累加到 f[i][j] 上。
6. 输出结果：最后，输出进行了 m 次操作后到达初始状态（全0状态）的方案数，即 f[m][0]。
7. 总结：这段代码的核心思想是使用动态规划和位操作来解决一个组合计数问题，特别是在有限状态空间内寻找满足特定转移规则的路径数量。通过构建状态转移关系并迭代计算，高效地得到了问题的解。

改进思路

1. 减少状态空间大小：如果题目条件允许，可以尝试减少需要枚举的状态数量。不过，从当前代码逻辑看，似乎已经利用了问题的特性（通过位运算处理状态转移），直接减小状态空间较为困难。

2. 内存优化：由于 f[][] 和 st[] 数组的大小与 n 直接相关，且随着 n 增大非常快，可以考虑使用滚动数组或者空间压缩技巧来减少内存使用。对于 f[][]，实际上每一阶段只需要上一阶段的状态，因此可以使用一维数组滚动更新。

3. 避免重复计算：当前代码在计算状态转移时，对于每个状态 j，都会遍历其所有可能的前驱状态并累加方案数。如果存在大量重复计算的情况，可以考虑使用记忆化搜索或更高效的数据结构来存储中间结果。

4. 代码可读性和维护性：增加注释，对关键变量和步骤进行解释，使代码更易于理解和维护。