一、定义
树(Tree)是n(n>=0)个结点的有限集。当n=0时成为空树,在任意一棵非空树中:
1、有且仅有一个特定的称为根(Root)的结点;
2、当n>1时,其余结点可分为m(m>日)个互不相交的有限集T1、T2、...、 Tm,其中每一个集合本身又是一棵树,并且称为根的子树(SubTree)。
需要注意的是:
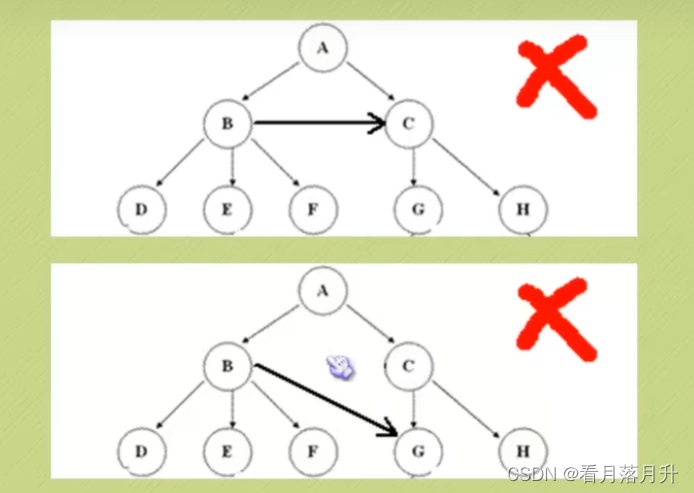
1、n>6时,根结点是唯一的,坚决不可能存在多个根结点。
2、m>0时,子树的个数是没有限制的,但它们互相是一定不会相交的。
二、节点分类
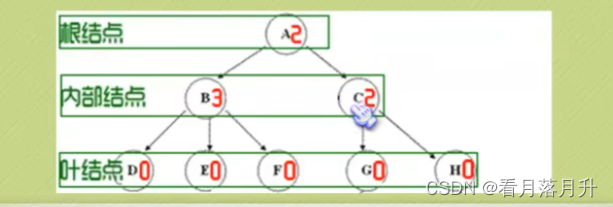
刚才所有图片中,每一个圈圈我们就称为树的一个结点。结点拥有的子树数称为结点的度-
(Degree),树的度取树内各结点的度的最大值。
1、度为0的结点称为叶结点(Leaf)或终端结点;
2、度不为0的结点称为分支结点或非终端结点,除根结点外,分支结点也称为内部结点。
三、结点间的关系
结点的子树的根称为结点的孩子(Child),相应的,该结点称为孩子的双亲(Parent),同一双亲的孩子之间互称为兄弟(Sibling)。
结点的祖先是从根到该结点所经分支上的所有结点。
四、节点的层次
- 结点的层次(Level)从根开始定一起,根为第一层,根的孩子为第二层。
- 其双亲在同一层的结点互为堂兄弟。
- 树中结点的最大层次称为树的深度(Depth)或高度。
五、其他概念
- 如果将树中结点的各子树看成从左至右是有次序的,不能互换的,则称该树为有序树,否则称为无序树。
- 森林(Forest)是 m(m>=0)棵互不相交的树的集合。对树中每个结点而言,其子树的集合即为森林。
六、树的存储结构
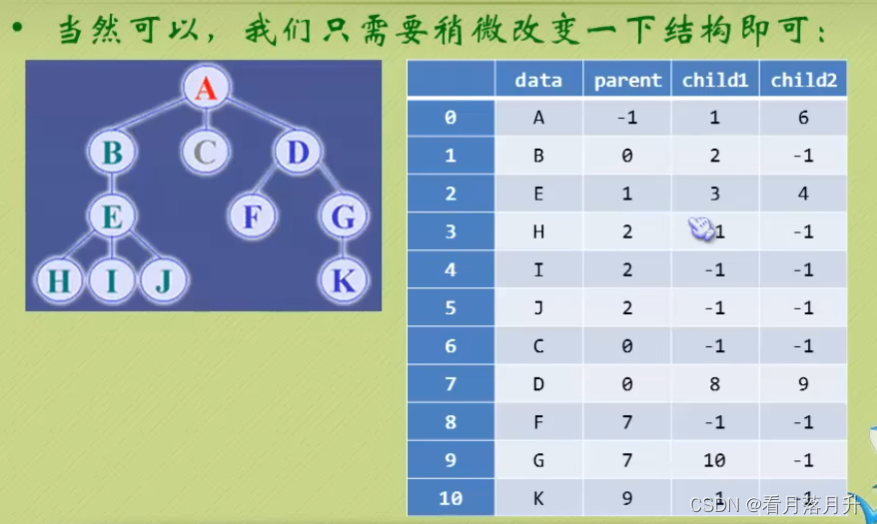
1、双亲表示法
双亲表示法,言外之意就是以双亲作为索引的关键词的一种存储方式。
我们假设以一组连续空间存储树的结点,同时在每个结点中,附设一个指示其双亲结点在数组中位置的元素。
也就是说,每个结点除了知道自己是谁之外,还知道它的粑粑妈妈在哪里。
定义一个结构体
#define MAXSIZE 100
typedef struct PTNode {
int data; //结点数据
int parent; //双亲位置
}PTNode;
typedef struct {
PTNode node[MAXSIZE];
int r; //根的位置
int n; //节点数目
}PTree;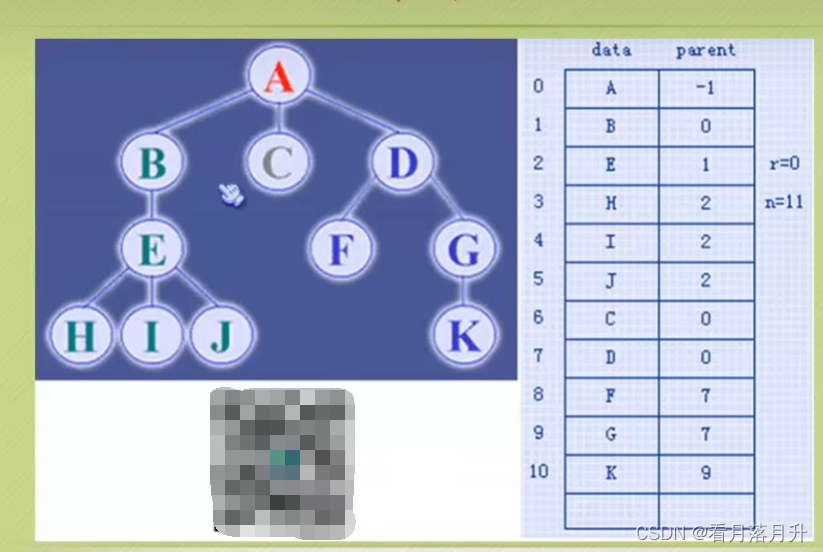
这样的存储结构,我们可以根据某结点的parent指针找到它的双亲结点,所用的时间复杂度是0(1),索引到parent的值为-1时,表示找到了树结点的根。
可是,如果我们要知道某结点的孩子是什么?那么不好意思,请遍历整个树结构
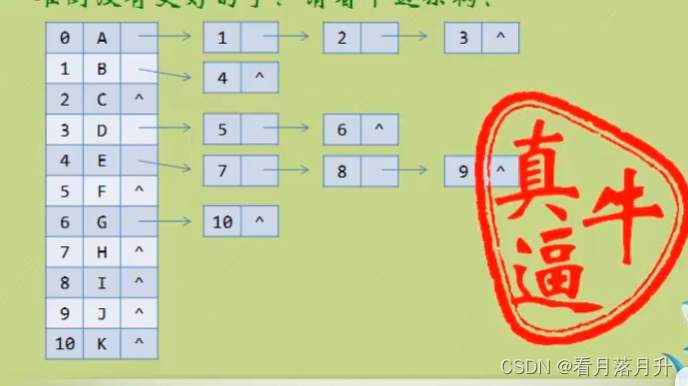
2、孩子表示法
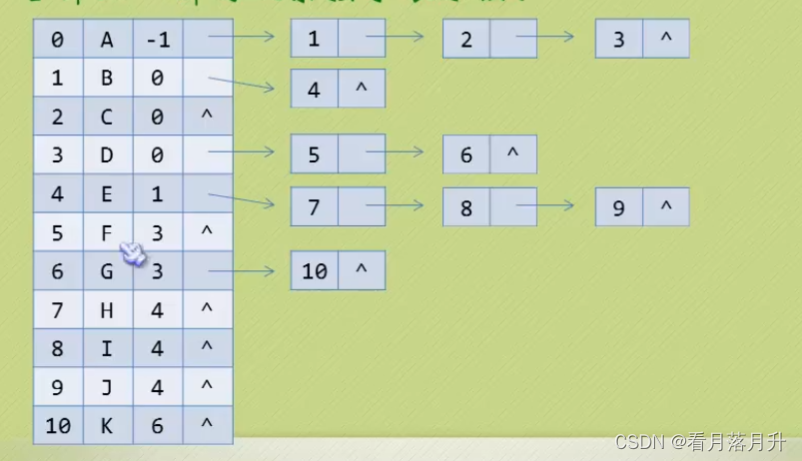
3、双亲孩子表示法
//孩子节点
typedef struct CTNode {
int child; //孩子结点的下标
struct CTNode* next; //指向下一个孩子结点的指针
}*ChildPtr;
//表头结构
typedef struct {
int data; //存放在树中的节点数据
int paraent; //存放双亲的下标
ChildPtr friendchild; //指向第一个孩子的指针
}CTBox;
//树结构
typedef struct {
CTBox node[MAXSIZE];
int r, n;
}CTTree;七、二叉树
1、定义
二叉树(Binary Tree)是n(n>=0)个结点的有限集合,该集合或者为空集(空二叉树),或者由一个根结点和两棵互不相交的、分别称为根结点的左子树和右子树的二叉树组成。
注意:
每个结点最多有两棵子树,所以二叉树中不存在度大于2的结点。(注意:不是都需要两棵子树,而是最多可以是两棵,没有子树或者有一棵子树也都是可以的。)
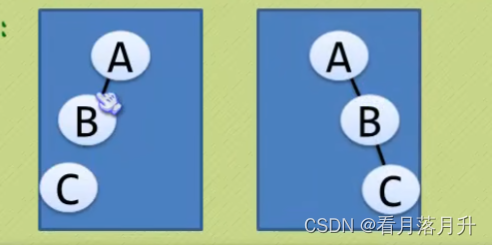
左子树和右子树是有顺序的,次序不能颠倒。
即使树中某结点只有一棵子树,也要区分它是左子树还是右子树,下面是完全不同的二叉树:
2、五种基本形态
(1)空二叉树
(2)只有一个根结点
(3)根结点只有左子树
(4)根结点只有右子树
(5)根结点既有左子树又有右子树
3、特殊二叉树
(1)斜树
斜树是一定要斜的,但斜也要斜寻有范儿
(2)满二叉树
在一棵二叉树中,如果所有分支结点都存在左子树和右子树,并且所有叶子都在同一层上,这样的二叉树称为满二叉树。
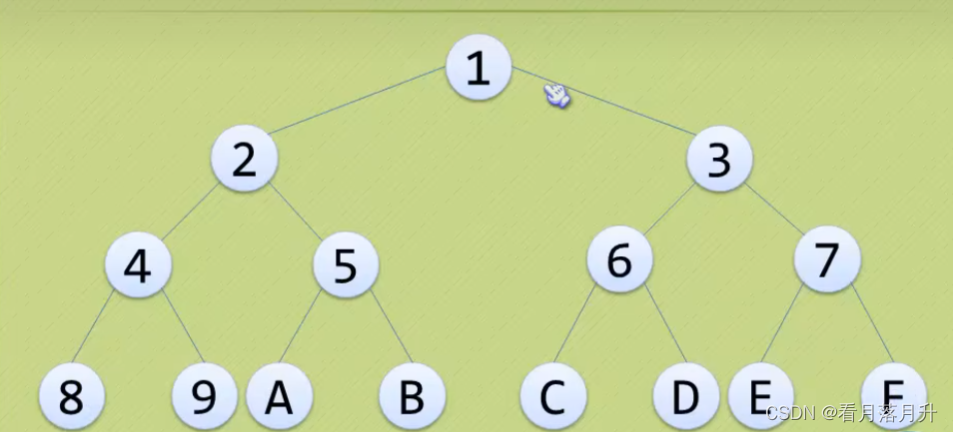
特点:
- 叶子只能出现在最下一层。
- 非叶子结点的度一定是2。
- 在同样深度的二叉树中,满二又树的结点个数一定最多,同时叶子也是最多。
(3)完全二叉树
对一棵具有n个结点的二叉树按层序编号,如果编号为i(1<=i<=n)的结点与同样深度的满二叉树中编号为i的结点位置完全相同,则这棵二叉树称为完全二叉树。
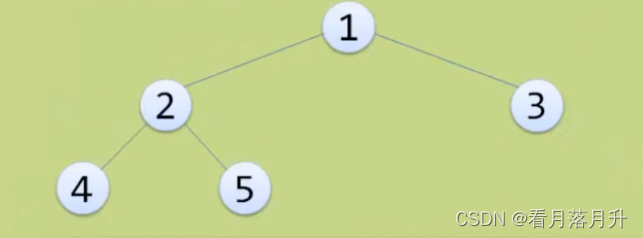
这个也是满二叉树
特点:
- 叶子结点只能出现在最下两层。
- 最下层的叶子一定集中在左部连续位置。
- 倒数第二层,若有叶子结点,一定都在右部连续位置。
- 如果结点度为1,则该结点只有左孩子。
- 同样结点树的二叉树,完全二叉树的深度最小。
注意:满二叉树一定是完全二叉树,但完全二叉树不一定是满二叉树。
重点:
二叉树的性质一:在二叉树的第i层上至多2^(i-1)个结点(i>=1)
二叉树的性质二:深度为k的二叉树至多有2^k-1个结点(k>=1)
二叉树的性质三:对任何一棵二叉树T,如果其终端结点数为n0,度为2的结点数为n2,则n0=n2+1

(打岔一下,在纸面上写写画画很重要的!!!)
二叉树的性质四:具有n个结点的完全二叉树的深度为 ,向下取整
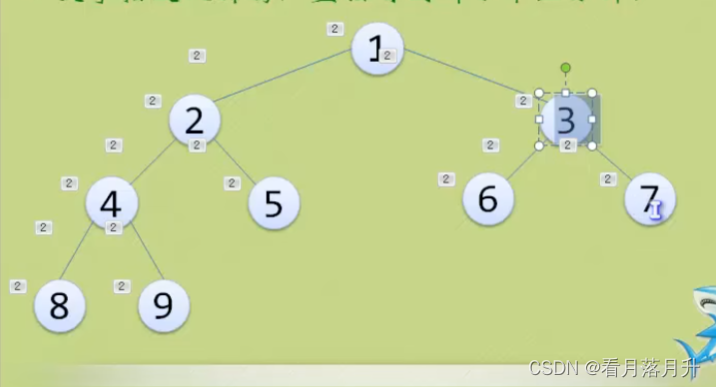
二叉树的性质五:如果对一棵有n个结点的完全二叉树(其深度为[log2n]+1)的结点按层序编号,对任一结点i(1<=i<=n)有以下性质:
- 如果i =1,则结点i是二叉树的根,无双亲;如果i >1,则其双亲是结点
- 如果2i > n,则结点i无左孩子(结点i为叶子结点);否则其左孩子是结点2i
- 如果2i+1 >n,则结点i无右孩子;否则其右孩子是结点2i+1
4、存储结构
(1)顺序存储
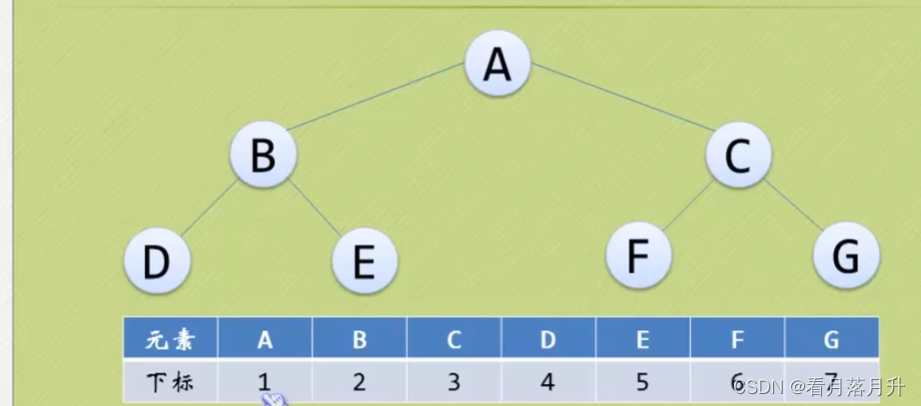
对于完全二叉树是十分方便的,但是一般二叉树就不行了,空间会造成极大的浪费
(2)链式存储!!!!
结点结构

代码
typedef struct BiNode {
int data;
struct BiTNode* lchild, * rchild;
}BiTNode,*BiTree;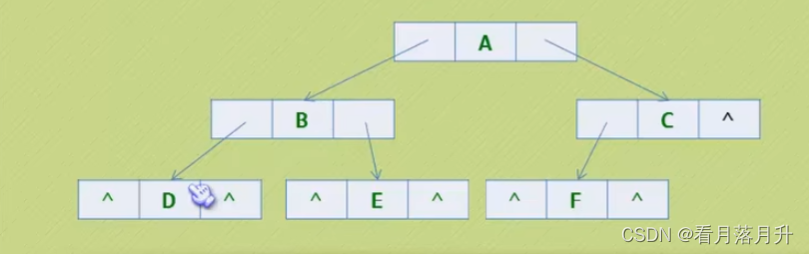
5、二叉树的遍历
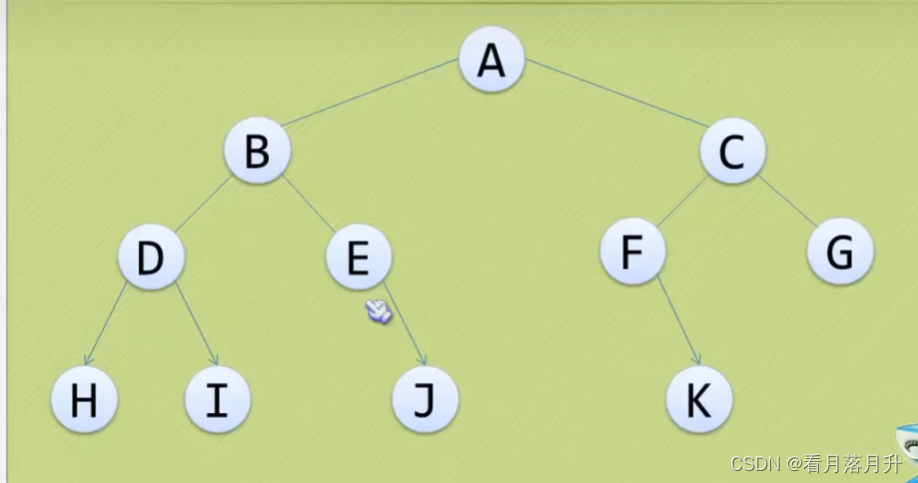
(1)先序遍历
根——>左子树——>右子树
ABDHIEJCFKG
(2)中序遍历
左子树——>根——>右子树
HDIBEGAFKCG
(3)后序遍历
左子树——>右子树——>根
HIDJEBKFGCA
(4)层序遍历
ABCDEFGHIJK
八、二叉树的建立和遍历算法
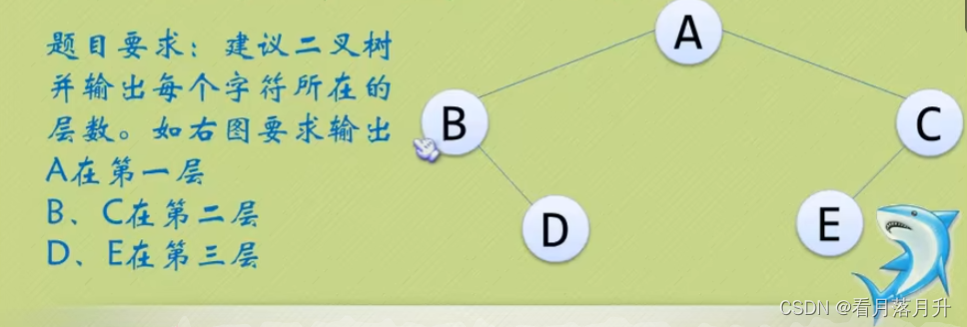
代码(包括递归和非递归遍历):
#define _CRT_SECURE_NO_WARNINGS 1;
#include <stdio.h>
#include <stdlib.h>
typedef struct TreeNode {
char val;
struct TreeNode* left;
struct TreeNode* right;
} TreeNode;
TreeNode* createTree(char** str) {
//*str就是 char数组的指针
if (**str == '#') {
(*str)++; //指针偏移
return NULL;
}
TreeNode* node = (TreeNode*)malloc(sizeof(TreeNode));
node->val = **str;
(*str)++;
//这里递归实现,从根节点开始往左子树里填
node->left = createTree(str);
node->right = createTree(str);
return node;
}
// 递归遍历
void preOrderRecursive(TreeNode* root) {
if (root == NULL) return;
printf("%c ", root->val);
preOrderRecursive(root->left);
preOrderRecursive(root->right);
}
void inOrderRecursive(TreeNode* root) {
if (root == NULL) return;
inOrderRecursive(root->left);
printf("%c ", root->val);
inOrderRecursive(root->right);
}
void postOrderRecursive(TreeNode* root) {
if (root == NULL) return;
postOrderRecursive(root->left);
postOrderRecursive(root->right);
printf("%c ", root->val);
}
// 非递归遍历使用栈来辅助
#define MAX_SIZE 100
typedef struct {
TreeNode* data[MAX_SIZE];
int top;
} Stack;
void initStack(Stack* s) {
s->top = -1;
}
int isEmpty(Stack* s) {
return s->top == -1;
}
int isFull(Stack* s) {
return s->top == MAX_SIZE - 1;
}
void push(Stack* s, TreeNode* node) {
if (isFull(s)) return;
s->data[++(s->top)] = node;
}
TreeNode* pop(Stack* s) {
if (isEmpty(s)) return NULL;
return s->data[(s->top)--];
}
void preOrderNonRecursive(TreeNode* root) {
if (root == NULL) return;
Stack s;
initStack(&s);
push(&s, root);
while (!isEmpty(&s)) {
TreeNode* node = pop(&s);
printf("%c ", node->val);
if (node->right) push(&s, node->right);
if (node->left) push(&s, node->left);
}
}
void inOrderNonRecursive(TreeNode* root) {
Stack s;
initStack(&s);
TreeNode* cur = root;
while (cur || !isEmpty(&s)) {
while (cur) {
push(&s, cur);
cur = cur->left;
}
cur = pop(&s);
printf("%c ", cur->val);
cur = cur->right;
}
}
void postOrderNonRecursive(TreeNode* root) {
if (root == NULL) return;
Stack s1, s2;
initStack(&s1);
initStack(&s2);
push(&s1, root);
while (!isEmpty(&s1)) {
TreeNode* node = pop(&s1);
push(&s2, node);
if (node->left) push(&s1, node->left);
if (node->right) push(&s1, node->right);
}
while (!isEmpty(&s2)) {
TreeNode* node = pop(&s2);
printf("%c ", node->val);
}
}
int main() {
char input[101];
scanf("%s", input);
char* str = input;
TreeNode* root = createTree(&str);
// 递归遍历
preOrderRecursive(root);
printf("\n");
inOrderRecursive(root);
printf("\n");
postOrderRecursive(root);
printf("\n");
// 非递归遍历
preOrderNonRecursive(root);
printf("\n");
inOrderNonRecursive(root);
printf("\n");
postOrderNonRecursive(root);
printf("\n");
return 0;
}
这里的递归好理解,对于非递归
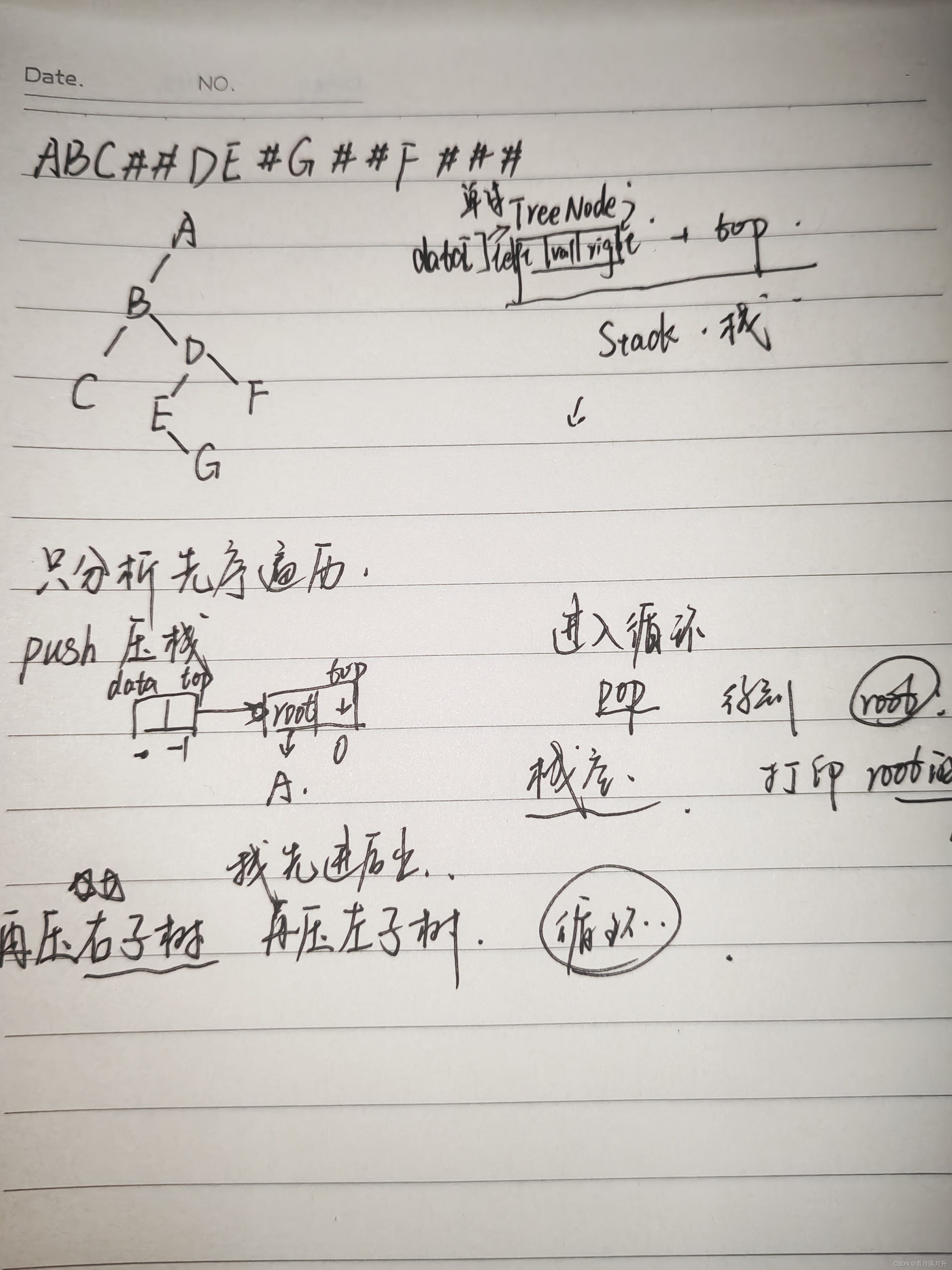
九、线索二叉树

结构体
//二叉树的二又线索存储表示
typedef struct BiThrNode{
TElemType data;
struct BiThrNode *lchild, *rchild;
int LTag, RTag;
}BiThrNode, *BiThrTree;用实线表示孩子节点,虚线表示前驱后继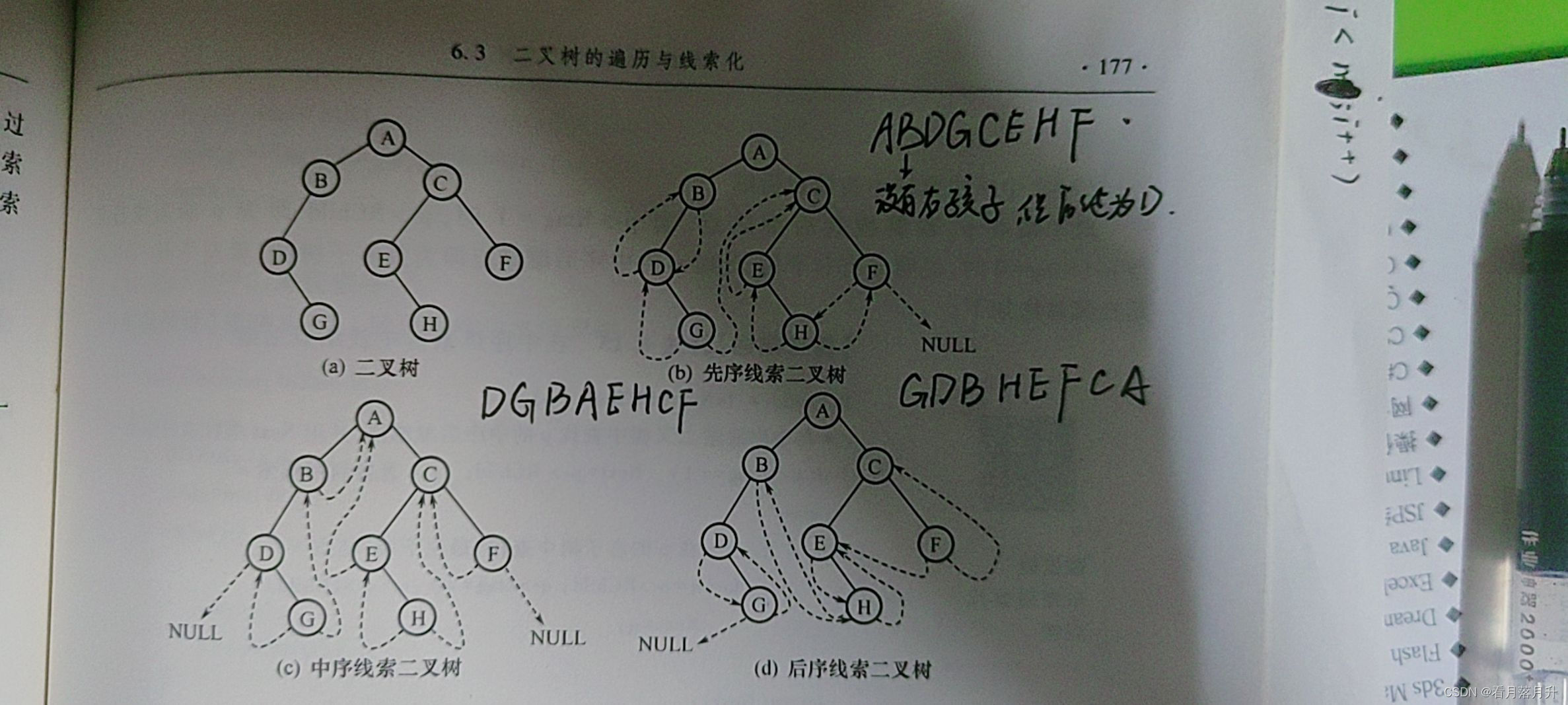
中序线索代码实现
结构体
typedef struct Thread {
struct Thread* left_node, * right_node;//左右指针
int data;//需要存放的数据
/*默认0代表左右孩子 1代表前驱或者后继*/
int left_type;//类型标志
int right_type;//类型标志
}Node;
Node* pre;//前驱结点的变量
Node* head;//头指针 指向某种遍历的第一个结点线索化
void inOrderThreadTree(Node* node)
{
//如果当前结点为NULL 直接返回
if (node == NULL) {
return;
}
//先处理左子树
inOrderThreadTree(node->left_node);
if (node->left_node == NULL)
{
//设置前驱结点
node->left_type = 1;
node->left_node = pre;
}
//如果结点的右子节点为NULL 处理前驱的右指针
if (pre !=NULL && pre->right_node == NULL)
{
//设置后继
pre->right_node = node;
pre->right_type = 1;
}
//每处理一个节点 当前结点是下一个节点的前驱
pre = node;
//最后处理右子树
inOrderThreadTree(node->right_node);
}遍历
void inOrderTraverse(Node* root)
{
//从根节点开始先找到最左边
if (root == NULL)
{
return;
}
Node* temp = root;
//先找到最左边结点 然后根据线索化直接向右遍历
while (temp != NULL && temp->left_type == 0)
{
temp = temp->left_node;
}
while (temp != NULL)
{
//输出
temp = temp->right_node;
}
}这里停一下,时间不多,前驱后继就不写了哈
十、树、森林继二叉树的相互转换
1、树转换为二叉树
树转换成相应的二叉树分两个步骤:
- 在树中所有的兄弟结点之间加一连线
- 对每个结点,除了保留与其长子的连线外,去掉该结点与其他孩子的连线
只有左子树
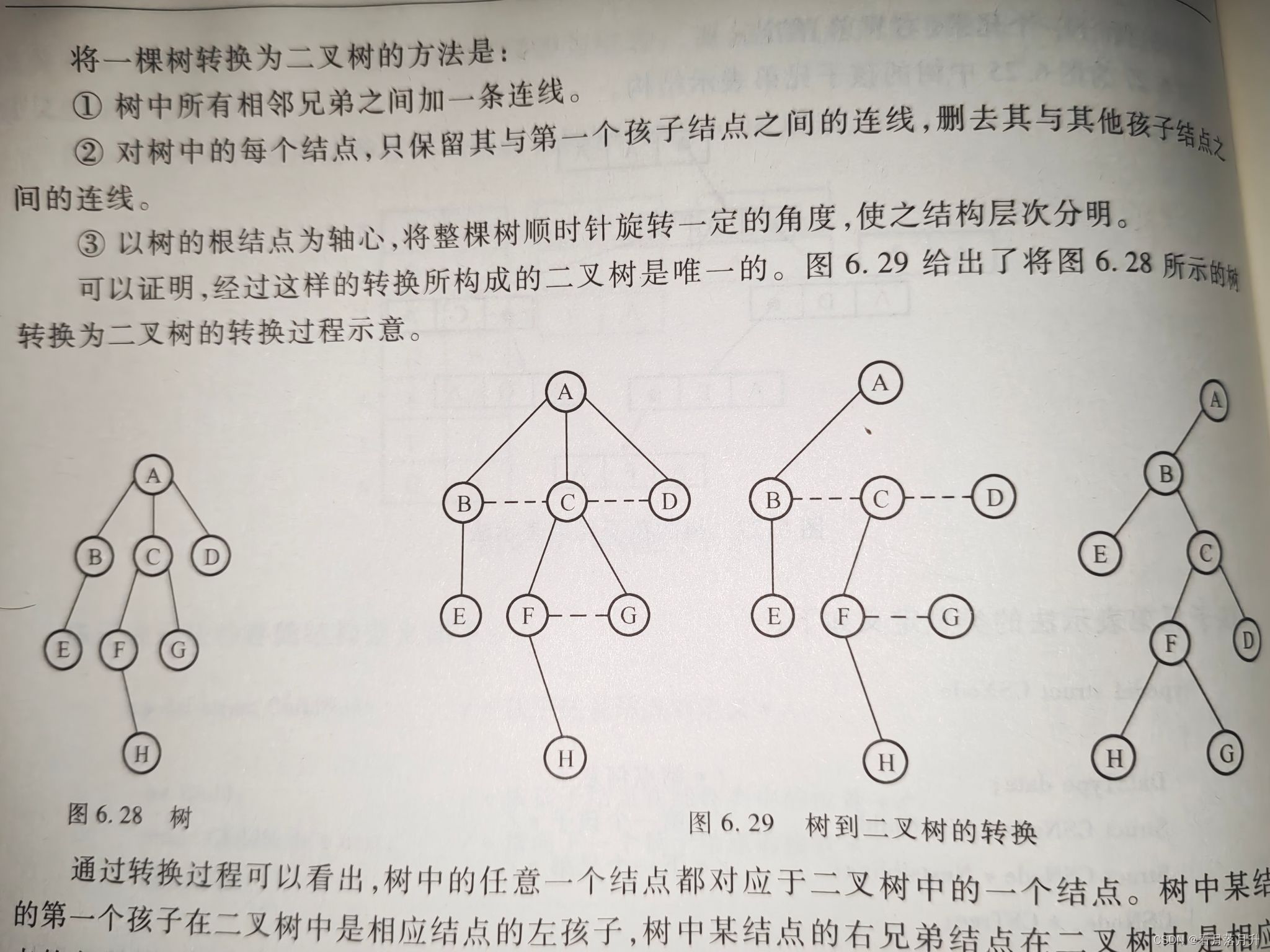
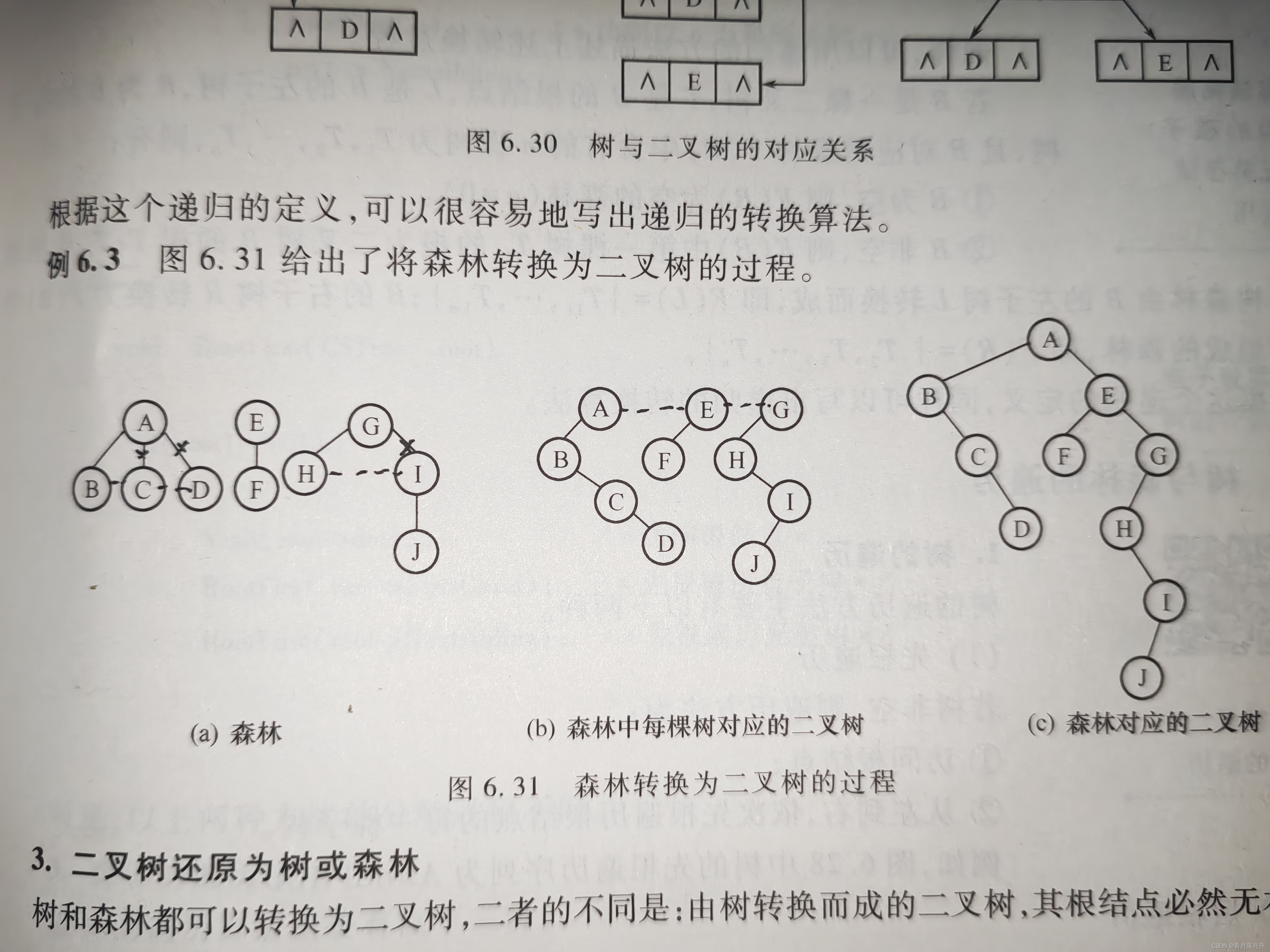
2、森林到二叉树的转换
森林转换为二叉树分两个步骤:
- 先将森林中的每棵树变为二叉树
- 再将各二叉树的根结点视为兄弟从左至右连在一起,就形成了一棵二叉树
3、二叉树到树、森林的转换
- 若结点x是其双亲y的左孩子,则把x的右孩子,右孩子的右孩子,…,都与y用连线连起来。
- 去掉所有双亲到右孩子之间的连线
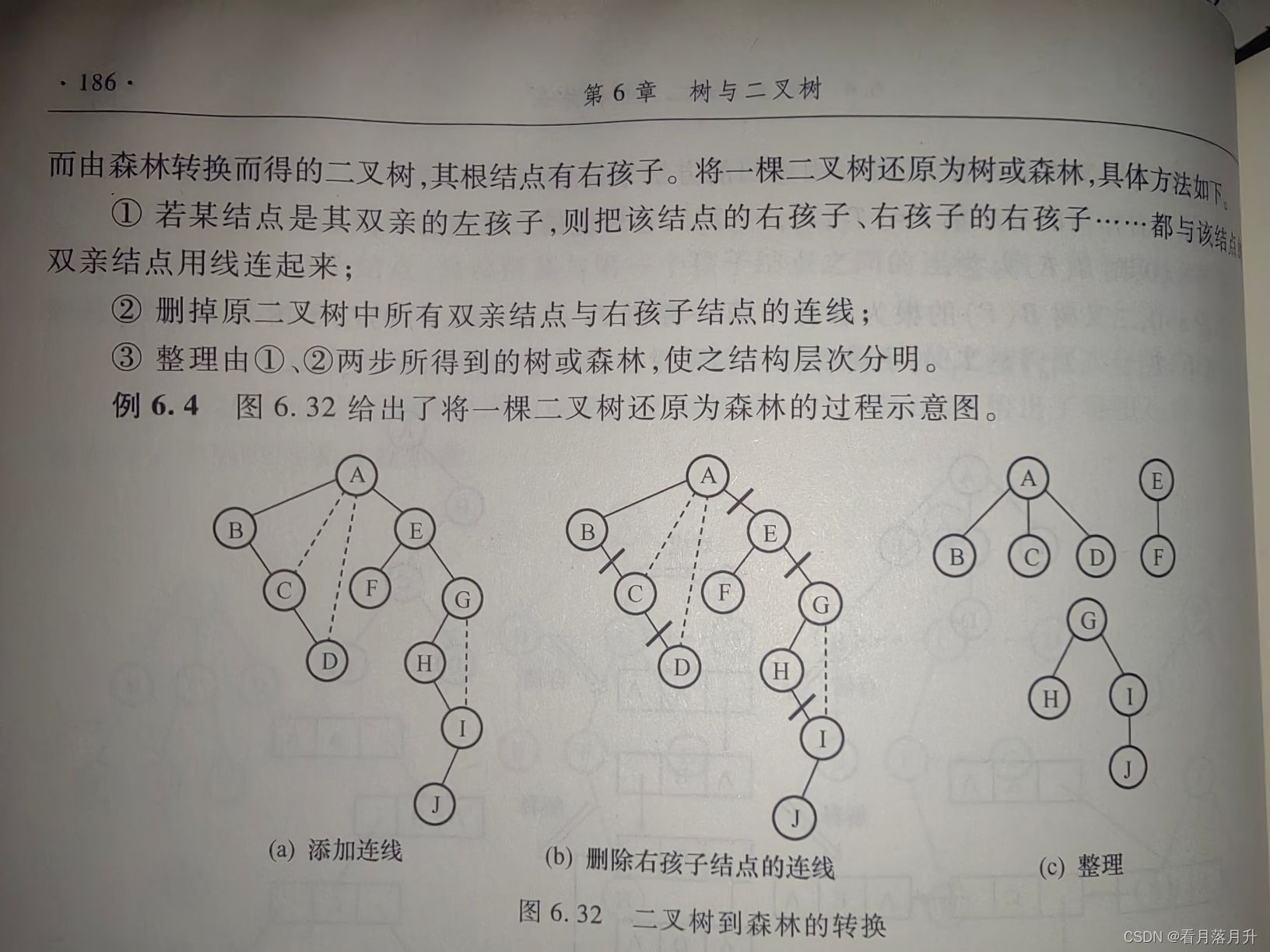
4、树与森林的遍历
树的遍历分为两种方式:一种是先根遍历,另一种是后根遍历。
- 先根遍历:先访问树的根结点,然后再依次先根遍历根的每棵子树。
- 后根遍历:先依次遍历每棵子树,然后再访问根结点。
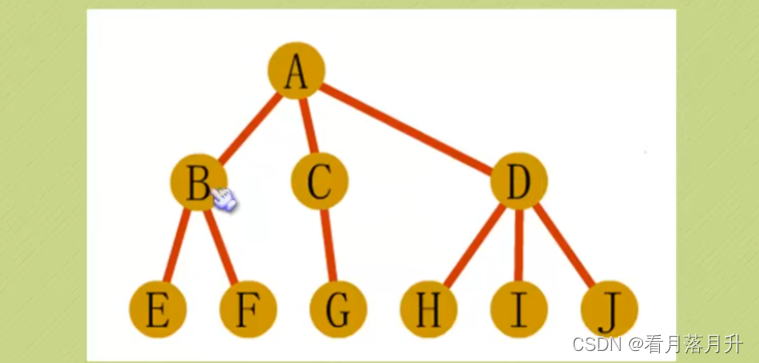
先根遍历:ABEFCGDHIJ
后根遍历:EFBGCHIJDA
森林的遍历也分为前序遍历和后序遍历,其实就是按照树的先根遍历和后根遍历依次访问森林的每一棵树。
我们的惊人发现:树、森林的前根(序)遍历和二叉树的前序遍历结果相同,树、森林的后根(序)遍历和二叉树的中序遍历结果相同!
十一、哈夫曼树
1、定义
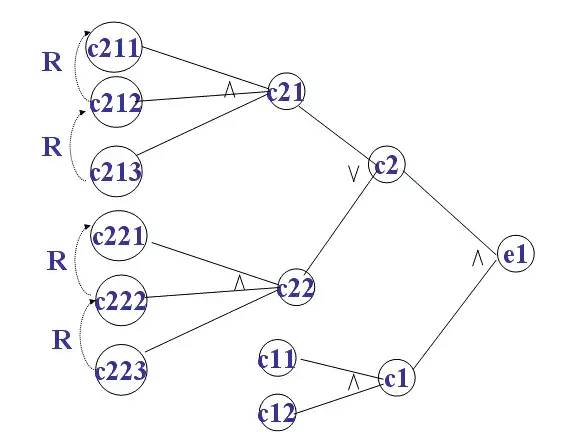
我们先把这两棵二叉树简化成叶子结点带权的二叉树(注:树结点间的连线相关的数叫做权,Weight) 。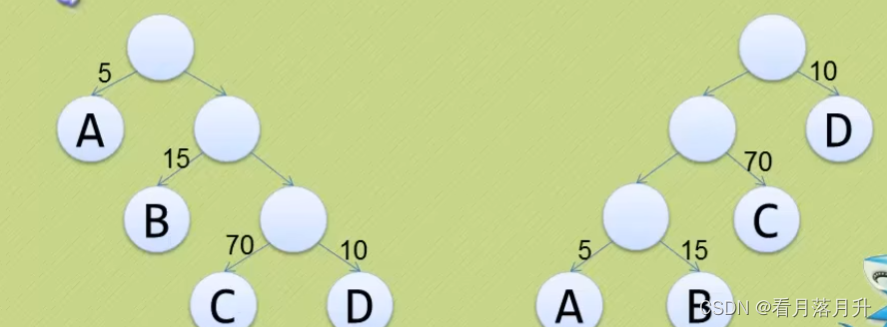
- 结点的路径长度:从根结点到该结点的路径上的连接数。 第一幅图C的就是3
- 树的路径长度:树中每个叶子结点的路径长度之和。 第一幅图为1+2+3+3 = 9
- 结点带权路径长度:结点的路径长度与结点权值的乘积。 第一幅图C的就是3*70=210
- 树的带权路径长度:-WPL(Weighted Path Length)是树中所有叶子结点的带权路径长度之和。第一幅图为1*5+2*15+3*70+3*10 = 275
WPL的值越小,说明构造出来的二叉树性能越优。
构造过程:
1、构造森林全是根; 2、选用两小造新树;
3、删除两小添新人 ;4、重复2、3剩单根。
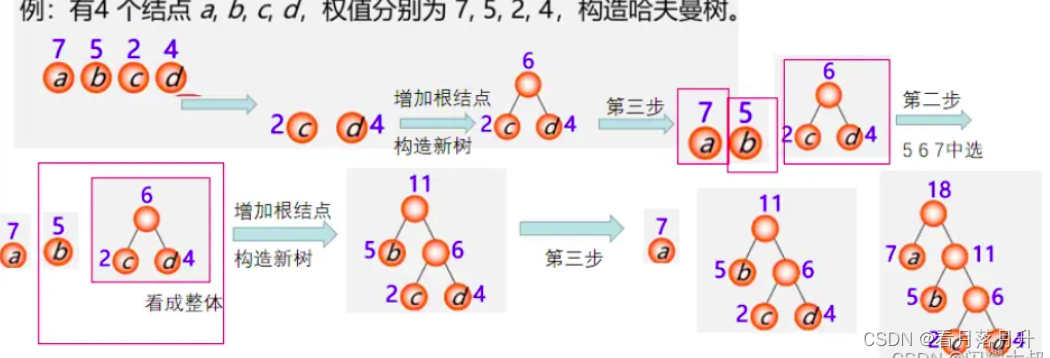
2、哈夫曼树的构建
结构体
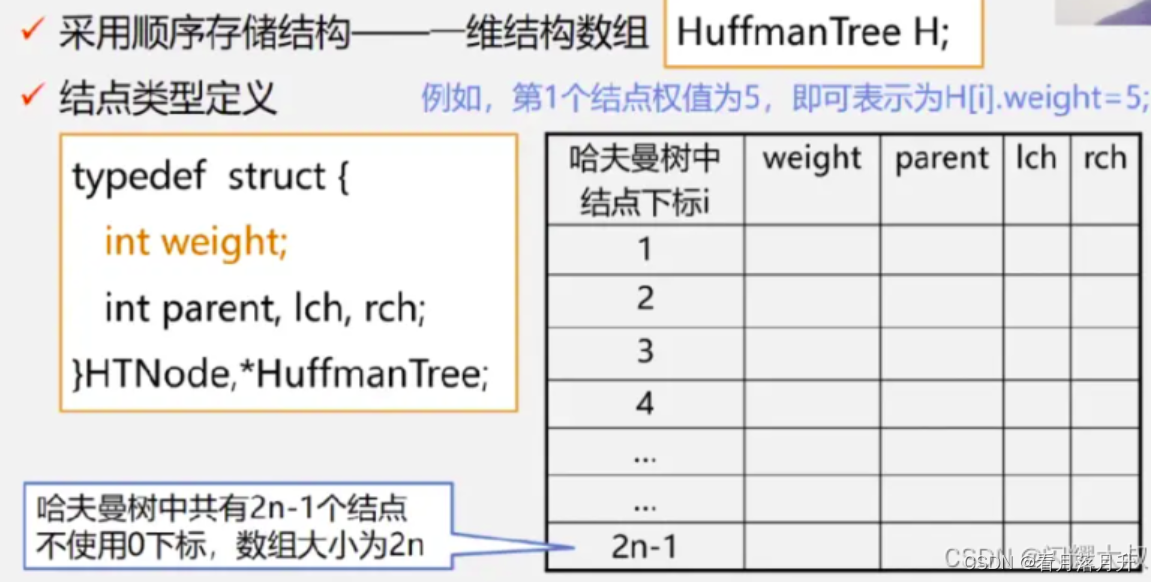
//哈夫曼树结点结构
typedef struct {
int weight;//结点权重
int parent, left, right;//父结点、左孩子、右孩子在数组中的位置下标
}HTNode, *HuffmanTree;构建
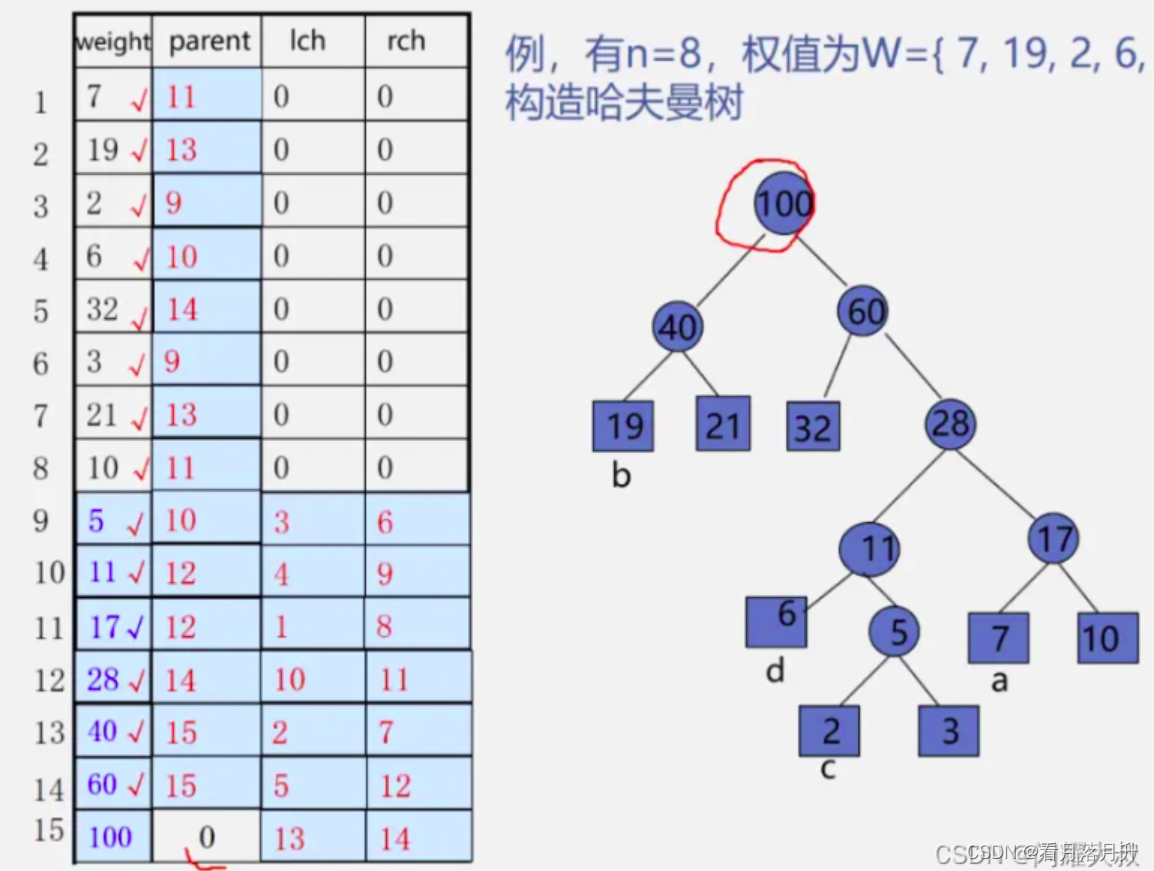
//HT为地址传递的存储哈夫曼树的数组,w为存储结点权重值的数组,n为结点个数
void CreateHuffmanTree(HuffmanTree *HT, int *w, int n)
{
if(n<=1) return; // 如果只有一个编码就相当于0
int m = 2*n-1; // 哈夫曼树总节点数,n就是叶子结点
*HT = (HuffmanTree) malloc((m+1) * sizeof(HTNode)); // 0号位置不用
HuffmanTree p = *HT;
// 初始化哈夫曼树中的所有结点
for(int i = 1; i <= n; i++)
{
(p+i)->weight = *(w+i-1);
(p+i)->parent = 0;
(p+i)->left = 0;
(p+i)->right = 0;
}
//从树组的下标 n+1 开始初始化哈夫曼树中除叶子结点外的结点
for(int i = n+1; i <= m; i++)
{
(p+i)->weight = 0;
(p+i)->parent = 0;
(p+i)->left = 0;
(p+i)->right = 0;
}
//构建哈夫曼树
for(int i = n+1; i <= m; i++)
{
int s1, s2;
Select(*HT, i-1, &s1, &s2);
(*HT)[s1].parent = (*HT)[s2].parent = i;
(*HT)[i].left = s1;
(*HT)[i].right = s2;
(*HT)[i].weight = (*HT)[s1].weight + (*HT)[s2].weight;
}
}3、重难点:哈夫曼编码
1. 计算字符串中每个字符的频率
2. 按照字符出现的频率进行排序,组成一个队列 Q
3. 把这些字符作为叶子节点开始构建一棵哈夫曼树
4. 对字符进行编码

哈夫曼树和编码都不唯一!只有树的WPL(带权路径长度)才是唯一的!
代码实现:
#include <stdio.h>
#include <stdlib.h>
// 定义哈夫曼树节点结构
typedef struct HuffmanNode {
char data; // 字符
int freq; // 频率
struct HuffmanNode* left, * right; // 左右子节点
} HuffmanNode;
// 定义优先级队列结构
typedef struct PriorityQueue {
int size; // 队列当前大小
int capacity; // 队列容量
HuffmanNode** array; // 存储哈夫曼树节点的数组指针
} PriorityQueue;
// 创建哈夫曼树节点
HuffmanNode* createNode(char data, int freq) {
HuffmanNode* node = (HuffmanNode*)malloc(sizeof(HuffmanNode)); // 分配内存空间
node->data = data; // 设置节点字符
node->freq = freq; // 设置节点频率
node->left = node->right = NULL; // 初始化左右子节点为空
return node; // 返回节点指针
}
// 创建优先级队列
PriorityQueue* createPriorityQueue(int capacity) {
PriorityQueue* queue = (PriorityQueue*)malloc(sizeof(PriorityQueue)); // 分配内存空间
queue->size = 0; // 初始化队列大小为0
queue->capacity = capacity; // 设置队列容量
queue->array = (HuffmanNode**)malloc(queue->capacity * sizeof(HuffmanNode*)); // 分配内存空间
return queue; // 返回队列指针
}
// 交换两个节点
void swapNodes(HuffmanNode** a, HuffmanNode** b) {
HuffmanNode* temp = *a;
*a = *b;
*b = temp;
}
// 向下堆化
void minHeapify(PriorityQueue* queue, int idx) {
int smallest = idx;
int left = 2 * idx + 1; // 计算左子节点索引
int right = 2 * idx + 2; // 计算右子节点索引
// 找出三个节点中最小的节点
if (left < queue->size && queue->array[left]->freq < queue->array[smallest]->freq) {
smallest = left;
}
if (right < queue->size && queue->array[right]->freq < queue->array[smallest]->freq) {
smallest = right;
}
// 如果最小节点不是当前节点,交换节点并递归向下堆化
if (smallest != idx) {
swapNodes(&queue->array[idx], &queue->array[smallest]);
minHeapify(queue, smallest);
}
}
// 插入节点
void insertNode(PriorityQueue* queue, HuffmanNode* node) {
queue->size++; // 队列大小加1
int i = queue->size - 1; // 获取最后一个位置的索引
queue->array[i] = node; // 将节点插入最后一个位置
// 如果插入节点的频率小于父节点的频率,向上调整
while (i && queue->array[i]->freq < queue->array[(i - 1) / 2]->freq) {
swapNodes(&queue->array[i], &queue->array[(i - 1) / 2]);
i = (i - 1) / 2;
}
}
// 提取最小节点
HuffmanNode* extractMin(PriorityQueue* queue) {
if (queue->size == 0) return NULL; // 如果队列为空,返回空指针
HuffmanNode* root = queue->array[0]; // 获取根节点
queue->array[0] = queue->array[queue->size - 1]; // 将最后一个节点移到根节点位置
queue->size--; // 队列大小减1
minHeapify(queue, 0); // 向下堆化
return root; // 返回根节点
}
// 构建哈夫曼树
HuffmanNode* buildHuffmanTree(char data[], int freq[], int size) {
PriorityQueue* queue = createPriorityQueue(size); // 创建优先级队列
// 将字符和频率构建成哈夫曼树节点,并插入优先级队列中
for (int i = 0; i < size; i++) {
insertNode(queue, createNode(data[i], freq[i]));
}
// 从优先级队列中不断取出最小的两个节点,构建哈夫曼树,直到队列中只剩一个节点
while (queue->size != 1) {
HuffmanNode* left = extractMin(queue);
HuffmanNode* right = extractMin(queue);
// 创建新节点作为父节点,频率为左右子节点频率之和
HuffmanNode* top = createNode('\0', left->freq + right->freq);
top->left = left;
top->right = right;
// 插入新节点到队列中
insertNode(queue, top);
}
// 返回根节点
return extractMin(queue);
}
// 打印哈夫曼编码
void printHuffmanCodes(HuffmanNode* root, int arr[], int top) {
// 遍历树,生成编码
if (root->left) {
arr[top] = 0;
printHuffmanCodes(root->left, arr, top + 1);
}
if (root->right) {
arr[top] = 1;
printHuffmanCodes(root->right, arr, top + 1);
}
// 当遍历到叶子节点时,打印字符及其编码
if (!root->left && !root->right) {
printf("%c: ", root->data);
for (int i = 0; i < top; i++) {
printf("%d", arr[i]);
}
printf("\n");
}
}
// 主函数
int main() {
char data[] = { 'a', 'b', 'c', 'd', 'e', 'f' }; // 字符集合
int freq[] = { 5, 9, 12, 13, 16, 45 }; // 字符频率
int size = sizeof(data) / sizeof(data[0]); // 字符集合大小
// 构建哈夫曼树
HuffmanNode* root = buildHuffmanTree(data, freq, size);
int arr[100]; // 存储编码的数组
int top = 0; // 记录编码
// 打印哈夫曼编码
printf("哈夫曼编码:\n");
printHuffmanCodes(root, arr, top);
return 0;
}

有点难,啧,我再想想