---

1.UAV路径规划数学模型

【智能算法应用】蜣螂优化算法DBO求解UAV路径规划

2.改进点

Logistics混沌映射

$$X_{{}_{n+1}}=\mu X_{{}_n}(1-X_{{}_n}),X_{{}_n}\in (0,1)\text{\hspace{1em}(1)}$$

动态自适应权重

论文使用Gauss变异替换原有的更新方式,利用边界最大最小值两者作差与高斯分布算子进行交互形成高斯分布数。 这种变异不仅可以跳出局部最优并且可以优化算法的寻优能力,同时,少数麻雀种群会扩大搜索范围,增强种群多样性,有利于搜索潜在区域,从而加快算法的收敛速度。改进后的发现者位置更新公式为：
$${\mathbf{X}}_{i,j}^{t+1}=\{\begin{array}{ll}\left[{\mathbf{X}}_{i,j}^t+\mathbf{\omega }({\mathbf{f}}_{i,j}^t-{\mathbf{X}}_{i,j}^t)\right]\mathbf{\gamma },& R_2<\mathrm{ST}\\ \mathbf{G}(\mathbf{\epsilon })\mathbf{g}+{\mathbf{X}}_{i,j}^t(1-g),& R_2⩾\mathrm{ST}\end{array}\text{\hspace{1em}(2)}$$
参数表述为:
$$\begin{gathered} \omega =\frac{{\mathrm{e}}^{2(1-t/{\mathrm{iter}}_{\max })}-{\mathrm{e}}^{-2(1-t/{\mathrm{iter}}_{\max })}}{{\mathrm{e}}^{2(1-t/{\mathrm{iter}}_{\max })}+{\mathrm{e}}^{-2(1-t/{\mathrm{iter}}_{\max })}} \\ G(\epsilon )=X_{i,j}^t+\gamma (d_1-d_2)g\text{\hspace{1em}(3)} \end{gathered}$$

量子粒子群

量子粒子群算法能够在迭代过程中覆盖整个搜索空间,需要获得一个自适应的势能场,在分析粒子群演化时,粒子群在迭代过程中会收敛至一个点,这个点作为吸引子不断吸引粒子,并且有一定的概率能使得粒子有机会摆脱吸引子的束缚。本文中将采取量子粒子群生成新解的方式替换原有的追随者更新方式:
$${\mathbf{X}}_{i,j}^{t+1}=\{\begin{array}{ll}{\mathbf{P}}_{i,j}^t\pm 0.5{\mathbf{L}}_{i,j}^t\ln \left(\frac{1}{{\mathbf{\mu }}_{i,j}^{t+1}}\right),& i>\frac{n}{2}\\ & \\ {\mathbf{X}}_p^t+|X_{i,j}^t-{\mathbf{X}}_p^t|{\mathbf{A}}^{+}\mathbf{L},& i⩽\frac{n}{2}\end{array}\text{\hspace{1em}(4)}$$
其中，参数表述为:
$$\begin{array}{rl}& {\mathbf{P}}_{i,j}^t={\mathbf{\phi }}_{i,j}^t{\mathbf{X}}_{i,j}^t+\left(1-{\mathbf{\phi }}_{i,j}^t\right){\mathbf{G}}_i^t\\ & L_{i,j}^{\prime }=2a_{{}_t}\mid C_{{}_t}-X_{{}_{i,j}}^{\iota }\mid \\ & a_{{}_t}=a_{{}_0}+\left(a_{{}_1}-a_{{}_0}\right)(T-t)/T\\ & C_{\iota }=\sum _1^M{P}_{i,j}^t\end{array}\text{\hspace{1em}(5)}$$
其中，Pti,j 为吸引子位置; Lti,j 为粒子当前位置与个体平均最优位置的距离; μti,j 均匀分布并且 μti,j ∈(0,1]; Gti 为 t 时刻麻雀种群得全局最优位置; φti,j
为一个随机数∈ (0,1]; Ct 为个体平均最好位置;a1和 a0 分别为收缩扩张因子取1和0. 5。

柯西变异

在种群的每一代更新结束之前将柯西变异算子扰动策略加入到麻雀算法:
$${\mathbf{X}}_{i,j}^{t+1}={\mathbf{X}}_{\mathrm{best}}(t)+\mathrm{cauchy}(0,1){\mathbf{X}}_{\mathrm{best}}(t)\text{\hspace{1em}(6)}$$

3.结果展示

CEC2005测试

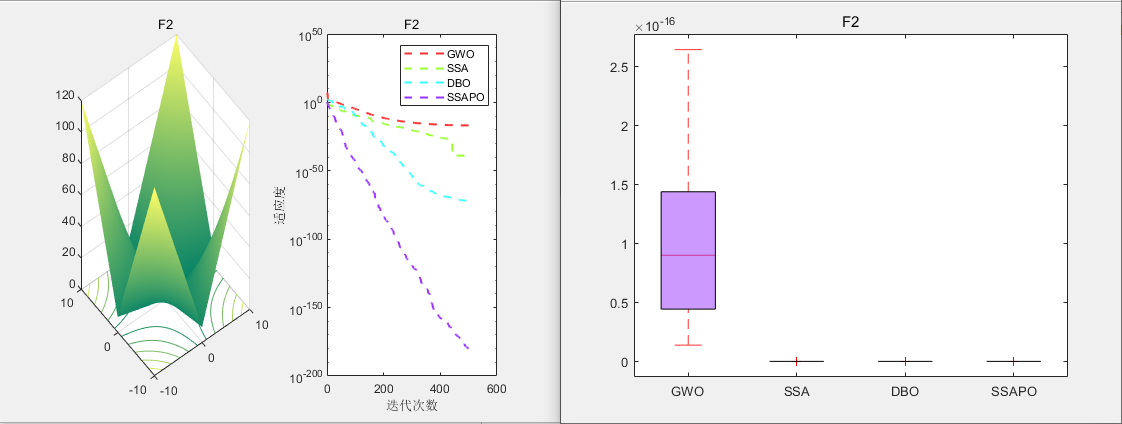
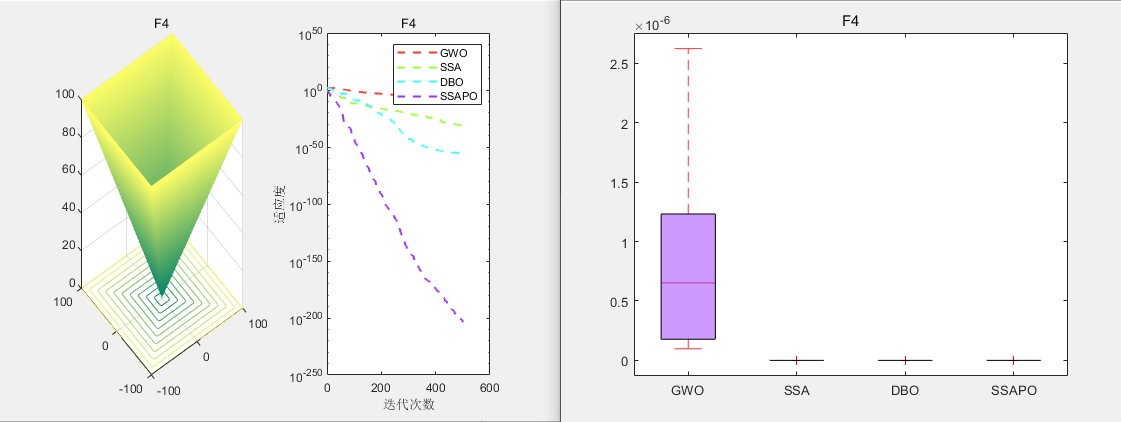
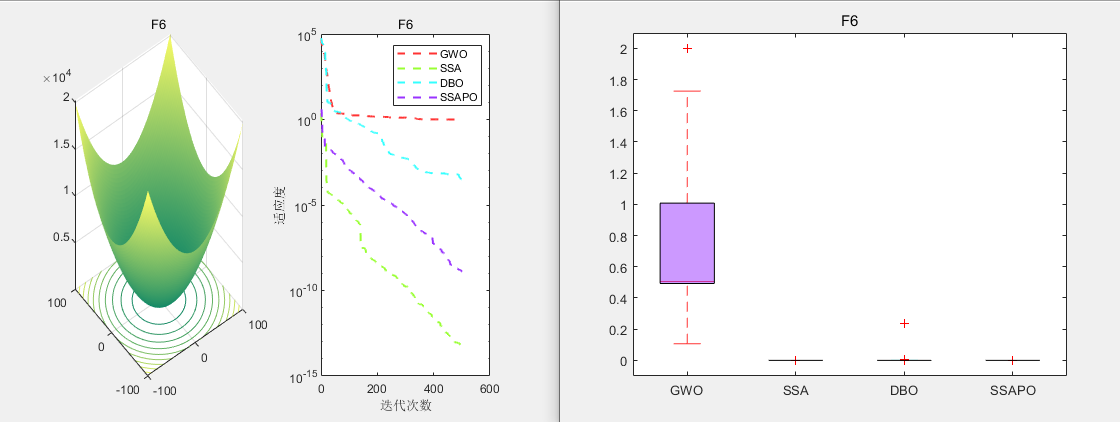
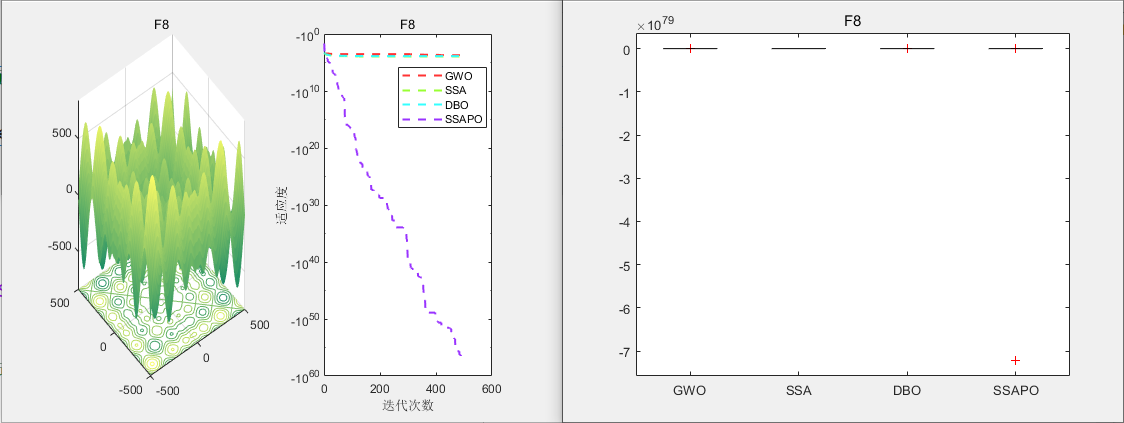
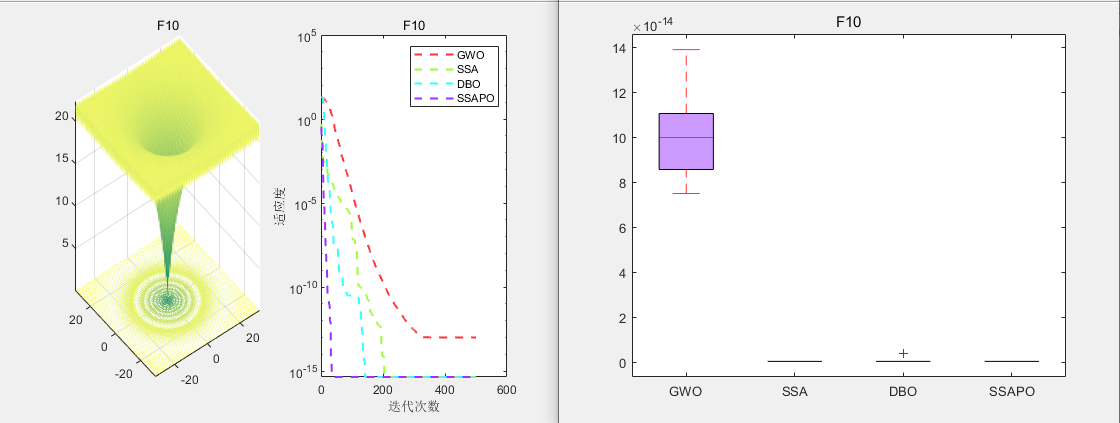
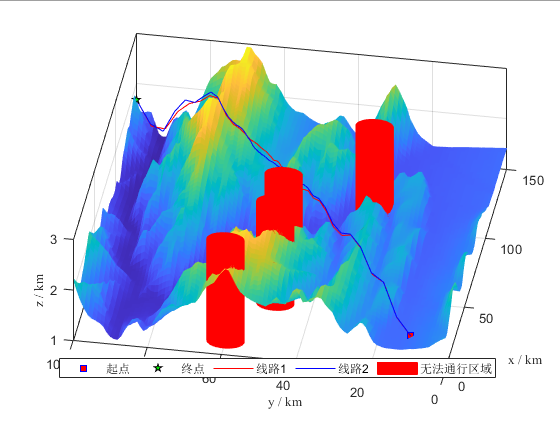
无人机三维路径规划

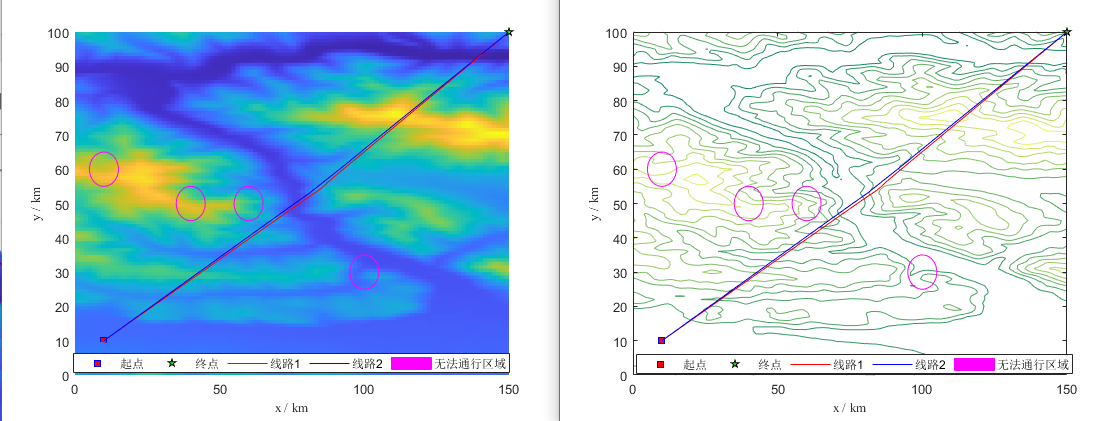
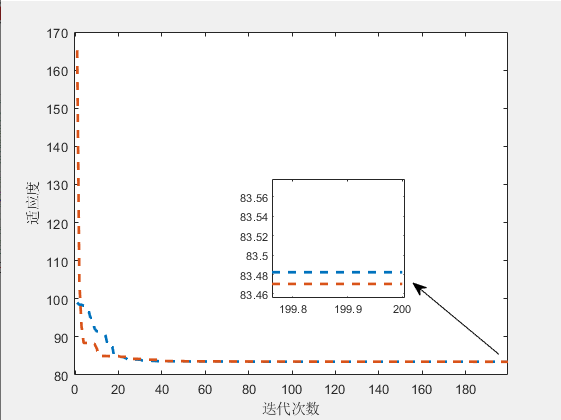
4.参考文献

[1] 吴学礼,王超,赵俊棋,等.改进麻雀算法的无人机三维路径规划[J].科学技术与工程,2024,24(15):6534-6542.

5.代码获取