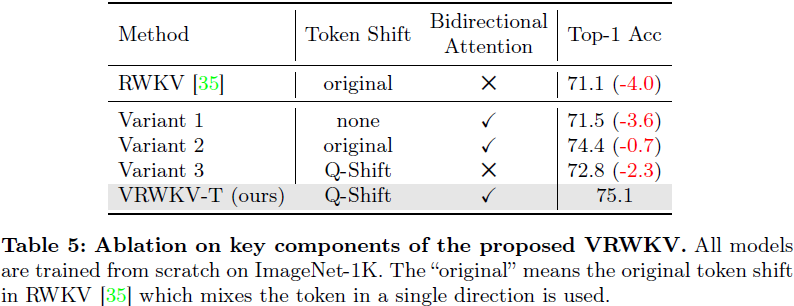
Vision-RWKV: Efficient and Scalable Visual Perception with RWKV-Like Architectures
公和众与号:EDPJ(进 Q 交流群:922230617 或加 VX:CV_EDPJ 进 V 交流群)

目录
0. 摘要
2. 特征聚合机制
3. Vision-RWKV
3.1 总体架构
3.2 线性复杂度双向注意力
3.3 四向标记移位
3.4 扩展稳定性
3.5 模型细节
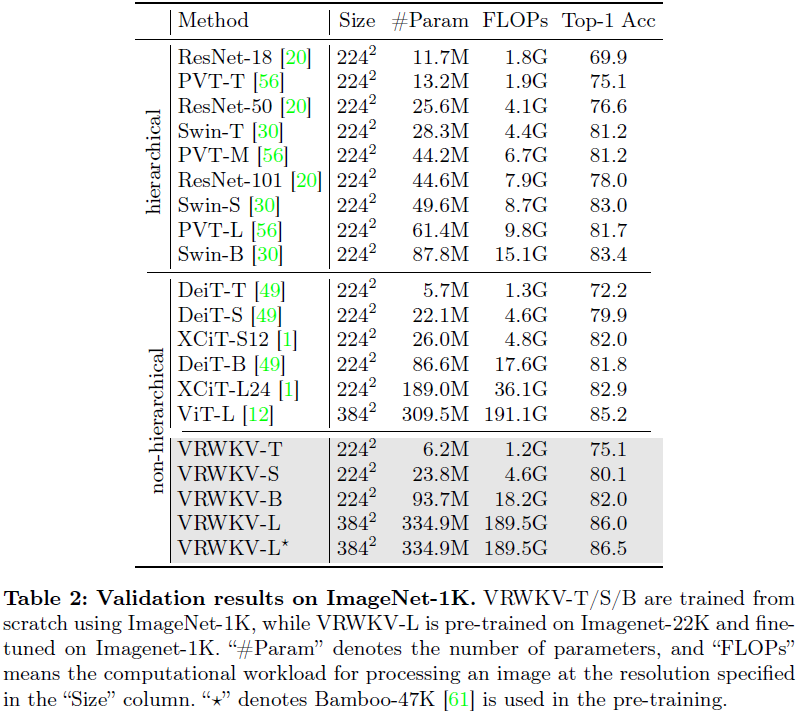
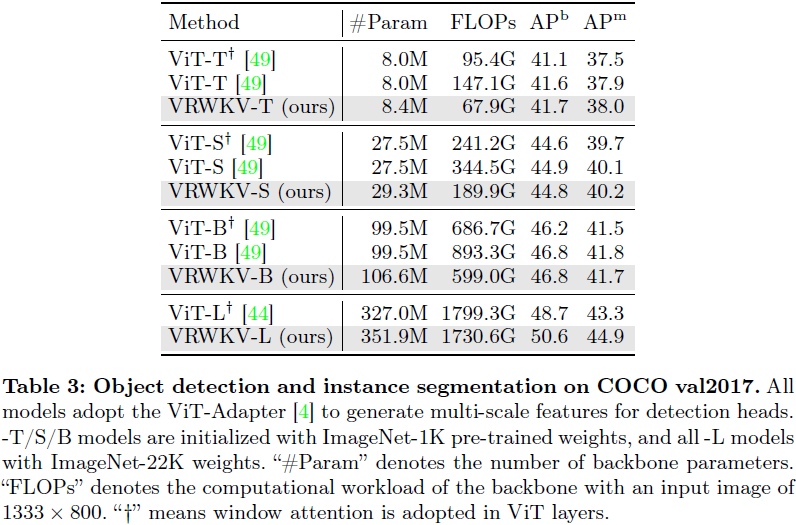
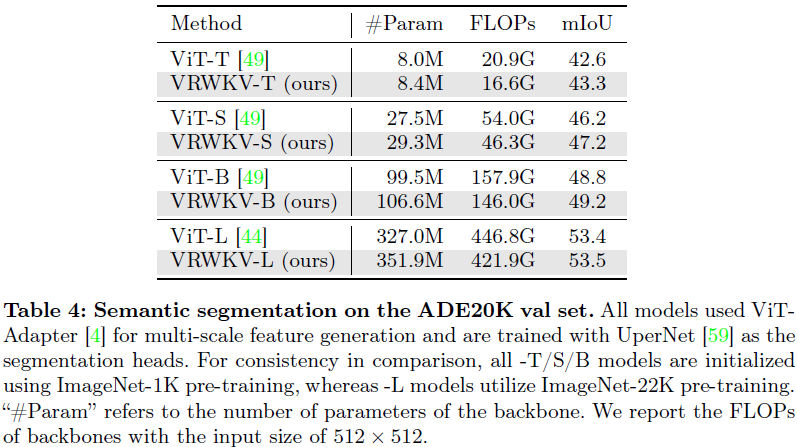
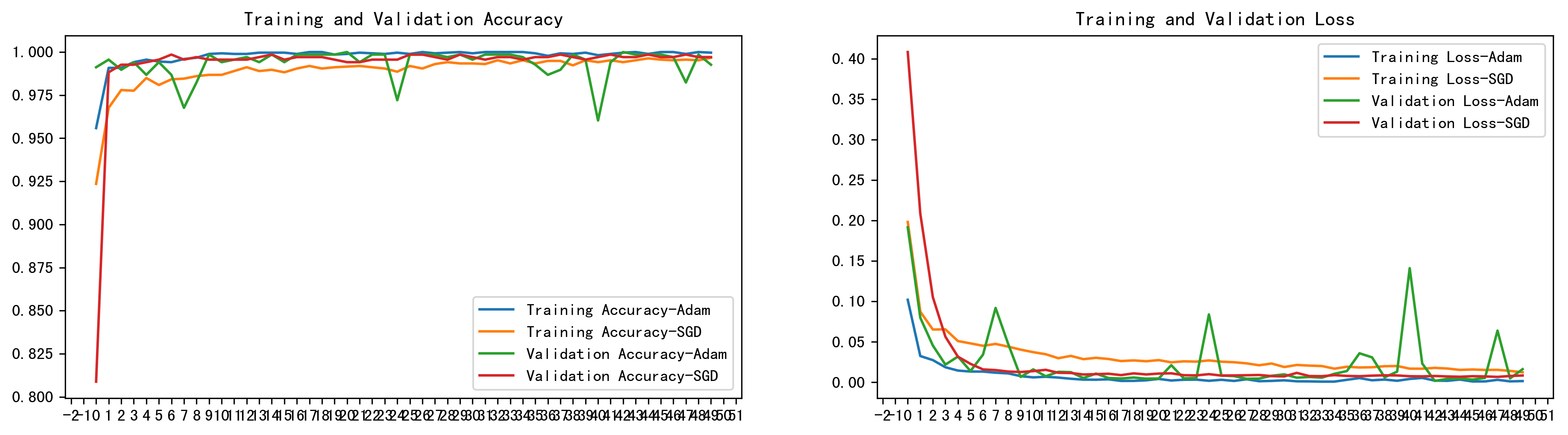
4. 实验
0. 摘要
Transformer 已经彻底改变了计算机视觉和自然语言处理,但其高计算复杂性限制了它们在高分辨率图像处理和长上下文分析中的应用。本文介绍了 Vision-RWKV(VRWKV)模型,这是从在自然语言处理领域使用的 RWKV 模型改编而来,经过必要的修改用于视觉任务。与 Vision Transformer(ViT)类似,我们的模型设计旨在有效处理稀疏输入并展示强大的全局处理能力,同时能够有效扩展,适应大规模参数和广泛数据集。其独特优势在于减少了空间聚合复杂性,使其在处理高分辨率图像时表现出色,无需窗口操作。我们的评估表明,VRWKV 在图像分类方面超过了ViT,并且在处理高分辨率输入时具有显著更快的速度和更低的内存使用。在密集预测任务中,它优于基于窗口的模型,同时保持可比较的速度。这些结果突显了 VRWKV 作为视觉感知任务更高效替代方案的潜力。
项目页面:https://github.com/OpenGVLab/Vision-RWKV

2. 特征聚合机制
在人工智能领域,特征聚合(feature aggregation)的研究引起了广泛关注。对于视觉数据处理,卷积 [24] 以其参数共享和局部感知而闻名,通过滑动计算有效处理大规模数据。尽管传统的 CNN 操作具有这些优势,但面对建模长距离依赖关系的挑战时存在一定困难。为了克服这一问题,先进的卷积操作,如可变形卷积(deformable convolution) [5, 60, 64],增强了CNN 的灵活性,提升了其建模长距离依赖关系的能力。
在自然语言处理领域,基于 RNN 的操作 [13, 34, 37] 以其在序列建模中的有效性而占据主导地位。RNN 和 LSTM 在捕捉时间依赖关系方面表现出色,使它们适用于需要理解序列动态的任务。随后,出现了显著的转变。Transformer 架构的引入 [52] 标志着一个转折点,使得 NLP 和计算机视觉领域都将焦点转向基于注意力的特征聚合。全局注意力机制克服了 CNN 在建模长距离依赖关系和 RNN 在并行计算方面的局限性,尽管以较高的计算成本为代价。
为了解决注意力算子在建模长序列时的高计算成本,研究人员引入了创新技术,如窗口注意力和空间缩减注意力。窗口注意力(Window attention) [6, 30, 51] 限制了自注意力计算在局部窗口内进行,大幅降低了计算复杂度,同时通过窗口级别的交互保留了感受野。另一方面,空间缩减注意力(Spatial reduction attention) [56, 57] 在应用注意力机制之前减少了特征空间的维度,有效降低了计算需求而不显著降低模型性能。
除了优化全局注意力机制的努力外,还探索了具有线性复杂度的各种操作 [15, 35, 36, 46, 47]。例如,RWKV [35] 和 RetNet [47] 利用指数衰减高效建模全局信息,而 SSM [16,17,42,53] 也表现出与序列长度有关的线性复杂性,Mamba 中的修改 [15] 使它们变得依赖于输入。然而,标记(token)之间信息交互效率低下,因此需要辅助模块完成全面的特征聚合。尽管有一些同期努力 [14, 29, 63],将这些源自 NLP 的技术应用于视觉任务仍然是一个挑战,尤其是在保持对更大更复杂视觉模型稳定训练的过程中。
(2023|EMNLP,RWKV,Transformer,RNN,AFT,时间依赖 Softmax,线性复杂度)
3. Vision-RWKV
3.1 总体架构
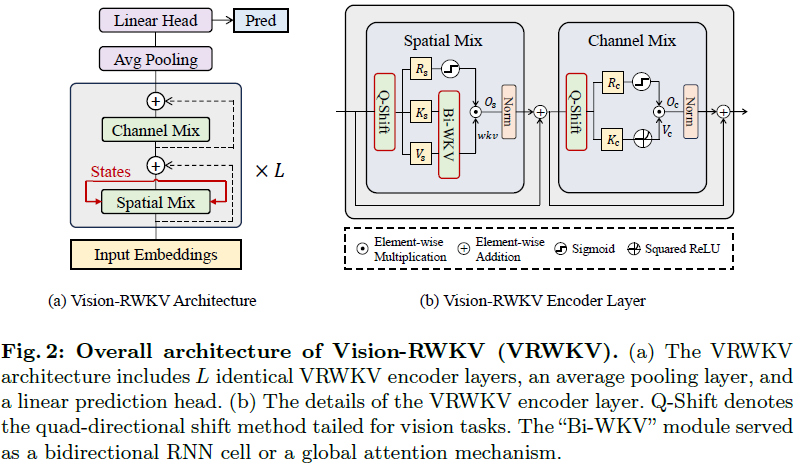
在本节中,我们提出了 Vision-RWKV(VRWKV),一个具有线性复杂度注意力机制的高效视觉编码器。我们的原则是保留原始 RWKV 架构 [35] 的优点,仅进行必要的修改,以使其在视觉任务中灵活应用,支持稀疏输入,并确保在扩展后训练过程的稳定性。我们的 VRWKV 概述如图 2 所示。
VRWKV 采用类似 ViT 的块堆叠图像编码器设计,其中每个块包括一个空间混合模块和一个通道混合模块。空间混合模块作为注意力机制,执行线性复杂度的全局注意力计算,而通道混合模块则作为前馈网络(FFN),在通道维度上执行特征融合。 整个 VRWKV 包括一个补丁(patch)嵌入层和一个由 L 个相同的 VRWKV 编码器层组成的堆叠 ,其中每一层都保持输入分辨率。
数据流。首先,我们将 H×W×3 图像转换为 HW / p^2 个补丁,其中 p 表示补丁大小。线性投影后的补丁添加位置嵌入,以获得形状为 T×C 的图像标记,其中 T = HW / p^2 表示总标记数。然后将这些标记输入到具有 L 层的 VRWKV 编码器中。 在每一层中,标记首先被输入到空间混合模块中,该模块扮演全局注意力机制的角色。具体来说,如图 2(b) 所示,输入标记首先被移位并输入到三个并行线性层中,以获得矩阵 Rs,Ks,Vs ∈ R^(T×C):
![]()
其中,Ks 和 Vs 通过线性复杂度的双向注意力机制传递,计算全局注意力结果 wkv ∈ R^(T×C),并与控制输出 O_s 概率的 σ(R) 相乘:
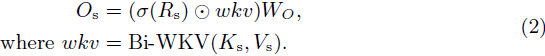
σ 表示 sigmoid 函数,⊙ 表示应用逐元素乘法。Q-Shift 是专门为视觉任务适应的标记移位函数。在进行输出线性投影后,特征通过层归一化 [2] 进行稳定化处理。
![]()
其中,Vc 是经过激活函数后 K 的线性投影,输出 Oc 在输出投影之前也受门控机制 σ(Rc) 控制:
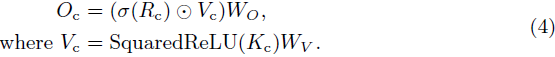
同时,从标记到每个归一化层建立残差连接 [20],以确保在深度网络中训练梯度不会消失。
3.2 线性复杂度双向注意力
与传统的 RWKV [35] 不同,我们对其原始注意力机制进行了以下修改,以适应视觉任务:
- 双向注意力:我们扩展了原始 RWKV 注意力的上限,从当前标记 t 扩展到最后一个标记 T−1,在求和公式中确保每个结果的计算中所有标记都相互可见。因此,原始的因果注意力转变为双向全局注意力。
- 相对偏差:我们计算时间差异 t − i 的绝对值,并除以标记总数 T(表示为 T),以表示不同大小图像中标记的相对偏差。
- 灵活衰减:我们不再限制可学习的衰减参数 w 在指数项中为正,允许指数衰减注意力聚焦不同通道中距离当前标记较远的标记。这种简单而必要的修改实现了全局注意力的计算,并最大程度地保留了 RWKV 低复杂度和对视觉任务的适应性。
与 RWKV 中的注意力类似,我们的双向注意力也可以等价地表达为求和形式(为了清晰起见)和 RNN 形式(在实际实现中)。
求和形式。第 t 个标记的注意力计算结果由以下公式给出:
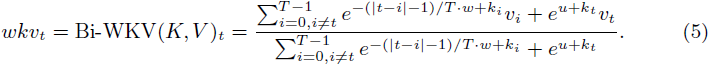
其中,T 表示标记的总数,等于 HW /p^2,w 和 u 是两个 C 维可学习向量,分别表示通道级空间衰减和表示当前标记的奖励。kt 和 vt 表示 K 和 V 的第 t 个特征。
求和公式表明,输出 wkvt 是 V 沿着从 0 到 T−1 的标记维度的加权和,得到一个 C 维向量。它表示对第 t 个标记应用注意力操作后得到的结果。权重由空间衰减向量 w、标记之间的相对偏差 (|t−i|1)/T 和 ki 共同决定。
RNN 形式。在实际实现中,上述方程(5)可以通过 RNN 形式的递归公式来转换,每个标记的结果可以通过固定数量的 FLOP 来获取。通过以 t 为边界分割方程(5)中的分母和分子的求和项,我们可以获得可通过递归计算的 4 个隐藏状态:
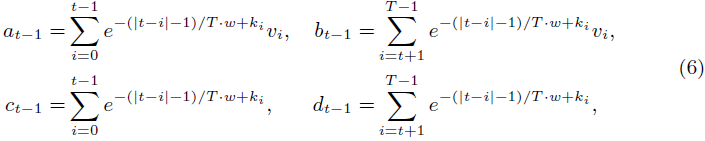
隐藏状态的更新仅需要添加或减去一个求和项,并乘以或除以 e^{-w/T}。然后第 t 个结果可以表示为:
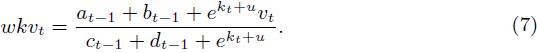
每个更新步骤为一个标记产生一个注意力结果(即 wkvt),因此整个 wkv 矩阵需要 T 步骤。
当输入 K 和 V 是形状为 T×C 的矩阵时,计算 wkv 矩阵的计算成本如下:
![]()
其中,数字 13 近似地来自 (a, b, c, d) 的更新、指数的计算以及 wkvt 的计算。T 是总的更新步数,等于图像标记的数量。上述近似显示了正向过程的复杂度为 O(TC)。操作符的反向传播仍可以表示为更复杂的 RNN 形式,其计算复杂度为 O(TC)。具体的反向传播公式在附录中提供。
3.3 四向标记移位
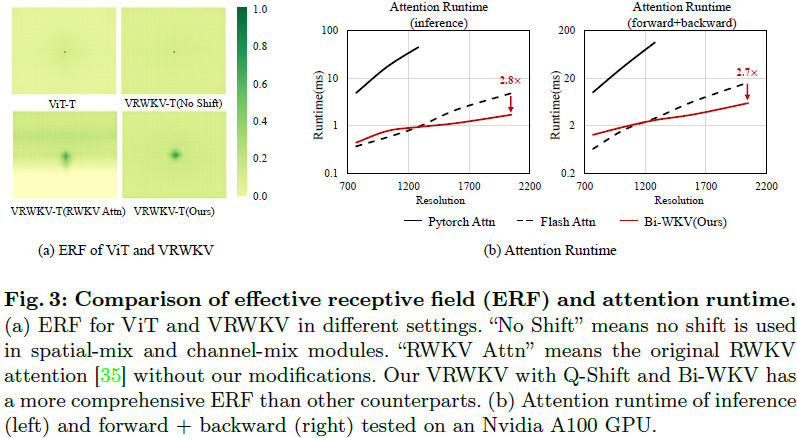
通过引入指数衰减机制,全局注意力的复杂度可以从二次降低到线性,极大增强了模型在高分辨率图像中的计算效率。然而,一维衰减与二维图像中的邻近关系不对齐。因此,我们在每个空间混合和通道混合模块的第一步引入了四向标记移位(Q-Shift)。Q-Shift 操作允许所有标记与它们的邻近标记进行线性插值和移位,如下所示:
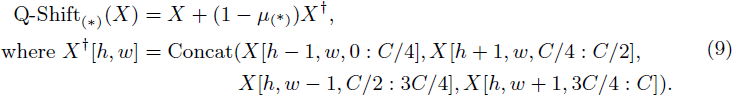
下标 (*) ∈ {R, K, V} 表示由可学习向量 μ(*) 控制的 X 和 X† 的三个插值,用于后续计算 R, K, V。h 和 w 表示标记 X 的行和列索引,“:” 是一个切片操作,不包括结束索引。Q-Shift 使不同通道的注意力机制在不引入过多额外 FLOP 的情况下,获得专注于内部邻近标记的优势。Q-Shift 操作还增加了每个标记的接收域,极大增强了后续层中标记的覆盖范围。
3.4 扩展稳定性
模型层数增加和递归过程中指数项的累积都可能导致模型输出的不稳定性,并影响训练过程的稳定性。为了减轻这种不稳定性,我们采用了两种简单而有效的修改来稳定模型的扩展。
- 有界指数:随着输入分辨率的增加,指数衰减和增长很快超出浮点数范围。因此,我们通过标记数量来除以指数项(例如 exp(−(|t − i| − 1)/T · w)),使最大衰减和增长受到限制。
- 额外的层归一化:当模型变得更深时,我们在注意力机制和 Squared ReLU 操作后直接添加层归一化 [2],以防止模型输出溢出。这两种修改使得输入分辨率和模型深度的扩展变得稳定,使得大型模型能够稳定训练和收敛。我们还引入层尺度(layer scale) [50],有助于模型在扩展时的稳定性。
3.5 模型细节
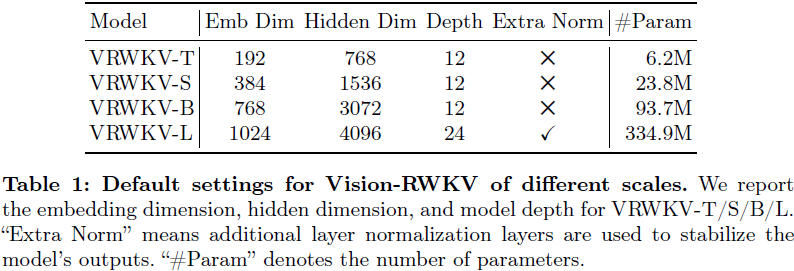
在 ViT 的基础上,包括嵌入维度、线性投影中的隐藏维度和深度等 VRWKV 变体的超参数在表 1 中进行了指定。由于 VRWKV-L 模型的深度增加,根据第 3.4 节讨论的内容,在适当位置引入了额外的层归一化,以确保输出的稳定性。
4. 实验