目录
L3-001 凑零钱
输入格式:
输出格式:
输入样例 1:
输出样例 1:
输入样例 2:
输出样例 2:
L3-002 特殊堆栈
输入格式:
输出格式:
输入样例:
输出样例:
L3-003 社交集群
输入格式:
输出格式:
输入样例:
输出样例:
L3-004 肿瘤诊断
输入格式:
输出格式:
输入样例:
输出样例:
L3-005 垃圾箱分布
输入格式:
输出格式:
输入样例1:
输出样例1:
输入样例2:
输出样例2:
L3-006 迎风一刀斩
输入格式:
输出格式:
输入样例:
输出样例:
L3-007 天梯地图
输入格式:
输出格式:
输入样例1:
输出样例1:
输入样例2:
输出样例2:
L3-008 喊山
输入格式:
输出格式:
输入样例:
输出样例:
L3-009 长城
输入格式:
输出格式:
输入样例:
输出样例:
L3-010 是否完全二叉搜索树
输入格式:
输出格式:
输入样例1:
输出样例1:
输入样例2:
输出样例2:
L3-011 直捣黄龙
输入格式:
输出格式:
输入样例:
输出样例:
L3-012 水果忍者
输入格式:
输出格式:
输入样例:
输出样例:
L3-013 非常弹的球
输入格式:
输出格式:
输入样例:
输出样例:
L3-014 周游世界
输入格式:
输出格式:
输入样例:
输出样例:
L3-015 球队“食物链”
输入格式:
输出格式:
输入样例1:
输出样例1:
输入样例2:
输出样例2:
L3-016 二叉搜索树的结构
输入格式:
输出格式:
输入样例:
输出样例:
L3-017 森森快递
输入格式:
输出格式:
输入样例:
输出样例:
样例提示:我们选择执行最后两张订单,即把5公斤货从城市4运到城市2,并且把2公斤货从城市4运到城市5,就可以得到最大运输量7公斤。
L3-018 森森美图
输入格式:
输出格式:
输入样例:
输出样例:
L3-019 代码排版
输入格式:
输出格式:
输入样例:
输出样例:
L3-020 至多删三个字符
输入格式:
输出格式:
输入样例:
输出样例:
L3-021 神坛
输入格式:
输出格式:
输入样例:
输出样例:
样例解释
L3-022 地铁一日游
输入格式:
输出格式:
输入样例:
输出样例:
L3-023 计算图
输入格式:
输出格式:
输入样例:
输出样例:
L3-024 Oriol和David
输入格式:
输出格式:
输入样例:
输出样例:
评分方式:
L3-025 那就别担心了
输入格式:
输出格式:
输入样例 1:
输出样例 1:
输入样例 2:
输出样例 2:
输入格式:
输出格式:
输入样例:
输出样例:
样例解释:
L3-027 可怜的复杂度
输入格式:
输出格式:
输入样例:
输出样例:
L3-028 森森旅游
输入格式:
输出格式:
输入样例:
输出样例:
样例解释:
L3-029 还原文件
输入格式:
输出格式:
输入样例:
输出样例:
L3-030 可怜的简单题
输入格式:
输出格式:
输入样例 1:
输出样例 1:
输入样例 2:
输出样例 2:
L3-031 千手观音
输入格式:
输出格式:
输入样例:
输出样例:
L3-032 关于深度优先搜索和逆序对的题应该不会很难吧这件事
背景知识
深度优先搜索与 DFS 序
逆序对
问题求解
输入格式
输出格式
样例输入 1
样例输出 1
样例输入 2
样例输出 2
样例解释
L3-033 教科书般的亵渎
输入格式:
输出格式:
输入样例 1:
输出样例 1:
样例解释 1:
输入样例 2:
输出样例 2:
样例解释 2:
输入样例 3:
输出样例 3:
输入样例 4:
输出样例 4:
L3部分的题目一般来说就是困难题目了,有些题目没有题解呜呜呜,比较适合对算法有兴趣的小伙伴攻坚,要消耗大量时间,适合先天竞赛圣体的高手刷题。
L3-001 凑零钱
分数 80
全屏浏览
切换布局
作者 陈越
单位 浙江大学
韩梅梅喜欢满宇宙到处逛街。现在她逛到了一家火星店里,发现这家店有个特别的规矩:你可以用任何星球的硬币付钱,但是绝不找零,当然也不能欠债。韩梅梅手边有 104 枚来自各个星球的硬币,需要请你帮她盘算一下,是否可能精确凑出要付的款额。
输入格式:
输入第一行给出两个正整数:N(≤104)是硬币的总个数,M(≤102)是韩梅梅要付的款额。第二行给出 N 枚硬币的正整数面值。数字间以空格分隔。
输出格式:
在一行中输出硬币的面值 V1≤V2≤⋯≤Vk,满足条件 V1+V2+...+Vk=M。数字间以 1 个空格分隔,行首尾不得有多余空格。若解不唯一,则输出最小序列。若无解,则输出 No Solution。
注:我们说序列{ A[1],A[2],⋯ }比{ B[1],B[2],⋯ }“小”,是指存在 k≥1 使得 A[i]=B[i] 对所有 i<k 成立,并且 A[k]<B[k]。
输入样例 1:
8 9
5 9 8 7 2 3 4 1
输出样例 1:
1 3 5
输入样例 2:
4 8
7 2 4 3
输出样例 2:
No Solution//非常经典的01背包问题
//背包容量就是款额
//物品就是对应的银币,相当于物品的价值和重量一样
#include <iostream>
#include<algorithm>
using namespace std;
bool cmp(int a,int b){
return a>b;
}
int main(){
int n,m;
cin>>n>>m;
int v[n+1];
for(int i=1;i<=n;i++){
cin>>v[i];
}
int dp[n+1][m+1];
int suanze[n+1][m+1];//这个是用来储存我是否选择了这个硬币
for(int i=1;i<=n;i++){
for(int j=1;j<=m;j++){
suanze[i][j]=0;
}
}
for(int i=0;i<=n;i++)
dp[i][0]=0;
for(int i=0;i<=m;i++)
dp[0][i]=0;
//由于我们需要输出最小的编号,那么我们选择对数组进行降序排序
sort(v+1,v+n+1,cmp);
for(int i=1;i<=n;i++){
for(int j=m;j>=0;j--){
if(j>=v[i]){
dp[i][j]=max(dp[i-1][j],dp[i-1][j-v[i]]+v[i]);
//由于我们需要后面的编号,等于的时候必须要更新数组
if(dp[i-1][j]<=dp[i-1][j-v[i]]+v[i])
suanze[i][j]=1;
}
else
dp[i][j]=dp[i-1][j];
}
}
if(dp[n][m]!=m)
cout<<"No Solution";
else{
vector<int>ans;
int id=n;
while (m) {
if(suanze[id][m]){
ans.push_back(v[id]);
m-=v[id];
}
--id;
}
for(int i = 0;i<ans.size();++i){
if(i)
cout << " ";
cout << ans[i];
}
cout << endl;
}
}
L3-002 特殊堆栈
分数 80
全屏浏览
切换布局
作者 陈越
单位 浙江大学
堆栈是一种经典的后进先出的线性结构,相关的操作主要有“入栈”(在堆栈顶插入一个元素)和“出栈”(将栈顶元素返回并从堆栈中删除)。本题要求你实现另一个附加的操作:“取中值”——即返回所有堆栈中元素键值的中值。给定 N 个元素,如果 N 是偶数,则中值定义为第 N/2 小元;若是奇数,则为第 (N+1)/2 小元。
输入格式:
输入的第一行是正整数 N(≤105)。随后 N 行,每行给出一句指令,为以下 3 种之一:
Push key
Pop
PeekMedian
其中 key 是不超过 105 的正整数;Push 表示“入栈”;Pop 表示“出栈”;PeekMedian 表示“取中值”。
输出格式:
对每个 Push 操作,将 key 插入堆栈,无需输出;对每个 Pop 或 PeekMedian 操作,在一行中输出相应的返回值。若操作非法,则对应输出 Invalid。
输入样例:
17
Pop
PeekMedian
Push 3
PeekMedian
Push 2
PeekMedian
Push 1
PeekMedian
Pop
Pop
Push 5
Push 4
PeekMedian
Pop
Pop
Pop
Pop
输出样例:
Invalid
Invalid
3
2
2
1
2
4
4
5
3
Invalid//我嘞个爆弹,这道题是我见到最简单的了
//核心就是进出,取中值只需要多设一个栈即可
//我类个去他还要排序,其实也简单多设一个数组就好了
//我靠超时了,注意不能每次找中值时都排序,我们可以在弹出或者插入时采用二分查找缩短时间
#include<iostream>
#include<stack>
#include<vector>
#include<algorithm>
using namespace std;
int main(){
int n;
stack<int> s;
vector<int> v;
cin>>n;
for(int i=0;i<n;i++){
string str;
cin>>str;
if(str=="Pop"){
if(s.size()==0)
cout<<"Invalid"<<endl;
else{
cout<<s.top()<<endl;
v.erase(lower_bound(v.begin(),v.end(),s.top()));//删除对应位置元素
s.pop();
}
}
else if(str=="PeekMedian"){
if(s.size()==0){
cout<<"Invalid"<<endl;
}
else{
int t=(s.size()+1)/2;//第几小
cout<<v[t-1]<<endl;
}
}
else{
int x;
cin>>x;
s.push(x);
v.insert(lower_bound(v.begin(),v.end(),x),x);//对应位置插入
}
}
}
L3-003 社交集群
分数 60
全屏浏览
切换布局
作者 陈越
单位 浙江大学
当你在社交网络平台注册时,一般总是被要求填写你的个人兴趣爱好,以便找到具有相同兴趣爱好的潜在的朋友。一个“社交集群”是指部分兴趣爱好相同的人的集合。你需要找出所有的社交集群。
输入格式:
输入在第一行给出一个正整数 N(≤1000),为社交网络平台注册的所有用户的人数。于是这些人从 1 到 N 编号。随后 N 行,每行按以下格式给出一个人的兴趣爱好列表:
Ki: hi[1] hi[2] ... hi[Ki]
其中Ki(>0)是兴趣爱好的个数,hi[j]是第j个兴趣爱好的编号,为区间 [1, 1000] 内的整数。
输出格式:
首先在一行中输出不同的社交集群的个数。随后第二行按非增序输出每个集群中的人数。数字间以一个空格分隔,行末不得有多余空格。
输入样例:
8
3: 2 7 10
1: 4
2: 5 3
1: 4
1: 3
1: 4
4: 6 8 1 5
1: 4
输出样例:
3
4 3 1//题目难度不大额简单点来说就是并查集
#include<iostream>
#include<algorithm>
using namespace std;
int fu[1001];
int find(int x){
if(fu[x]==x)
return x;
else
return find(fu[x]);
}
void un(int a,int b){
int f1=find(a);
int f2=find(b);
fu[f2]=f1;
}
int main(){
int n;
cin>>n;
for(int i=0;i<=1000;i++){
fu[i]=i;
}
int ren[1001];//用来记录某个人的爱好,取一个就行了
int jiqunshu[1001]={0};//用来记录对应集群的人数
for(int i=0;i<n;i++){
int m;
char c;
cin>>m>>c;
int a1;
cin>>a1;//读第一个数字
ren[i+1]=a1;
for(int j=1;j<m;j++){
int a2;
cin>>a2;
un(a1,a2);
}
}
int num=0;
for(int i=1;i<=n;i++){
int x=find(ren[i]);
jiqunshu[x]++;
}
for(int i=1;i<=1000;i++){
if(jiqunshu[i]!=0)
num++;
}
sort(jiqunshu+1,jiqunshu+1001);
//排完序倒着输出就好了
cout<<num<<endl;
cout<<jiqunshu[1000];
for(int i=999;i>1000-num;i--){
cout<<" "<<jiqunshu[i];
}
}
L3-004 肿瘤诊断
分数 60
全屏浏览
切换布局
作者 陈越
单位 浙江大学
在诊断肿瘤疾病时,计算肿瘤体积是很重要的一环。给定病灶扫描切片中标注出的疑似肿瘤区域,请你计算肿瘤的体积。
输入格式:
输入第一行给出4个正整数:M、N、L、T,其中M和N是每张切片的尺寸(即每张切片是一个M×N的像素矩阵。最大分辨率是1286×128);L(≤60)是切片的张数;T是一个整数阈值(若疑似肿瘤的连通体体积小于T,则该小块忽略不计)。
最后给出L张切片。每张用一个由0和1组成的M×N的矩阵表示,其中1表示疑似肿瘤的像素,0表示正常像素。由于切片厚度可以认为是一个常数,于是我们只要数连通体中1的个数就可以得到体积了。麻烦的是,可能存在多个肿瘤,这时我们只统计那些体积不小于T的。两个像素被认为是“连通的”,如果它们有一个共同的切面,如下图所示,所有6个红色的像素都与蓝色的像素连通。

输出格式:
在一行中输出肿瘤的总体积。
输入样例:
3 4 5 2
1 1 1 1
1 1 1 1
1 1 1 1
0 0 1 1
0 0 1 1
0 0 1 1
1 0 1 1
0 1 0 0
0 0 0 0
1 0 1 1
0 0 0 0
0 0 0 0
0 0 0 1
0 0 0 1
1 0 0 0
输出样例:
26//我勒个骚刚,三维dfs牛魔是吧
//简单点来说就是把这个图像看成是一个立体的空间
//然后嘞就是从每一个点开始深搜,因为有些点可能没联通
//然后就是深搜是六个方向我们可以实现写好
//深搜好像会爆炸,改为广搜
//还是不行好像是三维数组都会超,只能强行压缩成二维
//不改了草
#include<iostream>
#include<vector>
#include<queue>
using namespace std;
struct fangxiang{
int k,x,y;
};//用结构体来储存坐标
int photo[60][1286][128];//直接根据题目分配空间
int dir[6][3]={{1,0,0},{0,1,0},{0,0,1},{-1,0,0},{0,-1,0},{0,0,-1}};
//因为是六个方向三个坐标
int M, N, L, T;
int getArea(int k,int x,int y){
int result=0;
queue<struct fangxiang> q;
struct fangxiang t;
t.k=k;
t.x=x;
t.y=y;
if(photo[k][x][y]==1){
photo[k][x][y]=0;//防止重复
result++;
}
q.push(t);
while(q.size()!=0){
t=q.front();
q.pop();
for(int i=0;i<6;i++){
//这里要记得边界判断
if(t.k+dir[i][0]>=0&&t.k+dir[i][0]<=L&&t.x+dir[i][1]>=0&&t.x+dir[i][1]<=M&&t.y+dir[i][2]<=N&&t.y+dir[i][2]>=0){
struct fangxiang tt;
tt.k=t.k+dir[i][0];
tt.x=t.x+dir[i][1];
tt.y=t.y+dir[i][2];
if(photo[tt.k][tt.x][tt.y]==0)
continue;
q.push(tt);
if(photo[tt.k][tt.x][tt.y]==1){
photo[tt.k][tt.x][tt.y]=0;
result++;
}
}
}
}
return result;
}
int main() {
cin>>M>>N>>L>>T;
for(int k=0;k<L;k++){
for(int i=0;i<M;i++){
for(int j=0;j<N;j++){
cin>>photo[k][i][j];
}
}
}
int result=0;
for(int k=0;k<L;k++){
for(int i=0;i<M;i++){
for(int j=0;j<N;j++){
//这里再压缩
if(photo[k][i][j]==0)
continue;
int area=getArea(k,i,j);
if(area>=T)
result+=area;
}
}
}
cout<<result;
}
L3-005 垃圾箱分布
分数 60
全屏浏览
切换布局
作者 陈越
单位 浙江大学
大家倒垃圾的时候,都希望垃圾箱距离自己比较近,但是谁都不愿意守着垃圾箱住。所以垃圾箱的位置必须选在到所有居民点的最短距离最长的地方,同时还要保证每个居民点都在距离它一个不太远的范围内。
现给定一个居民区的地图,以及若干垃圾箱的候选地点,请你推荐最合适的地点。如果解不唯一,则输出到所有居民点的平均距离最短的那个解。如果这样的解还是不唯一,则输出编号最小的地点。
输入格式:
输入第一行给出4个正整数:N(≤103)是居民点的个数;M(≤10)是垃圾箱候选地点的个数;K(≤104)是居民点和垃圾箱候选地点之间的道路的条数;DS是居民点与垃圾箱之间不能超过的最大距离。所有的居民点从1到N编号,所有的垃圾箱候选地点从G1到GM编号。
随后K行,每行按下列格式描述一条道路:
P1 P2 Dist
其中P1和P2是道路两端点的编号,端点可以是居民点,也可以是垃圾箱候选点。Dist是道路的长度,是一个正整数。
输出格式:
首先在第一行输出最佳候选地点的编号。然后在第二行输出该地点到所有居民点的最小距离和平均距离。数字间以空格分隔,保留小数点后1位。如果解不存在,则输出No Solution。
输入样例1:
4 3 11 5
1 2 2
1 4 2
1 G1 4
1 G2 3
2 3 2
2 G2 1
3 4 2
3 G3 2
4 G1 3
G2 G1 1
G3 G2 2
输出样例1:
G1
2.0 3.3
输入样例2:
2 1 2 10
1 G1 9
2 G1 20
输出样例2:
No Solution//第一眼就是最短路径迪杰斯特拉算法
//直接开写
//样例4数据有问题啊,不是我的错,大佬都那么说了那我就直接开超,方法对的就好了
#include <iostream>
#include <vector>
#include<string>
#define INF 1 << 30
using namespace std;
int N, M, K, D;
void dijkstra(int start,int map[1020][1020],int cnt[2]) {
int dist[N+M+1]={INF};
int visit[N+M+1]={0};
dist[start]=0;
for(int i=1;i<N+M+1;i++) {
dist[i]=map[start][i];
}
while (true){
int v;
int min=INF;
//找出最小边
for (int j=1;j<=N+M;j++){
if(visit[j]==0&&dist[j]<min) {
min=dist[j];
v=j;
}
}
if(min==INF)
break;
visit[v]=1;
for(int i=1;i<N+M+1;i++){
if (dist[i]>dist[v]+map[v][i])
dist[i]=dist[v]+map[v][i];
}
}
// 统计
for(int i=1;i<=N;i++){
if(dist[i]>D){
cnt[0]=0;
cnt[1]=0;
break;
}
if(dist[i]<cnt[1])
cnt[1]=dist[i];
cnt[0]+=dist[i];
}
}
int main() {
cin>>N>>M>>K>>D;
int map[1020][1020];
fill(map[0],map[0]+1020*1020,INF);
for(int i=0;i<K;i++) {
string startstring;
string endstring;
int dist,start,end;
cin>>startstring>>endstring>>dist;
if(startstring[0]=='G')
start=startstring[1]-'0'+N;
else
start=startstring[0]-'0';
if(endstring[0]=='G')
end=endstring[1]-'0'+N;
else
end=endstring[0]-'0';
map[start][end]=dist;
map[end][start]=dist;
}
double mindis=0;
double avg_dis=INF;
int minindex;
for(int i=N+1;i<=N+M;i++) {
int cnt[2]={0,INF};
dijkstra(i,map,cnt);
if(cnt[0]!=0&&(mindis<cnt[1]||(mindis==cnt[1]&&((double)cnt[0]/N)<avg_dis))){
mindis=cnt[1];
avg_dis=(double)cnt[0]/N;
minindex=i;
}
}
if(avg_dis==INF)
cout<<"No Solution";
else{
cout<<"G"<<minindex-N<<endl;
printf("%.1f %.1f", mindis, avg_dis);
}
}
L3-006 迎风一刀斩
分数 80
全屏浏览
切换布局
作者 刘汝佳
单位 北京尔宜居科技有限责任公司
迎着一面矩形的大旗一刀斩下,如果你的刀够快的话,这笔直一刀可以切出两块多边形的残片。反过来说,如果有人拿着两块残片来吹牛,说这是自己迎风一刀斩落的,你能检查一下这是不是真的吗?
注意摆在你面前的两个多边形可不一定是端端正正摆好的,它们可能被平移、被旋转(逆时针90度、180度、或270度),或者被(镜像)翻面。
这里假设原始大旗的四边都与坐标轴是平行的。
输入格式:
输入第一行给出一个正整数N(≤20),随后给出N对多边形。每个多边形按下列格式给出:
kx1y1⋯xkyk
其中k(2<k≤10)是多边形顶点个数;(xi,yi)(0≤xi,yi≤108)是顶点坐标,按照顺时针或逆时针的顺序给出。
注意:题目保证没有多余顶点。即每个多边形的顶点都是不重复的,任意3个相邻顶点不共线。
输出格式:
对每一对多边形,输出YES或者NO。
输入样例:
8
3 0 0 1 0 1 1
3 0 0 1 1 0 1
3 0 0 1 0 1 1
3 0 0 1 1 0 2
4 0 4 1 4 1 0 0 0
4 4 0 4 1 0 1 0 0
3 0 0 1 1 0 1
4 2 3 1 4 1 7 2 7
5 10 10 10 12 12 12 14 11 14 10
3 28 35 29 35 29 37
3 7 9 8 11 8 9
5 87 26 92 26 92 23 90 22 87 22
5 0 0 2 0 1 1 1 2 0 2
4 0 0 1 1 2 1 2 0
4 0 0 0 1 1 1 2 0
4 0 0 0 1 1 1 2 0
输出样例:
YES
NO
YES
YES
YES
YES
NO
YES//这题目也是相当的抽象啊
//首先我们需要知道一个矩形可以分几种情况切成多边形
//然后就是判断非直角边的长度一致
//哎还没结束由于题目的限制,多边形最多只有一条边不和坐标轴平行
#include<iostream>
#include<vector>
using namespace std;
int diancheng(pair<int,int> a,pair<int,int> b){
return a.first*b.first+a.second*b.second;
}
pair<int,int> jianfa(pair<int,int> a,pair<int,int> b){
pair<int,int> t;
t.first=a.first-b.first;
t.second=a.second-b.second;
return t;
}
int main(){
int n;
cin>>n;
for(int i=1;i<=n;i++){
int n1,n2;//第一、二个多边形
vector<pair<int,int>> v1,v2;
cin>>n1;
for(int j=1;j<=n1;j++){
pair<int,int> t;
cin>>t.first>>t.second;
v1.push_back(t);
}
cin>>n2;
for(int j=1;j<=n2;j++){
pair<int,int> t;
cin>>t.first>>t.second;
v2.push_back(t);
}
if(!(n1==4&&n2==4||n1==3&&n2==3||max(n1,n2)==5&&min(n1,n2)==3||max(n1,n2)==4&&min(n1,n2)==3)){
//如果不是上述情况的任意一种就可以走了
cout<<"NO"<<endl;
continue;
}
int p1,p2,p3,p4;//p1,p2是第一个多边形的非直角边的点的编号,p3、p4是第二个
int cnt1=0;
int cnt2=0;//这个是和坐标轴不平行的边的条数
int num1=0;
int num2=0;//这个是直角的个数
p1=p2=p3=p4=-1;//初始化一下
int p11,p22,p33,p44;
p11=p22=p33=p44=-1;//这个是直角边
for(int j=0;j<n1;j++){
int t=diancheng(jianfa(v1[j],v1[(j+1)%n1]),jianfa(v1[(j+2)%n1],v1[(j+1)%n1]));
if(t!=0){//说明这三个点形成的角非直角
if(p1==-1)
p1=(j+1)%n1;
else
p2=(j+1)%n1;
}
else{
num1++;
if(p11==-1)
p11=(j+1)%n1;
else
p22=(j+1)%n1;
}
if(v1[j].first!=v1[(j+1)%n1].first&&v1[j].second!=v1[(j+1)%n1].second)
cnt1++;
}
for(int j=0;j<n2;j++){
int t=diancheng(jianfa(v2[j],v2[(j+1)%n2]),jianfa(v2[(j+2)%n2],v2[(j+1)%n2]));
if(t!=0){//说明这三个点形成的角非直角
if(p3==-1)
p3=(j+1)%n2;
else
p4=(j+1)%n2;
}
else{
num2++;
if(p33==-1)
p33=(j+1)%n2;
else
p44=(j+1)%n2;
}
if(v2[j].first!=v2[(j+1)%n2].first&&v2[j].second!=v2[(j+1)%n2].second)
cnt2++;
}
if(cnt1>1||cnt2>1){
cout<<"NO"<<endl;
continue;
}
if(num1==4&&num2==4){//两个矩形特判(因为点都是顺时针或者逆时针给出的,所以取相邻三个点即可)
int t1 = (v1[0].first-v1[1].first)*(v1[0].first-v1[1].first)+(v1[0].second-v1[1].second)*(v1[0].second-v1[1].second);
int t2 = (v1[1].first-v1[2].first)*(v1[1].first-v1[2].first)+(v1[1].second-v1[2].second)*(v1[1].second-v1[2].second);
int t3 = (v2[0].first-v2[1].first)*(v2[0].first-v2[1].first)+(v2[0].second-v2[1].second)*(v2[0].second-v2[1].second);
int t4 = (v2[1].first-v2[2].first)*(v2[1].first-v2[2].first)+(v2[1].second-v2[2].second)*(v2[1].second-v2[2].second);
if(t1==t3||t2==t3||t1==t4||t2==t4)
cout<<"YES"<<endl;
else
cout<<"NO"<<endl;
continue;
}
if(num1!=n1-2||num2!=n2-2){ //直角个数对不上
cout<<"NO"<<endl;
continue;
}
pair<int,int> U1 = v1[p1], V1 = v1[p2];
pair<int,int> U2 = v2[p3], V2 = v2[p4];
pair<int,int> U11 = v1[p11], V11 = v1[p22];
pair<int,int> U22 = v2[p33], V22 = v2[p44];
if((U1.first-V1.first)*(U1.first-V1.first)+(U1.second-V1.second)*(U1.second-V1.second)==(U2.first-V2.first)*(U2.first-V2.first)+(U2.second-V2.second)*(U2.second-V2.second)){
if(n1==4&&n2==4){ //分割为两四边形时还需要特判
//判两直角边相等
if((U11.first-V11.first)*(U11.first-V11.first)+(U11.second-V11.second)*(U11.second-V11.second)==(U22.first-V22.first)*(U22.first-V22.first)+(U22.second-V22.second)*(U22.second-V22.second))
cout<<"YES"<<endl;
else
cout<<"NO"<<endl;
}
else
cout<<"YES"<<endl;
}
else
cout<<"NO"<<endl;
}
}
L3-007 天梯地图
分数 60
全屏浏览
切换布局
作者 陈越
单位 浙江大学
本题要求你实现一个天梯赛专属在线地图,队员输入自己学校所在地和赛场地点后,该地图应该推荐两条路线:一条是最快到达路线;一条是最短距离的路线。题目保证对任意的查询请求,地图上都至少存在一条可达路线。
输入格式:
输入在第一行给出两个正整数N(2 ≤ N ≤ 500)和M,分别为地图中所有标记地点的个数和连接地点的道路条数。随后M行,每行按如下格式给出一条道路的信息:
V1 V2 one-way length time
其中V1和V2是道路的两个端点的编号(从0到N-1);如果该道路是从V1到V2的单行线,则one-way为1,否则为0;length是道路的长度;time是通过该路所需要的时间。最后给出一对起点和终点的编号。
输出格式:
首先按下列格式输出最快到达的时间T和用节点编号表示的路线:
Time = T: 起点 => 节点1 => ... => 终点
然后在下一行按下列格式输出最短距离D和用节点编号表示的路线:
Distance = D: 起点 => 节点1 => ... => 终点
如果最快到达路线不唯一,则输出几条最快路线中最短的那条,题目保证这条路线是唯一的。而如果最短距离的路线不唯一,则输出途径节点数最少的那条,题目保证这条路线是唯一的。
如果这两条路线是完全一样的,则按下列格式输出:
Time = T; Distance = D: 起点 => 节点1 => ... => 终点
输入样例1:
10 15
0 1 0 1 1
8 0 0 1 1
4 8 1 1 1
5 4 0 2 3
5 9 1 1 4
0 6 0 1 1
7 3 1 1 2
8 3 1 1 2
2 5 0 2 2
2 1 1 1 1
1 5 0 1 3
1 4 0 1 1
9 7 1 1 3
3 1 0 2 5
6 3 1 2 1
5 3
输出样例1:
Time = 6: 5 => 4 => 8 => 3
Distance = 3: 5 => 1 => 3
输入样例2:
7 9
0 4 1 1 1
1 6 1 3 1
2 6 1 1 1
2 5 1 2 2
3 0 0 1 1
3 1 1 3 1
3 2 1 2 1
4 5 0 2 2
6 5 1 2 1
3 5
输出样例2:
Time = 3; Distance = 4: 3 => 2 => 5//题目比较简单就是迪杰斯特拉算最短时间和最短路径,实际都差不多
#include <iostream>
#include<cstring>
#define inf 1<<30
using namespace std;
int m,n,source,destination;
int a,b,w,l,t;
int length[501][501],times[501][501];
int dis[501],cost[501],dis1[501],num[501],vis[501],path1[501],path2[501];
void getpath1(int x) {
if(x != source) {
getpath1(path1[x]);
printf(" => ");
}
printf("%d",x);
}
void getpath2(int x) {
if(x != source) {
getpath2(path2[x]);
printf(" => ");
}
printf("%d",x);
}
int equals(int x) {
if(path1[x] != path2[x])return 0;
else if(x == source)return 1;
return equals(path1[x]);
}
int main() {
cin>>n>>m;
for(int i = 0;i < n;i ++) {
for(int j = 0;j < n;j ++) {
length[i][j] = times[i][j] = inf;
}
dis[i] = cost[i] = dis1[i] = inf;
path1[i] = path2[i] = -1;
}
for(int i = 0;i < m;i ++) {
cin>>a>>b>>w>>l>>t;
if(w) {
length[a][b] = l;
times[a][b] = t;
}
else {
length[a][b] = length[b][a] = l;
times[a][b] = times[b][a] = t;
}
}
cin>>source>>destination;
dis[source] = cost[source] = dis1[source] = 0;
while(1) {
int t = -1,mi = inf;
//找最小
for(int i = 0;i < n;i ++) {
if(!vis[i] && mi > cost[i]) {
mi = cost[i];
t = i;
}
}
if(t == -1)
break;
vis[t] = 1;
for(int i = 0;i < n;i ++) {
if(vis[i] || times[t][i] == inf)
continue;
if(cost[i] > cost[t] + times[t][i]) {
path2[i] = t;
cost[i] = cost[t] + times[t][i];
dis1[i] = dis1[t] + length[t][i];
//dis1用来记录相同时间下的路径长度
}
else if(cost[i] == cost[t] + times[t][i] && dis1[i] > dis1[t] + length[t][i]) {
dis1[i] = dis1[t] + length[t][i];
path2[i] = t;
}
}
}
memset(vis,0,sizeof(vis));
while(1) {
int t = -1,mi = inf;
for(int i = 0;i < n;i ++) {
if(!vis[i] && mi > dis[i]) {
mi = dis[i];
t = i;
}
}
if(t == -1)break;
vis[t] = 1;
for(int i = 0;i < n;i ++) {
if(vis[i] || length[t][i] == inf)
continue;
if(dis[i] > dis[t] + length[t][i]) {
path1[i] = t;
dis[i] = dis[t] + length[t][i];
num[i] = num[t] + 1;
//num是节点个数
}
else if(dis[i] == dis[t] + length[t][i] && num[i] > num[t] + 1) {
num[i] = num[t] + 1;
path1[i] = t;
}
}
}
printf("Time = %d",cost[destination]);
if(!equals(destination)) {
printf(": ");
getpath2(destination);
printf("\n");
}
else {
printf("; ");
}
printf("Distance = %d: ",dis[destination]);
getpath1(destination);
}
L3-008 喊山
分数 60
全屏浏览
切换布局
作者 陈越
单位 浙江大学
喊山,是人双手围在嘴边成喇叭状,对着远方高山发出“喂—喂喂—喂喂喂……”的呼唤。呼唤声通过空气的传递,回荡于深谷之间,传送到人们耳中,发出约定俗成的“讯号”,达到声讯传递交流的目的。原来它是彝族先民用来求援呼救的“讯号”,慢慢地人们在生活实践中发现了它的实用价值,便把它作为一种交流工具世代传袭使用。(图文摘自:http://news.xrxxw.com/newsshow-8018.html)

一个山头呼喊的声音可以被临近的山头同时听到。题目假设每个山头最多有两个能听到它的临近山头。给定任意一个发出原始信号的山头,本题请你找出这个信号最远能传达到的地方。
输入格式:
输入第一行给出3个正整数n、m和k,其中n(≤10000)是总的山头数(于是假设每个山头从1到n编号)。接下来的m行,每行给出2个不超过n的正整数,数字间用空格分开,分别代表可以听到彼此的两个山头的编号。这里保证每一对山头只被输入一次,不会有重复的关系输入。最后一行给出k(≤10)个不超过n的正整数,数字间用空格分开,代表需要查询的山头的编号。
输出格式:
依次对于输入中的每个被查询的山头,在一行中输出其发出的呼喊能够连锁传达到的最远的那个山头。注意:被输出的首先必须是被查询的个山头能连锁传到的。若这样的山头不只一个,则输出编号最小的那个。若此山头的呼喊无法传到任何其他山头,则输出0。
输入样例:
7 5 4
1 2
2 3
3 1
4 5
5 6
1 4 5 7
输出样例:
2
6
4
0//题目挺常规的
//第一眼就是图深搜最深节点长度
//欧呦给坑了,这道题应该用bfs而不是dfs
#include<bits/stdc++.h>
using namespace std;
int n,m,k;
int vis[10001];
int sign[10001];
int level[10001];
int maxLevel=10001;
int minIndex;
vector<int> nodes[10001];
void bfs(int s){
queue<int>q;
q.push(s);
vis[s]=1;
while(!q.empty()){
int now=q.front();
q.pop();
for(int i=0;i<nodes[now].size();i++){
int nxt=nodes[now][i];
if(vis[nxt])
continue;
q.push(nxt);
vis[nxt]=1;
level[nxt]=level[now]+1;
if(level[nxt]>maxLevel){
maxLevel=level[nxt];
minIndex=nxt;
}else if(level[nxt]==maxLevel){
if(minIndex>nxt){
minIndex=nxt;
}
}
}
}
}
int main(){
cin>>n>>m>>k;
for(int i=1;i<=m;i++){
int a,b;
cin>>a>>b;
nodes[a].push_back(b);
nodes[b].push_back(a);
sign[a]=sign[b]=1;
}
for(int i=0;i<k;i++){
int s;
cin>>s;
maxLevel=-1;
minIndex=10001;
for(int j=1;j<=n;j++){
vis[j]=0;
}
for(int j=1;j<=n;j++){
level[j]=0;
}
if(0==sign[s]){
cout<<"0"<<endl;
continue;
}
bfs(s);
cout<<minIndex<<endl;
}
}
L3-009 长城
分数 80
全屏浏览
切换布局
作者 邓俊辉
单位 清华大学
正如我们所知,中国古代长城的建造是为了抵御外敌入侵。在长城上,建造了许多烽火台。每个烽火台都监视着一个特定的地区范围。一旦某个地区有外敌入侵,值守在对应烽火台上的士兵就会将敌情通报给周围的烽火台,并迅速接力地传递到总部。
现在如图1所示,若水平为南北方向、垂直为海拔高度方向,假设长城就是依次相联的一系列线段,而且在此范围内的任一垂直线与这些线段有且仅有唯一的交点。
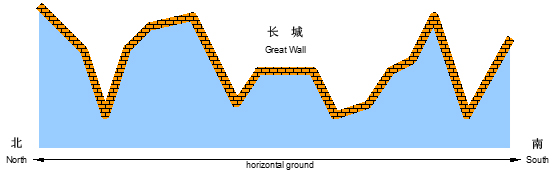
图 1
进一步地,假设烽火台只能建造在线段的端点处。我们认为烽火台本身是没有高度的,每个烽火台只负责向北方(图1中向左)瞭望,而且一旦有外敌入侵,只要敌人与烽火台之间未被山体遮挡,哨兵就会立即察觉。当然,按照这一军规,对于南侧的敌情各烽火台并不负责任。一旦哨兵发现敌情,他就会立即以狼烟或烽火的形式,向其南方的烽火台传递警报,直到位于最南侧的总部。
以图2中的长城为例,负责守卫的四个烽火台用蓝白圆点示意,最南侧的总部用红色圆点示意。如果红色星形标示的地方出现敌情,将被哨兵们发现并沿红色折线将警报传递到总部。当然,就这个例子而言只需两个烽火台的协作,但其他位置的敌情可能需要更多。
然而反过来,即便这里的4个烽火台全部参与,依然有不能覆盖的(黄色)区域。
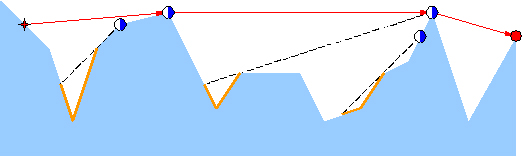
图 2
另外,为避免歧义,我们在这里约定,与某个烽火台的视线刚好相切的区域都认为可以被该烽火台所监视。以图3中的长城为例,若A、B、C、D点均共线,且在D点设置一处烽火台,则A、B、C以及线段BC上的任何一点都在该烽火台的监视范围之内。
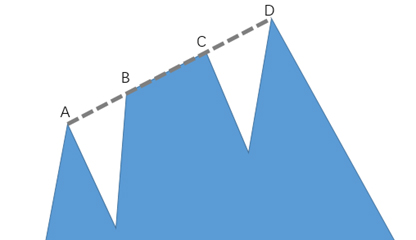
图 3
好了,倘若你是秦始皇的太尉,为不致出现更多孟姜女式的悲剧,如何在保证长城安全的前提下,使消耗的民力(建造的烽火台)最少呢?
输入格式:
输入在第一行给出一个正整数N(3 ≤ N ≤105),即刻画长城边缘的折线顶点(含起点和终点)数。随后N行,每行给出一个顶点的x和y坐标,其间以空格分隔。注意顶点从南到北依次给出,第一个顶点为总部所在位置。坐标为区间[−109,109)内的整数,且没有重合点。
输出格式:
在一行中输出所需建造烽火台(不含总部)的最少数目。
输入样例:
10
67 32
48 -49
32 53
22 -44
19 22
11 40
10 -65
-1 -23
-3 31
-7 59
输出样例:
2//看题目那么长实际上就两句话
//1.从右往左一次给出点的位置
//2.求最少的点数,两点之间可以覆盖所有的点
//假设当前点为A,他的右边有相邻点B,C,此时若是AC*AB<0,即AB在AC上方,此时B为凸点。
//做题的时候把从右到做的点依次入栈,每次判断栈顶的点是否会成为凸点(AB在AC上方),不会就丢掉,直到遇到会的
//注意一下数据范围是要用long long
#include<iostream>
#include<set>
using namespace std;
long long x[100000];
long long y[100000];
long long stack[1000000];//充当栈
bool check(int a,int b,int c){
return (x[c]-x[a])*(y[b]-y[a])<=(x[b]-x[a])*(y[c]-y[a]);//就是比较斜率
}
int main(){
int n;
cin>>n;
int count=0;
set<int> s;
for(int i=0;i<n;i++){
cin>>x[i]>>y[i];
if(count>=1){
while(count>=2&&check(i,stack[count-1],stack[count-2])){
count--;
}
if(stack[count-1])
s.insert(stack[count-1]);//set为了避免重复
}
stack[count++]=i;
}
cout<<s.size()<<endl;
}
L3-010 是否完全二叉搜索树
分数 60
全屏浏览
切换布局
作者 陈越
单位 浙江大学
将一系列给定数字顺序插入一个初始为空的二叉搜索树(定义为左子树键值大,右子树键值小),你需要判断最后的树是否一棵完全二叉树,并且给出其层序遍历的结果。
输入格式:
输入第一行给出一个不超过20的正整数N;第二行给出N个互不相同的正整数,其间以空格分隔。
输出格式:
将输入的N个正整数顺序插入一个初始为空的二叉搜索树。在第一行中输出结果树的层序遍历结果,数字间以1个空格分隔,行的首尾不得有多余空格。第二行输出YES,如果该树是完全二叉树;否则输出NO。
输入样例1:
9
38 45 42 24 58 30 67 12 51
输出样例1:
38 45 24 58 42 30 12 67 51
YES
输入样例2:
8
38 24 12 45 58 67 42 51
输出样例2:
38 45 24 58 42 12 67 51
NO//题目挺常规的,设个数组直接建树就好了
#include<iostream>
using namespace std;
int shu[300]={0};
void insert(int x, int index){
if(shu[index]==0){
shu[index]=x;
return ;
}
if(x>shu[index]){
insert(x,index*2);
}
else{
insert(x,index*2+1);
}
}
int main(){
int n;
cin>>n;
for(int i=0;i<n;i++){
int x;
cin>>x;
insert(x,1);
}
int flag=1;
for(int i=1;i<=n;i++){
if(shu[i]==0){
flag=0;
break;
}
}
cout<<shu[1];//因为第一个节点是必定有直的
for(int i=2;i<=299;i++){
if(shu[i]!=0){
cout<<" "<<shu[i];
}
}
cout<<endl;
if(flag==0)
cout<<"NO";
else
cout<<"YES";
}
L3-011 直捣黄龙
分数 60
全屏浏览
切换布局
作者 陈越
单位 浙江大学
本题是一部战争大片 —— 你需要从己方大本营出发,一路攻城略地杀到敌方大本营。首先时间就是生命,所以你必须选择合适的路径,以最快的速度占领敌方大本营。当这样的路径不唯一时,要求选择可以沿途解放最多城镇的路径。若这样的路径也不唯一,则选择可以有效杀伤最多敌军的路径。
输入格式:
输入第一行给出2个正整数N(2 ≤ N ≤ 200,城镇总数)和K(城镇间道路条数),以及己方大本营和敌方大本营的代号。随后N-1行,每行给出除了己方大本营外的一个城镇的代号和驻守的敌军数量,其间以空格分隔。再后面有K行,每行按格式城镇1 城镇2 距离给出两个城镇之间道路的长度。这里设每个城镇(包括双方大本营)的代号是由3个大写英文字母组成的字符串。
输出格式:
按照题目要求找到最合适的进攻路径(题目保证速度最快、解放最多、杀伤最强的路径是唯一的),并在第一行按照格式己方大本营->城镇1->...->敌方大本营输出。第二行顺序输出最快进攻路径的条数、最短进攻距离、歼敌总数,其间以1个空格分隔,行首尾不得有多余空格。
输入样例:
10 12 PAT DBY
DBY 100
PTA 20
PDS 90
PMS 40
TAP 50
ATP 200
LNN 80
LAO 30
LON 70
PAT PTA 10
PAT PMS 10
PAT ATP 20
PAT LNN 10
LNN LAO 10
LAO LON 10
LON DBY 10
PMS TAP 10
TAP DBY 10
DBY PDS 10
PDS PTA 10
DBY ATP 10
输出样例:
PAT->PTA->PDS->DBY
3 30 210//怎么说呢,题目不难,简单点来说就是迪杰斯特拉算法
//我们默认将己方大本营当做节点0
#include<iostream>
#include<map>
#include<vector>
#define INF 1e9
using namespace std;
int N,K;
map<string,int> daihao;
map<int,string> daihao2;
map<string,int> renshu;
int g[200][200];
int dist[200];//距离
int parent[200];//父母
int num[200];//节点个数也就是解放城镇数量
int shadi[200];
int visit[200];
int path[200];//路的数量
void init(){
for(int i=0;i<N;i++){
dist[i]=INF;
}
for(int i=0;i<N;i++){
for(int j=0;j<N;j++){
g[i][j]=INF;
}
}
}
int findmind(){
int min=INF;
int index;
int flag=0;
for(int i=1;i<N;i++){
if(visit[i]==0&&dist[i]<min){
min=dist[i];
index=i;
flag=1;
}
}
if(flag==1)
return index;
else
return -1;
}
void dij(){
visit[0]=1;
path[0]=1;
dist[0]=0;
for(int i=0;i<N;i++){
if(g[0][i]!=INF){
dist[i]=g[0][i];
path[i]=1;
shadi[i]=renshu[daihao2[i]];
}
}
while(findmind()!=-1){
int x=findmind();
visit[x]=1;
for(int i=0;i<N;i++){
if(visit[i]==0&&dist[i]>dist[x]+g[x][i]){
dist[i]=dist[x]+g[x][i];
parent[i]=x;
shadi[i]=shadi[x]+renshu[daihao2[i]];
num[i]=num[x]+1;
path[i]=path[x];
}
else if(visit[i]==0&&dist[i]==dist[x]+g[x][i]){
path[i]=path[x]+path[i];
if(num[i]<num[x]+1){
parent[i]=x;
shadi[i]=shadi[x]+renshu[daihao2[i]];
num[i]=num[x]+1;
}
else if(num[i]==num[x]+1){
if(shadi[i]<shadi[x]+renshu[daihao2[i]]){
parent[i]=x;
shadi[i]=shadi[x]+renshu[daihao2[i]];
}
}
}
}
}
}
int main(){
cin>>N>>K;
string a1,a2;
cin>>a1>>a2;
daihao[a1]=0;
renshu[a1]=0;//自己家守军人数当0
init();
for(int i=1;i<N;i++){
string x;
int y;
cin>>x>>y;
daihao[x]=i;
daihao2[i]=x;
renshu[x]=y;
}
for(int i=0;i<K;i++){
string a1,a2;
int x;
cin>>a1>>a2>>x;
g[daihao[a1]][daihao[a2]]=x;
g[daihao[a2]][daihao[a1]]=x;
}
dij();
cout<<a1;
vector<string> v;
int t=daihao[a2];
while(t!=0){
v.push_back(daihao2[t]);
t=parent[t];
}
for(int i=0;i<v.size();i++){
cout<<"->"<<v[v.size()-i-1];
}
cout<<endl;
cout<<path[daihao[a2]]<<" "<<dist[daihao[a2]]<<" "<<shadi[daihao[a2]];
}
L3-012 水果忍者
分数 80
全屏浏览
切换布局
作者 邓俊辉、罗必成
单位 清华大学
2010年风靡全球的“水果忍者”游戏,想必大家肯定都玩过吧?(没玩过也没关系啦~)在游戏当中,画面里会随机地弹射出一系列的水果与炸弹,玩家尽可能砍掉所有的水果而避免砍中炸弹,就可以完成游戏规定的任务。如果玩家可以一刀砍下画面当中一连串的水果,则会有额外的奖励,如图1所示。

图 1
现在假如你是“水果忍者”游戏的玩家,你要做的一件事情就是,将画面当中的水果一刀砍下。这个问题看上去有些复杂,让我们把问题简化一些。我们将游戏世界想象成一个二维的平面。游戏当中的每个水果被简化成一条一条的垂直于水平线的竖直线段。而一刀砍下我们也仅考虑成能否找到一条直线,使之可以穿过所有代表水果的线段。
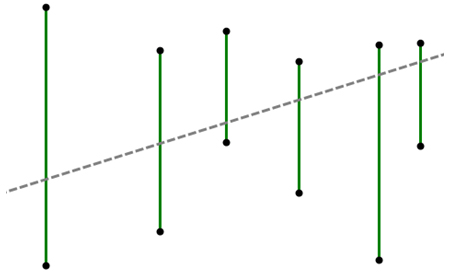
图 2
如图2所示,其中绿色的垂直线段表示的就是一个一个的水果;灰色的虚线即表示穿过所有线段的某一条直线。可以从上图当中看出,对于这样一组线段的排列,我们是可以找到一刀切开所有水果的方案的。
另外,我们约定,如果某条直线恰好穿过了线段的端点也表示它砍中了这个线段所表示的水果。假如你是这样一个功能的开发者,你要如何来找到一条穿过它们的直线呢?
输入格式:
输入在第一行给出一个正整数N(≤104),表示水果的个数。随后N行,每行给出三个整数x、y1、y2,其间以空格分隔,表示一条端点为(x,y1)和(x,y2)的水果,其中y1>y2。注意:给出的水果输入集合一定存在一条可以将其全部穿过的直线,不需考虑不存在的情况。坐标为区间 [−106,106) 内的整数。
输出格式:
在一行中输出穿过所有线段的直线上具有整数坐标的任意两点p1(x1,y1)和p2(x2,y2),格式为 x1y1x2y2。注意:本题答案不唯一,由特殊裁判程序判定,但一定存在四个坐标全是整数的解。
输入样例:
5
-30 -52 -84
38 22 -49
-99 -22 -99
48 59 -18
-36 -50 -72
输出样例:
-99 -99 -30 -52//这道题思路不难
//额由于他是一个范围嘛,那么我们直接找边界点
//只要找出一条线的边界点可以通过所有线就行了
//主要的思路就是不断缩小大斜率和小斜率的范围即可
#include<iostream>
#include<vector>
#include<algorithm>
using namespace std;
struct Line {
double x, y1, y2;
};
bool cmp(const Line &lhs, const Line &rhs) {
return lhs.x < rhs.x;
}
int main() {
int n;
cin >> n;
vector<Line> lines(n);
for (int i = 0; i < n; ++i) {
cin >> lines[i].x >> lines[i].y1 >> lines[i].y2;
}
//最开始没想到对x进行排序,所以在判断在线的左右时会出错所以还是排序一下,或者可以自己判断一下
sort(lines.begin(),lines.end(),cmp);
for (int i = 0; i < n; i++) {
double Max= 1e9;
double Min = -1e9;
bool isMinSlope = false;//这个实际上是用来判断最后一条线到底是上点还是下点
Line ansLine;
int j = 0;
for (j=0; j < n; j++) {
if (i == j) continue;
double minSlope, maxSlope;
//在线的左边时,上端点为小,下端点为大,反之亦然
if (i < j) {
maxSlope = (lines[i].y2 - lines[j].y1) / (lines[i].x - lines[j].x);
minSlope = (lines[i].y2 - lines[j].y2) / (lines[i].x - lines[j].x);
} else {
maxSlope = (lines[i].y2 - lines[j].y2) / (lines[i].x - lines[j].x);
minSlope = (lines[i].y2 - lines[j].y1) / (lines[i].x - lines[j].x);
}
//炸喽
if (maxSlope < Min || minSlope > Max)
break;
// 更新最大最小斜率
if (maxSlope < Max) {
Max = maxSlope;
ansLine = lines[j];
isMinSlope = false;
}
if (minSlope > Min) {
Min = minSlope;
ansLine = lines[j];
isMinSlope = true;
}
}
// 如果直到最后一条线段都能满足,就说明所有线段都能满足
if (j == n) {
printf("%.0f %.0f %.0f %.0f", lines[i].x, lines[i].y2, ansLine.x, (isMinSlope ? ansLine.y2 : ansLine.y1));
return 0;
}
}
return 0;
}
L3-013 非常弹的球
分数 60
全屏浏览
切换布局
作者 俞勇
单位 上海交通大学
刚上高一的森森为了学好物理,买了一个“非常弹”的球。虽然说是非常弹的球,其实也就是一般的弹力球而已。森森玩了一会儿弹力球后突然想到,假如他在地上用力弹球,球最远能弹到多远去呢?他不太会,你能帮他解决吗?当然为了刚学习物理的森森,我们对环境做一些简化:
- 假设森森是一个质点,以森森为原点设立坐标轴,则森森位于(0, 0)点。
- 小球质量为w/100 千克(kg),重力加速度为9.8米/秒平方(m/s2)。
- 森森在地上用力弹球的过程可简化为球从(0, 0)点以某个森森选择的角度ang (0<ang<π/2) 向第一象限抛出,抛出时假设动能为1000 焦耳(J)。
- 小球在空中仅受重力作用,球纵坐标为0时可视作落地,落地时损失p%动能并反弹。
- 地面可视为刚体,忽略小球形状、空气阻力及摩擦阻力等。
森森为你准备的公式:
- 动能公式:E=m×v2/2
- 牛顿力学公式:F=m×a
- 重力:G=m×g
其中:
- E - 动能,单位为“焦耳”
- m - 质量,单位为“千克”
- v - 速度,单位为“米/秒”
- a - 加速度,单位为“米/秒平方”
- g - 重力加速度
输入格式:
输入在一行中给出两个整数:1≤w≤1000 和 1≤p≤100,分别表示放大100倍的小球质量、以及损失动力的百分比p。
输出格式:
在一行输出最远的投掷距离,保留3位小数。
输入样例:
100 90
输出样例:
226.757//这道题目趋向于无限啊
//主要是确定动能足够小就好
#include<iostream>
#include<cmath>
using namespace std;
int main(){
double m,p;
double E=1000;
double g=9.8;
double h,t,v;
cin>>m>>p;
p=1-p/100;//比例
m/=100;
double ans=0;
while(E>1e-9){
h=E/(2*m*g);
t=sqrt(2*h/g);
v=sqrt(E/m);
ans+=2*v*t;
E*=p;
}
printf("%.3f\n",ans);
}
L3-014 周游世界
分数 60
全屏浏览
切换布局
作者 陈越
单位 浙江大学
周游世界是件浪漫事,但规划旅行路线就不一定了…… 全世界有成千上万条航线、铁路线、大巴线,令人眼花缭乱。所以旅行社会选择部分运输公司组成联盟,每家公司提供一条线路,然后帮助客户规划由联盟内企业支持的旅行路线。本题就要求你帮旅行社实现一个自动规划路线的程序,使得对任何给定的起点和终点,可以找出最顺畅的路线。所谓“最顺畅”,首先是指中途经停站最少;如果经停站一样多,则取需要换乘线路次数最少的路线。
输入格式:
输入在第一行给出一个正整数N(≤100),即联盟公司的数量。接下来有N行,第i行(i=1,⋯,N)描述了第i家公司所提供的线路。格式为:
M S[1] S[2] ⋯ S[M]
其中M(≤100)是经停站的数量,S[i](i=1,⋯,M)是经停站的编号(由4位0-9的数字组成)。这里假设每条线路都是简单的一条可以双向运行的链路,并且输入保证是按照正确的经停顺序给出的 —— 也就是说,任意一对相邻的S[i]和S[i+1](i=1,⋯,M−1)之间都不存在其他经停站点。我们称相邻站点之间的线路为一个运营区间,每个运营区间只承包给一家公司。环线是有可能存在的,但不会不经停任何中间站点就从出发地回到出发地。当然,不同公司的线路是可能在某些站点有交叉的,这些站点就是客户的换乘点,我们假设任意换乘点涉及的不同公司的线路都不超过5条。
在描述了联盟线路之后,题目将给出一个正整数K(≤10),随后K行,每行给出一位客户的需求,即始发地的编号和目的地的编号,中间以一空格分隔。
输出格式:
处理每一位客户的需求。如果没有现成的线路可以使其到达目的地,就在一行中输出“Sorry, no line is available.”;如果目的地可达,则首先在一行中输出最顺畅路线的经停站数量(始发地和目的地不包括在内),然后按下列格式给出旅行路线:
Go by the line of company #X1 from S1 to S2.
Go by the line of company #X2 from S2 to S3.
......
其中Xi是线路承包公司的编号,Si是经停站的编号。但必须只输出始发地、换乘点和目的地,不能输出中间的经停站。题目保证满足要求的路线是唯一的。
输入样例:
4
7 1001 3212 1003 1204 1005 1306 7797
9 9988 2333 1204 2006 2005 2004 2003 2302 2001
13 3011 3812 3013 3001 1306 3003 2333 3066 3212 3008 2302 3010 3011
4 6666 8432 4011 1306
4
3011 3013
6666 2001
2004 3001
2222 6666
输出样例:
2
Go by the line of company #3 from 3011 to 3013.
10
Go by the line of company #4 from 6666 to 1306.
Go by the line of company #3 from 1306 to 2302.
Go by the line of company #2 from 2302 to 2001.
6
Go by the line of company #2 from 2004 to 1204.
Go by the line of company #1 from 1204 to 1306.
Go by the line of company #3 from 1306 to 3001.
Sorry, no line is available.//额题目不难就是深搜最短路径就行了,然后就是额记录一下具体路径
#include<bits/stdc++.h>
using namespace std;
const int maxn = 10010;
const int maxe = 100010;
int minCnt, minTrans;
vector<int> path, tempath;
int line[maxn][maxn]; //维护两点之间的线路归属
int head[maxn], nxt[maxe], to[maxe], edgeLine[maxe]; //链式向前星相关数组
int edgeCount = 0;
int count(vector<int> a) { //给出路径,计算换乘
int cnt = -1, preLine = 0;
for(int i = 1; i < a.size(); i++) {
if(line[a[i-1]][a[i]] != preLine) cnt++;
preLine = line[a[i-1]][a[i]];
}
return cnt;
}
int vis[maxn];
void dfs(int u, int end, int cnt) {
if(u == end) {
if(cnt < minCnt || (cnt == minCnt && count(tempath) < minTrans)) {
minCnt = cnt;
minTrans = count(tempath);
path = tempath;
}
return;
}
for(int i = head[u]; i != -1; i = nxt[i]) {
int v = to[i];
if(!vis[v]) {
vis[v] = 1;
tempath.push_back(v);
dfs(v, end, cnt + 1);
vis[v] = 0;
tempath.pop_back();
}
}
}
void addEdge(int u, int v, int l) {
to[edgeCount] = v;
nxt[edgeCount] = head[u];
edgeLine[edgeCount] = l;
head[u] = edgeCount++;
}
int main() {
int n, m, k, pre, tmp, a, b;
memset(head, -1, sizeof(head)); // 初始化head数组
cin >> n;
for(int i = 1; i <= n; i++) {
cin >> m >> pre;
for(int j = 2; j <= m; j++) {
cin >> tmp;
addEdge(pre, tmp, i);
addEdge(tmp, pre, i);
line[pre][tmp] = i;
line[tmp][pre] = i;
pre = tmp;
}
}
cin >> k;
for(int i = 1; i <= k; i++) {
cin >> a >> b;
minCnt = 1e9, minTrans = 1e9;
tempath.clear();
tempath.push_back(a);
memset(vis, 0, sizeof(vis)); // 清除vis数组
vis[a] = 1;
dfs(a, b, 0);
vis[a] = 0;
if(minCnt == 1e9) {
printf("Sorry, no line is available.\n");
continue;
}
cout << minCnt << "\n";
int preLine = 0, preTrans = a; //上次的线路,以及转乘点
for(int j = 1; j < path.size(); j++) {
if(line[path[j-1]][path[j]] != preLine) {
if(preLine != 0) printf("Go by the line of company #%d from %04d to %04d.\n", preLine, preTrans, path[j-1]);
preLine = line[path[j-1]][path[j]];
preTrans = path[j-1];
}
}
printf("Go by the line of company #%d from %04d to %04d.\n", preLine, preTrans, b);
}
return 0;
}
L3-015 球队“食物链”
分数 80
全屏浏览
切换布局
作者 李文新
单位 北京大学
某国的足球联赛中有N支参赛球队,编号从1至N。联赛采用主客场双循环赛制,参赛球队两两之间在双方主场各赛一场。
联赛战罢,结果已经尘埃落定。此时,联赛主席突发奇想,希望从中找出一条包含所有球队的“食物链”,来说明联赛的精彩程度。“食物链”为一个1至N的排列{ T1 T2 ⋯ TN },满足:球队T1战胜过球队T2,球队T2战胜过球队T3,⋯,球队T(N−1)战胜过球队TN,球队TN战胜过球队T1。
现在主席请你从联赛结果中找出“食物链”。若存在多条“食物链”,请找出字典序最小的。
注:排列{ a1 a2 ⋯ aN}在字典序上小于排列{ b1 b2 ⋯ bN },当且仅当存在整数K(1≤K≤N),满足:aK<bK且对于任意小于K的正整数i,ai=bi。
输入格式:
输入第一行给出一个整数N(2≤N≤20),为参赛球队数。随后N行,每行N个字符,给出了N×N的联赛结果表,其中第i行第j列的字符为球队i在主场对阵球队j的比赛结果:W表示球队i战胜球队j,L表示球队i负于球队j,D表示两队打平,-表示无效(当i=j时)。输入中无多余空格。
输出格式:
按题目要求找到“食物链”T1 T2 ⋯ TN,将这N个数依次输出在一行上,数字间以1个空格分隔,行的首尾不得有多余空格。若不存在“食物链”,输出“No Solution”。
输入样例1:
5
-LWDW
W-LDW
WW-LW
DWW-W
DDLW-
输出样例1:
1 3 5 4 2
输入样例2:
5
-WDDW
D-DWL
DD-DW
DDW-D
DDDD-
输出样例2:
No Solution//题目感觉不难,数据也挺小的,额如果换成图就直接邻接矩阵就好了
//大概的思路就是深搜
//我靠怎么会爆炸啊
//我看看怎么回事
//哦我知道了,要剪枝,如果说剩下的队伍里面没有能够干死第一支队伍的那就没必要继续比较了
//好这样就过了
#include<bits/stdc++.h>
using namespace std;
const int N=22;
int g[N][N];
int st[N];//是否访问
bool flag;
int n;
int xulie[N];//xulie用来储存球队顺序
//u是从哪个球队开始,index是第几支球队,每次递归记得加1
void dfs(int u,int index){
//直接返回1
if(flag)
return;
//这里没必要管啊,因为回溯会自动覆盖的
xulie[index]=u;
//这里仔细看题目,要首尾成一个环我没仔细看
//这种情况是完全成立
if(index==n&&g[u][1]){
flag=1;
return;
}
//这种情况只是满足了前面的情况没打过第一支队伍
if(index==n)
return;
//剪枝
bool fl=0;
for(int i=1;i<=n;i++){
if(!st[i]&&g[i][1])
fl=1;
}
if(!fl)
return;
//从1开始深搜
st[u]=1;
for(int i=1;i<=n;i++){
if(!st[i]&&g[u][i]){
st[u]=1;
dfs(i,index+1);
}
}
//回溯
st[u]=0;
}
int main(){
cin>>n;
for(int i=1;i<=n;i++){
for(int j=1;j<=n;j++){
char c;
cin>>c;
//额这个图是个单向图啊,别写成双向了
if(c=='W')
g[i][j]=1;
if(c=='L')
g[j][i]=1;
}
}
st[1]=1;
dfs(1,1);
if(!flag)
puts("No Solution");
else {
for(int i=1;i<n;i++)
cout<<xulie[i]<<" ";
cout<<xulie[n]<<endl;
}
}
L3-016 二叉搜索树的结构
分数 60
全屏浏览
切换布局
作者 陈越
单位 浙江大学
二叉搜索树或者是一棵空树,或者是具有下列性质的二叉树: 若它的左子树不空,则左子树上所有结点的值均小于它的根结点的值;若它的右子树不空,则右子树上所有结点的值均大于它的根结点的值;它的左、右子树也分别为二叉搜索树。(摘自百度百科)
给定一系列互不相等的整数,将它们顺次插入一棵初始为空的二叉搜索树,然后对结果树的结构进行描述。你需要能判断给定的描述是否正确。例如将{ 2 4 1 3 0 }插入后,得到一棵二叉搜索树,则陈述句如“2是树的根”、“1和4是兄弟结点”、“3和0在同一层上”(指自顶向下的深度相同)、“2是4的双亲结点”、“3是4的左孩子”都是正确的;而“4是2的左孩子”、“1和3是兄弟结点”都是不正确的。
输入格式:
输入在第一行给出一个正整数N(≤100),随后一行给出N个互不相同的整数,数字间以空格分隔,要求将之顺次插入一棵初始为空的二叉搜索树。之后给出一个正整数M(≤100),随后M行,每行给出一句待判断的陈述句。陈述句有以下6种:
A is the root,即"A是树的根";A and B are siblings,即"A和B是兄弟结点";A is the parent of B,即"A是B的双亲结点";A is the left child of B,即"A是B的左孩子";A is the right child of B,即"A是B的右孩子";A and B are on the same level,即"A和B在同一层上"。
题目保证所有给定的整数都在整型范围内。
输出格式:
对每句陈述,如果正确则输出Yes,否则输出No,每句占一行。
输入样例:
5
2 4 1 3 0
8
2 is the root
1 and 4 are siblings
3 and 0 are on the same level
2 is the parent of 4
3 is the left child of 4
1 is the right child of 2
4 and 0 are on the same level
100 is the right child of 3
输出样例:
Yes
Yes
Yes
Yes
Yes
No
No
No//首先呢这道题并不是很难
//直接数组构建二叉树就行了
#include<bits/stdc++.h>
using namespace std;
map<int,int> mp;
const int N = 10000;
int T, n, m;
int a[N];
struct node{
int x, left, right;
int flor;
int fa;
}node[N];
int cnt;
void dfs(int x, int u){
if(x < node[u].x){
if(!node[u].left){
cnt++;
node[cnt].x = x;
node[u].left = cnt;
node[cnt].fa = u;
node[cnt].flor = node[u].flor + 1;
mp[x] = cnt;
}
else{
dfs(x, node[u].left);
}
}
else{
if(!node[u].right){
cnt++;
node[cnt].x = x;
node[u].right = cnt;
node[cnt].fa = u;
node[cnt].flor = node[u].flor + 1;
mp[x] = cnt;
}
else{
dfs(x, node[u].right);
}
}
}
int main(){
cin>>n;
int x;
cin>>x;
node[1].x = x;
node[1].flor = 1;
mp[x] = 1;
cnt = 1;
for(int i=2;i<=n;i++){
cin>>x;
dfs(x, 1);
}
cin>>m;
string s;
getchar();
while(m--){
getline(cin, s);
int x = 0;
int y = 0;
if(s.find("root") != s.npos){
sscanf(s.c_str(), "%d is the root", &x);
if(mp[x] == 1) cout<<"Yes\n";
else
cout<<"No\n";
}
if(s.find("siblings") != s.npos){
sscanf(s.c_str(), "%d and %d are siblings", &x, &y);
x = mp[x];
y = mp[y];
if(!x || !y)
cout<<"No\n"; //需要先判断该值是否在树中
else if(node[x].fa != node[y].fa)
cout<<"No\n";
else
cout<<"Yes\n";
}
if(s.find("parent") != s.npos){
sscanf(s.c_str(), "%d is the parent of %d", &x, &y);
x = mp[x];
y = mp[y];
if(!x || !y)
cout<<"No\n";
else if(node[y].fa == x)
cout<<"Yes\n";
else
cout<<"No\n";
}
if(s.find("left") != s.npos){
sscanf(s.c_str(), "%d is the left child of %d", &x, &y);
x = mp[x];
y = mp[y];
if(!x || !y)
cout<<"No\n";
else if(node[y].left == x)
cout<<"Yes\n";
else
cout<<"No\n";
}
if(s.find("right") != s.npos){
sscanf(s.c_str(), "%d is the right child of %d", &x, &y);
x = mp[x];
y = mp[y];
if(!x || !y)
cout<<"No\n";
else if(node[y].right == x)
cout<<"Yes\n";
else
cout<<"No\n";
}
if(s.find("level") != s.npos){
sscanf(s.c_str(), "%d and %d are on the same level", &x, &y);
x = mp[x];
y = mp[y];
if(!x || !y)
cout<<"No\n";
else if(node[y].flor == node[x].flor)
cout<<"Yes\n";
else
cout<<"No\n";
}
}
}
L3-017 森森快递
分数 60
全屏浏览
切换布局
作者 俞勇
单位 上海交通大学
森森开了一家快递公司,叫森森快递。因为公司刚刚开张,所以业务路线很简单,可以认为是一条直线上的N个城市,这些城市从左到右依次从0到(N−1)编号。由于道路限制,第i号城市(i=0,⋯,N−2)与第(i+1)号城市中间往返的运输货物重量在同一时刻不能超过Ci公斤。
公司开张后很快接到了Q张订单,其中j张订单描述了某些指定的货物要从Sj号城市运输到Tj号城市。这里我们简单地假设所有货物都有无限货源,森森会不定时地挑选其中一部分货物进行运输。安全起见,这些货物不会在中途卸货。
为了让公司整体效益更佳,森森想知道如何安排订单的运输,能使得运输的货物重量最大且符合道路的限制?要注意的是,发货时间有可能是任何时刻,所以我们安排订单的时候,必须保证共用同一条道路的所有货车的总重量不超载。例如我们安排1号城市到4号城市以及2号城市到4号城市两张订单的运输,则这两张订单的运输同时受2-3以及3-4两条道路的限制,因为两张订单的货物可能会同时在这些道路上运输。
输入格式:
输入在第一行给出两个正整数N和Q(2≤N≤105, 1≤Q≤105),表示总共的城市数以及订单数量。
第二行给出(N−1)个数,顺次表示相邻两城市间的道路允许的最大运货重量Ci(i=0,⋯,N−2)。题目保证每个Ci是不超过231的非负整数。
接下来Q行,每行给出一张订单的起始及终止运输城市编号。题目保证所有编号合法,并且不存在起点和终点重合的情况。
输出格式:
在一行中输出可运输货物的最大重量。
输入样例:
10 6
0 7 8 5 2 3 1 9 10
0 9
1 8
2 7
6 3
4 5
4 2
输出样例:
7
样例提示:我们选择执行最后两张订单,即把5公斤货从城市4运到城市2,并且把2公斤货从城市4运到城市5,就可以得到最大运输量7公斤。
//构思了一个小时才大概想好
//这道题简单点来说就是在一段线路上找最大运输量,且运输的时候不能超过每条路的负载
//那么我们在一段路上的最大运输量很显然要小于等于这段路的最小负载
//额简单点来说就是列如我1到2是3的负载,2到3是7的负载,那你想要1到3是不是最多只能运3
//那这样就比较简单了,实际上这就是一个区间贪心加上一个线段树维护最小值
//至于为什么是线段树,额其实就是这是一个区间的最小值嘛很显然用线段树会比较好
//注意每选择一个订单就要更新线段树的最小值(注意这里是区间修改,区间查询)
//巐段错误了,发现中间有个数组下标写错了,额注意最后minn一定要定大一点不然最后一个测试点过不了
#include<iostream>
#include<algorithm>
using namespace std;
typedef long long ll;//这里注意数据大小有2的31次所以采用longlong
const int maxn=2e5 + 10;
//这边线段树不会的自己去看就不多说了
typedef struct node{
int l,r;
ll minn;
ll lazy;
//这里我们按照额右端点为第一关键字升序,左端点为第二关键字降序
//简单点来讲就是终点越接近左边就越容易流出更多的空间给后面的订单
bool operator < (const node x) const {
if(x.r != r)
return x.r > r;
else
return x.l < l;
}
}node;
node tree[maxn<<2];
node ans[maxn]; //数字过大建议采用二进制计算,这个是订单
ll minn;
//建树
void build(int k, int l, int r){
tree[k].l=l,tree[k].r=r;
if(l==r){
cin>>tree[k].minn;
return;
}
int mid=(l+r)>>1;
build(k<<1,l,mid);
build(k<<1|1,mid+1,r);
tree[k].minn = min(tree[k<<1].minn, tree[k<<1|1].minn);
}
//lazy下沉
void down(int k){
if(tree[k].lazy){
tree[k<<1].lazy+=tree[k].lazy;
tree[k<<1|1].lazy+=tree[k].lazy;
tree[k<<1].minn-=tree[k].lazy;
tree[k<<1|1].minn-=tree[k].lazy;
tree[k].lazy = 0;
}
}
//修改
void add(int i,int l,int r,int k){
if(tree[i].l>=l&&tree[i].r<=r){
tree[i].lazy+=k;
tree[i].minn-=k;
return;
}
down(i);
int mid=(tree[i].l+tree[i].r)>>1;
if(l<=mid)
add(i<<1,l,r,k);
if(r>mid)
add(i<<1|1,l,r,k);
tree[i].minn=min(tree[i<<1].minn,tree[i<<1|1].minn);
}
//区间查询
void query(int i, int l, int r){
if(tree[i].l>=l && tree[i].r<=r){
minn=min(minn,tree[i].minn);
return;
}
down(i);
int mid = (tree[i].l+tree[i].r)>>1;
if(l<=mid)
query(i<<1,l,r);
if(r>mid)
query(i<<1|1,l,r);
}
int n,q;
int main(){
int a,b;
cin>>n>>q;
build(1,1,n-1);
for(int i=0;i<q;i++){
cin>>a>>b;
//交换以下好排序
if(a>b){
int t=a;
a=b;
b=t;
}
ans[i].l=a+1;
ans[i].r=b;//转化成路的编号
}
sort(ans,ans+q);
ll sum=0;
for(int i=0;i<q;i++){
minn = 1e21;
//查询最小值
query(1,ans[i].l,ans[i].r);
sum+=minn;
//更新区间最小值
add(1,ans[i].l,ans[i].r,minn);
}
printf("%lld\n", sum);
}L3-018 森森美图
分数 60
全屏浏览
切换布局
作者 戴龙翱、朱建科
单位 浙江大学
森森最近想让自己的朋友圈熠熠生辉,所以他决定自己写个美化照片的软件,并起名为森森美图。众所周知,在合照中美化自己的面部而不美化合照者的面部是让自己占据朋友圈高点的绝好方法,因此森森美图里当然得有这个功能。 这个功能的第一步是将自己的面部选中。森森首先计算出了一个图像中所有像素点与周围点的相似程度的分数,分数越低表示某个像素点越“像”一个轮廓边缘上的点。 森森认为,任意连续像素点的得分之和越低,表示它们组成的曲线和轮廓边缘的重合程度越高。为了选择出一个完整的面部,森森决定让用户选择面部上的两个像素点A和B,则连接这两个点的直线就将图像分为两部分,然后在这两部分中分别寻找一条从A到B且与轮廓重合程度最高的曲线,就可以拼出用户的面部了。 然而森森计算出来得分矩阵后,突然发现自己不知道怎么找到这两条曲线了,你能帮森森当上朋友圈的小王子吗?
为了解题方便,我们做出以下补充说明:
- 图像的左上角是坐标原点(0,0),我们假设所有像素按矩阵格式排列,其坐标均为非负整数(即横轴向右为正,纵轴向下为正)。
- 忽略正好位于连接A和B的直线(注意不是线段)上的像素点,即不认为这部分像素点在任何一个划分部分上,因此曲线也不能经过这部分像素点。
- 曲线是八连通的(即任一像素点可与其周围的8个像素连通),但为了计算准确,某像素连接对角相邻的斜向像素时,得分额外增加两个像素分数和的2倍减一。例如样例中,经过坐标为(3,1)和(4,2)的两个像素点的曲线,其得分应该是这两个像素点的分数和(2+2),再加上额外的(2+2)乘以(2−1),即约为5.66。
输入格式:
输入在第一行给出两个正整数N和M(5≤N,M≤100),表示像素得分矩阵的行数和列数。
接下来N行,每行M个不大于1000的非负整数,即为像素点的分值。
最后一行给出用户选择的起始和结束像素点的坐标(Xstart,Ystart)和(Xend,Yend)。4个整数用空格分隔。
输出格式:
在一行中输出划分图片后找到的轮廓曲线的得分和,保留小数点后两位。注意起点和终点的得分不要重复计算。
输入样例:
6 6
9 0 1 9 9 9
9 9 1 2 2 9
9 9 2 0 2 9
9 9 1 1 2 9
9 9 3 3 1 1
9 9 9 9 9 9
2 1 5 4
输出样例:
27.04//题目有点长就讲一下人话
//简单来说就是给两个点把矩阵分成两个部分
//然后就是从起点开始到结束点的最短距离啊
//注意一下边界就行了,题目唯一的难点就是边界划分,最短路径的话
//应该迪杰斯特拉和什么bfs都可以的,额这里是密矩阵啊所以没必要邻接表
//我靠炸了半天,发现emplace必须要写构造方法
#include <bits/stdc++.h>
using namespace std;
const double f=sqrt(2)-1;//根号2-1
int score[100][100],pos[100][100];//pos是用来储存每个点和直线位置的关系
bool vis[100][100]; //是否访问
double dis[100][100]; //距离
int dir1[2][4] = {{1, -1, 0, 0}, {0, 0, 1, -1}}; //上下左右方向
int dir2[2][4] = {{1, 1, -1, -1}, {1, -1, 1, -1}}; //斜对角方向
int n,m;
//这里为了统一我们约定结构体里面的xy指的是矩阵的行和列并不是实际的坐标
struct node{
int x,y;
}start,endq;
struct node1{
int x, y;
double dis;
node1(int x,int y,double dis){
this->x=x;
this->y=y;
this->dis=dis;
}
//便于用优先队列优化迪杰斯特拉算法,不会的就手写或者额bfs直接秒
friend bool operator<(node1 a, node1 b) {
return a.dis > b.dis;
}
};
//函数用来返回点和直线的关系,高中知识啊,不会的自己去查(三角形面积向量公式)
int nodejudge(struct node p1,struct node p2,struct node p3){
int r;
r=(p1.x-p3.x)*(p2.y-p3.y)-(p1.y-p3.y)*(p2.x-p3.x);
if(r>0)
return 1; //右侧
else if(r<0)
return 2; //左侧
return 0; //在线上
}
//用来一侧一侧处理
void init(int flag){
memset(vis,0,sizeof(vis));
for(int i=0;i<n;i++){ //为了避免另一侧被访问,我们直接把另一侧变成1
for(int j=0;j<m;j++){
if(pos[i][j]==flag||pos[i][j]==0){
vis[i][j]=1;
}
}
}
vis[start.y][start.x]=0;
vis[endq.y][endq.x]=0; //这两个点可以访问
for(int i=0;i<n;i++){
for(int j=0;j<m;j++){
dis[i][j]=9999999;
}
}
}
void digs(){
dis[start.y][start.x]=0;
priority_queue<node1> q;
q.emplace(start.x,start.y,0);
while(q.size()){
node1 t=q.top();
q.pop();
if(t.y==endq.y&&t.x==endq.x)
return ;//到终点了
if(vis[t.y][t.x])
continue;//如果说已经搞过了就直接跑
vis[t.y][t.x]=1;
for(int i=0;i<4;i++){ //上下左右
int xx=t.x+dir1[0][i];
if(xx<0||xx>=m)
continue;//越界了
int yy=t.y+dir1[1][i];
if(yy<0||yy>=n)
continue;//越界了
if(vis[yy][xx])
continue;
if(t.dis+score[yy][xx]<dis[yy][xx]){
dis[yy][xx]=t.dis+score[yy][xx];
q.emplace(xx,yy,dis[yy][xx]); //其实里面就算有重复的也无所谓,反正vis已经为1了
}
}
for(int i=0;i<4;i++){ //斜对角
int xx=t.x+dir2[0][i];
int yy=t.y+dir2[1][i];
if(xx<0||xx>=m)
continue;
if(yy<0||yy>=n)
continue;
if (t.dis+score[yy][xx]+f*(score[yy][xx]+score[t.y][t.x])<dis[yy][xx]){
dis[yy][xx]=t.dis+score[yy][xx]+f*(score[yy][xx]+score[t.y][t.x]);
q.emplace(xx,yy,dis[yy][xx]);
}
}
}
}
int main(){
cin>>n>>m;
double sum=0;//总长度
for(int i=0;i<n;i++){
for(int j=0;j<m;j++){
cin>>score[i][j];
}
}
cin>>start.x>>start.y>>endq.x>>endq.y;
for(int i=0;i<n;i++){
for(int j=0;j<m;j++){
struct node k;
//这里尤其要注意以下,x坐标在这里是j而不是i
k.x=j;
k.y=i;
pos[i][j]=nodejudge(start,endq,k);
}
}
init(1);//先处理一侧
digs();
sum+=dis[endq.y][endq.x];
init(2);//先处理一侧
digs();
sum+=dis[endq.y][endq.x];
//最后别忘了减去重复计算的终点以及没有进入计算的起点
sum+=score[start.y][start.x];
sum-=score[endq.y][endq.x];
printf("%.2lf",sum);
}
L3-019 代码排版
分数 60
全屏浏览
切换布局
作者 陈越
单位 浙江大学
某编程大赛中设计有一个挑战环节,选手可以查看其他选手的代码,发现错误后,提交一组测试数据将对手挑落马下。为了减小被挑战的几率,有些选手会故意将代码写得很难看懂,比如把所有回车去掉,提交所有内容都在一行的程序,令挑战者望而生畏。
为了对付这种选手,现请你编写一个代码排版程序,将写成一行的程序重新排版。当然要写一个完美的排版程序可太难了,这里只简单地要求处理C语言里的for、while、if-else这三种特殊结构,而将其他所有句子都当成顺序执行的语句处理。输出的要求如下:
- 默认程序起始没有缩进;每一级缩进是 2 个空格;
- 每行开头除了规定的缩进空格外,不输出多余的空格;
- 顺序执行的程序体是以分号“;”结尾的,遇到分号就换行;
- 在一对大括号“{”和“}”中的程序体输出时,两端的大括号单独占一行,内部程序体每行加一级缩进,即:
{
程序体
}
- for的格式为:
for (条件) {
程序体
}
- while的格式为:
while (条件) {
程序体
}
- if-else的格式为:
if (条件) {
程序体
}
else {
程序体
}
输入格式:
输入在一行中给出不超过 331 个字符的非空字符串,以回车结束。题目保证输入的是一个语法正确、可以正常编译运行的 main 函数模块。
输出格式:
按题面要求的格式,输出排版后的程序。
输入样例:
int main() {int n, i; scanf("%d", &n);if( n>0)n++;else if (n<0) n--; else while(n<10)n++; for(i=0; i<n; i++ ){ printf("n=%d\n", n);}return 0; }
输出样例:
int main()
{
int n, i;
scanf("%d", &n);
if ( n>0) {
n++;
}
else {
if (n<0) {
n--;
}
else {
while (n<10) {
n++;
}
}
}
for (i=0; i<n; i++ ) {
printf("n=%d\n", n);
}
return 0;
}#include <cstring>
#include <string>
#include <algorithm>
#include <cstdio>
#include <iostream>
using namespace std;
//判断语句类型
int judge(string dat, int i){
int is;
if(dat.find("if", i) == i && (dat[i+2]==' ' || dat[i+2]=='('))
is = 2;
else if(dat.find("while", i) == i && (dat[i+5]==' ' || dat[i+5]=='('))
is = 5;
else if(dat.find("for", i) == i && (dat[i+3]==' ' || dat[i+3]=='('))
is = 3;
else if(dat.find("else", i) == i && dat[i+4]==' ')
is = 4;
else if(dat.find("{", i) == i)
is = 1;
else
is = 0; //普通语句
return is;
}
//打印空格
void printspace(int space){
for(int z=0; z<space; z++)
cout<<" ";
}
//跳过多余空格
void tiao(string dat, int &i){
while(dat[i]==' ')
i++;
}
int main(){
string dat;
bool flag;
getline(cin, dat);
int i=0,j=0;
int m;
int idx;
int k;
int tmp;
int space=0;
int debt=0;
//处理main函数 开端部分
tiao(dat,i);
//从初始字符打印至)
idx = dat.find(')', 0);//从下标0开始找
for(j=i; j<=idx; j++)
cout<<dat[j];
cout<<endl;
cout<<"{"<<endl;
//跳过字符串中的{, 因为上边已经直接打印
space += 2;
i=dat.find('{',0);
i++;
while(i < dat.length()){
tiao(dat, i);
if((tmp = judge(dat, i))){
printspace(space);
if(tmp == 1){
cout<<"{"<<endl;
i++;
space += 2;
continue;
}
//else特殊处理,其他的for、while、if可归为一种 均是for/while/if + () + { }
if(tmp == 4){
for(j=0; j<4; j++)
cout<<dat[i+j];
k = i+3;
}
else{
for(j=0; j<tmp; j++)
cout<<dat[i+j];
cout<<" ";
i += tmp;
tiao(dat, i);
k = i;
int t=0;
while(true){
if(dat[k] == '('){
t++;
}
else if(dat[k] == ')'){
t--;
if(!t) break;
}
k++;
}
for(j=i; j<=k; j++)
cout<<dat[j];
}
m = k+1;
tiao(dat, m);
if(dat[m] != '{'){
cout<<" {"<<endl;
flag = false;
debt++;
i = m;
}else{
cout<<" {"<<endl;
flag = true;
i = m+1;
}
space += 2;
}
else if(dat[i] == '}'){
space -= 2;
printspace(space);
cout<<"}"<<endl;
if(space == 0)
break;//字符串最后可能由空格
i++;
tiao(dat, i);
while(debt && judge(dat, i)!=4){
space -= 2;
printspace(space);
cout<<"}"<<endl;
debt--;
}
}
else{
//普通语句
idx = dat.find(';', i);
printspace(space);
for(j=i; j<=idx; j++)
cout<<dat[j];
cout<<endl;
i = idx+1;
if(debt && !flag){
space -= 2;
printspace(space);
cout<<"}"<<endl;
debt--;
//下边几行代码同为判断上述情况一,是否应该输出 }
tiao(dat, i);
while(debt && judge(dat, i)!=4){
space -= 2;
debt--;
printspace(space);
cout<<"}"<<endl;
}
}
}
}
return 0;
}
L3-020 至多删三个字符
分数 80
全屏浏览
切换布局
作者 曹鹏
单位 Google
给定一个全部由小写英文字母组成的字符串,允许你至多删掉其中 3 个字符,结果可能有多少种不同的字符串?
输入格式:
输入在一行中给出全部由小写英文字母组成的、长度在区间 [4, 106] 内的字符串。
输出格式:
在一行中输出至多删掉其中 3 个字符后不同字符串的个数。
输入样例:
ababcc
输出样例:
25
提示:
删掉 0 个字符得到 "ababcc"。
删掉 1 个字符得到 "babcc", "aabcc", "abbcc", "abacc" 和 "ababc"。
删掉 2 个字符得到 "abcc", "bbcc", "bacc", "babc", "aacc", "aabc", "abbc", "abac" 和 "abab"。
删掉 3 个字符得到 "abc", "bcc", "acc", "bbc", "bac", "bab", "aac", "aab", "abb" 和 "aba"。
//第一眼我觉得暴力应该不行。这道题应该跟二进制有点关系
//后来想想也不对,二进制表示不了
//这道题涉及到了去重,动归也太操蛋了
//动态规划比较好算方案数但是不好去重就挺难受的
#include<iostream>
//这里注意,大空间分配要在全局变量
const int N=1e6+10;
long f[N][4];//用来dp,表示第i个字符串删除字符串的方案数
using namespace std;
int main(){
int n;
string s;
cin>>s;
s=" "+s;
n=s.size()-1;
f[0][0]=1;
for(int i=1;i<=n;i++){
for(int j=0;j<=3;j++){//这边一定是从小往大的删,不知道的额嘿嘿
if(i<j)
break;
f[i][j]=f[i-1][j];
if(j!=0)
f[i][j]+=f[i-1][j-1];//这里就是不删和删的方案加一起
//去重
for(int x=i-1;x>=1&&j-(i-x)>=0;x--){
if(s[x]==s[i]){//意思就是说如果发现了一样的,x与i,x+1与i+1的情况是一样的要减掉
f[i][j]-=f[x-1][j-(i-x)];
break;
}
}
}
}
long sum=0;
for(int i=0;i<=3;i++)
sum+=f[n][i];
cout<<sum;
}
L3-021 神坛
分数 80
全屏浏览
切换布局
作者 邓俊辉
单位 清华大学
在古老的迈瑞城,巍然屹立着 n 块神石。长老们商议,选取 3 块神石围成一个神坛。因为神坛的能量强度与它的面积成反比,因此神坛的面积越小越好。特殊地,如果有两块神石坐标相同,或者三块神石共线,神坛的面积为 0.000。
长老们发现这个问题没有那么简单,于是委托你编程解决这个难题。
输入格式:
输入在第一行给出一个正整数 n(3 ≤ n ≤ 5000)。随后 n 行,每行有两个整数,分别表示神石的横坐标、纵坐标(−109≤ 横坐标、纵坐标 <109)。
输出格式:
在一行中输出神坛的最小面积,四舍五入保留 3 位小数。
输入样例:
8
3 4
2 4
1 1
4 1
0 3
3 0
1 3
4 2
输出样例:
0.500
样例解释
输出的数值等于图中红色或紫色框线的三角形的面积。
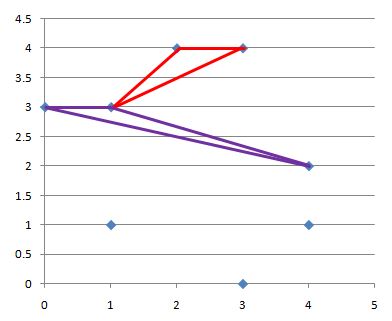
//题目不算很难,主要的是怎么比较三角形的面积
//额如果暴力就是n^3次复杂度了,肯定过不了
//采用的方法是极角排序,但讲真的极角排序并不是一个最好的方法
//并不是很合理,先码一下
#include<iostream>
#include<cmath>
#include<algorithm>
using namespace std;
struct xiangl{
long long x;
long long y;
};
bool cmp(struct xiangl a,struct xiangl b){
if(a.x*b.y==b.x*a.y)
return a.x<b.y;
return a.x*b.y>b.x*a.y;//这里不是ab相比较,看的是叉乘大于0,就是选较小的那个角
}
int main(){
int n;
double ans=1e9;
cin>>n;
struct xiangl point[5000];
struct xiangl line[5000];
for(int i=0;i<n;i++){
cin>>point[i].x>>point[i].y;
}
for(int i=0;i<n;i++){
int t=0;
for(int j=0;j<n;j++){
if(i==j)
continue;
line[t].x=point[i].x-point[j].x;
line[t].y=point[i].y-point[j].y;
t++;//计算向量
}
sort(line,line+t,cmp);
for(int j=1;j<t;j++) {
//这边注意一下三角型的面积公式=1/2absint
ans=min(ans,0.5*abs(line[j-1].x*line[j].y-line[j-1].y*line[j].x));
}
}
printf("%.3f",ans);
}
L3-022 地铁一日游
分数 80
全屏浏览
切换布局
作者 戴龙翱
单位 杭州百腾教育科技有限公司
森森喜欢坐地铁。这个假期,他终于来到了传说中的地铁之城——魔都,打算好好过一把坐地铁的瘾!
魔都地铁的计价规则是:起步价 2 元,出发站与到达站的最短距离(即计费距离)每 K 公里增加 1 元车费。
例如取 K = 10,动安寺站离魔都绿桥站为 40 公里,则车费为 2 + 4 = 6 元。
为了获得最大的满足感,森森决定用以下的方式坐地铁:在某一站上车(不妨设为地铁站 A),则对于所有车费相同的到达站,森森只会在计费距离最远的站或线路末端站点出站,然后用森森美图 App 在站点外拍一张认证照,再按同样的方式前往下一个站点。
坐着坐着,森森突然好奇起来:在给定出发站的情况下(在出发时森森也会拍一张照),他的整个旅程中能够留下哪些站点的认证照?
地铁是铁路运输的一种形式,指在地下运行为主的城市轨道交通系统。一般来说,地铁由若干个站点组成,并有多条不同的线路双向行驶,可类比公交车,当两条或更多条线路经过同一个站点时,可进行换乘,更换自己所乘坐的线路。举例来说,魔都 1 号线和 2 号线都经过人民广场站,则乘坐 1 号线到达人民广场时就可以换乘到 2 号线前往 2 号线的各个站点。换乘不需出站(也拍不到认证照),因此森森乘坐地铁时换乘不受限制。
输入格式:
输入第一行是三个正整数 N、M 和 K,表示魔都地铁有 N 个车站 (1 ≤ N ≤ 200),M 条线路 (1 ≤ M ≤ 1500),最短距离每超过 K 公里 (1 ≤ K ≤ 106),加 1 元车费。
接下来 M 行,每行由以下格式组成:
<站点1><空格><距离><空格><站点2><空格><距离><空格><站点3> ... <站点X-1><空格><距离><空格><站点X>
其中站点是一个 1 到 N 的编号;两个站点编号之间的距离指两个站在该线路上的距离。两站之间距离是一个不大于 106 的正整数。一条线路上的站点互不相同。
注意:两个站之间可能有多条直接连接的线路,且距离不一定相等。
再接下来有一个正整数 Q (1 ≤ Q ≤ 200),表示森森尝试从 Q 个站点出发。
最后有 Q 行,每行一个正整数 **Xi**,表示森森尝试从编号为 Xi 的站点出发。
输出格式:
对于森森每个尝试的站点,输出一行若干个整数,表示能够到达的站点编号。站点编号从小到大排序。
输入样例:
6 2 6
1 6 2 4 3 1 4
5 6 2 6 6
4
2
3
4
5
输出样例:
1 2 4 5 6
1 2 3 4 5 6
1 2 4 5 6
1 2 4 5 6//又是一道很长的题目,简单点来说就是给一张图,然后就是找车费相同但是能到达的最长距离
//点的计算只计算线路的端点,站点是200个,且不是稀疏矩阵可以考虑邻接矩阵
#include<iostream>
#include<map>
#include<vector>
using namespace std;
//路线结构体
struct Line{
vector<int> road;//具体路线
int visit=0; //标记这个点是不是被访问过
int end=0; //标记这个点是不是端点
}line[201];//这个实际上就是一个邻接表,下标是开始端点
void search(int i,int vis){
for(int it : line[i].road){
if(line[it].visit != vis){
line[it].visit = vis;
search(it, vis);
}
}
}
const long long Max=1e9+1;
int g[201][201];
int main(){
int n,m,k;
cin>>n>>m>>k;
for(int i=1;i<=n;i++){
for(int j=1;j<=n;j++){
g[i][j]=Max;
}
}
for(int i=0;i<m;i++){
int a;
cin>>a;
line[a].end=1;
int dis,b;//分别读取路径长和端点
while(getchar()!='\n'){
cin>>dis>>b;
//这里是因为我们的图里面只选取最短的路径
if(g[a][b]>dis){
g[a][b]=dis;
g[b][a]=dis;
}
a=b;
}
line[a].end=1;
}
//接下来我们直接弗洛伊德算法
for(int k=1;k<=n;k++){
for(int i=1;i<=n;i++){
for(int j=1;j<=n;j++){
if(i!=j&&g[i][j]>g[i][k]+g[k][j])
g[i][j]=g[i][k]+g[k][j];
}
}
}
for(int i=1;i<=n;i++){
map<int,int> m;
//寻找每个费用的最长距离
for(int j=1;j<=n;j++){
if(g[i][j]!=Max&&g[i][j]>m[2+g[i][j]/k])
m[2+g[i][j]/k]=g[i][j];
}
for(int j=1;j<=n;j++){
if (g[i][j] == m[2+g[i][j]/k]||(i!=j&&line[j].end &&g[i][j]!=Max))
line[i].road.push_back(j);
}
}
int q;
cin>>q;
int flag;
int start;
for(int i=1;i<=q;i++){
cin>>start;
line[start].visit=i;
flag=0;
search(start, i); //搜索
for(int j=1;j<=n;j++)
if(line[j].visit==i){
printf("%s%d", flag?" ": "",j);
flag = 1;
}
cout<<endl;
}
}
L3-023 计算图
分数 80
全屏浏览
切换布局
作者 陈翔
单位 浙江大学
“计算图”(computational graph)是现代深度学习系统的基础执行引擎,提供了一种表示任意数学表达式的方法,例如用有向无环图表示的神经网络。 图中的节点表示基本操作或输入变量,边表示节点之间的中间值的依赖性。 例如,下图就是一个函数
f(x1,x2)=lnx1+x1x2−sinx2
的计算图。
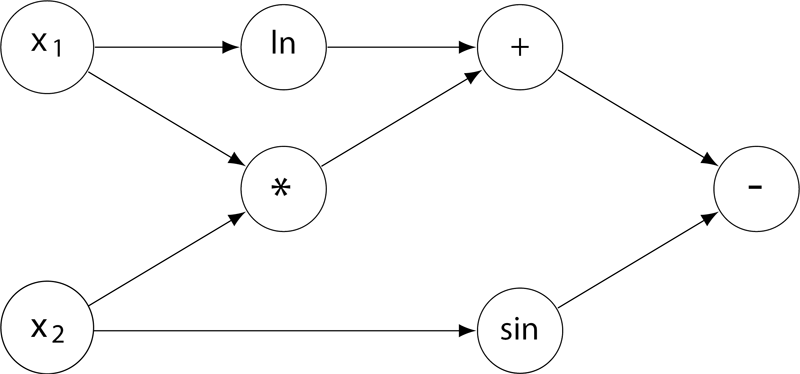
现在给定一个计算图,请你根据所有输入变量计算函数值及其偏导数(即梯度)。 例如,给定输入x1=2,x2=5,上述计算图获得函数值 f(2,5)=ln(2)+2×5−sin(5)=11.652;并且根据微分链式法则,上图得到的梯度 ∇f=[∂f/∂x1,∂f/∂x2]=[1/x1+x2,x1−cosx2]=[5.500,1.716]。
知道你已经把微积分忘了,所以这里只要求你处理几个简单的算子:加法、减法、乘法、指数(ex,即编程语言中的 exp(x) 函数)、对数(lnx,即编程语言中的 log(x) 函数)和正弦函数(sinx,即编程语言中的 sin(x) 函数)。
友情提醒:
- 常数的导数是 0;x 的导数是 1;ex 的导数还是 ex;lnx 的导数是 1/x;sinx 的导数是 cosx。
- 回顾一下什么是偏导数:在数学中,一个多变量的函数的偏导数,就是它关于其中一个变量的导数而保持其他变量恒定。在上面的例子中,当我们对 x1 求偏导数 ∂f/∂x1 时,就将 x2 当成常数,所以得到 lnx1 的导数是 1/x1,x1x2 的导数是 x2,sinx2 的导数是 0。
- 回顾一下链式法则:复合函数的导数是构成复合这有限个函数在相应点的导数的乘积,即若有 u=f(y),y=g(x),则 du/dx=du/dy⋅dy/dx。例如对 sin(lnx) 求导,就得到 cos(lnx)⋅(1/x)。
如果你注意观察,可以发现在计算图中,计算函数值是一个从左向右进行的计算,而计算偏导数则正好相反。
输入格式:
输入在第一行给出正整数 N(≤5×104),为计算图中的顶点数。
以下 N 行,第 i 行给出第 i 个顶点的信息,其中 i=0,1,⋯,N−1。第一个值是顶点的类型编号,分别为:
- 0 代表输入变量
- 1 代表加法,对应 x1+x2
- 2 代表减法,对应 x1−x2
- 3 代表乘法,对应 x1×x2
- 4 代表指数,对应 ex
- 5 代表对数,对应 lnx
- 6 代表正弦函数,对应 sinx
对于输入变量,后面会跟它的双精度浮点数值;对于单目算子,后面会跟它对应的单个变量的顶点编号(编号从 0 开始);对于双目算子,后面会跟它对应两个变量的顶点编号。
题目保证只有一个输出顶点(即没有出边的顶点,例如上图最右边的 -),且计算过程不会超过双精度浮点数的计算精度范围。
输出格式:
首先在第一行输出给定计算图的函数值。在第二行顺序输出函数对于每个变量的偏导数的值,其间以一个空格分隔,行首尾不得有多余空格。偏导数的输出顺序与输入变量的出现顺序相同。输出小数点后 3 位。
输入样例:
7
0 2.0
0 5.0
5 0
3 0 1
6 1
1 2 3
2 5 4
输出样例:
11.652
5.500 1.716//网上都是什么dfs深搜???看不了一点直接拓步排序秒啦
//就是有点绕,每个点都要四个数组,入度,节点中的值每次计算都要更新,两个操作数
#include <iostream>
#include <algorithm>
#include <cmath>
#include <vector>
#include <queue>
using namespace std;
int op[50000];//操作符
int a[50000], b[50000];//操作数
int in[50000];//入度
double num[50000];//结点上的值
vector<double> p[50000];//用来记录偏导数动态规划思想
vector<int> g[50000];//邻接表
vector<int> x;//保存输入变量,准确来说是下标
int main(){
int n;
cin >> n;
for(int i = 0; i < n; i++){
cin>>op[i];
if(op[i] == 0){
cin>>num[i];
x.push_back(i);
}
if(op[i]==1||op[i]==2||op[i]==3){
cin>>a[i]>>b[i];
g[a[i]].push_back(i);
g[b[i]].push_back(i);
in[i] += 2;
}
if(op[i]==4||op[i]==5||op[i]==6){
cin>>a[i];
g[a[i]].push_back(i);
in[i]++;
}
}
for(int i = 0; i < n; i++)
for(int j = 0; j < x.size(); j++)
p[i].push_back(0);
queue<int> q;
for(int i = 0; i < n; i++)
if(in[i] == 0)
q.push(i);
for(int i = 0; i < x.size(); i++)
p[x[i]][i] = 1;
int final;//记录终点
while(q.size()!=0){
int now = q.front();
q.pop();
if(op[now] == 1){
num[now] = num[a[now]]+num[b[now]];
for(int i = 0; i < x.size(); i++)
p[now][i] = p[a[now]][i]+p[b[now]][i];
}
if(op[now] == 2){
num[now] = num[a[now]]-num[b[now]];
for(int i = 0; i < x.size(); i++)
p[now][i] = p[a[now]][i]-p[b[now]][i];
}
if(op[now] == 3){
num[now] = num[a[now]]*num[b[now]];
for(int i = 0; i < x.size(); i++)
p[now][i] = p[a[now]][i]*num[b[now]]+p[b[now]][i]*num[a[now]];
}
if(op[now] == 4){
num[now] = exp(num[a[now]]);
for(int i = 0; i < x.size(); i++)
p[now][i] = num[now]*p[a[now]][i];
}
if(op[now] == 5){
num[now] = log(num[a[now]]);
for(int i = 0; i < x.size(); i++)
p[now][i] = 1/num[a[now]]*p[a[now]][i];
}
if(op[now] == 6){
num[now] = sin(num[a[now]]);
for(int i = 0; i < x.size(); i++)
p[now][i] = cos(num[a[now]])*p[a[now]][i];
}
for(int i = 0; i < g[now].size(); i++){
int v = g[now][i];
in[v]--;
if(in[v] == 0)
q.push(v);
}
final = now;
}
printf("%.3f\n", num[final]);
printf("%.3f", p[final][0]);
for(int i = 1; i < x.size(); i++)
printf(" %.3f", p[final][i]);
}
L3-024 Oriol和David
分数 85
全屏浏览
切换布局
作者 李文新
单位 北京大学
Oriol 和 David 在一个边长为 16 单位长度的正方形区域内,初始位置分别为(7, 7)和(8, 8)。现在有 20 组、每组包含 20 个位置需要他们访问,位置以坐标(x, y)的形式给出,要求在时间 120 秒内访问尽可能多的点。(x和y均为正整数,且0 ≤ x < 16,0 ≤ y < 16)
注意事项:
- 针对任意一个位置,Oriol或David中的一人到达即视为访问成功;
- Oriol和David必须从第 1 组位置开始访问,且必须访问完第 i 组全部20个位置之后,才可以开始第 i + 1 组 20 个位置的访问。同组间各位置的访问顺序可自由决定;
- Oriol和David在完成当前组位置的访问后,无需返回开始位置、可以立即开始下一组位置的访问;
- Oriol和David可以向任意方向移动,移动时速率为 2 单位长度/秒;移动过程中,无任何障碍物阻拦。
输入格式:
输入第一行是一个正整数 T (T ≤ 10),表示数据组数。接下来给出 T 组数据。
对于每组数据,输入包含 20 组,每组 1 行,每行由 20 个坐标组成,每个坐标由 2 个整数 x 和 y 组成,代表 Oriol 和 David 要访问的 20 组 20 个位置的坐标;0 ≤ x < 16,0 ≤ y < 16,均用一个空格隔开。
输出格式:
每组数据输出的第一行是一个整数N,代表分配方案访问过的位置组数;
接下来的N组每组的第一行包含两个整数 Ba 和 Bb,分别代表每组分配方案中 Oriol 和 David 负责访问的位置数,第二行和第三行分别包含 Ba 和 Bb 个整数 i,分别代表 Oriol 和 David 负责访问的位置在组内的序号(从0开始计数)。
0 ≤ N ≤ 20,0 ≤ Ba ≤ 20,0 ≤ Bb ≤ 20,0 ≤ i ≤ 19。
输入样例:
1
5 5 3 13 8 7 13 6 6 11 2 0 1 14 9 15 8 9 3 12 4 6 2 10 2 5 4 9 4 1 15 0 11 4 10 0 15 5 10 14
1 0 14 8 0 7 6 8 4 12 12 8 9 8 10 14 9 4 13 4 9 1 2 1 0 2 11 10 7 15 9 6 13 11 3 5 4 5 10 7
7 3 8 13 15 0 5 4 2 8 7 14 4 13 11 1 8 15 4 5 4 7 7 10 6 7 13 4 6 2 9 13 1 12 10 7 10 5 5 11
5 8 12 12 11 5 12 9 2 2 11 15 5 14 0 0 14 0 2 5 7 3 10 1 2 8 4 2 4 8 9 14 1 11 1 9 15 7 3 3
1 9 10 14 7 3 15 5 5 15 3 2 12 11 8 10 3 3 11 5 7 4 6 11 6 1 4 10 11 13 12 4 3 4 1 3 7 5 13 11
3 11 9 8 12 9 14 10 11 13 5 5 4 11 1 12 13 2 10 14 5 15 10 15 11 0 3 6 7 11 4 9 15 0 12 14 10 10 13 11
10 4 9 12 0 13 6 6 7 10 11 15 6 14 1 2 4 9 8 5 4 0 13 11 5 3 13 3 9 8 2 4 13 14 12 12 14 2 8 15
2 8 4 9 13 10 8 5 2 13 12 6 4 4 10 6 14 13 11 5 12 1 6 0 11 2 8 15 12 4 13 8 8 2 9 7 7 13 0 9
0 0 4 0 2 3 10 2 7 3 9 4 2 13 11 11 1 8 11 15 11 2 8 11 10 15 7 9 13 15 15 10 1 2 11 9 14 6 5 5
2 13 6 8 7 14 8 5 15 14 5 6 4 10 14 12 3 14 0 5 4 1 0 14 13 14 12 5 5 9 1 2 2 12 4 8 1 15 7 11
10 5 15 7 6 8 11 10 7 13 14 0 12 2 9 12 4 5 3 8 8 13 7 12 15 15 12 9 15 6 14 3 9 6 15 12 7 9 4 15
0 10 6 2 3 2 6 3 14 6 10 13 3 10 15 9 10 0 7 0 14 15 1 2 13 9 11 11 10 3 6 13 0 14 11 2 9 8 15 5
3 9 13 11 1 1 0 9 5 4 4 9 4 13 10 1 12 11 4 2 0 4 1 7 4 10 4 0 2 1 2 0 13 2 11 10 0 5 15 3
15 11 8 1 12 5 8 5 7 5 7 7 2 4 0 4 7 3 12 6 9 15 5 12 14 11 15 10 8 11 4 10 4 14 13 10 4 4 2 12
9 12 15 13 0 12 0 14 3 1 10 15 15 11 1 12 3 0 5 2 15 10 8 4 9 1 8 0 1 13 2 7 12 13 14 10 6 0 13 15
13 7 14 15 9 4 8 2 7 3 7 11 2 13 5 0 13 5 4 0 12 2 3 2 11 15 9 2 9 7 3 7 4 5 14 5 14 12 9 13
12 11 2 14 2 6 6 12 5 15 13 11 2 0 9 13 7 1 7 11 4 4 2 10 0 8 5 3 6 13 2 7 2 15 6 8 3 5 8 11
12 5 9 9 4 14 3 2 14 2 2 1 9 11 8 10 2 14 12 15 0 13 4 7 0 0 0 6 0 1 4 13 4 3 3 10 15 2 10 10
11 15 8 5 6 15 9 8 2 7 15 14 1 10 14 6 13 6 0 15 4 1 3 12 7 8 12 4 0 10 7 10 0 14 13 5 11 1 15 6
1 12 13 14 6 12 9 0 6 8 3 15 5 4 4 2 15 10 3 6 13 12 8 4 15 3 1 5 7 1 6 14 8 6 2 6 11 3 4 4
输出样例:
2
10 10
1 2 3 4 5 6 7 8 9 0
11 12 13 14 15 16 17 18 19 10
1 19
1
0 2 3 4 5 6 7 8 9 11 12 13 14 15 16 17 18 19 10
注意:样例只代表格式,不具有特别含义。
评分方式:
本题按照你给出的方案的优良程度评定分数。
具体评分规则如下:
- 本题所有数据点输入均为一样的数据;
- 评分时,假定输入有 X 组数据,则你的评分答案为你的程序在所有 X 组数据中答案的平均值;
- 例如,你对 3 组数据,分别访问了 3 个、5 个、8 个点,则你的评分答案为 5.33333...
- 特别的,如果你输出的答案中有任意一组不合法,则你的评分答案恒定为 0;
- 输出方案行走超过 120 秒仍然合法,答案计算时只计算 120 秒内的部分;
- 评测时,从 0 开始的测试点的标准答案依次增大,只有评分答案超过标准答案时,你才可以得到对应测试点的分数。
不合法的情况如下:
- 输出格式不正确;
- 重复访问自己已访问的点;(但可以经过)
- 访问不存在的点。
部分评分标准答案如下:
- 第 0 号点:20;(即需要访问平均 20 个点才可以获得该点分数)
- 第 1 号点:70;(同上)
- 第 2 号点:90;
- 第 7 号点:150。
//这个题目就暴力一点吧,具体思路就是我们直接读取20个点,然后直接两个点开始出发
//分别找距离他们各自最短的点,如果说他们两个找了一个相同的点,那么选距离短的
//最后要分别记录他们的路径,遍历20个点结束后选取时间长的那一条路线
//为了方便计算,我们只在一个方案结束后计算时间
//注意中间不要重复调用函数,不然会有bug
//好的我靠能过120点为什么就对了第一个
//我靠不想想了,结束,题目表达都不是很明确,骗点分算了
#include<iostream>
#include<vector>
#include<cmath>
using namespace std;
struct point{
double x,y;
void set(double _x,double _y){
x=_x;
y=_y;
}
};
//他两当前分别所在的点
struct point Oriol;
struct point David;
//记录他俩的路线,每组数据记得清除
vector<int> ori;
vector<int> da;
vector<vector<int>> zong1;//由于最后不能一组一组输出,所以我们要把路线储存
vector<vector<int>> zong2;
struct point G[20];
int visit[20];//判断该点是否被访问过
//计算两点之间的距离
double dis(struct point a,struct point b){
return sqrt(pow((a.x-b.x),2)+pow((a.y-b.y),2));
}
//查找距离该点最短的点
int getclose(struct point a){
int index=-1;
double mindis=999999;
//这里实际上还能优化,假如两个点距离都相同,那么可能还要回溯一下找最优解
for(int i=0;i<20;i++){
if(mindis>dis(a,G[i])&&visit[i]==0){
mindis=dis(a,G[i]);
index=i;
}
}
return index;
}
int main(){
int T;
cin>>T;
while(T--){
//每一组的开始
double totaltime=120;
Oriol.set(7,7);
David.set(8,8);
zong1.clear();
zong2.clear();
for(int i=0;i<20;i++){
ori.clear();
da.clear();
double time1=0;//用来记录时间
double time2=0;
for(int j=0;j<20;j++){
visit[j]=0;//全部点标记为0
}
for(int j=0;j<20;j++){
double x,y;
cin>>x>>y;
G[j].set(x,y);
}
//这边随便找个点就行了,只是判断是不是找完了
while(getclose(Oriol)!=-1){
int index1=getclose(Oriol);
int index2=getclose(David);
if(index1==index2){
double a=dis(G[index1],Oriol);
double b=dis(G[index2],David);
if(a>b){
da.push_back(index2);
visit[index2]=1;
David.set(G[index2].x,G[index2].y);
time2=time2+b/2.0;
index1=getclose(Oriol);
ori.push_back(index1);
visit[index1]=1;
Oriol.set(G[index1].x,G[index1].y);
a=dis(G[index1],Oriol);
time1=time1+a/2.0;
}
else{
ori.push_back(index1);
visit[index1]=1;
Oriol.set(G[index1].x,G[index1].y);
time1=time1+a/2.0;
//cout<<dis(G[index1],Oriol)<<endl;
index2=getclose(David);
da.push_back(index2);
visit[index2]=1;
David.set(G[index2].x,G[index2].y);
b=dis(G[index1],David);
time2=time2+b/2.0;
}
}
else{
double a=dis(G[index1],Oriol);
double b=dis(G[index2],David);
ori.push_back(index1);
da.push_back(index2);
visit[index1]=1;
visit[index2]=1;
Oriol.set(G[index1].x,G[index1].y);
David.set(G[index2].x,G[index2].y);
time1=time1+a/2.0;
time2=time2+b/2.0;
//cout<<dis(G[index2],David)<<endl;
}
}
//查找完毕之后我们需要判断两个人的路径长度并计算时间
zong1.push_back(ori);
zong2.push_back(da);
if(time1>time2){
totaltime-=time1;
}
else{
totaltime-=time2;
}
if(totaltime<=0){
//说明时间已经到了,我们直接输出
cout<<i+1<<endl;
//由于zong里面个数一样我们随便找一个
for(int j=0;j<zong1.size();j++){
cout<<zong1[j].size()<<" "<<zong2[j].size()<<endl;
for(int k=0;k<zong1[j].size();k++){
if(k==0)
cout<<zong1[j][k];
else
cout<<" "<<zong1[j][k];
}
cout<<endl;
for(int k=0;k<zong2[j].size();k++){
if(k==0)
cout<<zong2[j][k];
else
cout<<" "<<zong2[j][k];
}
cout<<endl;
}
break;
}
}
}
}注意:这道题只能过第一个点,不想思考啦,算是骗骗分吧,如果有人有思路了踢我一下
L3-025 那就别担心了
分数 60
全屏浏览
切换布局
作者 陈越
单位 浙江大学
下图转自“英式没品笑话百科”的新浪微博 —— 所以无论有没有遇到难题,其实都不用担心。
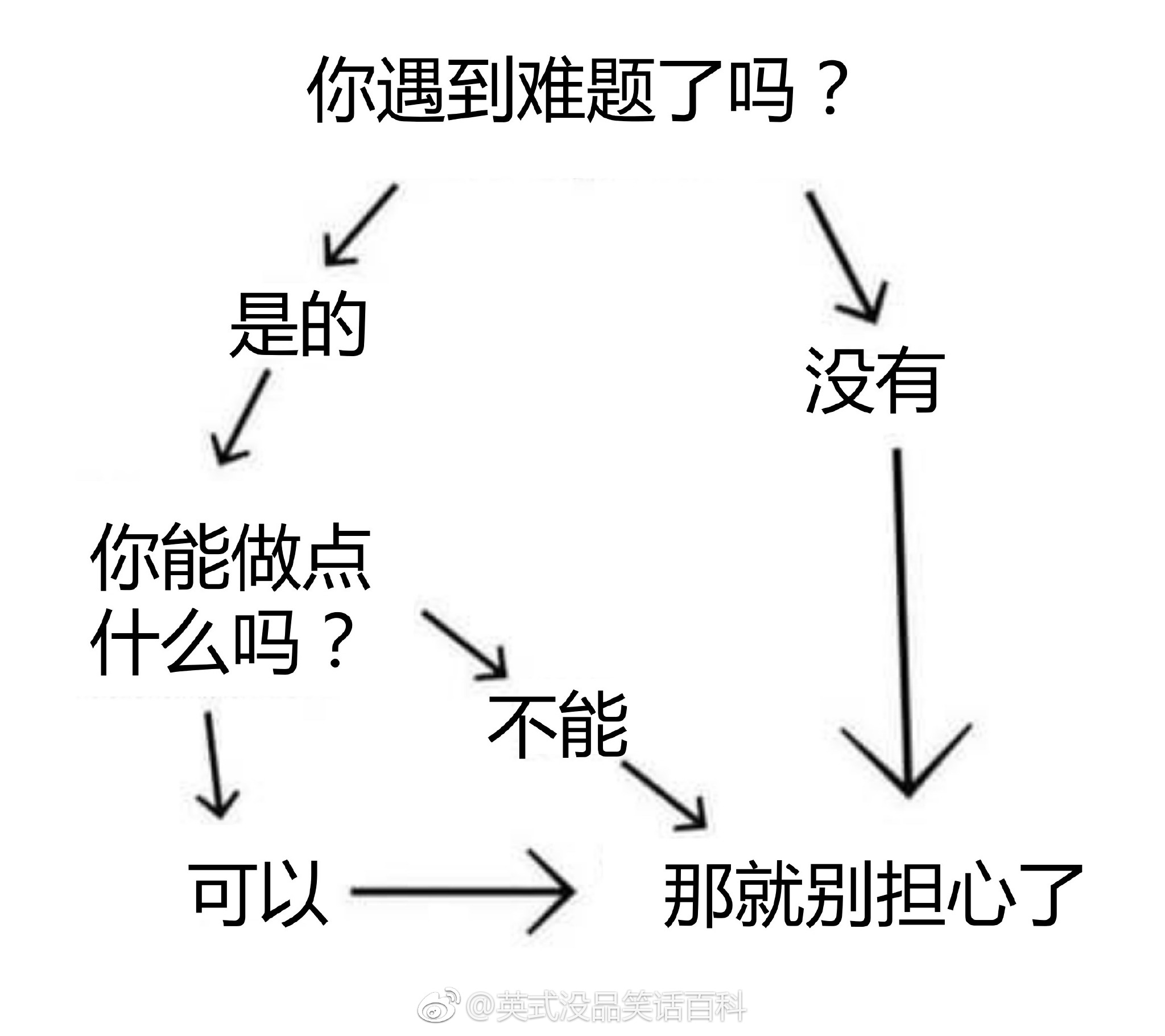
博主将这种逻辑推演称为“逻辑自洽”,即从某个命题出发的所有推理路径都会将结论引导到同一个最终命题(开玩笑的,千万别以为这是真正的逻辑自洽的定义……)。现给定一个更为复杂的逻辑推理图,本题就请你检查从一个给定命题到另一个命题的推理是否是“逻辑自洽”的,以及存在多少种不同的推理路径。例如上图,从“你遇到难题了吗?”到“那就别担心了”就是一种“逻辑自洽”的推理,一共有 3 条不同的推理路径。
输入格式:
输入首先在一行中给出两个正整数 N(1<N≤500)和 M,分别为命题个数和推理个数。这里我们假设命题从 1 到 N 编号。
接下来 M 行,每行给出一对命题之间的推理关系,即两个命题的编号 S1 S2,表示可以从 S1 推出 S2。题目保证任意两命题之间只存在最多一种推理关系,且任一命题不能循环自证(即从该命题出发推出该命题自己)。
最后一行给出待检验的两个命题的编号 A B。
输出格式:
在一行中首先输出从 A 到 B 有多少种不同的推理路径,然后输出 Yes 如果推理是“逻辑自洽”的,或 No 如果不是。
题目保证输出数据不超过 109。
输入样例 1:
7 8
7 6
7 4
6 5
4 1
5 2
5 3
2 1
3 1
7 1
输出样例 1:
3 Yes
输入样例 2:
7 8
7 6
7 4
6 5
4 1
5 2
5 3
6 1
3 1
7 1
输出样例 2:
3 No#include <iostream>
#include <vector>
using namespace std;
const int maxn = 501;
int Road[maxn];
vector<vector<int>> v(maxn);
bool ok = true;
int DFS(int start, int enl) {
if (start == enl) return 1;
if (Road[start] != 0) return Road[start];
for (int i : v[start]) {
if (v[i].empty() && i != enl) {
ok = false;
}
Road[start] += DFS(i, enl);
}
return Road[start];
}
int main() {
ios::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
int N, M, K, D;
cin >> N >> M; // N个命题M个推理
for (int i = 0; i <= N; i++) {
v[i].clear();
}
for (int i = 0; i < M; i++) {
int A, B;
cin >> A >> B;
v[A].push_back(B);
}
cin >> K >> D;
DFS(K, D);
if (Road[K] == 0) ok = false;
cout << Road[K] << (ok ? " Yes" : " No");
return 0;
}
L3-026 传送门
分数 80
全屏浏览
切换布局
作者 WENG, Caizhi
单位 浙江大学
平面上有 2n 个点,它们的坐标分别是 (1,0),(2,0),⋯(n,0) 和 (1,109),(2,109),⋯,(n,109)。我们称这些点中所有 y 坐标为 0 的点为“起点”,所有 y 坐标为 109 的点为终点。一个机器人将从坐标为 (x,0) 的起点出发向 y 轴正方向移动。显然,该机器人最后会到达某个终点,我们设该终点的 x 坐标为 f(x)。
在上述条件下,显然有 f(x)=x。不过这样的数学模型就太无趣了,因此我们对上述数学模型做一些小小的改变。我们将会对模型进行 q 次修改,每一次修改都是以下两种操作之一:
- + x′ x′′ y: 在 (x′,y) 与 (x′′,y) 处增加一对传送门。当机器人碰到其中一个传送门时,它会立刻被传送到另一个传送门处。数据保证进行该操作时,(x′,y) 与 (x′′,y) 处当前不存在传送门。
- - x′ x′′ y: 移除 (x′,y) 与 (x′′,y) 处的一对传送门。数据保证这对传送门存在。
求每次修改后 x=1∑nxf(x) 的值。
输入格式:
第一行输入两个整数 n 与 q (2≤n≤105, 1≤q≤105),代表起点和终点的数量以及修改的次数。
接下来 q 行中,第 i 行输入一个字符 opi 以及三个整数 xi′, xi′′ and yi (opi∈{‘+’ (ascii: 43),‘-’ (ascii: 45)}, 1≤xi′<xi′′≤n, 1≤yi<109),代表第 i 次修改的内容。修改顺序与输入顺序相同。
输出格式:
输出 q 行,其中第 i 行包含一个整数代表第 i 次修改后的答案。
输入样例:
5 4
+ 1 3 1
+ 1 4 3
+ 2 5 2
- 1 4 3
输出样例:
51
48
39
42
样例解释:
| 修改 | f(1) | f(2) | f(3) | f(4) | f(5) | 结果 |
|---|---|---|---|---|---|---|
| + 1 3 1 | 3 | 2 | 1 | 4 | 5 | 51 |
| + 1 4 3 | 3 | 2 | 4 | 1 | 5 | 48 |
| + 2 5 2 | 3 | 5 | 4 | 1 | 2 | 39 |
| - 1 4 3 | 3 | 5 | 1 | 4 | 2 | 42 |
//额这道题难点就是怎么建立传送门,手动模拟一下就会发现每条路交换后缀的话答案是一样的
//其实我也不是很会,参考网上代码使用splay,详细的可以去搜搜看
#include<bits/stdc++.h>
using namespace std;
const int MAXN = 1e5 + 10; // 最大节点数
const int INF = 1e9 + 10; // 一个大的哨兵值
#define PII pair<int, int>
// 旋转树的节点结构体
struct Node {
int children[2], value, parent; // children[0]是左孩子,children[1]是右孩子,value是值,parent是父节点
int size; // 以该节点为根的子树大小
void init(int _value, int _parent) { value = _value; parent = _parent; size = 1; }
} tree[MAXN << 2]; // 开四倍大小,因为要加两个哨兵,每个查询要加两个点
#define LEFT_CHILD(node) tree[node].children[0]
#define RIGHT_CHILD(node) tree[node].children[1]
int n, m;
int root[MAXN], idx;
vector<vector<int>> version;
vector<vector<int>> binaryTree;
void pushup(int node) {
tree[node].size = tree[LEFT_CHILD(node)].size + tree[RIGHT_CHILD(node)].size + 1;
}
void rotate(int node) {
int parent = tree[node].parent, grandparent = tree[parent].parent;
int isRightChild = (tree[parent].children[1] == node);
tree[grandparent].children[tree[grandparent].children[1] == parent] = node;
tree[node].parent = grandparent;
tree[parent].children[isRightChild] = tree[node].children[isRightChild ^ 1];
tree[tree[node].children[isRightChild ^ 1]].parent = parent;
tree[node].children[isRightChild ^ 1] = parent;
tree[parent].parent = node;
pushup(parent);
pushup(node);
}
void splay(int node, int goalParent, int treeId) {
while (tree[node].parent != goalParent) {
int parent = tree[node].parent, grandparent = tree[parent].parent;
if (grandparent != goalParent) {
if ((tree[grandparent].children[0] == parent) == (tree[parent].children[0] == node)) rotate(parent);
else rotate(node);
}
rotate(node);
}
if (!goalParent) root[treeId] = node;
}
int build(int left, int right, int parent, int treeId) {
int mid = (left + right) >> 1;
int u = ++idx;
tree[u].init(treeId, parent);
version[treeId][mid] = u; // 建树时保存该点
if (left < mid) LEFT_CHILD(u) = build(left, mid - 1, u, treeId);
if (right > mid) RIGHT_CHILD(u) = build(mid + 1, right, u, treeId);
pushup(u);
return u;
}
int get_kth(int k, int node) {
while (node) {
if (tree[LEFT_CHILD(node)].size >= k) node = LEFT_CHILD(node);
else if (tree[LEFT_CHILD(node)].size + 1 == k) return tree[node].value;
else {
k -= tree[LEFT_CHILD(node)].size + 1;
node = RIGHT_CHILD(node);
}
}
return -1;
}
struct Query {
char operation;
int x1, x2, y;
};
int main() {
cin >> n >> m;
binaryTree.resize(n + 1);
// 初始化每个点的哨兵
for (int i = 1; i <= n; i++) {
binaryTree[i].push_back(0);
binaryTree[i].push_back(INF);
}
vector<Query> queries(m);
for (auto &[operation, x1, x2, y] : queries) {
cin >> operation >> x1 >> x2 >> y;
binaryTree[x1].push_back(y);
binaryTree[x2].push_back(y);
}
// 离散化
for (int i = 1; i <= n; i++) {
sort(binaryTree[i].begin(), binaryTree[i].end());
binaryTree[i].erase(unique(binaryTree[i].begin(), binaryTree[i].end()), binaryTree[i].end());
}
version = binaryTree; // 暂时将version设为binaryTree,后面建树时重新赋值
// 建树
for (int i = 1; i <= n; i++) {
root[i] = build(0, binaryTree[i].size() - 1, 0, i);
}
long long result = 0;
for (int i = 1; i <= n; i++)
result += 1ll * i * i; // 初始化答案
for (auto [operation, x1, x2, y] : queries) { // 对每个查询进行处理,交换后缀并更新答案
int pos1 = lower_bound(binaryTree[x1].begin(), binaryTree[x1].end(), y) - binaryTree[x1].begin();
int pos2 = lower_bound(binaryTree[x2].begin(), binaryTree[x2].end(), y) - binaryTree[x2].begin();
int node1 = version[x1][pos1], node2 = version[x2][pos2];
splay(node1, 0, get_kth(1, node1));
splay(node2, 0, get_kth(1, node2));
pushup(node1);
pushup(node2);
tree[RIGHT_CHILD(node1)].parent = node2;
tree[RIGHT_CHILD(node2)].parent = node1;
swap(RIGHT_CHILD(node1), RIGHT_CHILD(node2));
pushup(node1);
pushup(node2);
int start1 = get_kth(1, node1), end1 = get_kth(tree[node1].size, node1);
int start2 = get_kth(1, node2), end2 = get_kth(tree[node2].size, node2);
result += 1ll * start1 * end1 + 1ll * start2 * end2;
result -= 1ll * start1 * end2 + 1ll * start2 * end1;
cout << result << "\n";
}
}
L3-027 可怜的复杂度
分数 80
全屏浏览
切换布局
作者 吉如一
单位 北京大学
可怜有一个数组 A,定义它的复杂度 c(A) 等于它本质不同的子区间个数。举例来说,c([1,1,1])=3,因为 [1,1,1] 只有 3 个本质不同的子区间 [1]、[1,1] 和 [1,1,1];而 c([1,2,1])=5,它包含 5 个本质不同的子区间 [1]、[2]、[1,2]、[2,1]、[1,2,1]。
可怜打算出一道和复杂度相关的题目。众所周知,引入随机性往往可以让一个简单的题目脱胎换骨。现在,可怜手上有一个长度为 n 的正整数数组 x 和一个正整数 m。接着,可怜会独立地随机产生 n 个 [1,m] 中的随机整数 yi,并把 xi 修改为 mxi+yi。
显然,一共有 N=mn 种可能的结果数组。现在,可怜想让你求出这 N 个数组的复杂度的和。
输入格式:
第一行给出一个整数 t (1≤t≤5) 表示数据组数。
对于每组数据,第一行输入两个整数 n 和 m (1≤n≤100,1≤m≤109),第二行是 n 个空格隔开的整数表示数组 x 的初始值 (1≤xi≤109)。
输出格式:
对于每组数据,输出一行一个整数表示答案。答案可能很大,你只需要输出对 998244353 取模后的结果。
输入样例:
4
3 2
1 1 1
3 2
1 2 1
5 2
1 2 1 2 1
10 2
80582987 187267045 80582987 187267045 80582987 187267045 80582987 187267045 80582987 187267045
输出样例:
36
44
404
44616//我靠这道题真的操蛋,为什么会内存超限啊,先讲下思路
//容斥原理肯定跑不了
#include <iostream>
#include <vector>
#include <unordered_set>
#include <unordered_map>
#include <string>
using namespace std;
const int MOD = 998244353;
// 计算所有本质不同子区间的数量
int countDistinctSubarrays(const vector<int>& arr) {
unordered_set<int> uniqueSubarrays;
int n = arr.size();
for (int i = 0; i < n; ++i) {
int subarray=0;
for (int j = i; j < n; ++j) {
subarray = subarray*10+arr[j];
uniqueSubarrays.insert(subarray);
}
}
return uniqueSubarrays.size();
}
int main() {
int t;
cin >> t;
while (t--) {
int n, m;
cin >> n >> m;
vector<int> x(n);
for (int i = 0; i < n; ++i) {
cin >> x[i];
}
unordered_map<string, int> dp;
dp[""] = 1; // 初始状态
long long totalComplexity = 0;
for (int i = 0; i < n; ++i) {
unordered_map<string, int> newDp;
for (const auto& [key, value] : dp) {
for (int j = 1; j <= m; ++j) {
string newKey = key + to_string(x[i] * m + j) + ",";
newDp[newKey] = (newDp[newKey] + value) % MOD;
}
}
dp.swap(newDp);
}
for (const auto& [key, value] : dp) {
vector<int> arr;
size_t start = 0;
size_t end = key.find(",");
while (end != string::npos) {
arr.push_back(stoi(key.substr(start, end - start)));
start = end + 1;
end = key.find(",", start);
}
totalComplexity = (totalComplexity + (long long)countDistinctSubarrays(arr) * value) % MOD;
}
cout << totalComplexity << endl;
}
return 0;
}
注意:这道题同样只能过第一个点,后面都是内存超限了,额我觉得算法上应该没问题,大家可以不用map和set储存优化一下,太菜了不会。
L3-028 森森旅游
分数 60
全屏浏览
切换布局
作者 DAI, Longao
单位 杭州百腾教育科技有限公司
好久没出去旅游啦!森森决定去 Z 省旅游一下。
Z 省有 n 座城市(从 1 到 n 编号)以及 m 条连接两座城市的有向旅行线路(例如自驾、长途汽车、火车、飞机、轮船等),每次经过一条旅行线路时都需要支付该线路的费用(但这个收费标准可能不止一种,例如车票跟机票一般不是一个价格)。
Z 省为了鼓励大家在省内多逛逛,推出了旅游金计划:在 i 号城市可以用 1 元现金兑换 ai 元旅游金(只要现金足够,可以无限次兑换)。城市间的交通即可以使用现金支付路费,也可以用旅游金支付。具体来说,当通过第 j 条旅行线路时,可以用 cj 元现金或 dj 元旅游金支付路费。注意: 每次只能选择一种支付方式,不可同时使用现金和旅游金混合支付。但对于不同的线路,旅客可以自由选择不同的支付方式。
森森决定从 1 号城市出发,到 n 号城市去。他打算在出发前准备一些现金,并在途中的某个城市将剩余现金 全部 换成旅游金后继续旅游,直到到达 n 号城市为止。当然,他也可以选择在 1 号城市就兑换旅游金,或全部使用现金完成旅程。
Z 省政府会根据每个城市参与活动的情况调整汇率(即调整在某个城市 1 元现金能换多少旅游金)。现在你需要帮助森森计算一下,在每次调整之后最少需要携带多少现金才能完成他的旅程。
输入格式:
输入在第一行给出三个整数 n,m 与 q(1≤n≤105,1≤m≤2×105,1≤q≤105),依次表示城市的数量、旅行线路的数量以及汇率调整的次数。
接下来 m 行,每行给出四个整数 u,v,c 与 d(1≤u,v≤n,1≤c,d≤109),表示一条从 u 号城市通向 v 号城市的有向旅行线路。每次通过该线路需要支付 c 元现金或 d 元旅游金。数字间以空格分隔。输入保证从 1 号城市出发,一定可以通过若干条线路到达 n 号城市,但两城市间的旅行线路可能不止一条,对应不同的收费标准;也允许在城市内部游玩(即 u 和 v 相同)。
接下来的一行输入 n 个整数 a1,a2,⋯,an(1≤ai≤109),其中 ai 表示一开始在 i 号城市能用 1 元现金兑换 ai 个旅游金。数字间以空格分隔。
接下来 q 行描述汇率的调整。第 i 行输入两个整数 xi 与 ai′(1≤xi≤n,1≤ai′≤109),表示第 i 次汇率调整后,xi 号城市能用 1 元现金兑换 ai′ 个旅游金,而其它城市旅游金汇率不变。请注意:每次汇率调整都是在上一次汇率调整的基础上进行的。
输出格式:
对每一次汇率调整,在对应的一行中输出调整后森森至少需要准备多少现金,才能按他的计划从 1 号城市旅行到 n 号城市。
再次提醒:如果森森决定在途中的某个城市兑换旅游金,那么他必须将剩余现金全部、一次性兑换,剩下的旅途将完全使用旅游金支付。
输入样例:
6 11 3
1 2 3 5
1 3 8 4
2 4 4 6
3 1 8 6
1 3 10 8
2 3 2 8
3 4 5 3
3 5 10 7
3 3 2 3
4 6 10 12
5 6 10 6
3 4 5 2 5 100
1 2
2 1
1 17
输出样例:
8
8
1
样例解释:
对于第一次汇率调整,森森可以沿着 1→2→4→6 的线路旅行,并在 2 号城市兑换旅游金;
对于第二次汇率调整,森森可以沿着 1→2→3→4→6 的线路旅行,并在 3 号城市兑换旅游金;
对于第三次汇率调整,森森可以沿着 1→3→5→6 的线路旅行,并在 1 号城市兑换旅游金。
//这道题很长啊我们直接讲人话
//就是说有一个图,这个图里面两个结点之间可能有不止一条路线,也可能有环
//问从1号点到指定点所需要的最少现金,中间可以根据汇率将现金转化为旅游币
//这道题的存储方式就是接邻表,用的算法应该是迪杰斯特拉
//最主要的问题是怎么处理汇率,就是建图额然后建个反向图
//枚举每个点作为汇率啊,然后用优先队列优化一下不然会超时
#include<bits/stdc++.h>
using namespace std;
const int N=1e5+5;
const int M=2e5+10;//为了空间足够需要开辟两倍
typedef long long ll;
typedef pair<ll,int> node; //第一个也就是dis,第二个是编号
struct Graph{
int addres=0;
int head[N]={0};
int ver[M]={0};
int next[M]={0};
int val[M]={0};
//添加函数
void add(int u,int v,int w){
ver[++addres]=v;
val[addres]=w;
next[addres]=head[u];
head[u]=addres;
}
ll dis[N]={0};
bool visit[N]={0};//也就是false
void dijk(int st){
priority_queue< node, vector<node>, greater<node> >q;//小顶堆
memset(dis, 9999999, sizeof(dis));
q.emplace(0,st);//传入堆
dis[st]=0;
while(!q.empty()){
int u=q.top().second;
q.pop();
if(visit[u])//已经访问过了
continue;
visit[u]=true;
//更新相邻结点
for(int i=head[u];i!=0;i=next[i]){
int v=ver[i];
if(dis[u]+val[i]<dis[v]){
dis[v]=dis[u]+val[i];
q.emplace(dis[v],v);
}
}
}
}
}G1,G2; //一个是正向图,用来计算先进;另一个是反向图用来计算旅游币
ll a[N]; //用来储存每个点的汇率
int main(){
int n,m,Q;
cin>>n>>m>>Q;
for(int i=1;i<=m;i++){
int u,v,c,d;
cin>>u>>v>>c>>d;
G1.add(u,v,c);
G2.add(v,u,d);
}
G1.dijk(1);//从编号1开始
G2.dijk(n);
multiset<ll> Set;//我们要这个里面的数据绝对有序,然后只拿第一个就行了
for(int i=1;i<=n;i++) {
cin>>a[i];
if (G1.visit[i] && G2.visit[i]) //这个是我发现md这个题目竟然不保证所有点连通
Set.insert(G1.dis[i] + ceil((double)G2.dis[i] / a[i]));//全部转成现金
}
for(int i=1;i<=Q;i++){
int x,y;
cin>>x>>y;
if (G1.visit[x] && G2.visit[x]) {
Set.erase(Set.find(G1.dis[x] + ceil((double)G2.dis[x] / a[x]))); //删除原本的
a[x]=y;
Set.insert(G1.dis[x] + ceil((double)G2.dis[x] / a[x])); //加入新的,记住一定要删
}
printf("%lld\n", *Set.begin());
}
}
L3-029 还原文件
分数 80
全屏浏览
切换布局
作者 陈越
单位 浙江大学
一份重要文件被撕成两半,其中一半还被送进了碎纸机。我们将碎纸机里找到的纸条进行编号,如图 1 所示。然后根据断口的折线形状跟没有切碎的半张纸进行匹配,最后还原成图 2 的样子。要求你输出还原后纸条的正确拼接顺序。
图1 纸条编号
图2 还原结果
输入格式:
输入首先在第一行中给出一个正整数 N(1<N≤105),为没有切碎的半张纸上断口折线角点的个数;随后一行给出从左到右 N 个折线角点的高度值(均为不超过 100 的非负整数)。
随后一行给出一个正整数 M(≤100),为碎纸机里的纸条数量。接下去有 M 行,其中第 i 行给出编号为 i(1≤i≤M)的纸条的断口信息,格式为:
K h[1] h[2] ... h[K]
其中 K 是断口折线角点的个数(不超过 104+1),后面是从左到右 K 个折线角点的高度值。为简单起见,这个“高度”跟没有切碎的半张纸上断口折线角点的高度是一致的。
输出格式:
在一行中输出还原后纸条的正确拼接顺序。纸条编号间以一个空格分隔,行首尾不得有多余空格。
题目数据保证存在唯一解。
输入样例:
17
95 70 80 97 97 68 58 58 80 72 88 81 81 68 68 60 80
6
4 68 58 58 80
3 81 68 68
3 95 70 80
3 68 60 80
5 80 72 88 81 81
4 80 97 97 68
输出样例:
3 6 1 5 2 4//爆掉了,还是要搜索
#include<iostream>
#include<vector>
using namespace std;
const int N=100005;
int n,m;
int a[N],ans[105];
int p;
int f=0;
vector<int> b[105];
bool st[105];//判断是否已经额使用过
void dfs(int s){
if(s==n-1){
for(int i=0;i<p;++i){
if(i!=p-1)
cout<<ans[i]<<" ";
else
cout<<ans[i];
}
f=1;
return;
}
for(int i=1;i<=m;++i){
if(st[i])
continue;
bool flag=true;
for(int j=0;j<b[i].size();++j){
if(a[s+j]!=b[i][j]){
flag=false;
break;
}
}
if(flag){
ans[p++]=i;//如果匹配
st[i]=true;
dfs(s+b[i].size()-1);
p--;//需要回溯,因为可能存在顺序问题,一个碎纸片在多个位置都能匹配,但是只有它在某一个位置才能保证全局都能匹配
st[i]=false;
if(f==1)
return;//减少运行时间
}
}
}
int main(){
cin>>n;
for(int i=0;i<n;i++)
cin>>a[i];
cin>>m;
for(int i=1;i<=m;i++){
int k;
cin>>k;
for(int j=0;j<k;j++){
int x;
cin>>x;
b[i].push_back(x);
}
}
dfs(0);
return 0;
}
L3-030 可怜的简单题
分数 80
全屏浏览
切换布局
作者 吉如一
单位 北京大学
九条可怜去年出了一道题,导致一众参赛高手惨遭团灭。今年她出了一道简单题 —— 打算按照如下的方式生成一个随机的整数数列 A:
-
最开始,数列 A 为空。
-
可怜会从区间 [1,n] 中等概率随机一个整数 i 加入到数列 A 中。
-
如果不存在一个大于 1 的正整数 w,满足 A 中所有元素都是 w 的倍数,数组 A 将会作为随机生成的结果返回。否则,可怜将会返回第二步,继续增加 A 的长度。
现在,可怜告诉了你数列 n 的值,她希望你计算返回的数列 A 的期望长度。
输入格式:
输入一行两个整数 n,p (1≤n≤1011,n<p≤1012),p 是一个质数。
输出格式:
在一行中输出一个整数,表示答案对 p 取模的值。具体来说,假设答案的最简分数表示为 yx,你需要输出最小的非负整数 z 满足 y×z≡x mod p。
输入样例 1:
2 998244353
输出样例 1:
2
输入样例 2:
100000000 998244353
输出样例 2:
3056898//网上用的是莫比乌斯反演和杜教筛,数论这一块我确实不是很会啊我就直接跟这写了
#include <bits/stdc++.h>
#define int long long // 使用long long类型来处理大数
using namespace std;
const int N = 2.2e7 + 5; // 常量N,用于筛法的上限
vector<int> primes;
vector<int> mobius(N, 0), sum(N, 0);
vector<bool> is_composite(N, false); // 标记是否为合数
void sieve(int n, int mod) {
mobius[1] = 1;
for (int i = 2; i <= n; i++) {
if (!is_composite[i]) {
primes.push_back(i);
mobius[i] = -1;
}
//这边类型一定要注意啊,之前没注意一直报错,要把size_t作为类型不然不能比较
for (size_t j = 0; j < primes.size() && i * primes[j] <= n; j++) {
int t = i * primes[j];
is_composite[t] = true;
if (i % primes[j] == 0) {
mobius[t] = 0;
break;
}
mobius[t] = -mobius[i];
}
}
for (int i = 1; i <= n; i++) {
sum[i] = (sum[i - 1] + mobius[i] + mod) % mod;
}
}
// 快速乘法,用于处理大数取模
int qmul(int a, int b, int mod) {
return (__int128)a * b % mod;
}
// 快速幂,用于计算模逆元
int qmi(int a, int b, int mod) {
int res = 1;
while (b) {
if (b & 1) res = qmul(res, a, mod);
a = qmul(a, a, mod);
b >>= 1;
}
return res;
}
// 使用记忆化的递归函数计算莫比乌斯前缀和
unordered_map<int, int> memo;
int Sum(int n, int mod) {
if (n < N) return sum[n];
if (memo.count(n)) return memo[n];
int res = 1;
for (int l = 2, r; l <= n; l = r + 1) {
r = n / (n / l);
res = (res - qmul(r - l + 1, Sum(n / l, mod), mod) + mod) % mod;
}
return memo[n] = res;
}
signed main() {
// 读取输入的n和mod
int n, mod;
cin >> n >> mod;
// 调用筛法计算莫比乌斯函数
sieve(N - 1, mod);
// 计算期望长度
int result = 1;
for (int l = 2, r; l <= n; l = r + 1) {
r = n / (n / l);
int t = qmul(n / l, qmi(n - n / l, mod - 2, mod), mod);
result = (result - qmul(Sum(r, mod) - Sum(l - 1, mod), t, mod) + mod) % mod;
}
// 输出结果
cout << result << endl;
}
L3-031 千手观音
分数 60
全屏浏览
切换布局
作者 陈越
单位 浙江大学

人类喜欢用 10 进制,大概是因为人类有一双手 10 根手指用于计数。于是在千手观音的世界里,数字都是 10 000 进制的,因为每位观音有 1 000 双手 ……
千手观音们的每一根手指都对应一个符号(但是观音世界里的符号太难画了,我们暂且用小写英文字母串来代表),就好像人类用自己的 10 根手指对应 0 到 9 这 10 个数字。同样的,就像人类把这 10 个数字排列起来表示更大的数字一样,ta们也把这些名字排列起来表示更大的数字,并且也遵循左边高位右边低位的规则,相邻名字间用一个点 . 分隔,例如 pat.pta.cn 表示千手观音世界里的一个 3 位数。
人类不知道这些符号代表的数字的大小。不过幸运的是,人类发现了千手观音们留下的一串数字,并且有理由相信,这串数字是从小到大有序的!于是你的任务来了:请你根据这串有序的数字,推导出千手观音每只手代表的符号的相对顺序。
注意:有可能无法根据这串数字得到全部的顺序,你只要尽量推出能得到的结果就好了。当若干根手指之间的相对顺序无法确定时,就暂且按它们的英文字典序升序排列。例如给定下面几个数字:
pat
cn
lao.cn
lao.oms
pta.lao
pta.pat
cn.pat
我们首先可以根据前两个数字推断 pat < cn;根据左边高位的顺序可以推断 lao < pta < cn;再根据高位相等时低位的顺序,可以推断出 cn < oms,lao < pat。综上我们得到两种可能的顺序:lao < pat < pta < cn < oms;或者 lao < pta < pat < cn < oms,即 pat 和 pta 之间的相对顺序无法确定,这时我们按字典序排列,得到 lao < pat < pta < cn < oms。
输入格式:
输入第一行给出一个正整数 N (≤105),为千手观音留下的数字的个数。随后 N 行,每行给出一个千手观音留下的数字,不超过 10 位数,每一位的符号用不超过 3 个小写英文字母表示,相邻两符号之间用 . 分隔。
我们假设给出的数字顺序在千手观音的世界里是严格递增的。题目保证数字是 104 进制的,即符号的种类肯定不超过 104 种。
输出格式:
在一行中按大小递增序输出符号。当若干根手指之间的相对顺序无法确定时,按它们的英文字典序升序排列。符号间仍然用 . 分隔。
输入样例:
7
pat
cn
lao.cn
lao.oms
pta.lao
pta.pat
cn.pat
输出样例:
lao.pat.pta.cn.oms//这道题多数采用链式向前星的方式
//我不是很会啊也比较麻烦,我就直接拓扑排序+优先队列了
//主要思路就是先用拓扑排序搞出可以确定地大小,然后逐一拿出来放到优先队列里排字符串大小
//我靠超时了,我看看怎么个事
//我靠找到问题了在unordered_map上,这个比map快很多,有点极限
#include <bits/stdc++.h>
using namespace std;
const int N = 1e5 + 5, M = 2e6 + 5;
int address, head[N], ver[M], nxt[M];
//图的储存
void add(int u, int v) {
ver[++address] = v;
nxt[address] = head[u];
head[u] = address;
}
unordered_map<string, int> s_i; //字符串对应编号
unordered_map<int, string> i_s; //编号对应字符串
int n, strtot;
int ind[N];
typedef pair<string, int> node;
vector<string> ans; //用来储存最后的排序
int main() {
cin>>n;
vector<string> pre, now; //pre是前面的字符串,now是当前的字符串,里面储存的是子串
for(int i = 1; i <= n; i++) {
string str;
cin >> str;
for(int p = 0; p < str.size(); p++) {
string nows;
while(p < str.size() && str[p] != '.') nows += str[p++];
if(s_i.find(nows) == s_i.end()) {
s_i[nows] = ++strtot;
i_s[strtot] = nows;
}
now.push_back(nows);
}
if(pre.size() == now.size()) {
int p = 0;
while(pre[p] == now[p])
p++;
add(s_i[pre[p]], s_i[now[p]]);
ind[s_i[now[p]]]++; //入度增加
}
pre=now; //覆盖赋值
now.clear();
}
//考虑到最后的排序使用优先队列
//会优先根据node中的string进行排序,然后根据第二个编号也就是我们定义的大小来排序
//由于在外面我们已经进行了一个拓扑图排序,一次在这个里面优先比较字符串大小
priority_queue<node, vector<node>, greater<node>> q;
for(auto& [str, id] : s_i) {
if(ind[id]==0)
q.emplace(str, id);
}
while(!q.empty()) {
ans.push_back(q.top().first);
int u = q.top().second;
q.pop();
for(int i = head[u]; i; i = nxt[i]) {
int v = ver[i];
ind[v]--;
if(!ind[v])
q.emplace(i_s[v], v);
}
}
cout << ans[0];
for(int i = 1; i < ans.size(); i++)
cout << "." << ans[i];
return 0;
}
L3-032 关于深度优先搜索和逆序对的题应该不会很难吧这件事
分数 80
全屏浏览
切换布局
作者 DAI, Longao
单位 杭州百腾教育科技有限公司
背景知识
深度优先搜索与 DFS 序
深度优先搜索算法(DFS)是一种用于遍历或搜索树或图的算法。以下伪代码描述了在树 T 上进行深度优先搜索的过程:
procedure DFS(T, u, L) // T 是被深度优先搜索的树
// u 是当前搜索的节点
// L 是一个链表,保存了所有节点被第一次访问的顺序
append u to L // 将节点 u 添加到链表 L 的末尾
for v in u.children do // 枚举节点 u 的所有子节点 v
DFS(T, v) // 递归搜索节点 v
令 r 为树 T 的根,调用 DFS(T, r, L) 即可完成对 T 的深度优先搜索,保存在链表 L 中的排列被称为 DFS 序。相信聪明的你已经发现了,如果枚举子节点的顺序不同,最终得到的 DFS 序也会不同。
逆序对
给定一个长度为 n 的整数序列 a1,a2,⋯,an,该序列的逆序对数量是同时满足以下条件的有序数对 (i,j) 的数量:
- 1≤i<j≤n;
- ai>aj。
问题求解
给定一棵 n 个节点的树,其中节点 r 为根。求该树所有可能的 DFS 序中逆序对数量之和。
输入格式
第一行输入两个整数 n,r(2≤n≤3×105,1≤r≤n)表示树的大小与根节点。
对于接下来的 (n−1) 行,第 i 行输入两个整数 ui 与 vi(1≤ui,vi≤n),表示树上有一条边连接节点 ui 与 vi。
输出格式
输出一行一个整数,表示该树所有可能的 DFS 序中逆序对数量之和。由于答案可能很大,请对 109+7 取模后输出。
样例输入 1
5 3
1 5
2 5
3 5
4 3
样例输出 1
24
样例输入 2
10 5
10 2
2 5
10 7
7 1
7 9
4 2
3 10
10 8
3 6
样例输出 2
516
样例解释
下图展示了样例 1 中的树。
该树共有 4 种可能的 DFS 序:
- {3,4,5,1,2},有 6 个逆序对;
- {3,4,5,2,1},有 7 个逆序对;
- {3,5,1,2,4},有 5 个逆序对;
- {3,5,2,1,4},有 6 个逆序对。
因此答案为 6+7+5+6=24。
//这道题本质上不难,虽然说是一棵树,但实际上可以用图来储存
//额树的话实际上就是单向图
//然后dfs搜一下然后存储路径就行了
//其实不需要管怎么排,把父节点放在树状数组里面,每次遍历就更新一遍就好了
//逆序对就直接树状数组就好了
#include<iostream>
#include<cstring>
const int MOD=1e9+7;
using namespace std;
struct node{//链表快速写法,正好看过
int to,nex;
}edge[600010];
int head[300010];
int cnt;
int tree[300010];
int dep[300010];
int siz[300010];
long long sum=1;
long long n,ans;
int lowbit(int x){
return x&-x;
}
void add(int x,int k){ //用来构造树状数组
for(int i=x;i<=n;i+=lowbit(i))
tree[i]+=k;
}
int find(int x){ //区间查询
int ans=0;
for(int i=x;i>0;i-=lowbit(i))
ans+=tree[i];
return ans;
}
void addedge(int x,int y){ //邻接图
edge[++cnt].to=y;
edge[cnt].nex=head[x];
head[x]=cnt;
}
void dfs(int p,int f){
siz[p]=1;
dep[p]=dep[f]+1;
//第一类关系,也就是有先祖关系
long long tmp=find(n-p+1);
long long x=1;
long long yy=1;
ans=(ans+tmp)%MOD;
add(n-p+1,1);
for(int i=head[p];i!=-1;i=edge[i].nex){
int y=edge[i].to;
if(y==f)
continue;
x=x*yy%MOD; yy++;
dfs(y,p);
siz[p]+=siz[y];
}
if(x>1)
sum=sum*x%MOD;
add(n-p+1,-1);
}
int main(){
long long root,x,y;
cin>>n>>root;
memset(head,-1,sizeof(head));
for(int i=1;i<n;i++){
cin>>x>>y;
addedge(x,y);
addedge(y,x);
}
dfs(root,0);
ans=ans*sum%MOD;
for(int i=1;i<=n;i++){
x=n-dep[i]-siz[i]+1;
//这里应该是1/4但是好像直接除4中间会有答案错,看了网上的方法
ans=(ans+x*sum%MOD*500000004%MOD*500000004%MOD)%MOD;
}
cout<<ans;
}
L3-033 教科书般的亵渎
分数 80
全屏浏览
切换布局
作者 吉如一
单位 北京大学
九条可怜最近在玩一款卡牌游戏。在每一局游戏中,可怜都要使用抽到的卡牌来消灭一些敌人。每一名敌人都有一个初始血量,而当血量降低到 0 及以下的时候,这名敌人就会立即被消灭并从场上消失。
现在,可怜面前有 n 个敌人,其中第 i 名敌人的血量是 ai,而可怜手上只有如下两张手牌:
-
如果场上还有敌人,等概率随机选中一个敌人并对它造成一点伤害(即血量减 1),重复 K 次。
-
对所有敌人造成一点伤害,重复该效果直到没有新的敌人被消灭。
下面是这两张手牌效果的一些示例:
- 假设存在两名敌人,他们的血量分别是 1,2 且 K=2。那么在可怜打出第一张手牌后,可能会发生如下情况:
- 第一轮中,两名敌人各有 0.5 的概率被选中。假设第一名敌人被选中,那么它会被造成一点伤害。这时它的血量变成了 0,因此它被消灭并消失了。
- 第二轮中,因为场上只剩下了第二名敌人,所以它一定会被选中并被造成一点伤害。这时它剩下的血量为 1。
- 同样假设存在两名敌人且血量分别为 1,2。那么在可怜打出第二张手牌后,会发生如下情况:
- 第一轮中,所有敌人被造成了一点伤害。这时第一名敌人被消灭了,因此卡牌效果会被重复一遍。
- 第二轮中,所有敌人(此时只剩下第二名敌人了)被造成了一点伤害。这时第二名敌人也被消灭了,因此卡牌效果会被再重复一遍。
- 第三轮中,所有敌人(此时没有敌人剩下了)被造成了一点伤害。因为没有新的敌人被消灭了,所以卡牌效果结束。
- 如果面对的是四名血量分别为 1,2,2,4 的敌人,那么在可怜打出第二张手牌后,只有第四名敌人还会存活,且它的剩余血量为 1。
现在,可怜先打出了第一张手牌,再打出了第二张手牌。她发现,在第一张手牌效果结束后,没有任何一名敌人被消灭,但是在第二张手牌的效果结束后,所有敌人都被消灭了。
可怜想让你计算一下这种情况发生的概率是多少。
输入格式:
第一行输入两个整数 n,K(1≤n,K≤50),分别表示敌人的数量以及第一张卡牌效果的发动次数。
第二行输入 n 个由空格隔开的整数 ai(1≤ai≤50),表示每个敌人的初始血量。
输出格式:
在一行中输出一个整数,表示发生概率对 998244353 取模后的结果。
具体来说,如果概率的最简分数表示为 a/b(a≥0,b≥1,gcd(a,b)=1),那么你需要输出
a×b998244351mod998244353。
输入样例 1:
3 2
2 3 3
输出样例 1:
665496236
样例解释 1:
在第一张手牌的效果结束后,三名敌人的剩余血量只可能在如下几种中:[1,3,2], [1,2,3], [2,1,3] 和 [2,3,1]。前两种发生的概率是 2/9,后两种发生的概率是 1/9。因此答案为 2/3,输出 2×3998244351mod998244353=665496236。
输入样例 2:
3 3
2 3 3
输出样例 2:
776412275
样例解释 2:
在第一张手牌的效果结束后,三名敌人的剩余血量只可能在如下几种中:[1,2,2]、[2,1,2] 和 [2,2,1]。第一种发生的概率是 2/9,后两种发生的概率是 1/9。因此答案为 4/9,输出 4×9998244351mod998244353=776412275。
输入样例 3:
5 3
1 4 4 2 5
输出样例 3:
367353922
输入样例 4:
12 12
1 2 3 4 5 6 7 8 9 10 11 12
输出样例 4:
452061016#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;
const int MOD = 998244353;
// 计算模逆元
int modInverse(int x, int mod) {
int res = 1, exp = mod - 2;
while (exp > 0) {
if (exp % 2 == 1) res = (long long)res * x % mod;
x = (long long)x * x % mod;
exp /= 2;
}
return res;
}
// 状态压缩的动态规划
int main() {
int n, K;
cin >> n >> K;
vector<int> a(n);
for (int i = 0; i < n; ++i) {
cin >> a[i];
}
// 定义dp数组,dp[k][S]表示经过k次操作后状态S的方案数
vector<vector<int>> dp(K + 1, vector<int>(1 << n, 0));
dp[0][(1 << n) - 1] = 1; // 初始状态,所有敌人都存活
// 动态规划
for (int k = 0; k < K; ++k) {
for (int S = 0; S < (1 << n); ++S) {
if (dp[k][S] == 0) continue;
for (int i = 0; i < n; ++i) {
if (S & (1 << i)) { // 如果敌人i还存活
int nextS = S & ~(1 << i); // 敌人i被击中,血量减1
dp[k + 1][nextS] = (dp[k + 1][nextS] + dp[k][S]) % MOD;
}
}
}
}
// 计算所有敌人都存活的总方案数
int totalCount = 1;
for (int i = 0; i < K; ++i) {
totalCount = (long long)totalCount * n % MOD;
}
// 计算至少一个敌人被消灭的方案数
int validCount = 0;
for (int S = 0; S < (1 << n); ++S) {
bool allAlive = true;
for (int i = 0; i < n; ++i) {
if ((S & (1 << i)) == 0 && a[i] <= K) {
allAlive = false;
break;
}
}
if (!allAlive) {
validCount = (validCount + dp[K][S]) % MOD;
}
}
// 计算最终答案
int result = (long long)validCount * modInverse(totalCount, MOD) % MOD;
cout << result << endl;
return 0;
}
这道数论题也就是纯纯骗分了,下面提供一个可行的思路,有兴趣的小伙伴可以试下 。