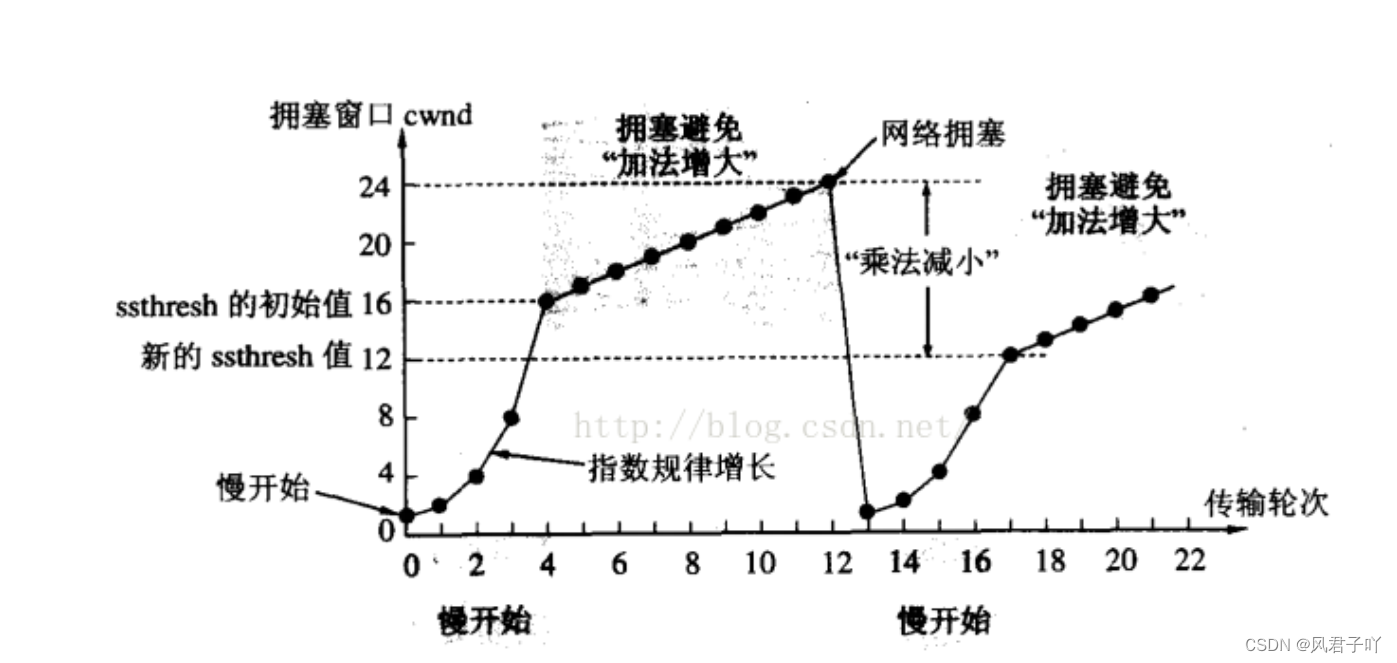
什么是杨辉三角形

本文旨在讨论普通杨辉三角形的两种实现方式：迭代法和递归法。我们不详细讲解杨辉三角形的数学问题，只研究其代码实现。
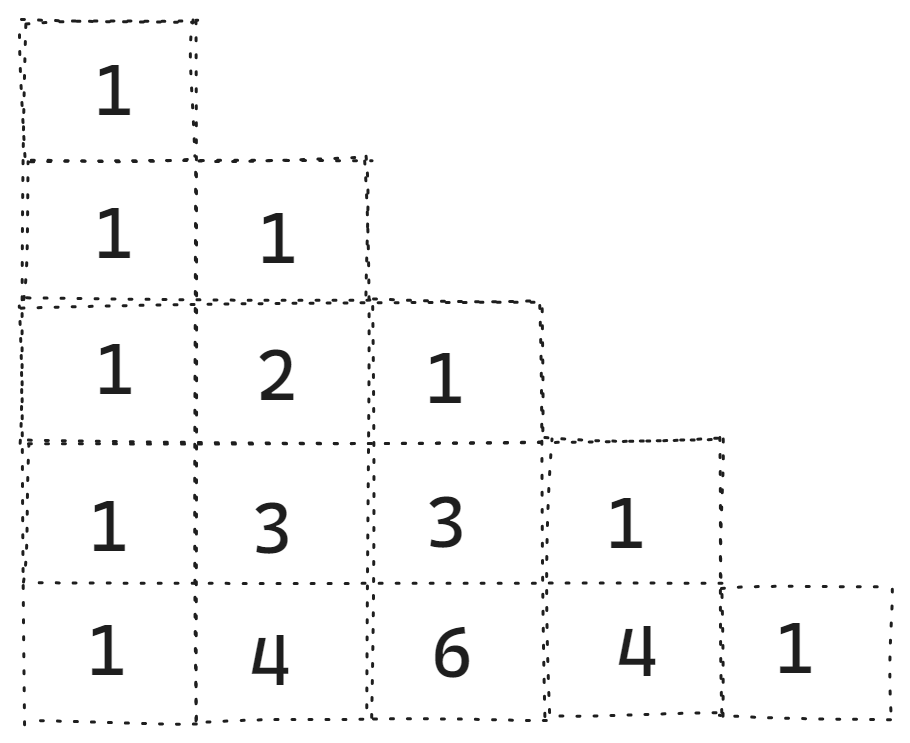
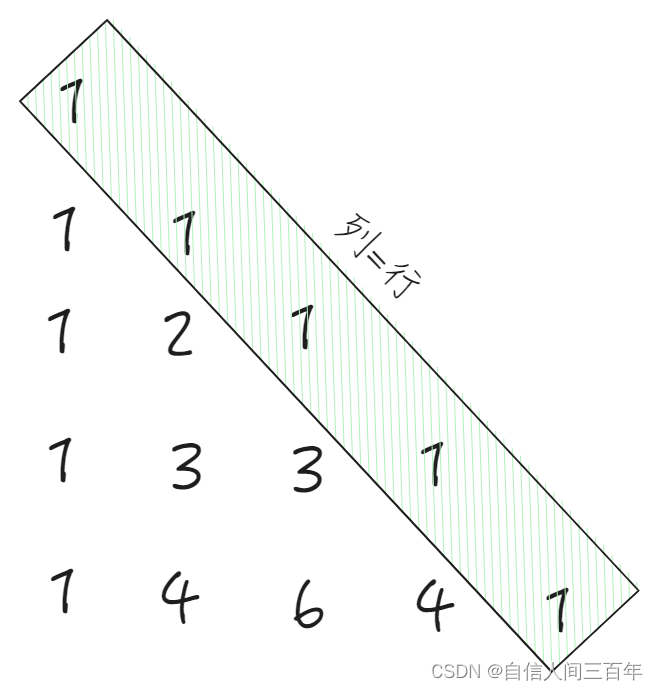
杨辉三角形大致如下图：

杨辉三角形的规律

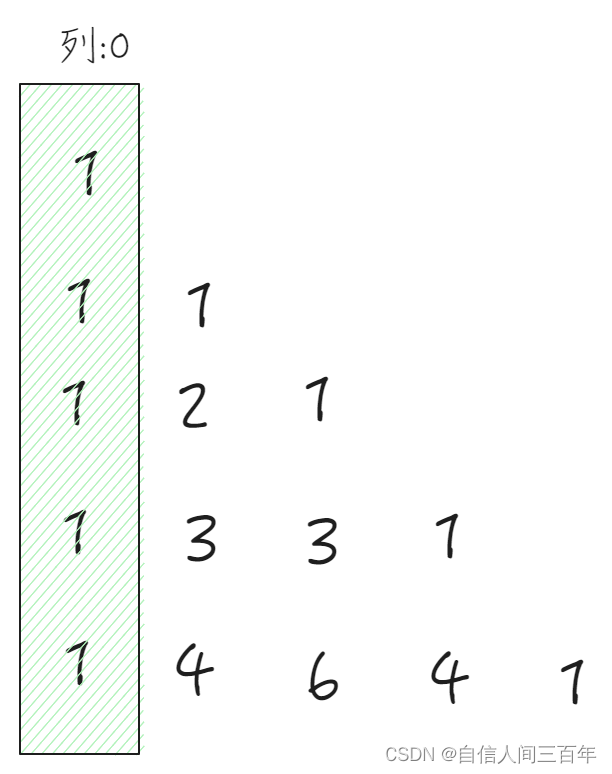
通过对杨辉三角形的图形分析，我们可以看到这几点

1. 直角三角形 :每行内的数据和和行的个数相等,例如第1行 1列，第2行有2列，第3行有3列…。

2. 第一列和斜边列值都为1: 列 = =0；结果为1，列==行， 结果1
   
   

3. 其它每个元素的结果= 上一行的前一列数据 + 上一行的当前列数据，使用数组表示： a[row][col] = a[row-1][col-1] + a[row-1][col];

迭代实现

所谓迭代实现实际上是使用循环对变量中的数据进行迭代处理。此法我们需要使用数组记录每个杨辉三角形中的数据。安装以上规律组织代码:

int[][] a = new int[10][10]; //定义数组存储杨辉三角形数据

for (int row = 0; row < a.length; row++) { //外循环表示三角形行
    for (int col = 0; col <= row; col++) {//内循环表示三角形列
        if (col == 0 || col == row) {//第一列或者三角形斜边值为1
            a[row][col] = 1;
        } else { //当前值为上一行的相邻两数和
            a[row][col] = a[row - 1][col - 1] + a[row - 1][col];
        }
    }
}
/**
 *  打印杨辉三角形
 */
for (int row = 0; row < a.length; row++) {
    for (int col = 0; col <= row; col++) {
        System.out.print(a[row][col] + "\t");
    }
    System.out.println();
}

递归实现

递归实现需要使用方法来构建递归模型。需要找出递归的终止条件和一般规律：
终止条件： col= =0 或者 col= =row 则结果为1
一般规律： f(row,col) = f(row-1, col-1) + f(row-1,col);

 public static int f(int row, int col){
        if(col==0|| row ==col) return 1;
        return f(row-1,col-1)+ f(row-1,col);
    }