前言
快排解决办法有很多种,这里我再拿出来一种前后指针版本
虽然这个版本的时间复杂度和霍尔一样,逻辑也差不多,但是实际排序过程,确实会比霍尔慢一点
快排gif
快排前后指针实现逻辑:
前后指针实现逻辑(升序):
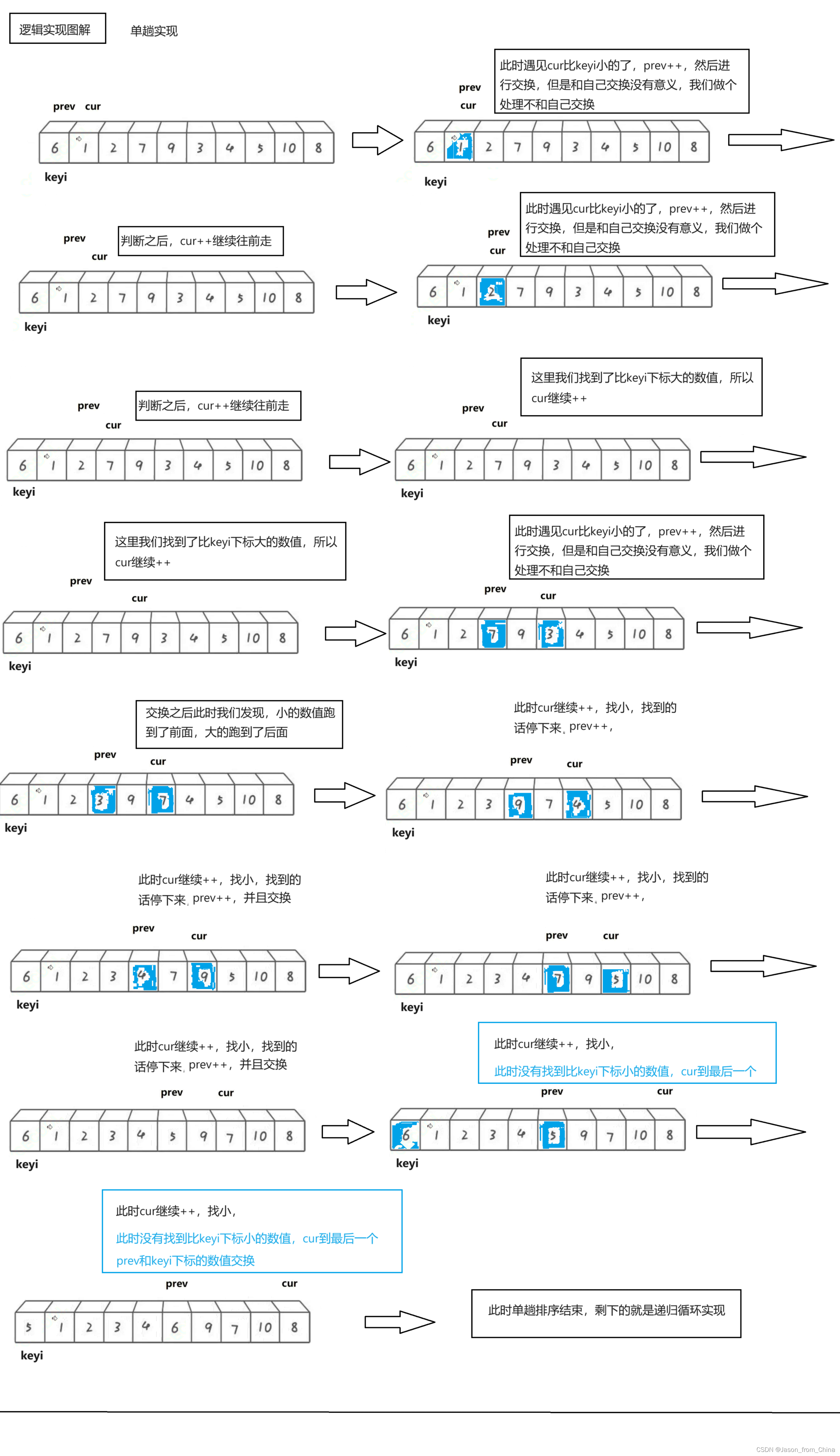
单趟排序:
1,我们使用递归来进行实现,所以我们先实现单趟排序
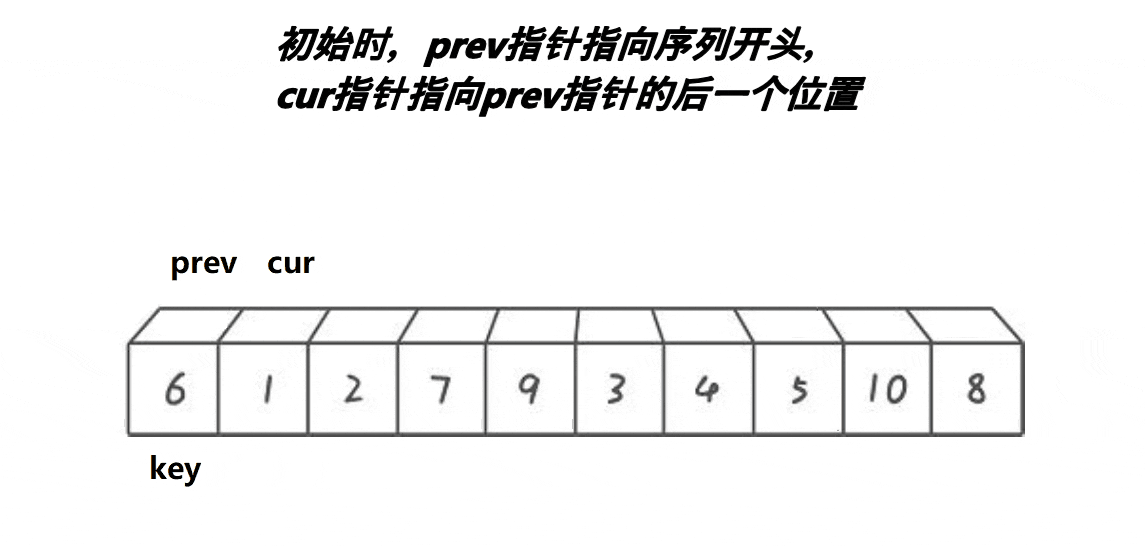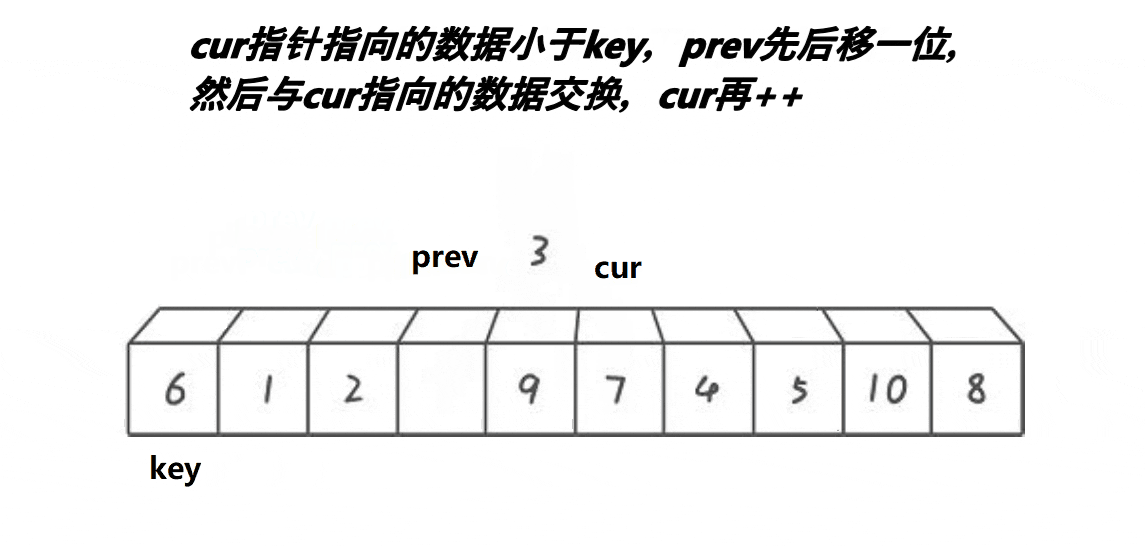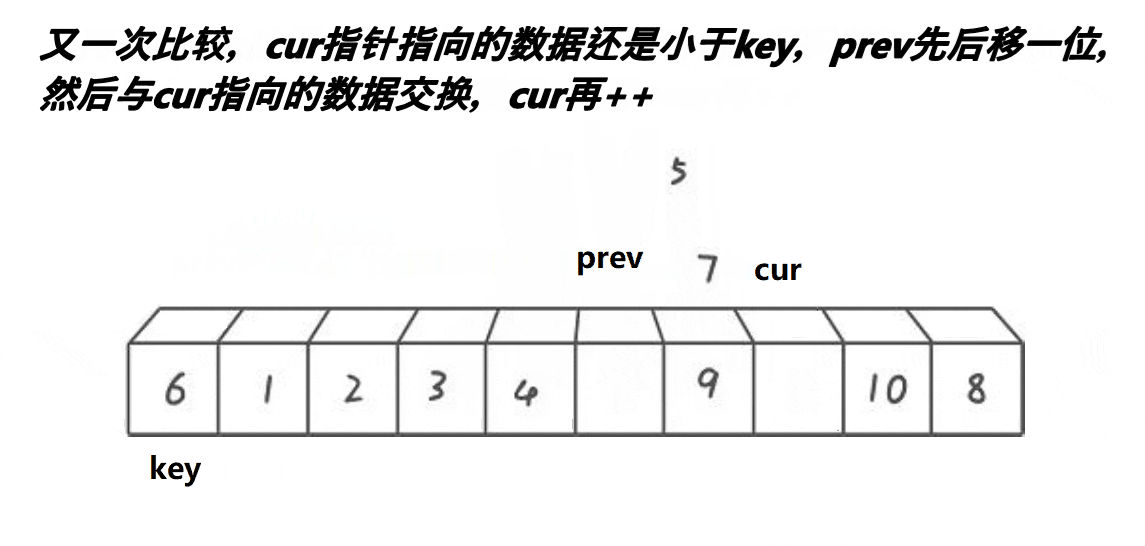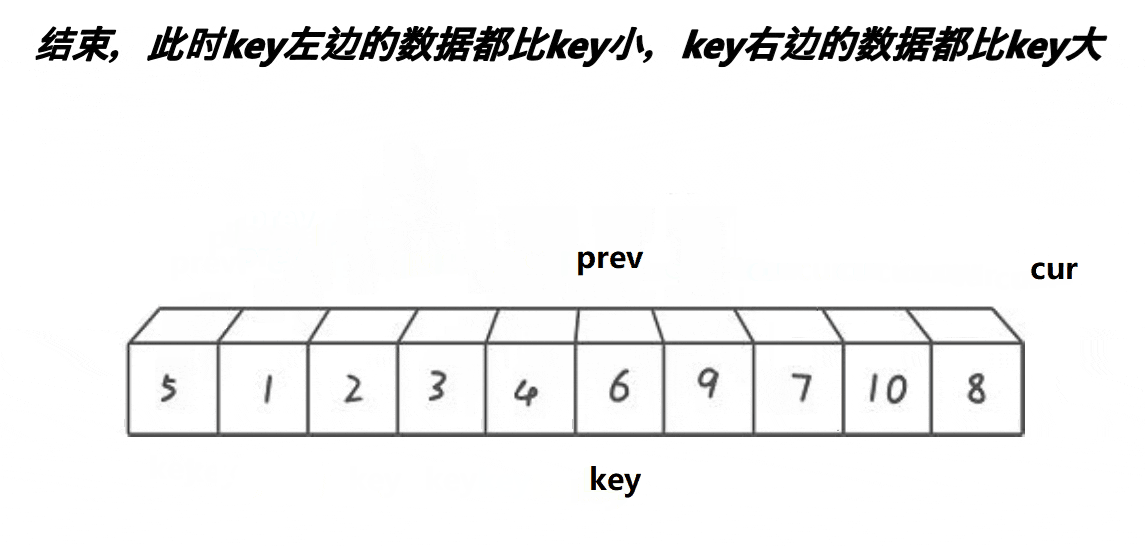
2,定义两个下标,也就是所谓的指针,初始的时候,一个指向最左边第一个元素(prev),一个指向第二个元素(cur),最后定义一个对比keyi3,此时先判断我们的cur是不是小于keyi。cur小于keyi的话:prev++,交换,之后cur++4,但是我们如果和自己交换此时没有什么意义,所以这里我们需要做一个处理
5,继续往前走,如果遇见的是:比keyi下标大的元素此时,cur++,直到遇见的是比keyi下标小的元素,循环执行.prev++,交换,之后cur++6,最后cur走到最后一个元素,我们交换keyi的下标元素和prev的下标元素
多趟实现:
1,递归进行分割:【left,keyi-1】keyi【keyi+1,right】
2,停止条件就是当left>=right
原因:【left, keyi-1】keyi【keyi+1, right】
快排单趟实现
这里只是图解单趟实现逻辑,因为多趟实现的逻辑和霍尔的一样,也是递归,所以不进行多次书写
代码实现
这里的代码实现的核心逻辑不一样,大的框架是一样的,也就是三数取中,以及减少递归从而使用插入排序这样的逻辑是一样的,下面我们来看看这个新的组装怪
//快排(前后指针方法)(递归实现) void QuickSort02(int* a, int left, int right) { //递归停止条件 if (left >= right) return; //创建两个变量,作为前后指针使用 int prev = left; int cur = prev + 1; int keyi = left; //当快指针到尾的时候,跳出循环->交换 while (cur <= right) { //前后指针中间是比a[keyi]大的数值,所以遇见大的++,小的停止 if (a[keyi] > a[cur]) { //停止之后,慢指针++,并且进行交换,因为中间才是大的数值,cur遇见大数值++。遇见小数值才停下来 prev++; Swap(&a[prev], &a[cur]); //同理快指针也进行++,往后移动 cur++; } else { cur++; } } Swap(&a[prev], &a[keyi]); keyi = prev; //多趟递归实现 //[left,keyi-1] keyi [keyi+1,right] 这里传递的是区间 // 1 0 1 2 1 当只剩一个数值的时候,也就是这个区间的时候,递归停止 QuickSort02(a, left, keyi - 1); QuickSort02(a, keyi + 1, right); }总结:
算法基础:快速排序是一种分而治之的排序算法,它通过递归地将数组分为较小的子数组,然后对这些子数组进行排序。
分区策略:使用前后指针(
prev和cur)进行分区,而不是传统的左右指针。这种方法在某些情况下可以减少元素交换的次数。基准值选择:基准值(
keyi)是数组的第一个元素,即left索引对应的元素。指针移动规则:
prev作为慢指针,用于跟踪比基准值小的元素的边界。cur作为快指针,从left + 1开始遍历数组。元素交换:当快指针指向的元素大于基准值时,不进行交换,快指针继续移动;当快指针指向的元素小于或等于基准值时,与慢指针所指元素交换,然后慢指针和快指针都向前移动。
递归排序:在基准值确定之后,递归地对基准值左边和右边的子数组进行排序。
时间复杂度:平均情况下,快速排序的时间复杂度为O(n log n)。最坏情况下,如果每次分区都极不平衡,时间复杂度会退化到O(n^2)。
空间复杂度:由于递归性质,快速排序的空间复杂度为O(log n)。
算法优化:通过前后指针方法,可以在某些情况下提高快速排序的性能,特别是当基准值接近数组中间值时。
适用场景:快速排序适用于大多数需要排序的场景,特别是在大数据集上,它通常能够提供非常高效的排序性能。
优化
这里我们可以看到,cur无论是if还是else里面都需要++,所以我们直接放到外面
其次我们为了效率,不和自己交换,我们不和自己交换,进行一个判断条件
快慢指针代码优化(完整)
//交换函数 void Swap(int* p1, int* p2) { int tmp = *p1; *p1 = *p2; *p2 = tmp; } //快排(前后指针方法)(递归实现) void QuickSort02(int* a, int left, int right) { //递归停止条件 if (left >= right) return; if (right - left + 1 >= 10) { InsertionSort(a + left, right - left + 1); } else { //三数取中 int mid = GetMid(a, left, right); Swap(&a[mid], &a[left]); //单趟实现 //创建两个变量,作为前后指针使用 int prev = left; int cur = prev + 1; int keyi = left; //当快指针到尾的时候,跳出循环->交换 while (cur <= right) { //前后指针中间是比a[keyi]大的数值,所以遇见大的++,小的停止 if (a[keyi] > a[cur] && prev++ != cur) { //停止之后,慢指针++,并且进行交换,因为中间才是大的数值,cur遇见大数值++。遇见小数值才停下来 Swap(&a[prev], &a[cur]); } cur++; } Swap(&a[prev], &a[keyi]); keyi = prev; //多趟递归实现 //[left,keyi-1] keyi [keyi+1,right] 这里传递的是区间 // 1 0 1 2 1 当只剩一个数值的时候,也就是这个区间的时候,递归停止 QuickSort02(a, left, keyi - 1); QuickSort02(a, keyi + 1, right); } }总结:
基本递归结构:算法使用递归调用来处理子数组,这是快速排序算法的核心结构。
小数组优化:当子数组的大小小于或等于10时,算法使用插入排序而不是快速排序,因为插入排序在小规模数据上更高效。
三数取中法:为了更均匀地分割数组,算法使用三数取中法选择基准值,这有助于减少最坏情况发生的概率。
前后指针方法:算法使用两个指针(
prev和cur),其中prev作为慢指针,cur作为快指针,通过这种方式进行一次遍历完成分区。分区操作:快指针从
left + 1开始遍历,如果当前元素小于基准值,则与慢指针所指的元素交换,然后慢指针向前移动。递归排序子数组:基准值确定后,算法递归地对基准值左边和右边的子数组进行排序。
时间复杂度:平均情况下,算法的时间复杂度为O(n log n),最坏情况下为O(n^2)。但由于采用了小数组优化和三数取中法,最坏情况的发生概率降低。
空间复杂度:算法的空间复杂度为O(log n),这主要由于递归调用导致的栈空间使用。
适用场景:这种改进的快速排序算法适用于大多数需要排序的场景,尤其是在大数据集上,它能够提供非常高效的排序性能,同时在小数据集上也表现出较好的效率。
算法稳定性:由于使用了插入排序对小规模子数组进行排序,算法在处理小规模数据时具有稳定性。
注意:在实际测试·里面,前后指针比霍尔排序慢一点
通过这种混合排序策略,算法在保持快速排序优点的同时,也提高了在特定情况下的排序效率,使其成为一种更加健壮的排序方法。
注意事项
这里调用的插入排序是升序,写的快排也是升序,如果你需要测试降序,那么你需要把插入排序一起改成降序,不然会导致排序冲突