1、动态规划(dynamic programming)与分治方法相似,都是通过组合子问题的解 来求解原问题
分治方法 将问题划分为互不相交的子问题,递归地求解子问题,再将它们的解组合起来。求出原问题的解
与之相反,动态规划则用于 子问题重叠的情况,即不同的子问题具有公共的子子问题(子问题的求解是递归进行的,将其划分为更小的子子问题)
分治算法会做许多次冗繁的工作,它会反复地求解那些公共子子问题。而动态规划算法对每个子子问题只求解一次,将其解保存在一个表格中,从而无需每次求解一个子子问题时都重新计算,避免了这种不必要的计算工作
2、动态规划方法通常用来 求解优化问题。这类问题 可以有很多可行解,希望寻找具有最优值(最小值 或 最大值)的解。称这样的解为 问题的一个最优解,而不是最优解,因为可能有多个解都达到最优值
4、按如下4个步骤来设计一个动态规划算法:
- 刻画一个最优解的结构特征
- 递归地定义最优解的值
- 计算最优解的值,通常采用自底向上的方法
- 利用计算出的信息构造一个最优解
仅仅需要 一个最优解的值,而非解本身,可以忽略最后一步。如果确实需要步骤4,有时就需要 在执行步骤3时 维护一些额外信息,以便用来构造一个最优解
1、钢条切割

钢条切割问题:给定一段长度为n英寸的钢条 和 一个价格表P_i(i = 1, 2, …, n),求切割钢条方案,使得销售收益 r_n 最大
最优解可能就是完全不切割钢条
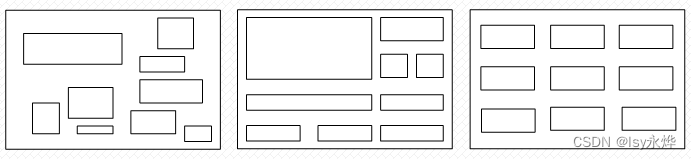
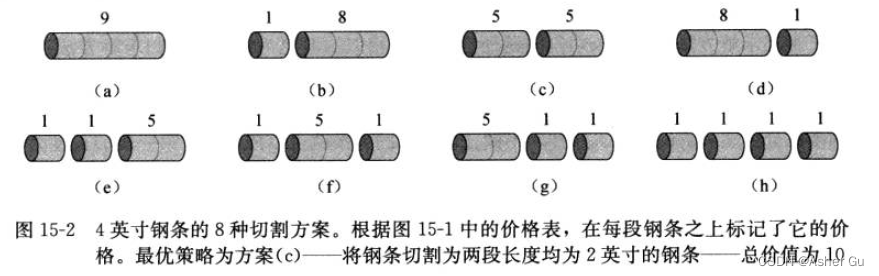
1、给出了4英寸钢条 所有可能的切割方案,包括根本不切割的方案
更一般地,对于r_n (n >= 1),可以用更短的钢条的最优切割收益 来描述它:

第一个参数 p_n 对应不切割,直接出售 长度为 n 英寸的钢条的方案。其他 n - 1 个参数对应另外 n - 1 种方案;首先 将钢条切割为长度为 i 和 n - i 的两段,接着求解这两段的最优切割收益 r_i 和 r_n-i
求解规模更小的子问题,通过组合 两个相关子问题的最优解,并在所有可能的两段切割方案中 选取组合收益最大者,构成原问题的最优解。钢条切割问题 归结为最优子结构性质:问题的最优解 由相关子问题的最优解组合而成,而这些子问题可以独立求解
2、钢条切割问题 还有一种相似 但更为简单的递归求解方法:
将钢条 从左边切下长度为 i 的一段,只对右边剩下的长度为 n - i 的一段继续进行切割 (递归求解),对左边的一段 则不再进行切割。即问题分解的方式为:将长度为 i 的钢条 分解为左边开始一段,以及剩余部分继续分解的结果
可以得到 上面公式 的简化版本

原问题的最优解 只包含一个相关子问题 (右端剩余部分) 的解,而不是两个
3、自顶向下递归实现:
CUT-ROD(p, n)
1 if n == 0
2 return 0
3 q = -∞
4 for i = 1 to n
5 q = max(q, p[i] + CUT-ROD(p, n-i))
6 return q
过程CUT-ROD 返回长度为n的钢条的最大收益。一旦输入规模稍微变大,程序运行时间会变得相当长。每当n增大1,程序运行时间差不多就会增加1倍
为什么 CUT-ROD 的效率这么差?原因在于,CUT-ROD反复地用相同的参数进行递归调用,即 它反复求解相同的子问题,n 每增大1,就会把之前求过的再求一遍

令 T(n) 表示当第二个参数值为 n 时 CUT-ROD 的调用次数,T(0) = 1(每次调用 纵向n减1就结束了 T(n - 1),横向 n - 2 递减至0,看上面例子)
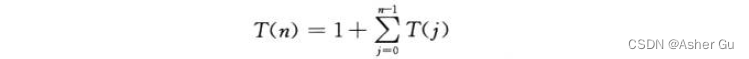
第一项 “1” 表示函数的第一次调用 (递归调用树的根结点),T(j) 为调用 CUT-ROD(p, n-i) 所产生的所有调用 (包括递归调用) 的次数,此处 j = n - i

即 CUT-ROD 的运行时间为 n 的指数函数(可以使用 数学归纳法 证明)
CUT-ROD 考虑了所有 2n-1 种可能的切割方案。递归调用树中 共有 2n-1 个结点,每个叶结点 对应一种可能的钢条切割方案
4、使用动态规划方法 来解决最优钢条切割问题:将 CUT-ROD 转换为一个更高效的动态规划算法
朴素递归算法 之所以效率很低,是因为 它反复求解相同的子问题。动态规划方法在仔细安排求解顺序,对每个子问题 只求解一次,并将结果保存。如果随后需要此问题的解,只需要 查找保存的结果,而不需要 重新计算
动态规划方法 是付出额外的内存空间 来节省计算时间,是典型的 时空均衡 例子,即用空间换取时间。而时间上的节省可能是非常巨大的:可能将一个指数时间的解 转化为 一个多项式时间的解。如果子问题的数量是 输入规模的 多项式函数,可以 在多项式时间内求解出每个子问题,那么动态规划方法的总运行时间 就是多项式阶的
5、动态规划有两种等价的实现方法
1)带备忘的自顶向下法。此方法仍按 自然的递归形式 编写过程,但过程会保存 每个子问题的解 (通常保存在一个数组或散列表中)。当需要一个子问题的解时,过程 首先检查是否已经保存过此解。如果是,则直接返回保存的值,从而节省了计算时间;否则,按通常方式计算这个子问题。这个递归过程是带备忘的,因为它“记住”了已经计算出的结果
自顶向下CUTROD过程的伪代码, 加人了备忘机制
MEMOIZED-CUT-ROD(p, n)
1 let r[0..n] be a new array // 多了个名字为r的记录数组
2 for i = 0 to n
3 r[i] = -∞
4 return MEMOIZED-CUT-ROD-AUX(p, n, r)
MEMOIZED-CUT-ROD-AUX(p, n, r)
1 if r[n] ≥ 0
2 return r[n]
3 if n == 0
4 q = 0
5 else q = -∞
6 for i = 1 to n
7 q = max(q, p[i] + MEMOIZED-CUT-ROD-AUX(p, n-i, r)) // 有个反复递归求解的过程
8 r[n] = q
9 return q
2)自底向上法。这种方法 一般要恰当定义子问题“规模”概念,便得 任何子问题的求解 都只依赖于“更小”的子问题的解。将子问题按规模排序,按从小到大的顺序 进行求解。当求解某个子问题时,它所依赖的 所有更小子问题也必然已求解完成,结果已经保存
也就是说 每个子问题只需求解一次, 当我们求解它(也是第一次遇到它)时,它的所有前提子问题 都已求解完成
两种方法得到的算法具有相同的渐近运行时间, 仅有的差异是 在某些特殊情况下,自顶向下方法 并未其正递归地考察所有可能的子问题。由于没有频繁的递归函数调用的开销,自底向上的时间复杂性函数 通常具有更小的系数
伪代码:
BOTTOM-UP-CUT-ROD(p, n)
1 let r[0..n] be a new array
2 r[0] = 0
3 for j = 1 to n
4 q = -∞
5 for i = 1 to j // 从小到大的循环寻找 而不是递归了
6 q = max(q, p[i] + r[j-i])
7 r[j] = q
8 return r[n]
采用子问题的自然顺序:若i < j,则规模为i的子问题 比规模为j的子问题“更小”。因此,过程依次求解规模为j = 0, 1, …, n的子问题
自底向上算法和自顶向下算法 具有相同的渐进运行时间,BOTTOM-UP-CUT-ROD的主体是 嵌套的双重循环,内层for循环(第5至6行)的迭代次数 构成一个等差数列,运行时间为 Θ(n2)
自顶向下的 MEMOIZED-CUT-ROD 的运行时间也是 Θ(n2),MEMOIZED-CUT-ROD 对 每个子问题只求解一次,而它求解了 规模为 0, 1, …, n 的子问题;为求解 规模为 i 的子问题,第5~6行的循环 会迭代i次,因此,MEMOIZED-CUT-ROD 进行的所有递归调用 执行此for循环的迭代次数 也是一个等差数列,其和也是 Θ(n2)
6、子问题图
当思考一个动态规划问题时,应该弄清所涉及的子问题 及 子问题之间的依赖关系
它是一个有向图,每个顶点 唯一地对应一个子问题
若求子问题x的最优解时 需要直接用到子问题y的最优解,那么 在子问题图中 就会有一条从子问题x的顶点 到子问题y的顶点的有向边
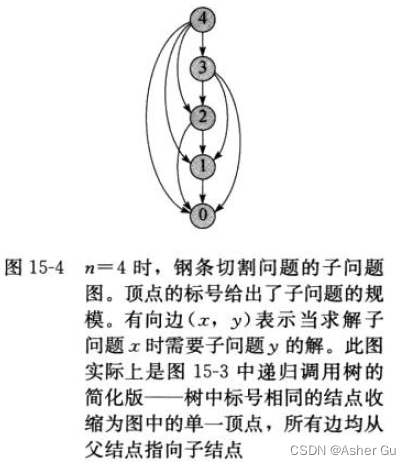
子问题图 G = (V, E) 的规模 可以帮助我们 确定动态规划算法的运行时间。由于每个子问题只求解一次,因此算法运行时间 等于每个子问题求解时间之和。一个子问题的求解时间 与子问题图中对应顶点的度(出射边的数目)成正比,而子问题的数量 等于子问题图的顶点数。动态规划法的运行时间 与顶点和边的数量呈线性关系
7、重构解
前文给出的 钢条切割问题的动态规划算法 返回的最优解的收益值,但并未返回 解本身(一个长度列表,给出切割后 各段钢条的长度)。扩展动态规划算法,使之 对每个子问题不仅保存最优收益值,还保存对应的切割方案
BOTTOM-UP-CUT-ROD的扩展版本,它对长度为j的钢条 不仅计算最大收益值r_j,还保存最优解对应的 第一段钢条的切割长度s_j,然后就可以在 数组中剩下长度的下标中找切的第二刀,以此类推
EXTENDED-BOTTOM-UP-CUT-ROD(p, n)
1 let r[0..n] and s[0..n] be new arrays
2 r[0] = 0
3 for j = 1 to n
4 q = -∞
5 for i = 1 to j
6 if q < p[i] + r[j-i]
7 q = p[i] + r[j-i]
8 s[j] = i
9 r[j] = q
10 return r and s
输出长度为n的钢条的完整的最优切割方案
PRINT-CUT-ROD-SOLUTION(p, n)
1 {r, s} = EXTENDED-BOTTOM-UP-CUT-ROD(p, n)
2 while n > 0
3 print s[n]
4 n = n - s[n] // 从左向右切,剩下的长度
输出直接就是从前往后 切的点 距离最左点的距离
EXTENDED-BOTTOM-UP-CUT-ROD(p, 10) 会返回下面的数组:

对比调用PRINT-CUT-ROD-SOLUTION(p, 10)只会输出10,但对n=7,会输出最优方案r7切割出的两段钢条的长度1和6
8、对钢条切割问题 进行一点修改,除了切割下的钢条段 具有不同价格 p_i 外,每次切割 还要支付固定的成本c。这样,切割方案的收益 等于钢条段的价格之和 减去切割的成本。设计一个动态规划算法解决修改后的钢条切割问题
需要考虑 第5-6行中 循环的每一次迭代的成本c,但最后一次迭代除外,当i=j(无切割)
所以 使循环运行到j−1而不是j,确保从第6行的候选收入中减去c,然后在第7行中选择 当前最佳收入q和p[j](无削减,所以需要在这比一下,之前的比大小 需要减 所以把p[j]排除了)中的较大者
MODIFIED-CUT-ROD(p, n, c)
let r[0..n] be a new array
r[0] = 0
for j = 1 to n
q = p[j]
for i = 1 to j - 1
q = max(q, p[i] + r[j - i] - c)
r[j] = q
return r[n]
使之不仅返回最优收益值,还返回切割方案
MEMOIZED-CUT-ROD(p, n)
let r[0..n] and s[0..n] be new arrays
for i = 0 to n
r[i] = -∞
(val, s) = MEMOIZED-CUT-ROD-AUX(p, n, r, s)
print "The optimal value is" val "and the cuts are at"
j = n
while j > 0
print s[j]
j = j - s[j]
// 自顶向下的方式
MEMOIZED-CUT-ROD-AUX(p, n, r, s) // n为子问题中钢条的长度
if r[n] ≥ 0 // 递归出去的条件
return (r, s)
if n == 0
q = 0
else q = -∞
for i = 1 to n
(val, s) = MEMOIZED-CUT-ROD-AUX(p, n - i, r, s)
if q < p[i] + val
q = p[i] + val
s[n] = i
r[n] = q
return (r, s)
对比自底向上
EXTENDED-BOTTOM-UP-CUT-ROD(p, n)
1 let r[0..n] and s[0..n] be new arrays
2 r[0] = 0
3 for j = 1 to n
4 q = -∞
5 for i = 1 to j
6 if q < p[i] + r[j-i]
7 q = p[i] + r[j-i]
8 s[j] = i
9 r[j] = q
10 return r and s
2、矩阵链乘法
1、求解矩阵链相乘问题的动态规划算法。给定一个n个矩阵的序列(矩阵链)<A1, A2, …, An>,希望计算它们的乘积

由于矩阵乘法满足结合律,因此 任何加括号的方法 都会得到 相同的计算结果. 称有如下性质的矩阵乘积链为 完全括号化的
它是单一矩阵,或者是 两个完全括号化的矩阵乘积链的积,且已外加括号
如果矩阵链为(A_1, A_2, A_3, A_4〉,则共有5种完全括号化的 矩阵乘积链(以 两个相邻矩阵相乘 为线索找)

MATRIX-MULTIPLY(A, B)
1 if A.columns ≠ B.rows
2 error "incompatible dimensions"
3 else let C be a new A.rows × B.columns matrix
4 for i = 1 to A.rows
5 for j = 1 to B.columns
6 c[i, j] = 0
7 for k = 1 to A.columns
8 c[i, j] = c[i, j] + a[i, k] * b[k, j] // 行列两两相乘求和
9 return C
两个矩阵A和B只有相容,即A的列数等于B的行数时,才能相乘
以矩阵链 <A1, A2, A3, A4> 相乘为例,来说明 不同的加括号方式 会导致不同的计算代价。假设这3个矩阵的规模分别为10×100,100×5 和 5 ×50。如果按 ((A1A2)A3) 的顺序计算,为计算 A1A2 (规模10×5),需要做 10·100·5 = 5 000次 (结果矩阵的一个元素 对应 对100对行列乘积 求和) 标量乘法,再与A3相乘又需要做 10·5·50 = 2 500 次标量乘法,共需7 500次标量乘法如果按 ((A1(A2A3))A4) 的顺序,计算 A2A3(规模100×50),需要做 100·5·50 = 250 000次 标量乘法,A1再与之相乘 又需 10·100·50 = 50 000次 标量乘法,共需 300 000次 标量乘法。第一种顺序计算矩阵链乘积 比 第二种顺序 快10倍
矩阵链乘法问题 描述如下:给定n个矩阵的链 <A1, A2, …, An>,矩阵 A_i 的规模为 p_i-1 × p_i (1 <= i <= n),求完全括号化方案,使得计算乘积 A1A2…An 的标量乘法次数最少
求解矩阵链乘法问题 并不是要真正进行矩阵相乘运算,目标 只是确定代价最低的计算顺序。确定 最优计算顺序所花费的时间 通常 比随后真正进行矩阵相乘 所节省的时间(例如仅进行7 500次标量乘法而不是75 000次 )要少
2、计算括号化方案的数量
举所有可能的括号化方案 不会产生一个高效的算法。对一个 n 个矩阵的链,令 P(n) 表示可供选择的括号化方案的数量

递归公式 的结果为 Ω(2n)。因此,括号化方案的数量 与n呈指数关系
3、应用动态规划方法
步骤1:最优括号化方案的结构特征
给出本问题的最优子结构。假设 AiAi+1…Aj 的最优括号化方案的分割点 在 Ak 和 Ak+1 之间。那么,继续对“前缀“子链 AiAi+1···Ak 进行括号化时,应该 直接采用独立求解它时 所得的最优方案。如果不采用独立求解 AiAi+1…Ak 所得的最优方案来对它进行括号化,那么 可以将此最优解 代入AiAi+1···Aj 的最优解中,代替 原来对子链 AiAi+1 … Ak 进行括号化的方案(比AiAi+1···Ak 最优解的代价更高)。显然,这样得到的解 比 AiAi+1…Ak 原来的“最优解”代价更低:产生矛盾
对子链Ak+1Ak+2···Aj,有相似的结论:在原问题AiAi+1…Aj 的最优括号化方案中. 对子链Ak+1Ak+2 …Aj,进行括号化的方法,就是它自身的 最优括号化方案
一个非平凡的矩阵链乘法问题实例的任何解 都需要划分链,而任何最优解 都是由子问题实例的最优解构成的。必须保证 在确定分割点时,已经考察了所有可能的划分点,这样就可以保证 不会遗漏最优解
步骤2:一个递归求解方案
用子问题的最优解 来递归地定义 原问题最优解的代价
将对所有 1 ≤ i ≤ j ≤ n 确定 AiAi+1…Aj 的最小代价 括号化方案作为子问题。令 m[i, j] 表示计算矩阵 Ai…Aj 所需标量乘法次数的最小值,那么,原问题的最优解:计算 A1…n 所需的最低代价就是 m[1, n]
对于 i = j 的平凡问题,矩阵链 只包含唯一的矩阵 Ai…Aj,因此 不需要任何标量乘法运算。因此,对所有 i = 1, 2, …, n,m[i, j] = 0
假设 Ai, …, Aj 的最优括号化方案的分割点 在矩阵 Ak 和 Ak+1 之间,其中 i ≤ k < j。那么,m[i, j] 就等于 计算 Ai 和 Ai+1…j 的代价加上两者相乘的代价的最小值。由于矩阵 Ai 的大小为 p_(i-1) × p_i
如前面所述,Ai…k 与 A_(k+1)…Aj 相乘的代价为 p_(i-1) p_k p_j 次标量乘法运算
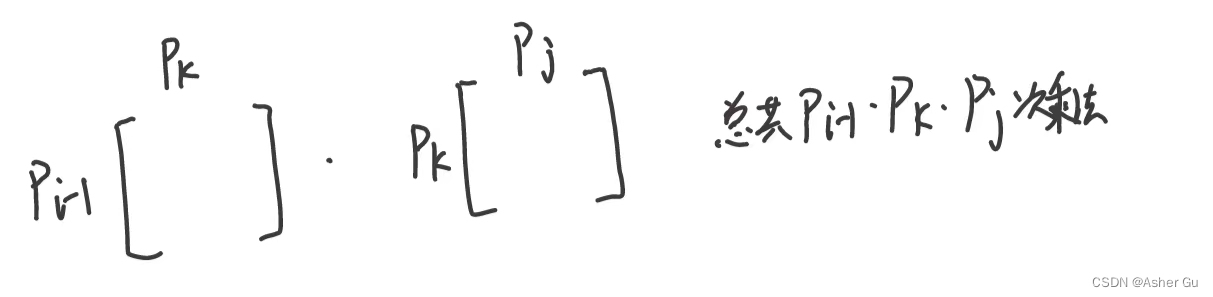

k只有 j - i 种可能的取值,即 k = i, i+1, …, j-1。由于最优分割点 必在其中,我们只需检查所有可能情况,找到最优者即可

m[i, j] 的值给出了 子问题最优解的代价,但它并未提供足够的信息 来构造最优解。为此,用 s[i, j] 来保存 Ai…Aj 最优括号化方案的分割点位置k,即 使得 m[i, j] = m[i, k] + m[k+1, j] + p_(i-1)p_kp_j 成立的k值
步骤3:计算最优代价
每对满足 1<=i<=j<=n 的i和j对应一个唯一的子问题。共有 个。递归算法 会在递归调用树的不同分支中 多次遇到同一个子问题。这种子问题重叠的性质是 应用动态规划的另一个标识(第一个标识是最优子结构)
个。递归算法 会在递归调用树的不同分支中 多次遇到同一个子问题。这种子问题重叠的性质是 应用动态规划的另一个标识(第一个标识是最优子结构)
采用自底向上表格法代替 基于公式(15.7)的递归算法 来计算最优代价.此过程假定矩阵 Ai 的规模为 p_i-1*p_i 过程用一个辅助表m[1…n, 1…n] 来保存代价 m[i, j],用另一个辅助表 s[1…n-1, 2…n] 记录最优值 m[i, j] 对应的分割点k
MATRIX-CHAIN-ORDER(p)
1 n = p.length-1 // 因为需要乘p.length - 1次
2 let m[1..n, 1..n] and s[1..n-1, 2..n] be new tables // 先后的判断 开始长度就是2,所以开始是s[1, 2],结束是s[n-1, n]
3 for i = 1 to n
4 m[i, i] = 0
5 for l = 2 to n // l是乘法链的长度,明显只有一个乘法不需要判断先后
6 for i = 1 to n-l+1
7 j = i + l - 1 // 确保i~j长度是l
8 m[i, j] = ∞
9 for k = i to j-1
10 q = m[i, k] + m[k+1, j] + p[i-1] * p[k] * p[j]
11 if q < m[i, j]
12 m[i, j] = q
13 s[i, j] = k
14 return m and s
图15-5展示了 对一个长度为6的矩阵链(6次乘法)执行此算法的过程。由于 定义 m[i, j] 仅在 i ≤ j 时有意义,因此表m 只使用上对角线之上的部分。图中的表是经过旋转的,主对角线已经旋转到了水平方向
MATRIX-CHAIN-ORDER 按自下而上、自左而右的顺序 计算所有行,当计算表项 m[i, j] 时,会用到乘积 p_i-1 p_k p_j(k = i, i+1, …, j-1),以及 m[i, j] 西南方向(相同i)和东南方向(相同j)上的所有表项

算法的运行时间为 O(n3)。循环嵌套的深度为三层,每层的循环变量 (l, i, k) 最多取n-1个值。MATRIX-CHAIN-ORDER 比起穷举所有可能的括号化方案 来寻找 最优解的指数阶算法更高效
步骤4:构造最优解
表 s[1…n-1, 2…n] 记录了构造最优解所需的信息。每个表项 s[i, j] 记录了一个k值,指出 AiAi+1…Aj 的最优括号化方案的分割点 应该在 Ai 和 A_(i+1) 之间。因此,Ai…n 的最优括号化方案的分割点 应该在 Ak 和 Ak+1 之间
知道 A1…n 的最优计算方案中 最后一次矩阵乘法运算 应该是 A_1…s[1, n] 和 A_s[1, n]+1…n
s[1, s[1, n]] 指出了计算 A_1…s[1, n] 时 应进行的最后一次矩阵乘法运算;s[s[1, n]+1, n] 指出了计算 A_s[1, n]+1…n 时应进行的最后一次矩阵乘法运算
下面 给出的递归过程 可以输出 <Ai,Ai+1, …, Aj> 的最优括号化方案,其输入为 MATRIX-CHAIN-ORDER 得到的表s及下标i和j。调用 PRINT-OPTIMAL-PARENS(s, 1, n) 即可输出 <A1, A2, …, An> 的最优括号化方案
PRINT-OPTIMAL-PARENS(s, i, j)
1 if i == j
2 print "A"i
3 else print "("
4 PRINT-OPTIMAL-PARENS(s, i, s[i, j])
5 PRINT-OPTIMAL-PARENS(s, s[i, j]+1, j)
6 print ")"
调用 PRINT-OPTIMAL-PARENS(s, 1, 6) 输出括号化方案
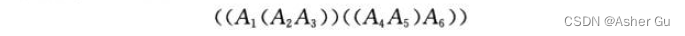
4、证明 对 n个元素的表达式进行完全括号化 ,恰好需要n-1对括号
数学归纳法:通过对矩阵的数量进行归纳来进行证明。
假设一个包含n个元素的表达式的完全括号化 正好有n-1对括号
单个矩阵没有括号对
给定一个包含(n+1)个元素的表达式的完全括号化,必定存在某个k,使得我们首先以某种方式将B=A1⋯Ak相乘,然后以某种方式将C=Ak+1⋯An+1相乘,再将B和C相乘。根据我们的归纳假设,对于B的完全括号化有k-1对括号,对于C的完全括号化有n+1-k-1对括号。得到 (k-1)+(n+1-k-1)+1 = (n+1)-1 对括号
3、动态规划原理
适合应用动态规划方法求解的最优化问题应该具备的两个要素:最优子结构 和 子问题重叠
3.1 最优子结构
1、用动态规划方法求解最优化问题的第一步 就是刻画最优解的结构。如果一个问题的最优解 包含其子问题的最优解,就称 此问题具有最优子结构性质。因此,某个问题 是否适合应用动态规划算法,它是否具有最优子结构性质 是一个好线索(当然,具有最优子结构性质可能意味着适合应用贪心策略,参见第16章)
2、在发掘最优子结构性质的过程中,实际上 遵循了以下通用模式:
- 证明问题最优解的每个组成部分是 做出一个选择。例如,选择钢条第一个切割位置,选择矩阵链划分的位置等。做出这些选择会产生一个或多个待解的子问题
- 对于一个确定问题,在其可能的第一步选择中,假定已经知道 哪种选择会得到最优解。并不关心这种选择具体是如何得到的, 只是假定已经知道了这种选择
- 给定 可获得最优解的选择后,确定这次选择会产生哪些子问题,以及如何最好地 刻画子问题空间
- 利用“剪切-粘贴”技术证明:作为构成原问题最优解的组成部分,每个子问题的解就是它本身的最优解。证明这一点是利用反证法:假定子问题的解 不是其自身的最优问题的解就是它本身的最优解。就可以 从原问题的解中 “剪切" 掉这些非最优解,将最优解“粘贴”进去, 从而得到原问题一个更优的解,这与最初的解是原问题最优解的前提假设 矛盾
3、一个刻划子问题空间的好经验是:保持子问题空间 尽可能简单,只在必要时 才扩展它。例如,求解钢条切割问题时,子问题空间中包含的简单问题为:对每个i值,长度为i的钢条的最优切割问题。这个子问题空间很有效,不必尝试更一般性的子问题空间
假定 试图限制矩阵链 A1A2…Aj 乘法问题的子空间,除非 能保证永远 k=j-1,否则 得到两个形如 A1A2…Ak 和 A(k+1)A(k+2)…An 的子问题,而后者的形态 与 A1A2…Aj 是不同的。因此,对于矩阵链乘法问题,必须允许子问题在“两端”都可以变化,即允许问题 A1A(i+1)…Aj 中i和j都可变
4、对于 不同问题领域,最优子结构的不同 体现在两个方面:
- 原问题的最优解中 涉及多少个子问题
- 在确定最优解 使用哪些子问题时, 需要考察多少种选择
在钢条切割问题中, 长度为n的钢条的最优切割方案 仅仅使用一个子问题(长度为 n-i 的钢条的最优切割), 但必须考察 i 的n种不同取值,来确定哪一个会产生最优解
AiAi+1···Aj 的矩阵链乘法问题中,最优解使用两个子问题, 需要考察 j - i 种情况。 对于给定的矩阵链划分位——矩阵Ak,需要求解两个子问题:AiAi+1…Ak 和 Ak+1Ak+2 …Aj 的括号化方案,而且两个子问题 都必须求解最优方案。一旦 确定了子问题的最优解,就可以在 j - i 个候选的 k 中选取最优者
对于钢条切割问题,其有 Θ(n) 个子问题,每个子问题最多需要考察 n 种选择(包括不切的情况),因此运行时间为 O(n2)。矩阵链乘法问题 共有 Θ(n2) 个子问题,每个子问题 最多需要考察 n-1 种选择,因此运行时间为 O(n3)
5、子问题图也可用来做同样的分析:钢条切割问题的子问题图 有m个顶点,每个顶点最多n条边,因此 运行时间为O(n*m)
6、贪心算法 与 动态规划 有很多相似之处。特别是,能够应用贪心算法的问题 也必须具有最优子结构性质
贪心打法和动态规划最大的不同在于,它并不是 首先寻找子问题的最优解,然后 在其中进行选择,而是 首先做出一次“贪心”选择——在当时(局部)看起来 最优的选择——然后 求解选出的子问题,从而 不必费心求解 所有可能 相关的子问题
7、在尝试使用动态规划方法时要小心,要注意问题是否具有最优子结构性质:
无权最短路径:找到 一条从 u 到 v 的边数最少的路径。这条路径 必然是简单路径,因为 如果路径中包含环,将环去掉是会减少边的数量
无权最长路径:找到 一条从 u 到 v 的边数最多的简单路径
证明 无权最短路径问题 具有最优子结构性质。假设 u != v,从 u 到 v 的任意路径p 都必须包含一个中间顶点,将路径 u -p-> v 分解为两段子路径 u -p1-> w -p2-> v
断言:如果 p 是从 u 到 v 的最优(即最短)路径。那么 p1 必须是从u到w的最短路径
可以用“剪切-粘贴“方法来证明: 如果存在另一条从u到w的路径p1’,其边数比 p1 少, 那么可以剪切掉 p1, 将 p1‘ 粘贴上,
构造出一条比 p 边数更少的路径 u -p1-> w -p2-> v,与p最优的假设矛盾。对称地,p2 必须是 从 w 到 v 的最短路径。因此,可以通过考察 所有中间结点 w 来求 u 到 v 的最短路径,对每个中间顶点w, 求 u 到 w 和 w 到 v 的最短路径, 然后 选择两条路径之和最短的顶点w
最长简单路径问题 不仅缺乏最优子结构的性质,由子问题的解 组合出的 甚至都不是 原问题的“合法解”。组合最长简单路径 q -> s -> t -> r 和 r -> q -> s ->t, 得到的是路径 q -> s -> t -> r -> q -> s -> t, 并不是简单路径

最长简单路径问题的子结构与最短路径差别:
虽然 最长路径问题 和 最短路径问题的解 都用到了两个子问题,但两个最长简单路径子问题是相关的, 而两个最短路径子问题是无关的
即同一个原问题的一个子问题的解 不影响另一个子问题的解,求 q 到 t 的最长简单路径 可以分解为两个子问题 求q到r的最长简单路径 和 r到t的最长简单路径. 对于前者, 选择路径 q -> s -> t -> r,其中 用到了顶点 s 和 t。由于 两个子问题的解的组合 必须产生一条简单路径,因此 在求解第二个子问题时 就不能再用这两个顶点了。但如果 在求解第二个子问题时不允许使用顶点,就根本无法进行下去了,因为 t 是原问题解的路径终点,是必须用到的,还不像子问题解 的“接合”顶点 r 那样可以不用。这样, 由于一个子问题的解 使用了顶点 s 和 t, 在另一个子问题的解中 就不能再使用它们,但其中 至少一个顶点在求解第二个子问题时 又必须用到,而获得最优解 则两个都要用到。因此,说两个子问题是相关的
求解一个子问题时 用到了某些资源(在本例中是顶点),导致 这些资源 在求解其他子问题时不可用
8、求解最短路径的子问题间 为什么是无关的:
根本原因在于,最短路径子问题间 是不共享资源的(求解范围没有交集)
假定 某个顶点 x != w 同时出现在路径 p_1 和 p_2,就可以 将 p1 分解为 
根据 最优子结构性质,路径 p 的边数 等于 p_1 和 p_2 边数之和,假定为 e。接下来 我们构造一条 u 到 v 的路径 
由于已经删掉 x 到 w 和 w 到 x 的路径,每条路径 至少包含一条边,因此 p’ 最多包含 e - 2 条边,与 p 为最短路径的假设 矛盾
因此, 可以保证 最短路径问题的子问题间是无关的
9、在矩阵链乘法问题中,子问题为 子链 Ai Ai+1 … Ak 和 Ak+1 Ak+2 … Aj 的乘法问题,子链是 互不相交的,因此任何矩阵都不会同时包含在两条子链中。在钢条切割问题中,由于长度为 n 的问题的最优解 只包含一个子问题的解,子问题无关性 显然是可以保证的
3.2 重叠子问题
1、适合用 动态规划方法求解的最优化问题 应该具备的第二个性质是 子问题空间必须足够“小”,即问题的递归算法 会反复地求解相同的子问题,而不是 一直生成新的子问题
不同子问题的总数是 输入规模的多项式函数为好。如果 递归算法 反复求解相同的子问题,就称最优化问题具有重叠子问题性质
适合用分治方法求解的问题 通常在递归的每一步都生成全新的子问题
2、动态规划算法 通常这样利用重叠子问题性质:对每个子问题求解一次,将解存入一个表中,当再次需要 这个子问题时直接查表,每次查表的代价为 常量时间
3、计算矩阵链乘法 Ai…j = AiAi+1…Aj 所需最少标量乘法运算次数 m[i, j],而计算过程是低效的。这个过程直接基于递归式:

RECURSIVE-MATRIX-CHAIN(p, i, j)
if i == j
return 0
m[i, j] = ∞
for k = i to j-1
q = RECURSIVE-MATRIX-CHAIN (p, i, k) + RECURSIVE-MATRIX-CHAIN (p, k+1, j) + p_i-1 p_k p_j
if q < m[i, j]
m[i, j] = q
return m[i, j]
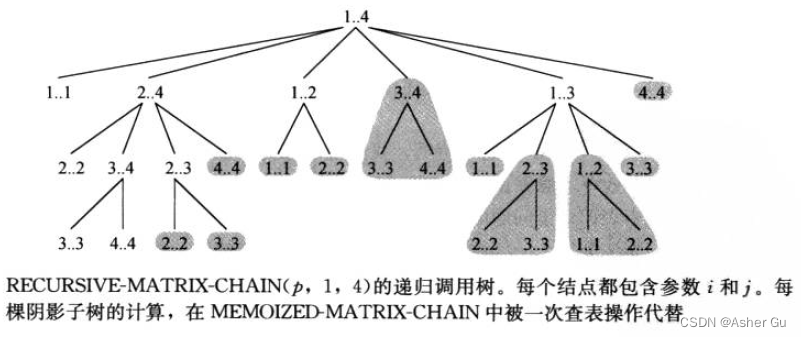
可以证明此过程计算 m[1,n] 的时间至少是 n的指数函数

每一项 T(i) 在公式中 以 T(k) 的形式出现了一次,还以 T(n - k) 的形式出现了一次,而求和项中累加了 n - 1 个 1, 在求和项之前还加了1,因此公式可改写为

利用数学归纳法证明:

调用 RECURSIVE-MATRIX-CHAIN(p, 1, n) 所做的总工作量 至少是n的指数函数
将此 自顶向下的递归算法(无备忘)与 自底向上的动态规划算法 进行比较。后者要有效得多,因为它利用了重叠子问题性质。矩阵链乘法问题只有 Θ(n2)个不同的子问题。动态规划算法对每个子问题只求解一次。而递归算法则相反,对每个子问题.每当在递归树中(递归调用时)遇到它,都要重新计算一次
凡是一个问题的自然递归算法的递归调用树中 反复出现相同的子问题,而不同子问题的总数很少时.动态规划方法都能提高效率
3.3 重构最优解
1、将每个子问题所做的选择 存在一个表中,这样就不必根据代价值来重构这些信息
假定 没有维护 s[i, j]表,只是在表 m[i, j] 中 记录了子问题的最优代价。确定 AiAi+1…Aj 的最优括号化方案 用到了哪些子问题时, 就需要检查所有 j - i 种可能,而 j - i 并不是一个常数。因此,对一个给定问题的最优解,重构它用到了哪些子问题 就需花费 O(j - i) 的时间。而通过在 s[i, j] 中保存 AiAi+1 … Aj 的划分位置,重构每次选择只需 O(1) 时间
2、备忘:
带备忘的递归算法 为每个子问题维护一个表项来保存它的解。每个表项的初值 设为一个特殊值,表示尚未填入子问题的解。当递归调用过程中 第一次遇到子问题时,计算其解,并存入对应表项。随后每次遇到 同一个子问题,只是简单地查表,返回其解
带备忘的 RECURSIVE-MATRIX-CHAIN版本(带备忘的自顶向下)
MEMOIZED-MATRIX-CHAIN(p)
1 n = p.length - 1
2 let m[1..n, 1..n] be a new table
3 for i = 1 to n
4 for j = i to n
5 m[i,j] = ∞
6 return LOOKUP-CHAIN(m, p, 1, n)
LOOKUP-CHAIN(m, p, i, j)
1 if m[i,j]<∞
2 return m[i,j]
3 if i==j
4 m[i,j]=0
5 else for k = i to j-1
6 q = LOOKUP-CHAIN(m, p, i, k)
7 + LOOKUP-CHAIN(m, p, k+1, j) + p[i-1]p[k]p[j]
8 if q < m[i, j]
9 m[i, j] = q
10 return m[i,j]
MEMOIZED-MATRIX-CHAIN 的运行时间为O(n³)。MEMOIZED-MATRIX-CHAIN 的第5行运行了Θ(n²)次。可以将对 LOOKUP-CHAIN 的调用分为两类:
- 调用时 m[i, j] = ∞,因此第3~9行会执行
- 调用时 m[i, j] < ∞,因此 LOOKUP-CHAIN 执行第2行,简单返回值
第一种调用会发生 Θ(n²) 次,每个表项一次。每二种调用 均为第一种调用 所产生的递归调用。而无论何时一个 LOOKUP-CHAIN的调用继续进行递归调用, 都会产生 O(n) 次递归调用
因此,第二种调用共 O(n³) 次,每次花费 O(1) 时间。而第一种调用花费 O(n) 时间再加上它产生的递归调用的时间
因此,算法的总时间为 O(n3)
通常情况下, 如果每个子问题都必须至少求解一次,自底向上动态规划算法 会比自顶向下备忘算法快(都是 O(n3) 时间,相差一个常量系数), 因为自底向上算法 没有递归调用的开销,表的维护开销也更小
而且,对于某些问题,可以利用表的访问模式 来进一步降低时空代价
相反, 如果子问题空间中的某些子问题完全不必求解,备忘方法就会体现出优势了,因为 它只会求解那些绝对必要的子问题
3、如前所述,使用动态规划方法,我们首先求解子问题,然后选择哪些子问题用来构造原问题的最优解。
Capulet教授认为 不必为了求原问题的最优解 而总是求解所有子问题。在求矩阵链乘法问题的最优解时,总是可以在求解子问题之前 选定AiAi+1…Aj 的划分位置 Ak(选定的 k 使得 p_i-1p_kp_j 最大)。请想出一个反例,证明这个贪心方法可能生成次优解

4、最长公共子序列
1、比较两个(或多个)不同生物体的DNA。一个DNA串 由一串称为碱基的分子组成,碱基有腺嘌呤、鸟嘌呤、胞嘧啶和胸腺嘧啶4种类型。将一个DNA串表示为有限集 {A, C, G, T} 上的一个字符串
比较两个DNA串的一个原因是 希望找出它们相似度,作为度量序列相似度的指标
相似定义:如果将一个串转换为另一个串 所需的操作很少,那么可以说两个串是相似的
寻找第三个串S3, 它的所有碱基也都出现在 S1 和 S2 中,且在三个串中 出现的顺序都相同,但在 S1 和 S2 中不要求连续出现。可以找到的 S3 越长,就可以认为 S1 和 S2 相似度越高
2、最长公共子序列问题:一个给定序列的子序列,就是将给定序列中 零个或多个元素去掉之后得到的结果
如果 Z 既是 X 的子序列,也是 Y 的子序列,我们称 Z 是 X 和 Y 的公共子序列
4.1 - 4.4 为4个步骤
4.1 刻画最长公共子序列的特征
1、X 的每个子序列对应下标集合 {1, 2, … , m} 的一个子集,所以 X 有 2m 个子序列(每个位置上有数字和没有数字 两种可能)
LCS 问题具有最优子结构性质
前缀的严谨定义如下:给定一个序列 X = <x_1, x_2, x_3, …, x_m> ,对 i=0, 1, …, m 定义 X 的第 i 前缀为 X_i = <x_1, x_2, x_3, …, x_i>

4.2 一个递归解
1、如果 x_m=y_n,应该求解 Xm - 1 和 Yn - 1 的一个LCS。将 x_m = y_n 追加到这个LCS的末尾
如果 x_m != y_n,必须求解两个子问题:求 X_m-1 和 Y 的一个 LCS
与 X 和 Yn-1 的一个 LCS。两个 LCS较长者 即为 X 和 Y 的一个LCS
LCS 问题的重复子问题性质,很多其他子问题 也都共享子子问题
与矩阵链乘法问题相似,设计 LCS 问题的递归算法 首先要建立最优解的递归式。定义 c[i, j] 表示 X_i 和 Y_j 的 LCS 的长度

在递归公式中,通过限制条件 限定了需要求解哪些子问题。而 在之前讨论的 钢条切割问题 和 矩阵链乘法问题 的动态规划算法中,根据问题的条件,没有排除任何子问题
4.3 计算 LCS 的长度
1、由于 LCS 问题只有 Θ(mn) 个不同的子问题,可以用动态规划方法 自底向上地计算
过程 LCS-LENGTH 接受两个序列 X = <x_1, x_2, …, x_m> 和 Y = <y_1, y_2, …, y_n> 为输入。它将 c[i, j] 的值保存在 线性表 c[0…m, 0…n] 中,并按行主次序 计算表项(即首先计算表的左至右行标的每行,然后计算第二行,依此类推)。过程还维护一个表 b[1…m, 1…n],帮助构建最优解,b[i, j] 指向的表项对应计算 c[i, j] 时所选的子问题优解。过程返回表 c 和表 b,c[m, n] 保存了 X 和 Y 的 LCS 的长度
LCS-LENGTH(X,Y)
1 m = X.length
2 n = Y.length
3 let b[1..m, 1..n] and c[0..m, 0..n] be new tables
4 for i = 1 to m
5 c[i,0] = 0
6 for j = 0 to n
7 c[0,j] = 0 // 有一个是空的,自然长度是0
8 for i = 1 to m
9 for j = 1 to n
10 if x_i = y_j
11 c[i,j] = c[i-1,j-1] + 1
12 b[i,j] = "↖" // 下一个元素在左上角
13 elseif c[i-1,j] >= c[i,j-1]
14 c[i,j] = c[i-1,j]
15 b[i,j] = "↑"
16 else
17 c[i,j] = c[i,j-1]
18 b[i,j] = "←"
19 return c and b
LCS-LENGTH 对输入序列 X = < A, B, C, B, D, A, B> 和 Y =<B, D, C, A, B, A> 的运行过程。过程的运行时间为 Θ(mn),因为每个表项的计算时间为 Θ(1)

设计 LCS-LENGTH 的自顶向下的备忘版本。运行时间为 O(mn)
MEMOIZED-LCS-LENGTH(X, Y, i, j)
if c[i, j] > -1
return c[i, j]
if i == 0 or j == 0
return c[i, j] = 0
if x[i] == y[j]
return c[i, j] = LCS-LENGTH(X, Y, i - 1, j - 1) + 1
return c[i, j] = max(LCS-LENGTH(X, Y, i - 1, j), LCS-LENGTH(X, Y, i, j - 1))
4.4 构造LCS
1、只需简单地从 b[m, n] 开始,开始 按箭头方向追踪下去即可。当在表项 b[i, j] 中遇到一个 “↖” 时,意味着 x_i = y_j 是 LCS 的一个元素。可以按逆序打印依次构造出的 LCS 的所有元素。下面的递归过程 会按正确的顺序打印出 X 和 Y 的一个 LCS。对它的起始调用为 PRINT-LCS(b, X, X.length, Y.length)
PRINT-LCS(b, X, i, j)
1 if i == 0 or j == 0
2 return
3 if b[i,j] == "↖" // 只有碰到左上箭头才需要打印当前所指元素
4 PRINT-LCS(b, X, i-1, j-1)
5 print x_i // 顺序输出
6 elseif b[i,j] == "↑"
7 PRINT-LCS(b, X, i-1, j)
8 else PRINT-LCS(b, X, i, j-1)
过程的运行时间为 O(m+n),因为每次递归调用 i 和 j 至少有一个会减少 1
求 <1, 0, 0, 1, 0, 1, 0, 1> 和 <0, 1, 0, 1, 1, 0, 1, 1, 0> 的一个 LCS
<- / ↑ 在两个一样的情况下任意选一个优先(本人是选的<-优先,书本选择的是 ↑ 优先)

利用完整的表 c 及原始序列 X = < x_1, x_2, …, x_m > 和 Y = < y_1, y_2, …, y_n > 来重构 LCS。要求运行时间为 O(m+n),不能使用表 b
PRINT-LCS(c, X, Y, i, j)
if c[i, j] == 0
return
if X[i] == Y[j] // 只有相等才输出,两个序列同时减少1
PRINT-LCS(c, X, Y, i - 1, j - 1)
print X[i]
else if c[i - 1, j] > c[i, j - 1] // 哪个长就选哪个
PRINT-LCS(c, X, Y, i - 1, j)
else
PRINT-LCS(c, X, Y, i, j - 1)
4.5 算法改进
1、对 LCS 算法,我们完全可以去掉表 b。每个 c[i, j] 项只依赖于表 c 中的其他三项:c[i−1, j−1], c[i, j], c[i, j−1] 和 c[i, j−1],给定 c[i,j] 的值,可以在 O(1) 时间内判断出在 计算 c[i, j] 时使用了这三项中的哪一项
可以用一个类似 PRINT-LCS 的过程在 O(m+n) 时间内完成构造 LCS 的工作,而且不必使用表 b。这种方法节省了 Θ(mn) 的空间,但计算 LCS 所需的辅助空间并未渐近减少
2、LCS-LENGTH 的空间需求是 可以渐近减少的,因为在任何时刻它只需要表 c 中的两行:当前正在计算的一行和前一行
如果 只需计算 LCS 的长度,这一改进是有效的,但如果需要重构 LCS 中的元素,这么小的表空间所保存的信息 不足以在 O(m+n) 时间内完成重构工作
如何使用 min(m, n) 个空间记录 和 O(1) 的额外空间来完成相同的工作
只使用 c 表的上一行来计算当前行,当我们计算第 k 行时,我们释放第 k-2 行,因为不需要它来计算长度。为了使用更少的空间,观察到计算 c[i, j] 时,我们只需要条目 c[i-1, j], c[i-1, j-1], 和 c[i, j-1]。因此,可以逐项释放那些 再也不需要的上一行的条目,从而将空间需求减少到 min(m, n)。从依赖的三个条目中计算下一个条目需要 O(1) 的时间和空间
3、设计一个 O(n log n) 的算法,求一个 n 数的序列的最长单调递增子序列
给定一个数字列表 L,创建 L 的副本 L′,然后对 L′ 进行排序
L和L’就是X和Y
PRINT-LCS(c, X, Y)
n = c[X.length, Y.length]
let s[1..n] be a new array
i = X.length
j = Y.length
while i > 0 and j > 0
if x[i] == y[j]
s[n] = x[i]
n = n - 1
i = i - 1
j = j - 1
else if c[i - 1, j] ≥ c[i, j - 1]
i = i - 1
else j = j - 1
for i = 1 to s.length
print s[i]
MEMO-LCS-LENGTH-AUX(X, Y, c, b)
m = |X|
n = |Y|
if c[m, n] != 0 or m == 0 or n == 0
return
if x[m] == y[n]
b[m, n] = ↖
c[m, n] = MEMO-LCS-LENGTH-AUX(X[1..m - 1], Y[1..n - 1], c, b) + 1
else if MEMO-LCS-LENGTH-AUX(X[1..m - 1], Y, c, b) ≥ MEMO-LCS-LENGTH-AUX(X, Y[1..n - 1], c, b)
b[m, n] = ↑
c[m, n] = MEMO-LCS-LENGTH-AUX(X[1..m - 1], Y, c, b)
else
b[m, n] = ←
c[m, n] = MEMO-LCS-LENGTH-AUX(X, Y[1..n - 1], c, b)
MEMO-LCS-LENGTH(X, Y)
let c[1..|X|, 1..|Y|] and b[1..|X|, 1..|Y|] be new tables
MEMO-LCS-LENGTH-AUX(X, Y, c, b)
return c and b
5、最优二叉搜索树
1、设计一个程序,实现英语文本到法语的翻译。对英语文本中出现的每个单词,需要查找 对应的法语单词。可以创建一棵二叉搜索树,将n个英语单词 作为关键字, 对应的法语单词 作为关联数据
由于 对文本中的每个单词 都要进行搜索,希望花费在搜索上的总时间尽量少,通过使用红黑树或其他平衡搜索树结构,可以假定 每次搜索时间为 O(lgn)。但是, 单词出现的频率是不同的,频繁使用的单词 有可能位于搜索树中远离根的位置上,而 很少使用的单词 可能位于靠近根的位置上,这样的结构会减慢翻译的速度
因为 在二叉树搜索树中 搜索一个关键字需要访问的结点数等于 包含关键字的结点的深度加1(根结点的深度是0,如果目标结点的深度是 d,那么从根结点到目标结点一共需要经过 d 条边)
希望文本中频繁出现的单词 被置于 靠近根的位置,而且 文本中的一些单词 可能没有对应的法语单词,这些单词根本不应该出现在二叉搜索树中
2、在给定单词出现频率的前提下,应该如何组织一棵二叉搜索树,使得 所有搜索操作 访问的结点总数最少
即最优二叉搜索树问题,其形式化定义如下:
给定一个 n个不同关键字的 已排序的序列 K = <k1, k2, …, kn>(因此 k1 < k2 < … <kn),希望用这些关键字构造一棵二叉搜索树。对每个关键字 k_i,都有一个概率 p_i 表示其搜索频率
有些要搜索的值 可能不在 K 中, 因此 还有 n + 1 个 “伪关键字” d0, d1, d2, ··, dn 表示不在K中的值。d0 表示所有小于 k_1 的值,d_i 表示所有大于 k_n 的值,对 i = 1, 2, ···, n-1,伪关键字 d_i 表示 所有在 k_i 和 k_i+1 之间的值。对每个伪关键字 d_i, 也都有一个概率 q_i 表示对应的搜索频率
每个关键字 k_i 是一个内部结点,而每个伪关键字 d_i 是一个叶结点。每次搜索要么成功(找到某个关键字 k_i) 要么失败(找到某个伪关键字 d_i
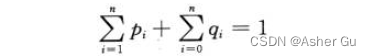

知道 每个关键字和伪关键字的搜索概率,因而 可以确定在一棵给定的二叉搜索树T中 进行一次搜索的期望代价:

希望构造一棵期望搜索代价最小的二叉搜索树,称之为最优二叉搜索树
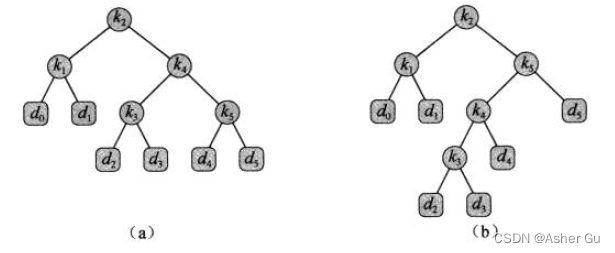
(b)就是给定概率集合的最优二叉搜索树,其期堕代价为2 75。这个例子显示,最优二叉搜索树不一定是高度最矮的,而且概率最高的关键字 也不一定出现在二义搜索树的根结点(因为 结点在树中的相对位置必须满足排序要求,概率最高的结点可能会被放置在一个位置,使得整体搜索时间最小化,而不是单独考虑其在根结点的位置),在此例中,关键字 k5 的搜索概率最高,旦 最优二叉搜索树的根结点为 k_2(在所有 以 k_5 为根的二叉搜索树中,期望搜索代价最小者为2.85)
与 矩阵链乘法问题 相似,穷举并检查所有可能的二叉搜索树 不是一个高效的算法。对任意一棵 n 个结点的二叉树,都可以通过对结点标记关键字 k_1, k_2, …, k_n,构造一棵二叉搜索树,然后 向其中添加 伪关键字作为叶子节点
5.1 - 5.3 为3个步骤
5.1 最优二叉搜索树的结构
1、从观察子树特征开始。考虑一棵二叉搜索树的任意子树。它必须包含连续关键字 k_i, k_i+1, …, k_j,其叶结点 必然是 伪关键字 d_i-1, …, d_j
二叉搜索树问题的最优子结构:一棵最优二叉搜索树 T 有一棵包含关键字 k_i, k_i+1, …, k_j 的子树 T’,那么 T’ 必然是包含关键字 k_i, k_i+1, …, k_j 和伪关键字 d_i-1, …, d_j 的子问题的最优解。
使用 剪切-粘贴法证明这一结论。如果存在子树 T’,其期望搜索代价比 T’ 低,那么将 T’ 从 T 中删除,从而得到一棵期望搜索代价低于 T 的二叉搜索树,与 T 最优的假设矛盾
需要用 最优子结构性质 来证明,可以 用子问题的最优解 构造原问题的最优解。给定关键字 k_i, k_i+1, …, k_j,其中某个关键字k_r (i <= r <= j) 是 最优子树的根结点,那么 k_r 的左子树 包含关键字 k_i, …, k_r-1(和伪关键字 d_i-1, …, d_r-1),而右子树包含关键字 k_r+1, …, k_j(和伪关键字 d_r 和 d_j)
只要 检查所有可能的根结点 k_r (i <= r <= j),并对每种情况分别求解包含 k_i, ···, k_r-1 及包含 k_r+1, …, k_j 的最优二叉搜索树,即可保证找到原问题的最优解
2、空子树:选定 k 为根结点,k_i 的左子树包含关键字 k_i, … , k_i-1。将此序列 解释为不包含任何关键字,但请注意,子树仍然包含伪关键字
包含关键字序列 k_i, …, k_i-1 的子树 不含任何实际关键字,但包含单一伪关键字 d_i-1
5.2 一个递归算法
1、选取子问题域为:求解包含关键字 k_i, …, k_j 的最优二叉搜索树,其中 i >= 1,j <= n 且 j >= i-1。定义 e[i, j] 为包含关键字 k_i, …, k_j 的最优二叉搜索树中 进行一次搜索的期望代价
2、j = i-1 的情况最为简单,由于 子树只包含伪关键字 d_i-1,期望搜索代价为 e[i, i-1] = q_i-1
当 j >= i 时,需要从 k_i, ··, k_j 中选择一个根结点 k_r,然后构造一棵包含关键字 k_i, ···, k_r-1 的最优二叉搜索树 作为其左子树,以及一棵包含关键字 k_r+1, …, k_j 的二叉搜索树作为其右子树。当一棵子树成为一个结点的子树时,期望搜索代价的变化:
由于每个结点的深度都增加了1,根据公式
这棵子树的期望搜索代价的增加值 应为所有概率之和,对于包含关键字 k_i,…,k_j 的子树,所有概率之和为

因此 ,若 k_r 为包含关键字 k_i,…,k_j 的最优二叉搜索树的根结点,有如下公式
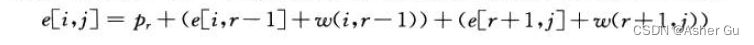
只有 p_r 没有 q_r,w拆分 q 不会有缺项
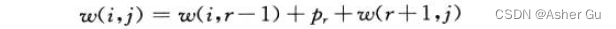
因此 e[i, j] 可重写为

假定 知道哪个结点 k 应该作为根结点。如果选取 期望搜索代价最低者 作为根结点, 可得最终递归公式

e[i, j] 的值给出了 最优二叉搜索树的期待搜索代价,定义 root[i, j] 保存根结点 k_r 的下标 r
5.3 计算最优二叉搜索树的期望搜索代价
1、求解最优二叉搜索树 和 矩阵链乘法 的一些相似之处。它们的子问题都 由连续的下标域组成。直接递归实现,与矩阵链乘法问题的直接递归算法 一样低效
用一个表 e[1…n+1, 0…n] 来保存 e[i, j] 值。第一维下标上界为 n + 1 而不是 n,原因在于 对于只包含伪关键字 d_n 的子树,需要计算并保存 e[n+1, n]。第二维下标下界为0,是因为对于 只包含伪关键字 d_0 的子树,需要计算并保存 e[n + 1, n]。只使用表中满足 j >= i-1 的表项 e[1, 0]。还使用一个表 root,表项 root[i, j] 记录包含关键字 k_i, …, k_j 的子树的根,只使用此表中满足 1 <= i <= j <= n 的表项 root[i, j]
还需要 另一个表来提高计算效率。为了避免 每次计算 e[i, j] 时都重新计算 w(i, j), 将这些值保存在表 w[1…n+1, 0…n] 中,这样每次可节省 Θ(j - i) 次加法。对基本情况,令 
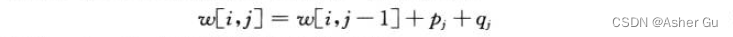
对 Θ(n2) 个 w[i, j],每个的计算时间为 Θ(1)
伪代码接受概率列表 p_1, …, p_n 和 q_0 … ,q_n 及规模n作为输入,返回表 e 和 root
OPTIMAL-BST(p, q, n)
1 let e[1..n+1, 0..n], w[1..n+1, 0..n], and root[1..n, 1..n] be new tables
2 for i = 1 to n+1
3 w[i, i-1] = q_i-1
4 e[i, i-1] = q_i-1
5 for l = 1 to n // 长度
6 for i = 1 to n-l+1 // 起始点
7 j = i + l - 1 // i = n - i + 1 代入就是n
8 e[i, j] = ∞
9 w[i, j] = w[i, j-1] + p_j + q_j // 算完就不更新了
10 for r = i to j // 以不同的结点为根
11 t = e[i, r-1] + e[r+1, j] + w[i, j]
12 if t < e[i, j]
13 e[i, j] = t
14 root[i, j] = r // 记录根
15 return e and root

OPTIMAL-BST 输入上图的关键字分布后 计算出的表 e[i, j] 、w[i, j] 和 root[i, j]
对角线旋转到了水平方向,OPTIMAL-BST 按自底向上的顺序逐行计算,在每行中由左至右计算每个表项

与 MATRIX-CHAIN-ORDER 一样,OPTIMAL-BST 的时间复杂度也是 θ(n3)。由于它包含三重 for 循环,而每层循环的下标最多取 n 个值,因此很容易得出其运行时间为 O(n3)
2、设计伪代码 CONSTRUCT-OPTIMAL-BST(root),输入为表 root,输出是最优二叉搜索树的结构
CONSTRUCT-OPTIMAL-BST(root, i, j, last)
if i == j
return
if last == 0
print root[i, j] + "is the root"
else if j < last
print root[i, j] + "is the left child of" + last
else
print root[i, j] + "is the right child of" + last
CONSTRUCT-OPTIMAL-BST(root, i, root[i, j] - 1, root[i, j])
CONSTRUCT-OPTIMAL-BST(root, root[i, j] + 1, j, root[i, j])
last 是根,且 与i, j一起用来判断是 左右子树
3、