1.引言
查找和排序算法是算法的入门知识,其经典思想可以用于比较常见。
1.1 内部排序和外部排序的区别
内部排序:待排序记录存放在计算机随机存储器中(内存)进行排序的过程。
外部排序:待排序记录的数量很大,以至于内存不能一次容纳全部记录,所以在排序过程中需要对外存进行访问的排序过程
1.2 内部排序算法的分类
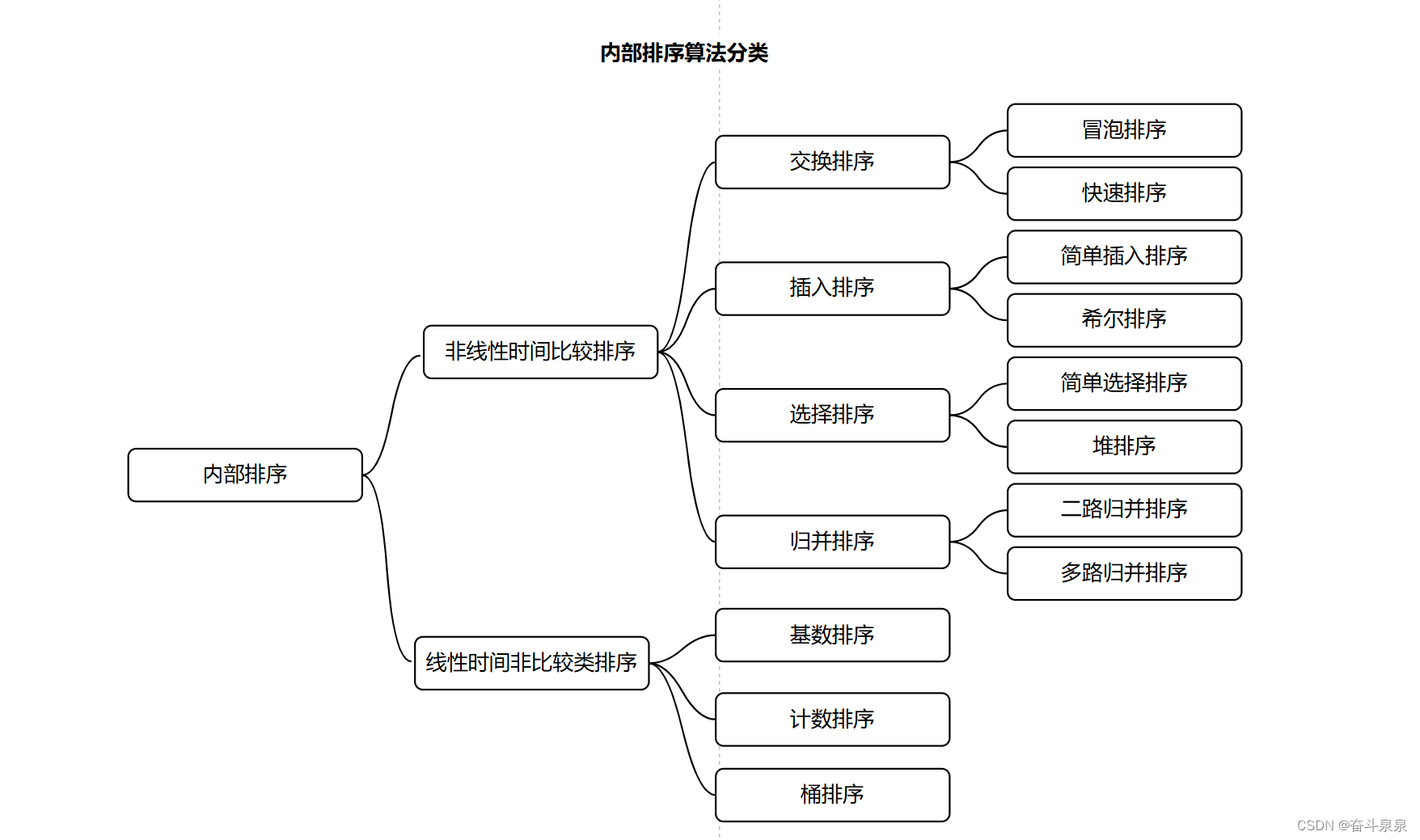
1.3 内部排序算法复杂度
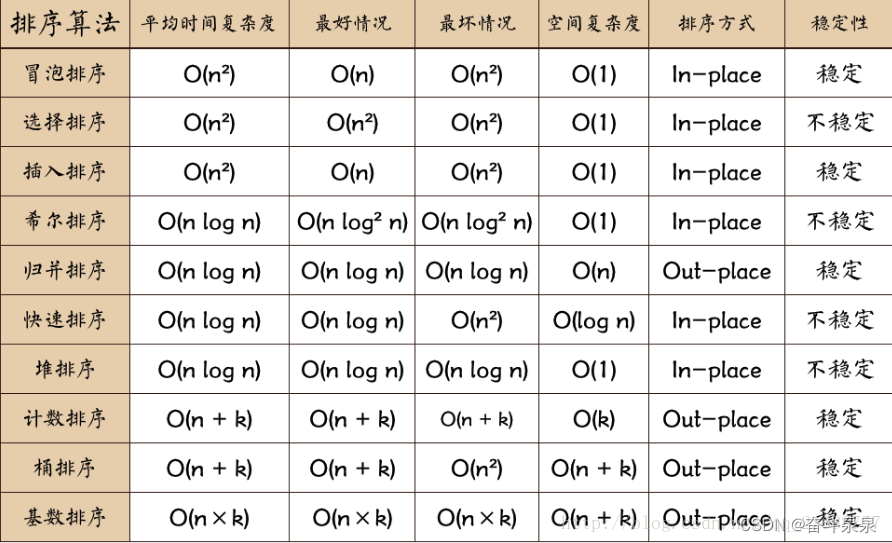
(一) 冒泡排序
冒泡排序,从下往上遍历,每次遍历往上固定一个最小值
添加一个标志位,当某次冒泡排序没有元素交换时,则冒泡结束,元素已经有序,可以有效减少冒泡次数。
public class BubbleSort{
public int [] bubbleSort(int []Arr,int n)
{
//以flag为标记,标记数组是否已经排序完成
boolean flag = true;
//固定左边的数字
for(int i=0;i<n-1&flag;i++)
{
flag = false;
//从后面(下面)往前(上)遍历
for(int j=n-2;j>=i;j--)
{
if(A[j]>A[j+1])
{
swap(A,j,j+1);
flag = true;
}
}
}
return A;
}
//数组是按引用传递,在函数中改变数组起作用
private void swap(int []A,int i,int j)
{
int temp = A[i];
A[i] = A[j];
A[j] = temp;
}
}
(二) 简单选择排序
初始升序:交换0次,时间复杂度为O(n);
初始降序:交换n-1次,时间复杂为O(n^2);
特点:交换移动数据次数少,比较次数多。
import java.util.*;
public class Selection{
public int [] selectionSort(int [] A,int n){
//简短选择排序算法,排序结果为递增数组
//记录最小下标值
int min=0;
//固定左边的数字
for(int i=0;i<A.length-1;i++)
{
min=i;
//找到下标i开始后面的最小值
for(int j=i+1;j<A.length;j++)
{
if(A[min]>A[j])
{
min=j;
}
}
//确保稳定排序,数值相等就不用交换
if(i!=min)
{
swap(A,i,min);
}
}
}
return A;
}
private void swap(int []A,int i,int j)
{
int temp = A[i];
A[i]=A[j];
A[j]=temp;
}
(三)直接插入排序
public class InsertionSort{
public int[] insertionSort(int[] A,int n)
{
//用模拟插入扑克牌的思想
//插入的扑克牌
int i, j,temp;
//已经插入一张,继续插入
for(i=1;i<n;i++)
{
temp = A[i];
//把i前面所有大于要插入的牌往后移一位,空出一位给新的牌
for(j=i;j>0&&A[j-1]>temp;j--)
{
A[j]=A[j-1];
}
//把空出来的一位填满插入的牌
A[j] = temp;
}
return A;
}
}
(四) 希尔排序
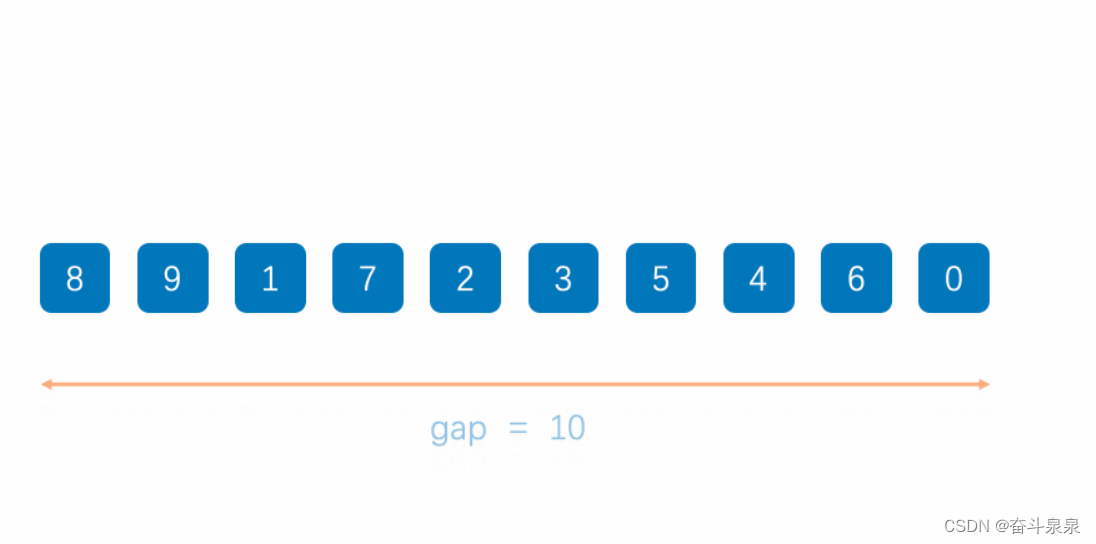
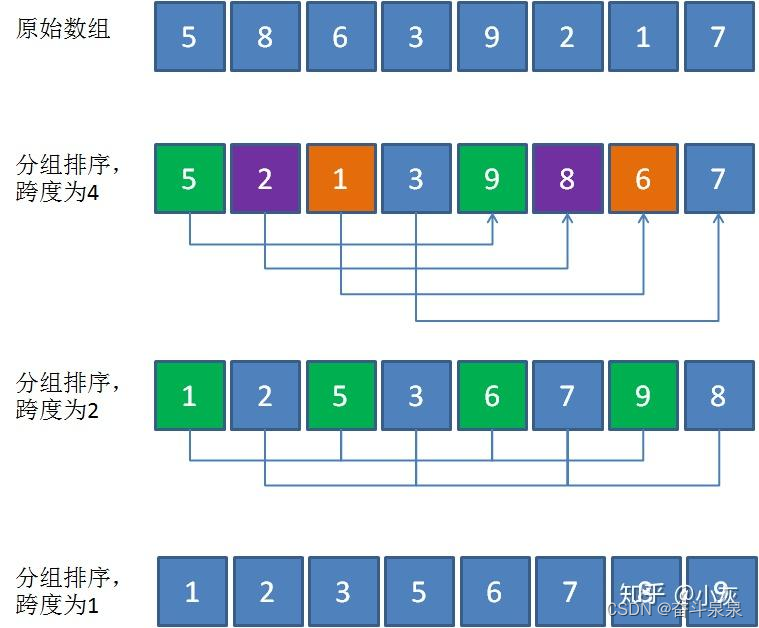
基本思想:算法先将要排序的一组数按某个增量d(n/2,为要排序数的个数)分成若干组,每组中记录的下标相差d,对每组中全部元素进行直接插入排序,然后再用一个较小的增量(d/2)对它进行分组,在每组中再进行直接插入排序。当增量减到一时,进行直接插入排序后,排序完成
希尔排序(缩小增量法)属于插入类排序,是将整个无序列分割成若干小的子序列分别进行插入排序的方法。
import java.util.*;
public class ShellSort{
public int[] shellSort(int []A,int n)
{
//要插入的纸牌
int temp,j,i;
//设定增量D,增量D/2逐渐减小
for(int D =n/2;D>=1;D=D/2)
{
//从下标d开始,对数组d进行插入排序
for(j=D;j<n;j++)
{
temp=A[j];
for(i=j;i>=D&&A[i-D]>temp;i-=D)
{
A[i]=A[i-D];
}
A[i] = temp;
}
}
return A;
}
}
(五) 堆排序
【堆】 1、堆是完全二叉树 2、大顶堆:每个节点的值都大于或等于其左右孩子节点的值,称为大顶堆。3、小顶堆:每个节点的值都大于或等于其左右孩子节点的值,称为小顶堆。
【完全二叉树数组表示形式】:如果i>1,则双亲结点[i/2]。也就是说下标i与下标i2+1是双亲子女关系。
(注意如果排序对象为数组时,下标从0开始,所以下标i与下标21+1和2*i+2是双亲子女关系)
import java.util.*;
public class HeapSort{
public int[] heapSort(int[] A,int n)
{
//堆排序方法
int i;
//先把A[]数组构建成一个大顶堆。
//从完全二叉树的最下层最右边的非终端点开始构建。
for(i=n/2-1;i>=0;i--)
{
HeapAdjust(A,i,n);
}
//开始遍历
for(i=n-1;i>0;i--)
{
swap(A,0,i);
//每交换一次得到一个最大值然后丢弃
HeapAdjust(A,0,i);
}
return A;
}
//A[i] 代表的是下标为i的根节点
private void HeapAdjust(int [] A,int i, int n)
{
//【注意】这里下标从0开始
int temp;
//存储根节点
temp =A[i];
//沿根节点的左右孩子中较大的往下遍历,由于完全二叉树特性i在左子节点2*i+1 i的右子节点 2*i+2
for(int j=2*i+1;j<n;j=j*2+1)
{
if(j<n-1&&A[j]<A[j+1])
{
++j;
}
if(temp>=A[j])
{
break;
}
//将子节点赋值给根节点
A[i]=A[j];
//将子节点下标赋给i
i=j;
}
//将存储的根节点的值赋值给子节点
A[i]=temp;
}
private void swap(int []A,int i,int j)
{
int temp = A[i];
A[i]=A[j];
A[j]=temp;
}
}










![[C++][数据结构][B-树][上]详细讲解](https://img-blog.csdnimg.cn/direct/f53701dadefc49988bf95f91c3ad5c21.png)