1.所有可达路径

98. 所有可达路径 | 代码随想录

代码： （深搜）邻接矩阵表示

#include <iostream>
#include <vector>
using namespace std;
vector<int> path;
vector<vector<int>> result;
void dfs(const vector<vector<int>> &graph,int x,int n){
    // 出口
    if(x == n){ // 当当前遍历结点x为要求终点n时
        result.push_back(path);
        return;
    }
    // 遍历每一个结点
    for(int i = 1; i <= n; i++){
        if(graph[x][i] == 1){
            path.push_back(i);
            dfs(graph,i,n);
            path.pop_back();
        }
    }
}
int main(){
    // 输入
    int n,m,s,t;
    cin >> n >> m;
    // 构造点(结点从1开始编号)
    vector<vector<int>> graph(n + 1,vector<int>(n + 1,0));
    // 构造边
    while(m--){
        cin>>s>>t;
        graph[s][t] = 1;
    }
    // 处理
    path.push_back(1);
    dfs(graph,1,n);
    // 输出
    if(result.size() == 0) cout << -1 <<endl;
   for(const vector<int>&pa:result){
       for(int i = 0;i < pa.size() - 1;i++){
           cout << pa[i] <<" ";
       }
       cout << pa[pa.size() - 1] << endl;
   }
    
}

思路：

这里的深搜的处理方式和之前的回溯法是类似的。

确定函数类型和参数，确定深搜的出口，确定深搜的处理过程（也就是for循环）

易错点：因为邻接矩阵是序号从1开始的，所以在深搜的for循环里要注意边界条件取了等号。

代码：（深搜）邻接表表示 

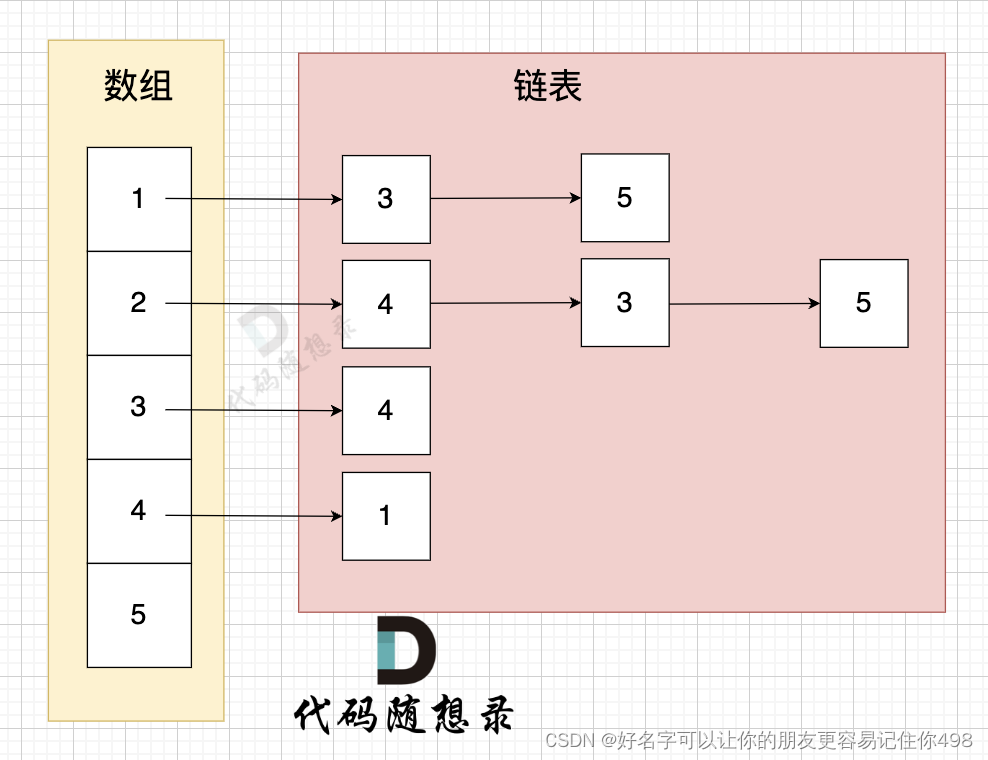
这里表达的图是：

• 节点1 指向 节点3 和 节点5
• 节点2 指向 节点4、节点3、节点5
• 节点3 指向 节点4
• 节点4指向节点1

有多少边 邻接表才会申请多少个对应的链表节点。

从图中可以直观看出 使用 数组 + 链表 来表达 边的连接情况 。

#include <iostream>
#include <vector>
#include <list>
using namespace std;
vector<int> path;
vector<vector<int>> result;
void dfs(const vector<list<int>> &graph,int x,int n){
    if(x == n){
        result.push_back(path);
        return;
    }
    for(int i : graph[x]){
        path.push_back(i);
        dfs(graph,i,n);
        path.pop_back();
    }
}
int main(){
    int n,m,s,t;
    cin >> n >> m;
    // 构造点
    vector<list<int>> graph(n + 1);
    // 构造边
    while(m--){
        cin >> s >> t;
        graph[s].push_back(t);
    }
    
    path.push_back(1);
    dfs(graph,1,n);
    
    if(result.size() == 0) cout << -1 << endl;
    for(const vector<int> &pa:result){
        for(int i = 0; i < pa.size() - 1; i++){
            cout << pa[i] << " ";
        }
        cout << pa[pa.size() - 1] << endl;
    }
}

思路：

易错点：graph是从1开始的，但是result不是，我写成从1开始遍历输出了