目录

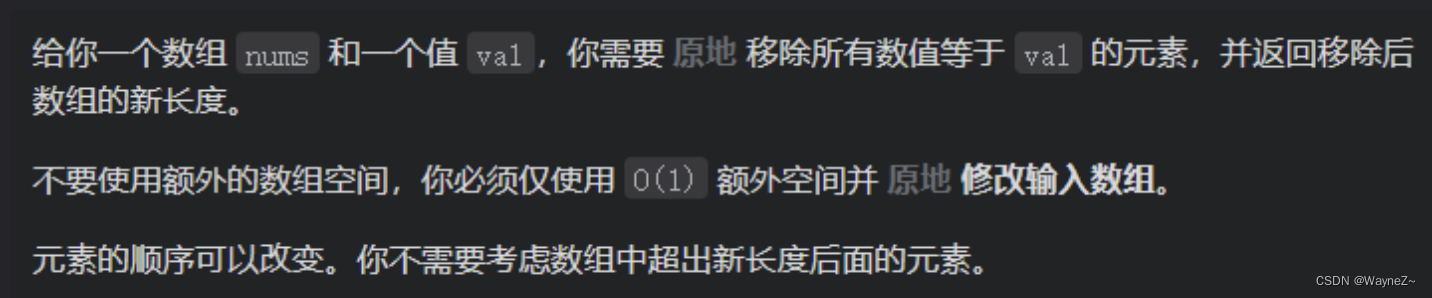
描述

输入描述： 

返回值描述：

示例1 

示例2 

示例3 

思路： 

代码

 

---

描述

给一个长度为n链表，若其中包含环，请找出该链表的环的入口结点，否则，返回null。 

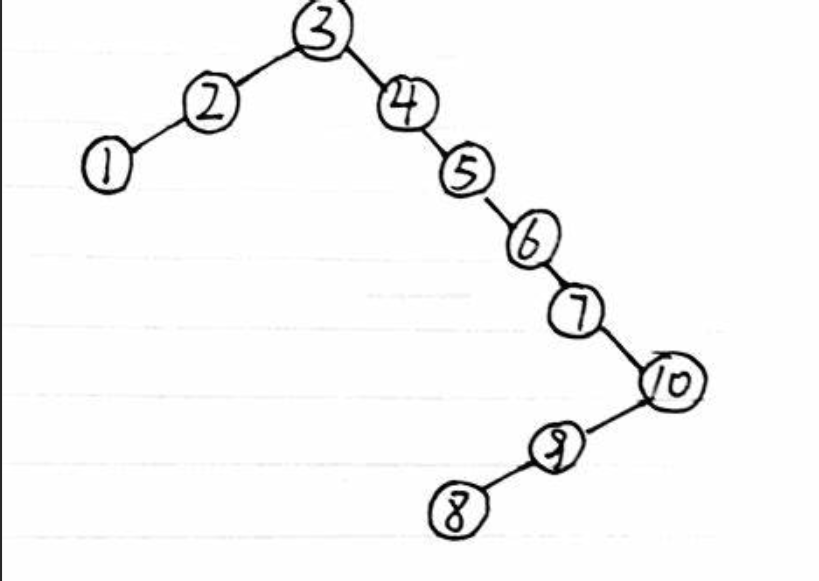
例如，输入{1,2},{3,4,5}时，对应的环形链表如下图所示： 

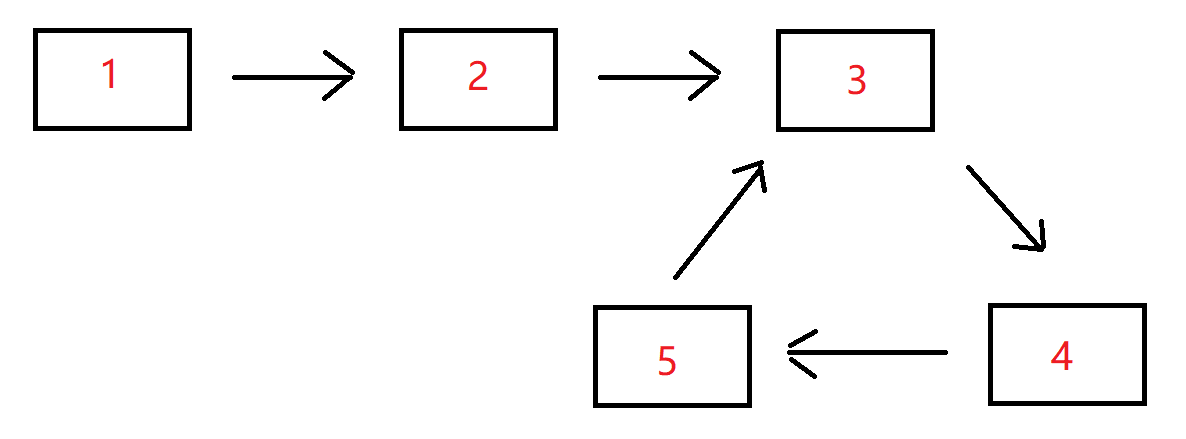
可以看到环的入口结点的结点值为3，所以返回结点值为3的结点。 

输入描述： 

输入分为2段，第一段是入环前的链表部分，第二段是链表环的部分，后台会根据第二段是否为空将这两段组装成一个无环或者有环单链表

返回值描述：

返回链表的环的入口结点即可，我们后台程序会打印这个结点对应的结点值；若没有，则返回对应编程语言的空结点即可。

示例1 

输入：{1,2},{3,4,5}

返回值：3

说明：返回环形链表入口结点，我们后台程序会打印该环形链表入口结点对应的结点值，即3

示例2 

输入：{1},{}

返回值："null"

说明：没有环，返回对应编程语言的空结点，后台程序会打印"null"

示例3 

输入：{},{2}

返回值：2

说明：环的部分只有一个结点，所以返回该环形链表入口结点，后台程序打印该结点对应的结点值，即2

思路： 

刚开始跟那个是否有环搞混了，如果按照那个思路走，你找到快慢指针相同的是相遇的点，不是环的起点

那我们现在假定已经是一个有环的链表了，那么这个链表中怎么找到环的入口呢？在慢指针进入链表环之前，快指针已经进入了环，且在里面循环，这才能在慢指针进入环之后，快指针追到了慢指针，不妨假设快指针在环中走了nnn圈，慢指针在环中走了mmm圈，它们才相遇，而进入环之前的距离为xxx，环入口到相遇点的距离为yyy，相遇点到环入口的距离为zzz。快指针一共走了x+n(y+z)+yx+n(y+z)+yx+n(y+z)+y步，慢指针一共走了x+m(y+z)+yx+m(y+z)+yx+m(y+z)+y，这个时候快指针走的倍数是慢指针的两倍，则x+n(y+z)+y=2(x+m(y+z)+y)x+n(y+z)+y=2(x+m(y+z)+y)x+n(y+z)+y=2(x+m(y+z)+y)，这时候x+y=(n−2m)(y+z)x+y=(n-2m)(y+z)x+y=(n−2m)(y+z)，因为环的大小是y+zy+zy+z，说明从链表头经过环入口到达相遇地方经过的距离等于整数倍环的大小：那我们从头开始遍历到相遇位置，和从相遇位置开始在环中遍历，会使用相同的步数，而双方最后都会经过入口到相遇位置这yyy个节点，那说明这yyy个节点它们就是重叠遍历的，那它们从入口位置就相遇了，这我们不就找到了吗？

后面可以推出 x+y = nl，这里面l是整个圈的长度，y+z = l，可以推出x = (n - 1)l + z，所以说如果相遇肯定在交叉起点

代码

public ListNode EntryNodeOfLoop(ListNode pHead) {
        ListNode fast = pHead;
        ListNode slow = pHead;

        ListNode yu = null;

        while (fast != null && fast.next != null) {
            fast = fast.next.next;
            slow = slow.next;
            if (fast == slow) {
                yu = slow;
                slow = pHead;
                while (yu != slow) {
                    yu = yu.next;
                    slow = slow.next;

                }
                break;
            }

        }
        return yu;
    }