傅里叶级数在不连续点会怎么样？？？

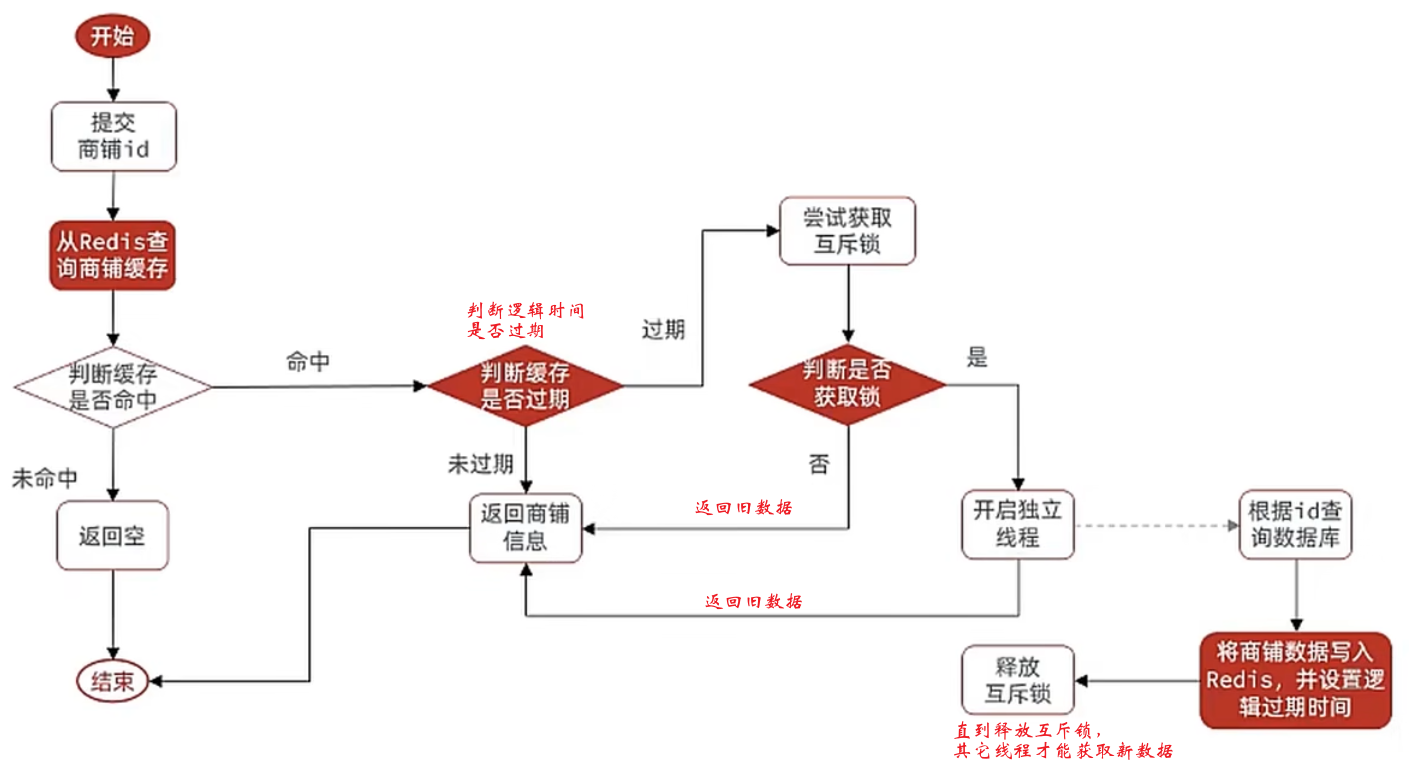
文章目录

一、前言背景
二、用狄利克雷核表达傅里叶级数
三、狄利克雷核与狄拉克函数
四、傅里叶级数在不连续点的表示
五、吉伯斯现象的解释
六、总结
参考资料

一、前言背景

笔者最近在撸《信号与系统》，写下此博客用作记录和分享学习笔记。由于是笔者为电子爱好者，不是数学专业从事人员，如有不对还望各网友大神指正。本博客大量借鉴资料，笔者只是拾人牙慧的小屁孩。
笔者在学习傅里叶级数或者傅里叶变换时，对傅里叶级数或是傅里叶变换的收敛性颇有疑问。
有狄利克雷条件约束：

在任何周期内， $x (t)$ 必须绝对可积（ $\int_{T}{|x(t)|}dt < \infty$ ），以此保证傅里叶级数系数 $a_{k}$ 都是有限值：
$|a_{k}| \leq \frac{1}{T} \int_{T} |x(t)e^{-jkw_{0}t}|dt = \frac{1}{T} \int_{T} |x(t)|dt < \infty$
在任意有限区间内， $x (t)$ 具有有限个起伏变化；也就是说，在任何单个周期内， $x (t)$ 的最大值和最小值的数目有限。
在任意有限区间内，只有有限个不连续点，而且在这些不连续点上，函数是有限值。

其中说到，对于一个周期内存在的有限数目的不连续点的周期信号而言，除去那些孤立的不连续点外，其余所有点上傅里叶级数都等于原来的 $x (t)$ ；而在那些孤立的不连续点上，傅里叶级数收敛于不连续点处的平均值。

这句话令笔者十分疑惑——傅里叶级数还能对不连续的信号的进行处理？
按照道理说，傅里叶级数由正弦和余弦函数构成，这些函数本质上是平滑的、连续的，怎么能表达不连续的信号呢？
于是我们展开下文…

二、用狄利克雷核表达傅里叶级数

我们都知道一个周期信号可以被傅里叶级数展开，
$\sum\limits_{k = -\infty}^{+\infty}a_{k}e^{jkw_{0}t}$
对于存在不连续点的 $x (t)$ ，我们似乎难以下手，只能使用极限的知识。
现在以一个方波为例，
$x(t)=\left\{ \begin{aligned} 1 , & |t| < T_{1}\\ 0 , & T_{1} < |t| < \frac{T}{2} \end{aligned} \right.$
我们对 $T_{1}$ 处取极限，
$\lim \limits_{t \rightarrow T_{1}} x(t) = \lim \limits_{t \rightarrow T_{1}} \sum\limits_{k = -\infty}^{+\infty}a_{k}e^{jkw_{0}t} = \sum\limits_{k = -\infty}^{+\infty}a_{k}e^{jkw_{0} T_{1}}$
我们可以发现，由于这个方波满足狄利克雷条件，求和（ $\sum\limits_{k = -\infty}^{+\infty}$ ）以及傅里叶级数系数（ $a_{k}$ ）都收敛，故 $\lim \limits_{t \rightarrow T_{1}} x(t) < \infty$ 。（当然， $\lim \limits_{t \rightarrow T_{1}^{-}} x(t) = 0$ ， $\lim \limits_{t \rightarrow T_{1}^{+}} x(t) = 1$ ）

这真是一个amazing的结果，这说明一个满足狄利克雷条件的周期信号，本来有不连续点，但利用傅里叶级数展开式可以得到其收敛值。
我们尝试计算：
$\begin{aligned} x(t) & = \sum\limits_{k = -\infty}^{+\infty}a_{k}e^{jkw_{0}t} \\ x(t) & = \sum\limits_{k = -\infty}^{+\infty}(\frac{1}{T}\int_{T}x(\tau)e^{-jkw_{0}\tau}d\tau)e^{jkw_{0}t} \\ x(t) & = \frac{1}{T} \int_{T} x(\tau) \sum\limits_{k = -\infty}^{+\infty}e^{jkw_{0}(t -\tau)}d\tau \end{aligned}$

这里我们引入狄利克雷核：
$\begin{aligned} D_{N}(t) = \sum\limits_{k = -N}^{+N}e^{jkt} &= \sum\limits_{k = -N}^{+N} (\cos (kt) + j \sin (kt)) \\ &= \sum\limits_{k = -N}^{+N} \cos (kt) + j \sum\limits_{k = -N}^{-1} \sin (kt)+ j \sum\limits_{k = 1}^{N} \sin (kt) + j \sin (0)\\ &= \sum\limits_{k = -N}^{+N} \cos (kt) + j \sum\limits_{k = 1}^{N} \sin (-kt)+ j \sum\limits_{k = 1}^{N} \sin (kt) + 0\\ &= \sum\limits_{k = -N}^{+N} \cos (kt) - j \sum\limits_{k = 1}^{N} \sin (kt)+ j \sum\limits_{k = 1}^{N} \sin (kt) \\ &= \sum\limits_{k = -N}^{+N} \cos (kt) \\ \end{aligned}$
又因为 $\sin \alpha \cos \beta = \sin ( \alpha + \beta) + \sin ( \alpha - \beta)$ ，
我们有
$\begin{aligned} 2 \sin (\frac{t}{2}) \cos (kt) &= \sin (\frac{t}{2} + kt) + \sin (\frac{t}{2} - kt) \\ \sum\limits_{k = -N}^{+N} 2 \sin (\frac{t}{2}) \cos (kt) &= \sum\limits_{k = -N}^{+N} \sin (\frac{t}{2} + kt) + \sin (\frac{t}{2} - kt) \\ \sum\limits_{k = -N}^{+N} 2 \sin (\frac{t}{2}) \cos (kt) &= \sum\limits_{k = -N}^{+N} \sin (kt + \frac{t}{2}) - \sin (kt - \frac{t}{2}) \\ \sum\limits_{k = -N}^{+N} 2 \sin (\frac{t}{2}) \cos (kt) &= [\sin (- Nt + \frac{t}{2}) - \sin (-Nt -\frac{t}{2}) +\sin (- (N-1)t + \frac{t}{2}) - \sin (-(N-1)t -\frac{t}{2}) + ... + 2 \sin (\frac{t}{2}) + ... + \sin (Nt + \frac{t}{2}) - \sin (Nt -\frac{t}{2})] \\ \sum\limits_{k = -N}^{+N} 2 \sin (\frac{t}{2}) \cos (kt) &= - \sin (-Nt -\frac{t}{2}) - \sin (\frac{t}{2}) + 2 \sin (\frac{t}{2}) + \sin (Nt + \frac{t}{2}) - \sin (\frac{t}{2}) \\ \sum\limits_{k = -N}^{+N} 2 \sin (\frac{t}{2}) \cos (kt) &= 2 \sin (Nt +\frac{t}{2}) \\ \sum\limits_{k = -N}^{+N} \cos (kt) &= \frac{ 2 \sin (Nt +\frac{t}{2})}{2 \sin (\frac{t}{2}) } \\ \sum\limits_{k = -N}^{+N} \cos (kt) &= \frac{ \sin ((N + \frac{1}{2})t)}{ \sin (\frac{t}{2}) } \end{aligned}$

故，我们可以得出狄利克雷核的表达式为：
$D_{N}(t) = \sum\limits_{k = -N}^{+N}e^{jkt} = \sum\limits_{k = -N}^{+N} \cos (kt) = \frac{ \sin ((N + \frac{1}{2})t)}{ \sin (\frac{t}{2}) }$
我们重新看回傅里叶级数表达的 $x (t)$ ，用狄利克雷核表达也就是：
$\begin{aligned} x(t) & = \frac{1}{T} \int_{T} x(\tau) \sum\limits_{k = -\infty}^{+\infty}e^{jkw_{0}(t -\tau)}d\tau \\ x(t) & = \frac{1}{T} \int_{T} x(\tau) D_N(w_{0}(t-\tau)) d\tau \end{aligned}$
其中 $\rightarrow \infty$ 。
我们可以发现， $x (t)$ 的傅里叶级数展开又可以看作和狄利克雷核作周期卷积。

三、狄利克雷核与狄拉克函数

上文提到的 $x (t)$ 的傅里叶级数展开可以表达为 $x (t)$ 自己和狄利克雷核（ $\rightarrow \infty$ 时）作周期卷积，于是我们对狄利克雷核展开研究，看看是否具有什么优秀的性质能够简化我们的卷积计算。

使用MATLAB绘制狄利克雷核的图像：

N = 10;
t = -5 : 0.000001 : 5;
x = sin((N + 0.5) * t) ./ (t * 0.5);

plot(t, x);
title("Dirichlet Kernel (N = " + N + ")");

调节N系数绘制图形：

N = 10 :

Dirchlet (N = 10)

N = 100 :

Dirchlet (N = 100)

N = 100000 :

Dirchlet (N = 100000)

可以看出狄利克雷核在 $N$ 越大，其性质越像狄拉克函数 $\delta(t)$ ：
$\lim \limits_{t \rightarrow 0} D_{N}(t)= 2N + 1$
而且
$\int_{T} D_{N}(w_{0}t)dt = \int_{T} \sum\limits_{k = -N}^{+N}e^{jkw_{0}t}dt =\sum\limits_{k = -N}^{+N} \int_{T} e^{jkw_{0}t}dt$
而 $\int_{T} e^{jkw_{0}t}dt$ 仅在 $k = 0$ 时不为零，
故，我们可推出，
$\int_{T} D_{N}(w_{0}t)dt = \int_{T} dt = T$
这两条推论可以得出： $N$ 越大，狄利克雷核在 $0$ 处的趋于值越大（ $2 N + 1$ ）；狄利克雷核在一个周期积分其值固定（ $T$ ）。
我们推理，当 $\rightarrow \infty$ ，狄利克雷核在 $0$ 处也趋于 $\infty$ ，但是由于狄利克雷核在一个周期积分其值固定为 $T$ ，所以相当于全部的能量都聚集到了 $0$ 处，性质十分类似狄拉克函数 $\delta(t)$ 。

比如就可以说，当 $\rightarrow \infty$ ， $\int_{T} x(t)D_{N}(w_{0}t)dt = Tx(0)$ 。

四、傅里叶级数在不连续点的表示

刚刚我们知道了狄利克雷核在 $\rightarrow \infty$ 下的性质近似狄拉克函数的性质，于是我们重新看回我们之前提到的 $x (t)$ 的傅里叶级数展开可以表达为 $x (t)$ 自己和狄利克雷核（ $\rightarrow \infty$ 时）的周期卷积。
当 $\rightarrow \infty$ 时，不存在不连续点时，
$\begin{aligned} x(t) & = \lim \limits_{N \rightarrow \infty} \frac{1}{T} \int_{T} x(\tau) D_N(w_{0}(t-\tau)) d\tau = \frac{1}{T} \cdot T x(t) = x(t) \end{aligned}$
可以发现，傅里叶级数展开式 $x (t)$ 就是其 $x (t)$ 本身。

而存在不连续点（ $t_{0}$ ）时，我们就改变积分区间，去掉不连续点处（不连续点实际上是一个点，那么它对应的面积是一条线的面积也就是 $0$ ，因此，不连续点对面积的影响可以忽略不计），
$\begin{aligned} x(t_{0}) & = \lim \limits_{N \rightarrow \infty} \frac{1}{T} \int_{-\frac{T}{2}}^{t_{0} - \varepsilon } x(\tau) D_N(w_{0}(t_{0}-\tau)) d\tau + \lim \limits_{N \rightarrow \infty} \frac{1}{T} \int_{t_{0} + \varepsilon}^{\frac{T}{2}} x(\tau) D_N(w_{0}(t_{0}-\tau)) d\tau \\ &= \frac{1}{T} \cdot \frac{T}{2} x(t_{0}^{-}) + \frac{1}{T} \cdot \frac{T}{2} x(t_{0}^{+})\\ &= \frac{ x(t_{0}^{-}) + x(t_{0}^{+})}{2} \end{aligned}$
最后我们得出，满足狄利克雷条件的周期函数，在其不连续点处会趋于不连续点的平均值。

将方波傅里叶级数展开后，再以对应的 $N$ 画出其对应的有限项近似 $x_{N}(t)$ 。
对于任意的 $N$ 来说， $x_{N}(t)$ 在不连续点都为该点平均值。
方波傅里叶级数的收敛

五、吉伯斯现象的解释

不过，在时域上有趣的现象不仅是满足狄利克雷条件的周期函数，在其不连续点处会趋于不连续点的平均值，还有当傅里叶级数为有限项的傅里叶级数截断近似时，在不连续点处呈现的起伏。

对于一周期方波，
$x(t)=\left\{ \begin{aligned} 1 , & |t| < T_{1}\\ 0 , & T>|t| > T_{1} \end{aligned} \right.$

其傅里叶级数为
$a_{k} =\frac{sin(kw_{0}T_{1})}{k \pi}$

我们编写MATLAB代码，模拟有限项求和傅里叶级数的结果：

N = 50;

T = 2 * pi; 
w0 = 2 * pi / T;
t = -3:0.00001:3;
T1 = 1;

y = (abs(t) < T1);

x = zeros(size(t));

for k = -N:N
    if k == 0
        ak = w0 * T1 / pi;
    else
        ak = (sin(k * w0 * T1)) / (k * pi);
    end
    
    x = x + ak * exp(1j * k * w0 * t);
end

hold on;
plot(t, real(x), 'b');
plot(t, y);
title("N = " + N);
hold off;

[max_value, max_index] = max(real(x));
overshoot = (max_value - 1) / 1 * 100; 
disp(['Maximum value: ', num2str(max_value)]);
disp(['Overshoot percentage: ', num2str(overshoot), '%']);

N=10有限项傅里叶级数

N=50有限项傅里叶级数
N=500有限项傅里叶级数

可以发现随着 N 的变大不连续点起伏的峰值大小没有改变太多，始终存在过冲，并没有随着N 的变大而下降。

这原因可以追溯到狄利克雷核中，虽然随着 N 的变大，狄利克雷核的性质越来越类似狄拉克函数 $\delta(t)$ 的性质，但其图像却很有自己的特色。
狄利克雷核的图形由一个主要的中心峰（主瓣）和多对对称的较小振荡（旁瓣）组成。主瓣的高度随着 N 的增大而增大，旁瓣则在靠近 $t = 0$ 处密集振荡。旁瓣的振幅虽然逐渐减小，但振荡的频率随 N 的增大而增大。狄利克雷核的积分贡献主要来自主瓣的中心区域以及旁瓣的高频振荡。
当 $t_{0}$ 是连续点时，积分结果会随着 $N$ 的增大逐渐逼近 $x(t_{0})$ 。（ $\lim \limits_{N \rightarrow \infty} \frac{1}{T} \int_{T} x(\tau) D_N(w_{0}(t-\tau)) d\tau$ 趋于 $x (t)$ ）狄利克雷核的主瓣捕捉到了主要变化，旁瓣的高频成分对平滑变化的函数影响较小。（可以想象狄利克雷核卷积的过程，由于连续点周围的点都变化不大，当 $N$ 很大时，旁瓣的影响十分细微）
但是当 $t_{0}$ 是不连续点时，这个积分结果将很受旁瓣的高频振荡的影响，（因为不连续点周围的点变化很大，导致这个振荡表现得更加明显），出现过冲。（资料上说这个过冲将会有 $9$ %，且不随 $N$ 的增大而下降）

编写MATLAB代码，实现对连续信号和不连续信号分别对狄利克雷核的周期卷积：

N = 50;
t = -pi:0.00001:pi;

D_N = sin((N + 0.5) * t) ./ (0.5 * t);
D_N(t == 0) = (N + 0.5) / 0.5;

figure;
plot(t, D_N);
title("D_N(t) N = " + N);

x1 = cos(t);
x2 = (abs(t) < pi/2);


y1 = conv(x1, D_N, 'same') * (t(2) - t(1)) / ( 2 * pi);

y2 = conv(x2, D_N, 'same') * (t(2) - t(1)) / ( 2 * pi);


figure;
subplot(2, 1, 1);
plot(t, x1, 'b');
hold on;
plot(t, y1, 'r');

subplot(2, 1, 2);
plot(t, x2, 'b');
hold on;
plot(t, y2, 'r');

D_N(t) N = 50
连续信号和不连续信号
可以发现，信号在连续点受旁瓣影响小，在不连续点受旁瓣影响大。
随着 $N$ 变大，只是让旁瓣向着 $t = t_{0}$ 压缩。对于不连续点 $t_{0}$ 处，也就是随着 $N$ 变大，不连续点受旁瓣影响导致的振荡会向着 $t = t_{0}$ 压缩。
从能量的角度来说，当不连续点附近的振荡被压缩时，由于能量守恒，不连续点处的过冲会增加。只不过由于狄利克雷核随 $N$ 增大到一定程度后，旁瓣在纵轴变化的程度不大，故过冲在 $N$ 增大到一定程度后变化幅度也很小。
吉伯斯效应是一个典型的受狄利克雷核影响的现象，狄利克雷核还有很多有趣的性质等待人们挖掘。

六、总结

$x (t)$ 的傅里叶级数的展开式可以看作 $x (t)$ 与狄利克雷核做周期卷积的结果。我们探索狄利克雷核的各种性质（比如其类似狄拉克函数 $\delta(t)$ 的性质），从而探索傅里叶级数的各种性质。狄利克雷核在周期积分为定值，且在 $t = 0$ 处的趋近值随 $N$ 变大而变大。不同的 $N$ 值让狄利克雷核的主瓣和旁瓣不同程度地影响着傅里叶级数。