数据分析中的数学:从基础到应用
数据分析离不开数学的支持,统计学和概率论是其重要组成部分。本文将通过几个具体的实例,详细讲解数据分析中常用的数学知识,并通过Python代码演示如何应用这些知识。
1. 描述性统计
基本概念和用途
描述性统计用于总结和描述数据的特征,包括集中趋势和离散程度的度量。
- 均值(Mean):所有数据的平均值,表示数据的中心位置。例如,在分析学生成绩时,均值可以告诉我们班级的平均成绩。
- 中位数(Median):数据排序后中间的值,适用于有极端值的数据。例如,分析家庭收入时,中位数比均值更能代表典型收入。
- 众数(Mode):数据中出现次数最多的值,适用于分类数据。例如,分析最常见的产品类型。
- 方差(Variance)和标准差(Standard Deviation):表示数据的离散程度,方差为数据偏离均值的程度,标准差为方差的平方根。例如,标准差可以告诉我们学生成绩的离散程度。
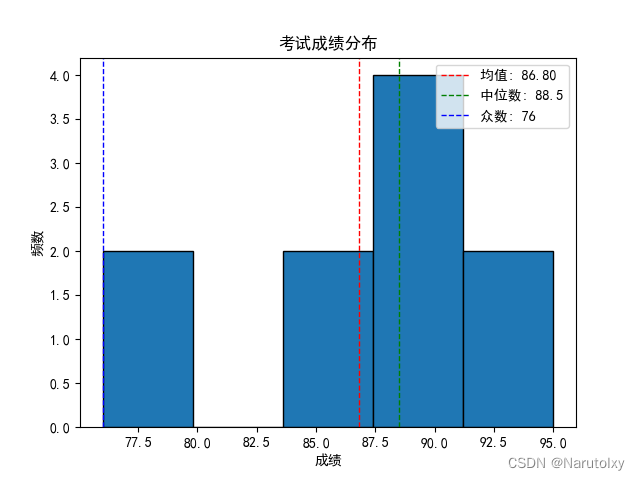
实例:分析班级学生的考试成绩
假设我们有一组学生的考试成绩,分别为:85, 90, 78, 92, 88, 76, 95, 89, 84, 91。我们希望了解这些成绩的集中趋势和离散程度。
Python代码示例
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
# 设置中文字体
plt.rcParams['font.sans-serif'] = ['SimHei'] # 用于Windows
plt.rcParams['axes.unicode_minus'] = False # 解决坐标轴负号显示问题
# 创建数据
scores = [85, 90, 78, 92, 88, 76, 95, 89, 84, 91]
# 计算描述性统计量
mean_score = np.mean(scores)
median_score = np.median(scores)
mode_score = pd.Series(scores).mode()[0]
variance_score = np.var(scores)
std_dev_score = np.std(scores)
# 打印结果
print(f"均值: {mean_score}")
print(f"中位数: {median_score}")
print(f"众数: {mode_score}")
print(f"方差: {variance_score}")
print(f"标准差: {std_dev_score}")
# 可视化
plt.hist(scores, bins=5, edgecolor='black')
plt.axvline(mean_score, color='r', linestyle='dashed', linewidth=1, label=f'均值: {mean_score:.2f}')
plt.axvline(median_score, color='g', linestyle='dashed', linewidth=1, label=f'中位数: {median_score}')
plt.axvline(mode_score, color='b', linestyle='dashed', linewidth=1, label=f'众数: {mode_score}')
plt.legend()
plt.title('考试成绩分布')
plt.xlabel('成绩')
plt.ylabel('频数')
plt.show()
2. 推断统计
基本概念和用途
推断统计通过样本数据推断总体特征,常用方法包括估计和假设检验。
- 抽样理论:从总体中随机抽取样本,用样本统计量推断总体参数。例如,从一大群学生中抽取一小部分进行调查,以推断整个学生群体的情况。
- 估计:使用样本数据对总体参数进行估计,包括点估计(一个值)和区间估计(一个范围)。例如,估计班级平均成绩为80分,置信区间为75-85分。
- 假设检验:通过统计检验判断样本数据是否支持某个假设。例如,假设某班级学生的平均成绩等于80分,然后使用样本数据进行检验。
实例:检验某班级学生的平均成绩是否等于80分
假设我们有一组学生的考试成绩,分别为:85, 90, 78, 92, 88, 76, 95, 89, 84, 91。我们希望检验该班级学生的平均成绩是否等于80分。
Python代码示例
import scipy.stats as stats
# 创建数据
sample_scores = [85, 90, 78, 92, 88, 76, 95, 89, 84, 91]
popmean = 80 # 假设总体均值为80
# 单样本t检验
t_statistic, p_value = stats.ttest_1samp(sample_scores, popmean)
# 打印结果
print(f"t统计量: {t_statistic}")
print(f"p值: {p_value}")
# 检验结果
alpha = 0.05
if p_value < alpha:
print("拒绝原假设:班级学生的平均成绩不等于80分")
else:
print("无法拒绝原假设:班级学生的平均成绩等于80分")
在这个例子中,我们使用单样本t检验来检验班级学生的平均成绩是否等于80分。t统计量和p值帮助我们判断是否拒绝原假设。
3. 置信区间
基本概念和用途
置信区间用于估计总体参数的范围,并以一定的置信水平表示该范围包含总体参数的概率。
- 置信区间:基于样本数据计算的总体参数的区间估计。例如,班级平均成绩的95%置信区间为75-85分,这意味着我们有95%的信心认为总体平均成绩在75到85之间。
实例:计算班级学生平均成绩的置信区间
假设我们有一组学生的考试成绩,分别为:85, 90, 78, 92, 88, 76, 95, 89, 84, 91。我们希望计算该班级学生平均成绩的95%置信区间。
Python代码示例
import numpy as np
import scipy.stats as stats
# 创建数据
sample_scores = [85, 90, 78, 92, 88, 76, 95, 89, 84, 91]
sample_mean = np.mean(sample_scores)
sample_std = np.std(sample_scores, ddof=1)
n = len(sample_scores)
# 计算95%置信区间
confidence_level = 0.95
alpha = 1 - confidence_level
t_critical = stats.t.ppf(1 - alpha/2, df=n-1)
margin_of_error = t_critical * (sample_std / np.sqrt(n))
confidence_interval = (sample_mean - margin_of_error, sample_mean + margin_of_error)
# 打印结果
print(f"样本均值: {sample_mean}")
print(f"置信区间: {confidence_interval}")
在这个例子中,我们计算了班级学生平均成绩的95%置信区间。置信区间提供了一个范围,表示我们有95%的信心认为总体平均成绩在这个范围内。
4. 回归分析
基本概念和用途
回归分析用于研究自变量和因变量之间的关系,常用方法包括线性回归和非线性回归。
- 线性回归:通过线性关系预测因变量。例如,使用学习时间预测考试成绩。
- 非线性回归:通过非线性关系预测因变量。例如,使用学习时间预测考试成绩,但关系不是线性的。
- 模型评估:R²、调整R²、残差分析等,评估模型的拟合程度。例如,R²告诉我们自变量解释了多少因变量的变异。
实例:使用学习时间预测考试成绩
假设我们有一组学生的学习时间和相应的考试成绩,学习时间(小时)分别为:2, 3, 4, 5, 6, 7, 8, 9, 10,考试成绩分别为:70, 75, 78, 82, 85, 88, 90, 92, 95。我们希望建立学习时间与考试成绩之间的线性关系模型。
Python代码示例
from sklearn.linear_model import LinearRegression
# 创建数据
study_hours = np.array([2, 3, 4, 5, 6, 7, 8, 9, 10]).reshape(-1, 1)
scores = np.array([70, 75, 78, 82, 85, 88, 90, 92, 95])
# 线性回归模型
model = LinearRegression()
model.fit(study_hours, scores)
# 预测
predictions = model.predict(study_hours)
# 打印回归系数
print(f"回归系数: {model.coef_[0]}")
print(f"截距: {model.intercept_}")
# 可视化
plt.scatter(study_hours, scores, color='blue')
plt.plot(study_hours, predictions, color='red', linewidth=2)
plt.title
('学习时间与成绩之间的线性回归')
plt.xlabel('学习时间(小时)')
plt.ylabel('成绩')
plt.show()
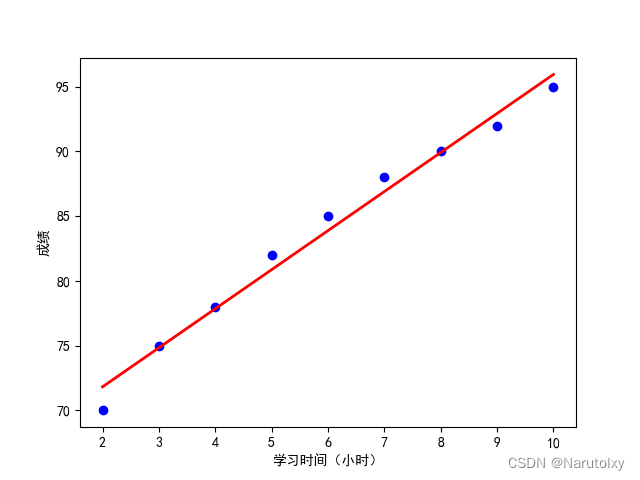
在这个例子中,我们使用线性回归模型来预测学生的考试成绩。回归系数和截距帮助我们了解学习时间与考试成绩之间的关系。
5. 时间序列分析
基本概念和用途
时间序列分析用于分析时间序列数据的模式和趋势,常用方法包括平稳性检验、季节性分解和ARIMA模型。
- 平稳性:时间序列的统计特性不随时间变化。例如,股票价格波动是否有规律。
- 季节性:时间序列的周期性波动。例如,销售额在某些月份会更高。
- 趋势:时间序列的长期上升或下降。例如,长期销售额的增长趋势。
实例:分析某商店的月度销售数据
假设我们有某商店的月度销售数据,从2020年1月到2021年12月。我们希望分析销售数据的趋势和季节性,并预测未来几个月的销售额。
Python代码示例
import pandas as pd
from statsmodels.tsa.seasonal import seasonal_decompose
from statsmodels.tsa.arima.model import ARIMA
# 创建数据
dates = pd.date_range(start='2020-01', periods=24, freq='M')
sales = [265, 278, 289, 302, 310, 320, 330, 350, 370, 390, 405, 420, 430, 440, 460, 480, 500, 520, 540, 560, 580, 600, 620, 640]
data = pd.Series(sales, index=dates)
# 时间序列分解
decomposition = seasonal_decompose(data, model='additive')
decomposition.plot()
plt.show()
# ARIMA模型
model = ARIMA(data, order=(1, 1, 1))
fit_model = model.fit()
# 预测
forecast = fit_model.forecast(steps=6)
print(forecast)
# 可视化
data.plot(label='历史数据', legend=True)
forecast.plot(label='预测数据', legend=True)
plt.title('销售额时间序列分析与预测')
plt.xlabel('日期')
plt.ylabel('销售额')
plt.show()
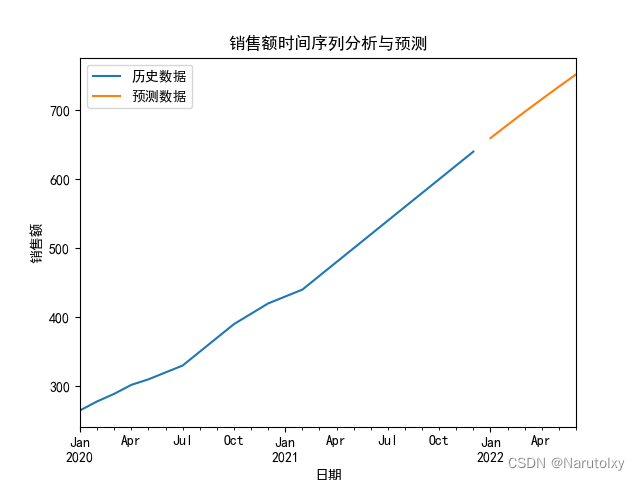
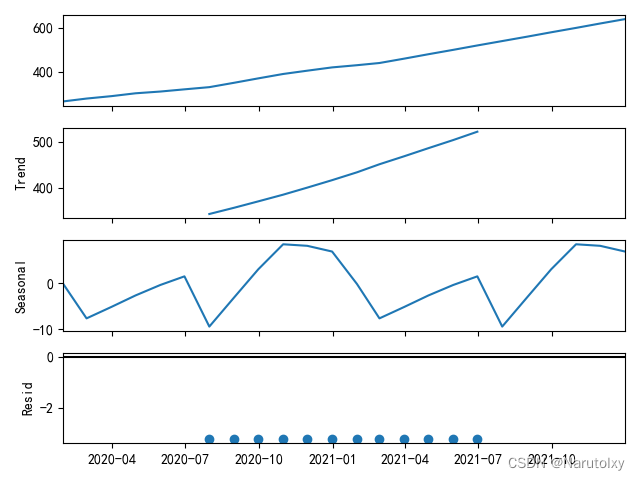
在这个例子中,我们使用时间序列分解方法来分析销售数据的趋势和季节性,并使用ARIMA模型进行预测。
6. 概率论
基本概念和用途
概率论用于研究随机现象的数学理论,常用概念包括随机变量、概率分布和期望值。
- 随机变量:取值不确定的变量。例如,掷骰子的结果。
- 概率分布:描述随机变量取值的可能性。例如,骰子各面朝上的概率。
- 期望值和方差:反映随机变量的平均取值和离散程度。例如,掷骰子的期望值为3.5,方差表示结果的波动性。
实例:分析掷骰子的结果
假设我们要分析掷10次骰子的结果,每次成功(掷出6)的概率为1/6。我们希望了解结果的概率分布。
Python代码示例
import numpy as np
import matplotlib.pyplot as plt
import scipy.stats as stats
# 二项分布
n, p = 10, 1/6 # 进行10次实验,每次成功概率为1/6
binom_dist = stats.binom(n, p)
# 概率质量函数(PMF)
x = np.arange(0, n+1)
pmf = binom_dist.pmf(x)
# 可视化
plt.bar(x, pmf)
plt.title('二项分布的概率质量函数')
plt.xlabel('成功次数')
plt.ylabel('概率')
plt.show()
# 正态分布
mu, sigma = 0, 1 # 均值为0,标准差为1
norm_dist = stats.norm(mu, sigma)
# 概率密度函数(PDF)
x = np.linspace(-3, 3, 100)
pdf = norm_dist.pdf(x)
# 可视化
plt.plot(x, pdf)
plt.title('正态分布的概率密度函数')
plt.xlabel('值')
plt.ylabel('概率密度')
plt.show()
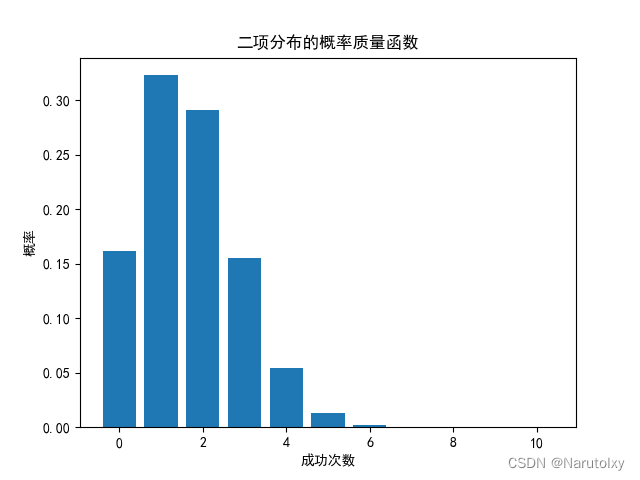
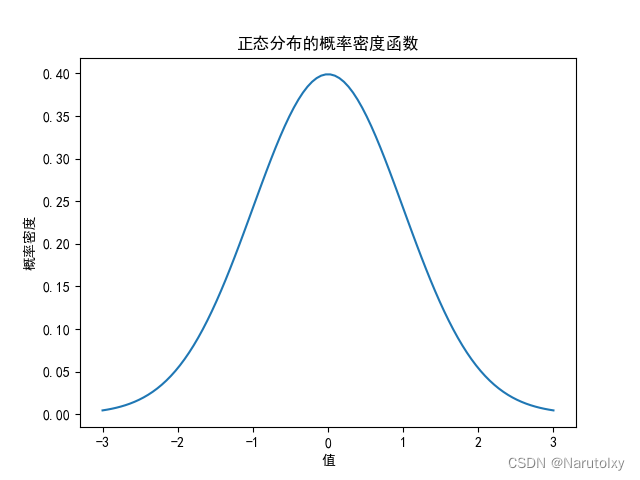
在这个例子中,我们分析了掷骰子的结果,使用二项分布描述掷10次骰子成功(掷出6)的概率,并使用正态分布描述某些连续随机变量的概率密度。
通过这些具体和生动的案例,您可以更好地理解统计学知识点的概念和用途,并通过实际的Python代码示例和图形进行演示,帮助您在实际中应用这些知识。