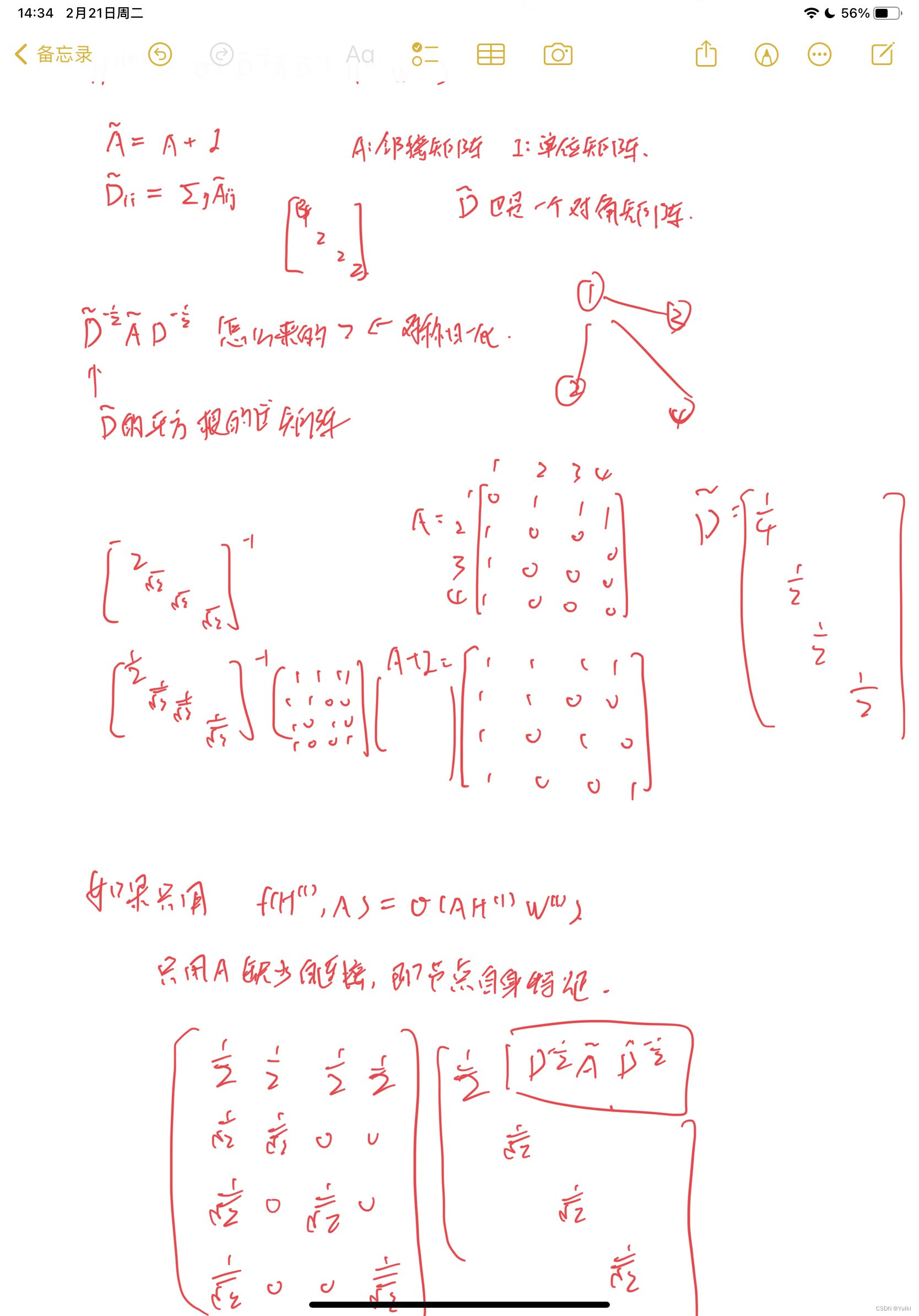
拉普拉斯矩阵(Laplacian Matrix)是一个与图相关的矩阵,通常用于图分析、机器学习和信号处理等领域。它是由图的邻接矩阵或关联矩阵计算得出的。
对于一个无向图 G = ( V , E ) G=(V,E) G=(V,E),它的拉普拉斯矩阵 L L L 可以表示为 L = D − A L=D-A L=D−A,其中 A A A 是图的邻接矩阵, D D D 是度数矩阵。度数矩阵 D D D 是一个对角矩阵,其中 D i i D_{ii} Dii 表示节点 i i i 的度数(即与节点 i i i 相连的边数),其余元素均为 0 0 0。邻接矩阵 A A A 则是一个对称矩阵,其中 A i j = 1 A_{ij}=1 Aij=1 表示节点 i i i 和节点 j j j 之间有一条边,否则 A i j = 0 A_{ij}=0 Aij=0。
对于一个有向图,有两种常用的拉普拉斯矩阵:对称归一化拉普拉斯矩阵和非对称拉普拉斯矩阵。对称归一化拉普拉斯矩阵定义为
L
=
D
−
1
/
2
(
D
−
A
)
D
−
1
/
2
L=D^{-1/2}(D-A)D^{-1/2}
L=D−1/2(D−A)D−1/2,其中
D
−
1
/
2
D^{-1/2}
D−1/2 是度数矩阵的平方根的逆矩阵。非对称拉普拉斯矩阵则是
L
=
D
−
A
L=D-A
L=D−A,其中
D
D
D 是度数矩阵。
对称归一化的拉普拉斯矩阵是通过将标准的拉普拉斯矩阵进行归一化得到的。在对称归一化的拉普拉斯矩阵中,每个非零节点都被除以该节点的度数的平方根,从而使得每个节点的度数对它的邻居节点的贡献相同。
下面是对称归一化的拉普拉斯矩阵的计算公式:
L s y m = D − 1 2 L D − 1 2 \mathbf{L}_{sym} = \mathbf{D}^{-\frac{1}{2}} \mathbf{L} \mathbf{D}^{-\frac{1}{2}} Lsym=D−21LD−21
其中, L \mathbf{L} L 是标准的拉普拉斯矩阵, D \mathbf{D} D 是度数矩阵, D i i D_{ii} Dii 表示第 i i i 个节点的度数。 D − 1 2 \mathbf{D}^{-\frac{1}{2}} D−21 表示度数矩阵的平方根的逆矩阵,即:
D − 1 2 = [ 1 D 1 0 ⋯ 0 0 1 D 2 ⋯ 0 ⋮ ⋮ ⋱ ⋮ 0 0 ⋯ 1 D n ] \mathbf{D}^{-\frac{1}{2}} = \begin{bmatrix} \frac{1}{\sqrt{D_{1}}} & 0 & \cdots & 0 \ 0 & \frac{1}{\sqrt{D_{2}}} & \cdots & 0 \ \vdots & \vdots & \ddots & \vdots \ 0 & 0 & \cdots & \frac{1}{\sqrt{D_{n}}} \end{bmatrix} D−21=[D110⋯0 0D21⋯0 ⋮⋮⋱⋮ 00⋯Dn1]
对称归一化的拉普拉斯矩阵的优点是能够避免不同节点度数差异较大造成的计算不平衡问题,从而提高了算法的稳定性和收敛速度。在图神经网络中,对称归一化的拉普拉斯矩阵也被广泛应用于图卷积神经网络(Graph Convolutional Network,GCN)等算法中。
最终可以实现近似的归一化,但是可以保证是一个对称矩阵
两个问题:
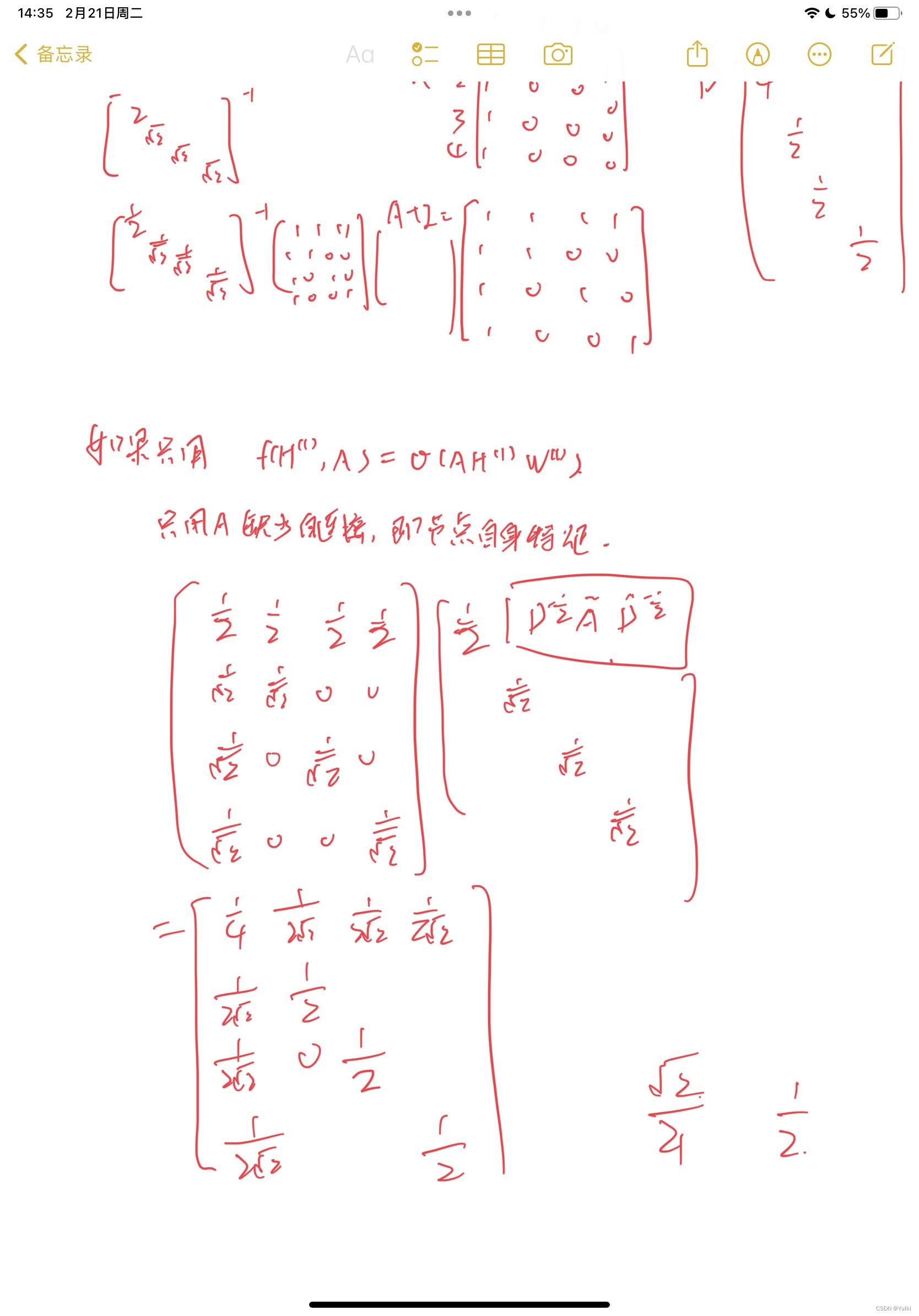
- 只使用A的话,由于A的对角线上都是0,所以在和特征矩阵H相乘的时候,只会计算一个node的所有邻居的特征的加权和,该node自己的特征却被忽略了。因此,我们可以做一个小小的改动,给A加上一个单位矩阵 I ,这样就让对角线元素变成1了。
- A是没有经过归一化的矩阵,这样与特征矩阵相乘会改变特征原本的分布,产生一些不可预测的问题。所以我们对A做一个标准化处理。首先让A的每一行加起来为1,我们可以乘以一个D的逆,D就是度矩阵。我们可以进一步把D的拆开与A相乘,得到一个对称且归一化的矩阵 :