PDF文档公众号回复关键字:20240619

2022 CSP-J 阅读程序2
阅读程序(判断题1.5分 选择题3分 共计40分 )
01 #include <algorithm>
02 #include <iostream>
03 #include <limits>
04
05 using namespace std;
06
07 const int MAXN = 105;
08 const int MAXK = 105;
09
10 int h[MAXN][MAXK];
11
12 int f(int n, int m)
13 {
14 if(m == 1) return n;
15 if(n == 0) return 0;
16
17 int ret = numeric_limits<int>::max();
18 for(int i=1; i<=n;i++)
19 ret = min(ret,max(f(n-i,m),f(i-1,m-1)+1));
20 return ret;
21 }
22
23 int g(int n,int m)
24 {
25 for(int i=1;i<=n;i++)
26 h[i][1]=i;
27 for(int j=1;j<=m;j++)
28 h[0][j]=0;
29
30 for(int i=1;i<=n;i++){
31 for(int j=2;j<=m;j++){
32 h[i][j]=numeric_limits<int>::max();
33 for(int k=1;k<=i;k++)
34 h[i][j]=min(
35 h[i][j],
36 max(h[i-k][j],h[k-1][j-1])+1);
37 }
38 }
39
40 return h[n][m];
41 }
42
43 int main()
44 {
45 int n,m;
46 cin>>n>>m;
47 cout<<f(n,m)<<endl<<g(n,m)<<endl;
48 return 0;
49 }
假设输入的n、m均时不超过100的正整数,完成下面的判断题和选择题
判断题
22.当输入为"7 3"时,第19行用来取最小值的min函数执行了449次( )
23.输出的两行整数总是相同的( )
24.当m为1时,输出的第一行总为n( )
单选题
25.算法g(n,m)最为准确的时间复杂度分析结果为( )
A. O( n 3 / 2 m n^{3/2}m n3/2m)
B. O(nm)
C. O( n 2 m n^2m n2m)
D. O( n m 2 nm^2 nm2)
26.当输入为"20 2"时,输出的第一行为( )
A. “4”
B. “5”
C. “6”
D. “20”
27.(4分)当输入为"100 100"时,输出的第一行为( )
A. “6”
B. “7”
C. “8”
D. “9”
2 相关知识点
1) 整数最大值
一般来说,数值类型的极值是一个与平台相关的特性。C++标准程序库通过template numeric_limits提供这些极值,取代传统C语言所采用的预处理常数
#include<bits/stdc++.h>
using namespace std;
/*
c++提供了一些求极值的函数
整数最大值 numeric_limits max min
*/
int main(){
int max_int = numeric_limits<int>::max();//int类型的最大值
cout<<max_int<<endl;//2147483647
int min_int = numeric_limits<int>::min();//int类型的最小值
cout<<min_int<<endl;//-2147483648
long long max_long = numeric_limits<long long>::max();//long long 类型的最大值
cout<<max_long<<endl;//9223372036854775807
return 0;
}
2) 递归(Recursion)
递归是一种解决问题的方法,它通过将问题分解为更小的子问题来解决。
一个递归函数会在其定义中直接或间接地调用自身
递归通常包括两个部分:基本情况(Base case)和递归步骤(Recursive step)。
基本情况是指当问题规模变得足够小时,可以直接得到解决方案的情况。
3) 递推(Recurrence)
递推是一种描述序列中项与项之间关系的方法。递推关系通常用于定义具有某种规律性的数列,如斐波那契数列
递推关系可以用一个公式或方程来表示,该公式或方程描述了序列中的每一项如何由前一项(或前几项)计算得出
4) 递归和递推区别
递归是一种解决问题的方法,通过将问题分解为更小的子问题来解决,自上而下分解,通常会出现多次重复计算问题
递推是一种描述序列中项与项之间关系的方法,自底而上计算,避免重复计算
通过斐波那契数列演示区别
递归f(3)重复计算3次,如果数更大重复更多
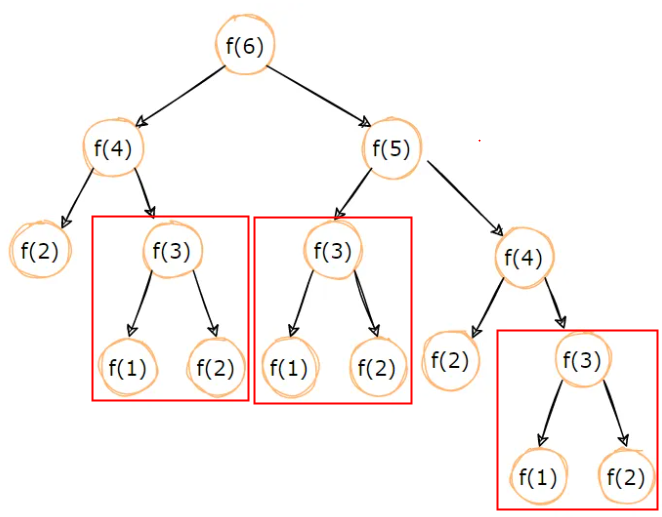
递推计算是从最底层计算,计算上一层时使用前面的计算结果,所以f(3)只计算1次
3 思路分析
假设输入的n、m均时不超过100的正整数,完成下面的判断题和选择题
判断题
22.当输入为"7 3"时,第19行用来取最小值的min函数执行了449次( )
答案 F
分析
19行min的计算次数有2步组成
1 for循环的次数,循环1次调用1次min函数
2 每次for循环包括2个递归调用,可以分别计算,由于递归调用出现多次重复计算,可以转换递推减少计算
令C(i,j)表示i行,j列时递归执行次数,计算如下表格,可以找到对应规律

23.输出的两行整数总是相同的( T )
分析
2行正数,对应2个函数的输出
从2个函数看,一个实现方式是递归,一个实现方式是动态规划,即递推记录到数组
初始值相同并且递归、递推式相同,所以在输入相同的情况下,输出结果相同
24.当m为1时,输出的第一行总为n( )
分析
//第1行输出,对应f函数
//从程序看m为1时 返回n 不进行递归调用,所以第1行总为n
if(m == 1) return n;
单选题
25.算法g(n,m)最为准确的时间复杂度分析结果为( C )
A. O( n 3 / 2 m n^{3/2}m n3/2m)
B. O(nm)
C. O( n 2 m n^2m n2m)
D. O( n m 2 nm^2 nm2)
分析
/*
算法g(n,m)的时间复杂度主要取决于如下代码
时间复杂度使用大O表示法
对于足够大的输入规模,我们往往不需要花费很大力气计算太精确的结果,通常指关系增长级量,即算法的渐进效率
所以for(int k=1;k<=i;k++) 中i和n不完全一致,但规模有相关性,因此通常使用n
所以如下3层嵌套循环时间复杂度O(n*m*n)
*/
30 for(int i=1;i<=n;i++){
31 for(int j=2;j<=m;j++){
32 h[i][j]=numeric_limits<int>::max();
33 for(int k=1;k<=i;k++)
34 h[i][j]=min(
35 h[i][j],
36 max(h[i-k][j],h[k-1][j-1])+1);
37 }
38 }
26.当输入为"20 2"时,输出的第一行为( C )
A. “4”
B. “5”
C. “6”
D. “20”
分析
第1行输出,对应f函数的返回值,由于f函数和g函数功能相同,g函数减少重复计算,所以我们可以g函数对应的值
g函数初始化了h[n][m]数组
m=1时,对应第1列初始值为n,分别1,2,3,4....
n=1时,第0行全是0
根据如下程序对应第2列赋值
h[1][1]=max(h[0][2],h[0][1])+1=1
h[2][2]=min(max(h[1][2],h[0][1])+1,max(h[0][2],h[1][1])+1)=min(1+1,1+1)=2
h[3][2]=min(max(h[2][2],h[0][1])+1,max(h[1][2],h[1][1])+1,max(h[0][2],h[2][1])+1)=min(2+1,1+1,2+1)=3
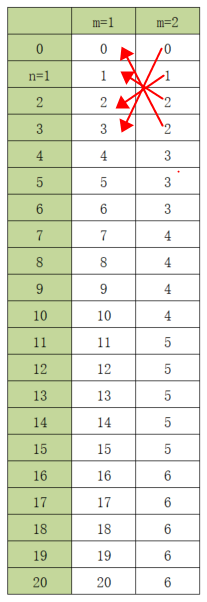
/*
2行2列时,如下图红色箭头四对,每一对取最大值+1
取4对中的最小值
*/
h[4][2]=min(max(h[3][2],h[0][1])+1,max(h[2][2],h[1][1])+1,max(h[1][2],h[2][1])+1,max(h[0][2],h[3][1])+1)=3
30 for(int i=1;i<=n;i++){
31 for(int j=2;j<=m;j++){
32 h[i][j]=numeric_limits<int>::max();
33 for(int k=1;k<=i;k++)
34 h[i][j]=min(
35 h[i][j],
36 max(h[i-k][j],h[k-1][j-1])+1);
37 }
38 }
/*
5行2列也是同样计算,结果为3
20行2列计算结果为6
*/
27.(4分)当输入为"100 100"时,输出的第一行为( B )
A. “6”
B. “7”
C. “8”
D. “9”
分析
入参非常大无论递归和动态规划表格计算都会有巨大的计算量
这个问题是测试鸡蛋硬度的问题,问题大概描述如下:
小明用2个玻璃瓶,在总高88层大楼测试瓶子硬度,拿1个从某层摔下去,瓶子没摔碎,到更高层去摔,如果碎了,拿另1瓶子到更低层摔
问测试出瓶子最大硬度最少摔几次?
上面程序通过递归和动态规划解决这个问题,主要是瓶子数量有限制,
在每一层,建设当前为k层都去试一下,如果碎了,少1个鸡蛋到更少的区间测试h[k-1][j-1]
如果没碎,到更高的高度去测试,测试的这些结果去最小值
此题如果瓶子足够的情况下,可以使用2分去测试,只要最多用7个鸡蛋就可以测试鸡蛋硬度最大可到第几层
2^7=128>100