图论算法基础
- 有向图
- 有向图的实现方式
- 无向图
- 无向图的实现方式
- 连通图
- 连通分量的定义
- 强连通图和强连通分量的定义
- 弱连通图和单向连通图的定义
- 判断图是否是强连通图,弱连通图还是单项连通图
- 一个很典型的错误代码
- JAVA实现
- C++实现
- 生成树
- 最小生成树
- 拓扑排序
- 邻接表的实现方式
- 数组模拟邻接表
- 容器模拟邻接表
- 拓扑排序面试题


有向图

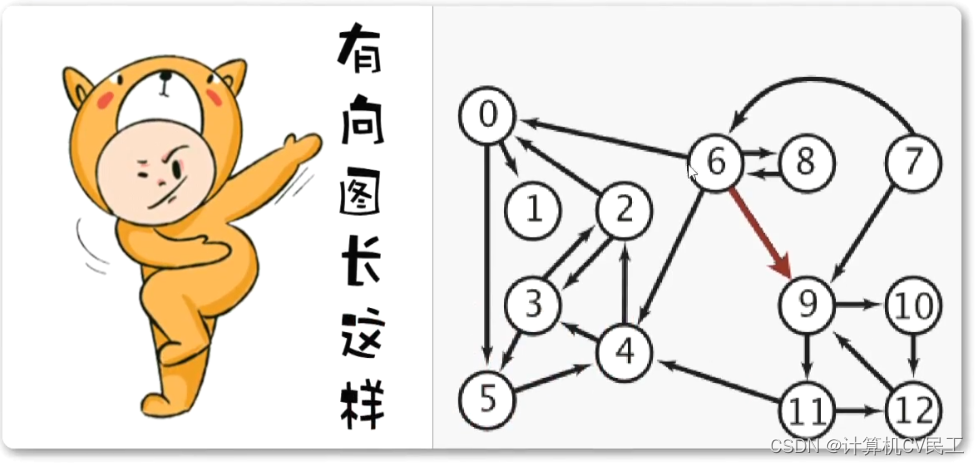
有向图的实现方式

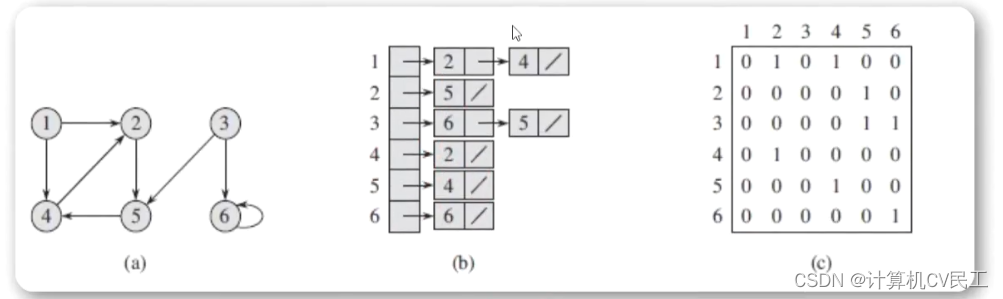
邻接表实现

一个例子

邻接矩阵

无向图
边没有方向的图称为无向图
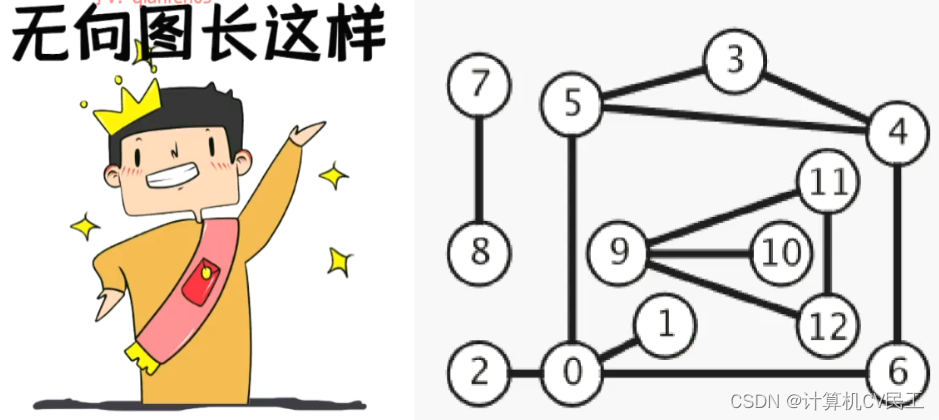
无向图的实现方式
用邻接表和邻接矩阵实现


一个例子(去掉所有的箭头)
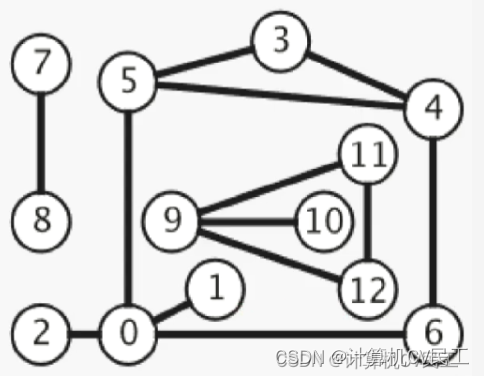
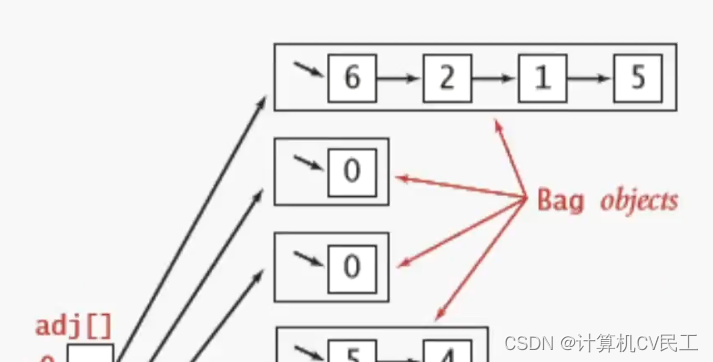


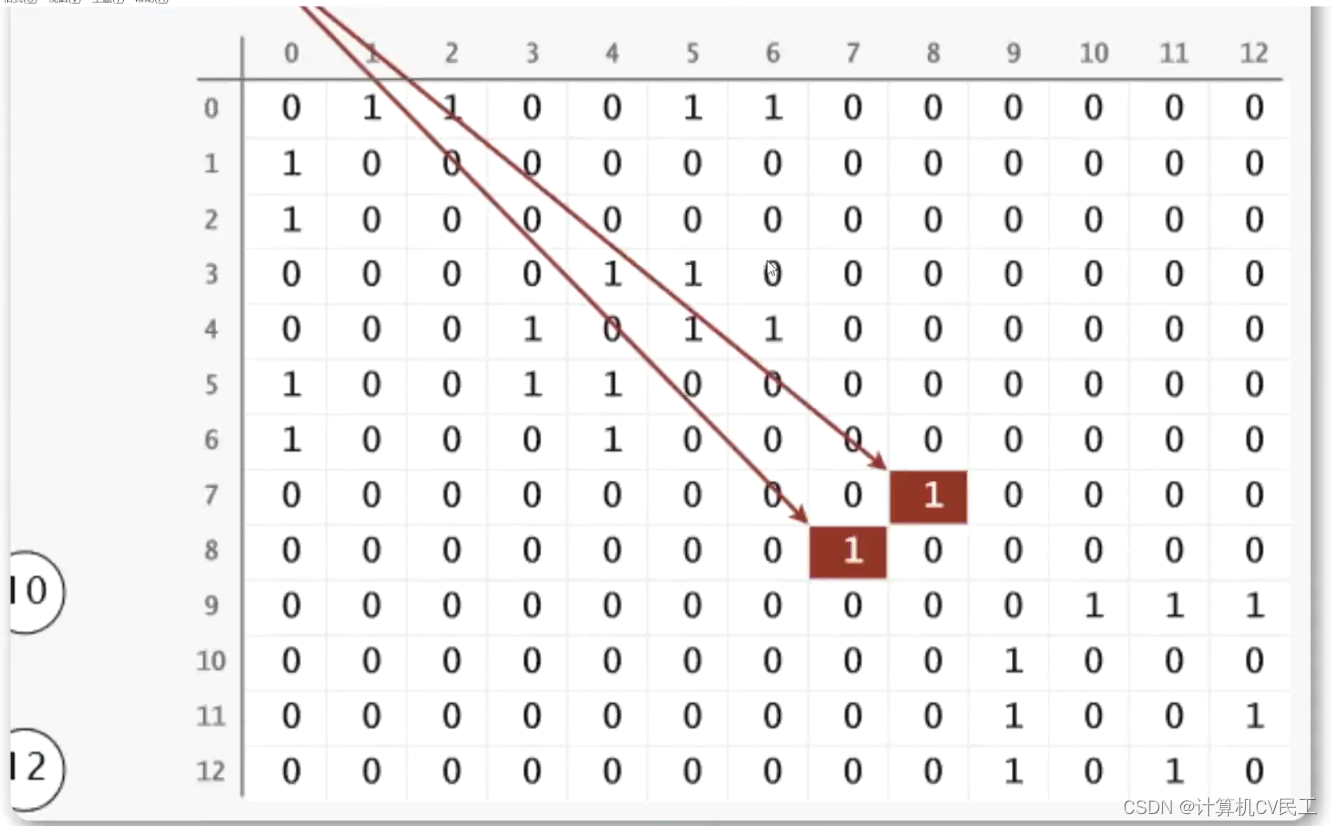
连通图


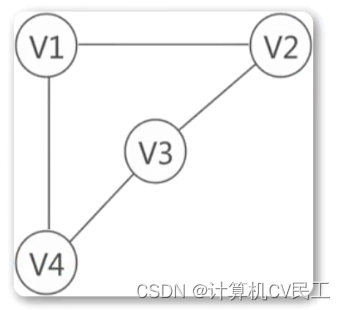

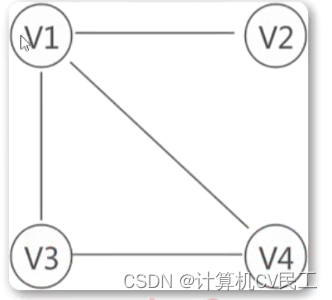
连通分量的定义

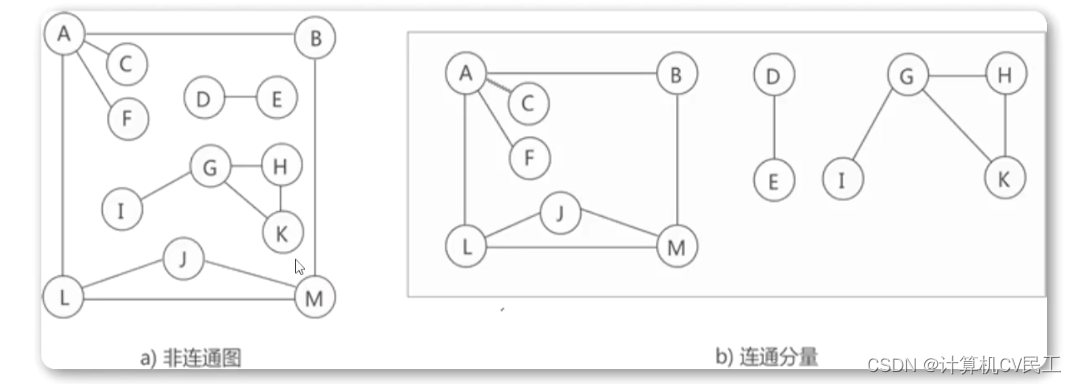
强连通图和强连通分量的定义

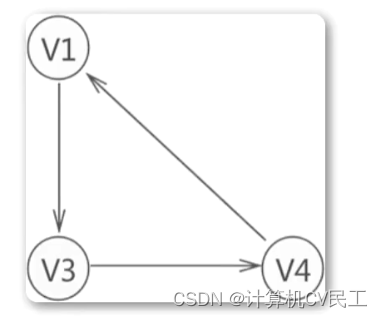

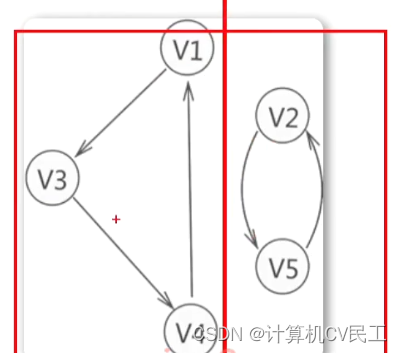
弱连通图和单向连通图的定义

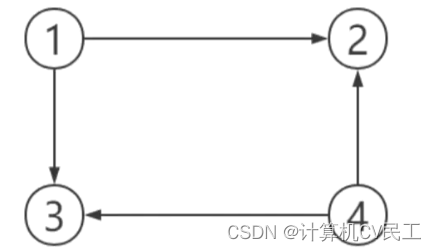
其中1不能到4,4也不能到1,所有此图只是弱连通图,不是单向连通图。
单向连通图

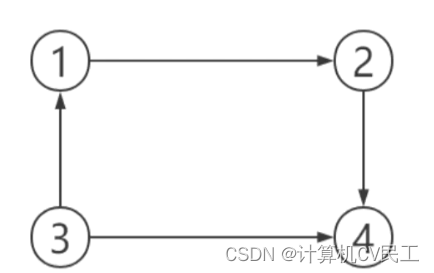
强连通图必是单向连通图,单向连通图必是弱连通图。(反正未必)
判断图是否是强连通图,弱连通图还是单项连通图

解题方法:先判断是否为弱连通图,然后单向连通图,最后判断是不是强连通图(从大范围到小范围的递进)
//
看一下有向图的邻接矩阵表示
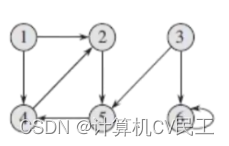
//强连通图
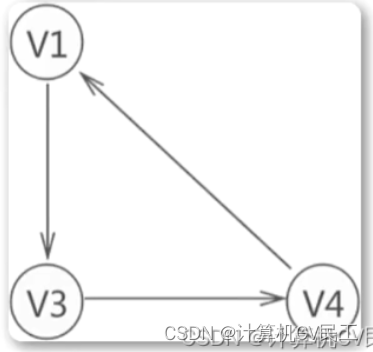
//单向连通图
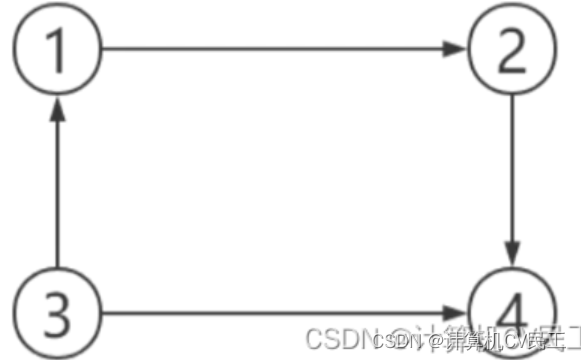
//弱连通图
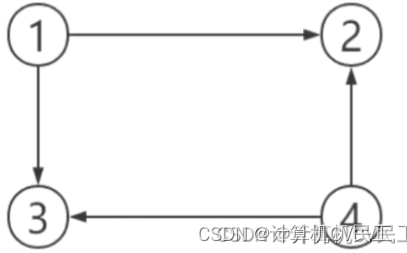
思路很简单,在邻接矩阵中,将间接连通的点连接起来,然后进行判断就行。
从大范围到小范围的缩小判断。。。先判断弱连通,再单向连通,再强连通
一个很典型的错误代码
package graphTheory;
import java.util.Scanner;
public class graphJudgeFalse {
public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
System.out.println("请输入节点数目");
int n = scanner.nextInt();
int a[][] =new int[n][n];
System.out.println("请输入邻接矩阵: ");
for (int i=0;i<n;i++){
for (int j =0;j<n;j++){
a[i][j] = scanner.nextInt();
}
}
// int[][] a = {{0,1,0,0},{0,0,0,1},{1,0,0,0},{0,0,1,0}};
// int n =4;
//将间接连通的节点连通(矩阵对应的位置值赋值为1)
for (int i=0;i<n;i++){
for (int k=0;k<n;k++){
for (int j=0;j<n;j++){
if(a[i][k]!=0&&a[k][j]!=0){
a[i][j]=1;
}
}
}
}
//判断图类型
for (int i=0;i<n;i++){
for (int j=0;j<n;j++){
if(i!=j&&a[i][j]==0&&a[j][i]==0){
//存在互不连通的点
System.out.println("该图为弱连通图");
return;
}
}
}
for (int i=0;i<n;i++){
for (int j=0;j<n;j++){
if(i!=j&&a[i][j]+a[j][i]==1){
//存在只通单边的点(单向点)
System.out.println("该图为单向通图");
return;
}
}
}
//到这里,说明所有的点都可以双向到达
System.out.println("该图为强连通图");
}
}
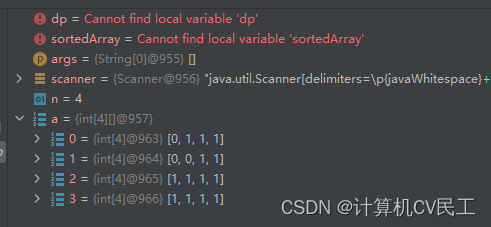
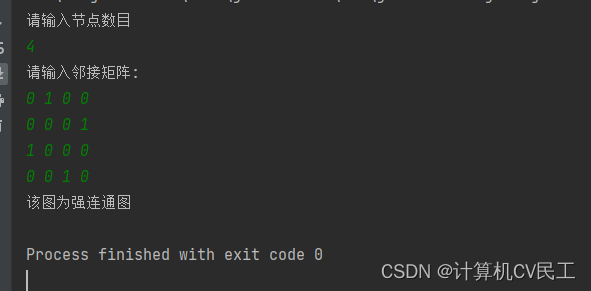
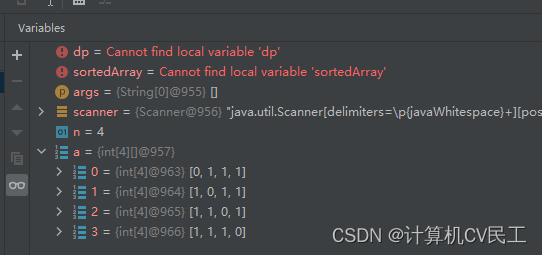
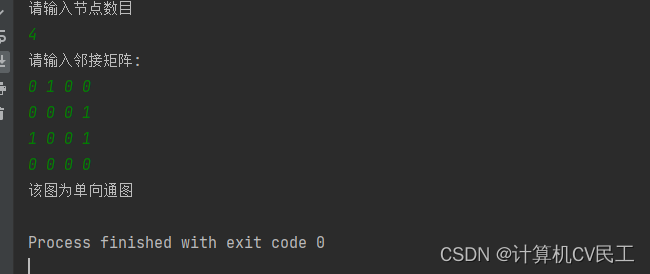
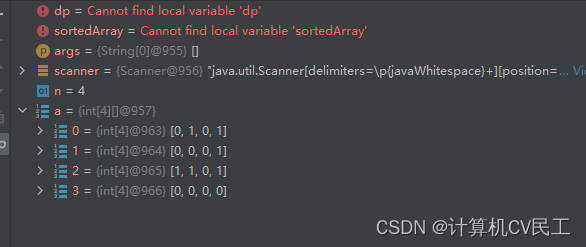
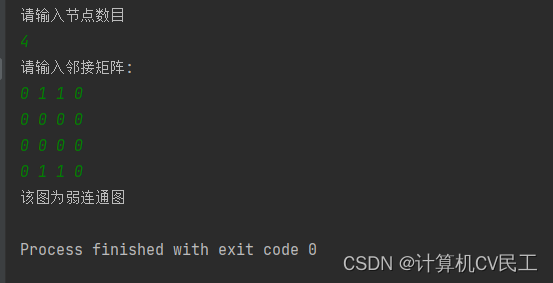
输入强连通图的邻接矩阵,得到错误的结果


原因: 2节点到1节点是连通的,
但是循环赋值的时候a[2][4]!=0 而a[4][ j ]中只有a[4][3]为1所以a[2][3]==1(2和3连通)
就略过了2和1的连通,到了a[3][…]了,导致误判为单向连通图,
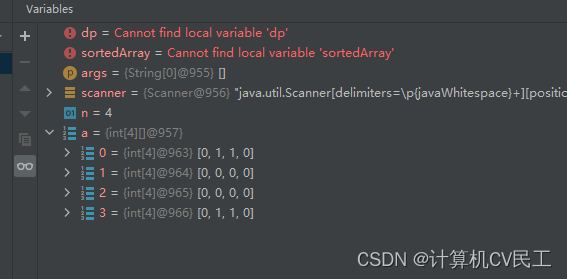
并且a[i][j]中i和j相同值的位置也错误的赋值为1
(注意:这里没考虑数组下标为0开始,默认a[1][1]就是对应1,1位置,
实际代码是从0到3)
JAVA实现
package graphTheory;
import java.util.Scanner;
public class graphJudge {
public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
System.out.println("请输入节点数目");
int n = scanner.nextInt();
int a[][] =new int[n][n];
System.out.println("请输入邻接矩阵: ");
for (int i=0;i<n;i++){
for (int j =0;j<n;j++){
a[i][j] = scanner.nextInt();
}
}
// int[][] a = {{0,1,0,0},{0,0,0,1},{1,0,0,0},{0,0,1,0}};
// int n =4;
//将间接连通的节点连通(矩阵对应的位置值赋值为1)
for (int i=0;i<n;i++){
for (int k=0;k<n;k++){
for (int j=0;j<n;j++){
if(a[i][k]!=0&&a[k][j]!=0&&(i!=j)){
a[i][j]=1;
}
}
}
}
//第二次循环赋值是为了吧第一次漏掉的点补上来。。。。
for (int i=0;i<n;i++){
for (int k=0;k<n;k++){
for (int j=0;j<n;j++){
if(a[i][k]!=0&&a[k][j]!=0&&(i!=j)){
a[i][j]=1;
}
}
}
}
//判断图类型
for (int i=0;i<n;i++){
for (int j=0;j<n;j++){
if(i!=j&&a[i][j]==0&&a[j][i]==0){
//存在互不连通的点
System.out.println("该图为弱连通图");
return;
}
}
}
for (int i=0;i<n;i++){
for (int j=0;j<n;j++){
if(i!=j&&a[i][j]+a[j][i]==1){
//存在只通单边的点(单向点)
System.out.println("该图为单向通图");
return;
}
}
}
//到这里,说明所有的点都可以双向到达
System.out.println("该图为强连通图");
}
}
C++实现
#include <iostream>
using namespace std;
int main()
{
system("chcp 65001");
int n;
cout<<"输入节点个数";
cin>>n;
cout<<"输入邻接矩阵";
int** a = (int**)malloc(sizeof(int*)*n);
for(int i=0;i<n;i++)
{
a[i]=(int*)malloc(sizeof(int)*n);
}
for(int i = 0;i<n;i++){
for (int j = 0; j < n; j++)
{
cin>>a[i][j];
}
}
//将间接连接的点连接
for(int i = 0;i<n;i++){
for(int k=0;k<n;k++){
for(int j=0;j<n;j++){
if(a[i][k]!=0&&a[k][j]!=0&&(i!=j)){
a[i][j]=1;
}
}
}
}
//第二次循环补漏
for(int i = 0;i<n;i++){
for(int k=0;k<n;k++){
for(int j=0;j<n;j++){
if(a[i][k]!=0&&a[k][j]!=0&&(i!=j)){
a[i][j]=1;
}
}
}
}
//判断类型
for (int i=0;i<n;i++){
for (int j=0;j<n;j++){
if(i!=j&&a[i][j]==0&&a[j][i]==0){
//存在互不连通的点
std:cout<<"该图为弱连通图";
return 0;
}
}
}
for (int i=0;i<n;i++){
for (int j=0;j<n;j++){
if(i!=j&&a[i][j]+a[j][i]==1){
//存在只通单边的点(单向点)
cout<<"该图为单向通图";
return 0;
}
}
}
//到这里,说明所有的点都可以双向到达
cout<<"该图为强连通图";
return 0;
}

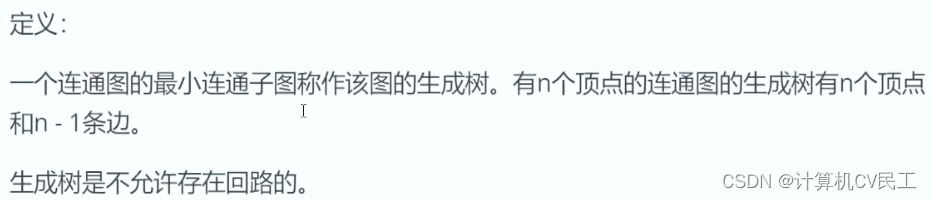
生成树
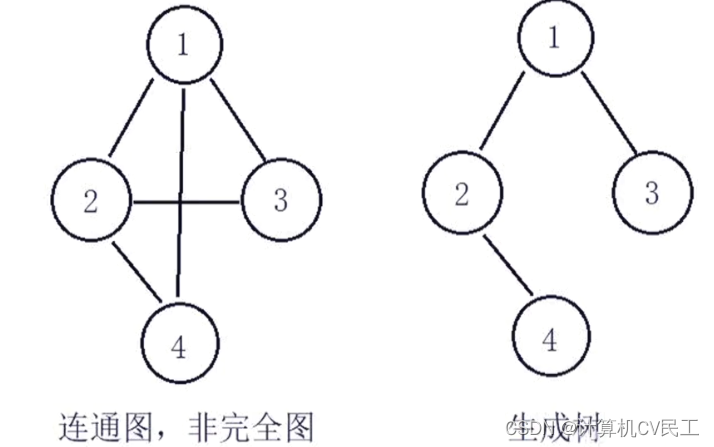
最小生成树

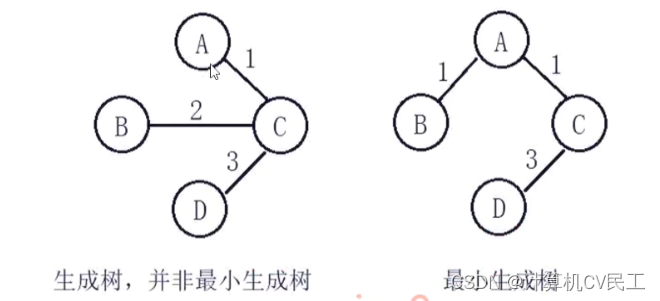
稀疏图用邻接表存储,稠密图用邻接矩阵存储
拓扑排序


拓扑序列一定是针对有向图的
拓扑排序无环
能够拓扑排序的图是:有向无环图
有向图的拓扑排序就是宽度优先搜索的应用
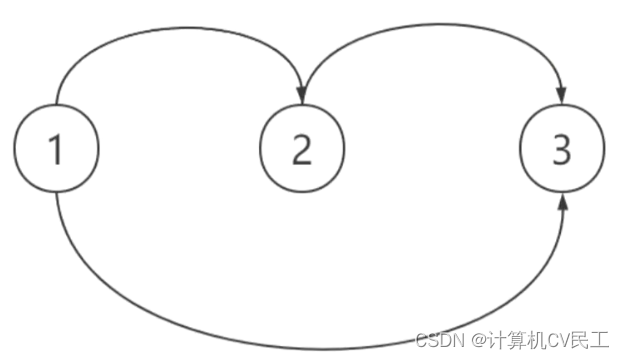


如果存在环的话,一定会存在一些点不会入队。因为有的边删不了,所以不可以进行拓扑排序