一、 问题描述

二、算法思想

这是一个背包问题,可以使用动态规划算法来解决。具体思路如下:
- 定义一个二维数组dp,dp[i][j]表示前i个物品在背包容量为j时能获取的最大价值。
- 初始化dp数组的第一行和第一列为0,表示当只有一个物品或背包容量为0时,最大价值为0。
- 遍历每个物品i和每个背包容量j,根据以下状态转移方程更新dp数组:
- 如果物品i的重量大于背包容量j,则无法放入背包,dp[i][j] = dp[i-1][j]。
- 如果物品i的重量小于等于背包容量j,则考虑放入或不放入物品i的情况:
- 放入物品i,dp[i][j] = dp[i-1][j-weight[i]] + value[i],其中weight[i]表示物品i的重量,value[i]表示物品i的价值。
- 不放入物品i,dp[i][j] = dp[i-1][j]。
- 选择较大的值作为dp[i][j]。
- 从dp数组的最后一个元素往前遍历,根据状态转移方程可以得到装入背包的物品编号。
- 输出装入背包的物品编号。
三、代码实现
#include <stdio.h>
#define MAX_ITEMS 100
#define MAX_WEIGHT 1000
int max(int a, int b) {
return (a > b) ? a : b;
}
// 动态规划求解背包问题
void knapsack(int n, int capacity, int weights[], int values[]) {
int dp[MAX_ITEMS + 1][MAX_WEIGHT + 1] = {0};
int i, w;
// 填表格
for (i = 1; i <= n; i++) {
for (w = 1; w <= capacity; w++) {
if (weights[i - 1] > w) {
dp[i][w] = dp[i - 1][w];
} else {
dp[i][w] = max(dp[i - 1][w], values[i - 1] + dp[i - 1][w - weights[i - 1]]);
}
}
}
// 回溯找出装入背包的物品
int res[MAX_ITEMS];
int k = n, c = capacity;
int num = 0;
while (k > 0 && c > 0) {
if (dp[k][c] != dp[k - 1][c]) {
res[num++] = k;
c -= weights[k - 1];
}
k--;
}
// 输出结果
for (i = num - 1; i >= 0; i--) {
printf("%-d ", res[i]);
}
printf("\n");
printf("end");
}
int main() {
int n, capacity;
scanf("%d %d", &n, &capacity);
int weights[MAX_ITEMS], values[MAX_ITEMS];
for (int i = 0; i < n; i++) {
scanf("%d", &weights[i]);
}
for (int i = 0; i < n; i++) {
scanf("%d", &values[i]);
}
// 调用背包问题求解函数
knapsack(n, capacity, weights, values);
return 0;
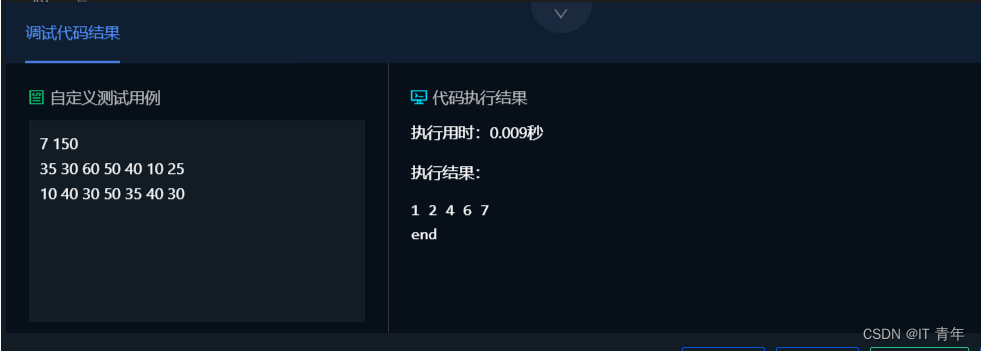
}执行结果
 结语
结语
如果你喜欢一匹马
不必去追,去种草
来年会有一群马向你奔来
!!!