线性DP
例题1
1143. 最长公共子序列 (LCS)
子序列不连续
给定两个字符串 text1 和 text2,返回这两个字符串的最长 公共子序列 的长度。如果不存在 公共子序列 ,返回 0 。
一个字符串的 子序列 是指这样一个新的字符串:它是由原字符串在不改变字符的相对顺序的情况下删除某些字符(也可以不删除任何字符)后组成的新字符串。
- 例如,
"ace"是"abcde"的子序列,但"aec"不是"abcde"的子序列。
两个字符串的 公共子序列 是这两个字符串所共同拥有的子序列。
示例 1:
输入:text1 = "abcde", text2 = "ace" 输出:3 解释:最长公共子序列是 "ace" ,它的长度为 3 。
本质是选或不选
dfs(i,j)表示s的前i个字母和t的前j个字母的LCS长度
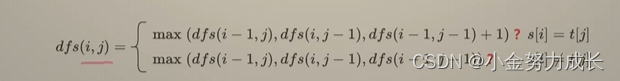
当s[i]=t[j]的时候,dfs(i-1,j-1)+1是要大于前面两个的,舍弃前两个
s[i]!=t[j]的时候,前面两个会自动递归到 dfs(i-1,j-1)+1,因此舍弃
代码:
class Solution:
def longestCommonSubsequence(self, text1: str, text2: str) -> int:
x=len(text1)
y=len(text2)
@cache
def dfs(n,m):
if n<0 or m<0:
return 0
if text1[n]==text2[m]:
return (dfs(n-1,m-1)+1)
if text1[n]!=text2[m]:
return max(dfs(n-1,m),dfs(n,m-1))
return dfs(x-1,y-1)
改成数组:注意避免负数下标,这里都往后移一位
class Solution:
def longestCommonSubsequence(self, text1: str, text2: str) -> int:
x1=len(text1)
y1=len(text2)
f=[[0]*(y1+1) for _ in range(x1+1)]
for i,x in enumerate(text1):
for j,y in enumerate(text2):
if x==y:
f[i+1][j+1]=f[i][j]+1
else:
f[i+1][j+1]=max(f[i][j+1],f[i+1][j])
return f[x1][y1]
72. 编辑距离
给你两个单词 word1 和 word2, 请返回将 word1 转换成 word2 所使用的最少操作数 。
你可以对一个单词进行如下三种操作:
- 插入一个字符
- 删除一个字符
- 替换一个字符
示例 1:
输入:word1 = "horse", word2 = "ros" 输出:3 解释: horse -> rorse (将 'h' 替换为 'r') rorse -> rose (删除 'r') rose -> ros (删除 'e')
思路:从末尾值开始比较,如果s[i]=t[j] 直接dfs(i-1.j-1),因为不能改变这个值已经想同了
删除一个字母:相当于去掉s[i],也就是dfs(i,j-1)
插入一个字母,插入的肯定是和t[j]是一样的,所以是dfs[i+1,j],因为此时s[i]=t[j] ,所以同时减去1,得到最终答案dfs(i.j-1)
替换:把s【i】替换成t【j】,在同时减去1,也就是dfs(i-1,j-1)+1
代码:
class Solution:
def minDistance(self, word1: str, word2: str) -> int:
n=len(word1)
m=len(word2)
@cache
def dfs(i,j):
if i<0:
return j+1
if j<0:
return i+1
if word1[i]==word2[j]:
return dfs(i-1,j-1)
return min(dfs(i-1,j),dfs(i,j-1),dfs(i-1,j-1))+1
return dfs(n-1,m-1)数组:
class Solution:
def minDistance(self, s: str, t: str) -> int:
n, m = len(s), len(t)
f = [[0] * (m + 1) for _ in range(n + 1)]
f[0] = list(range(m + 1))
for i, x in enumerate(s):
f[i + 1][0] = i + 1
for j, y in enumerate(t):
f[i + 1][j + 1] = f[i][j] if x == y else \
min(f[i][j + 1], f[i + 1][j], f[i][j]) + 1
return f[n][m]
#f[0] = list(range(m + 1))表示初始化第一行,即s为空字符串时与t的编辑距离。因为此时s为空,所以只需要插入操作即可将t转换为s,所以第一行从0开始递增。
f[i + 1][0] = i + 1表示初始化第一列,即t为空字符串时与s的编辑距离。因为此时t为空,所以只需要删除操作即可将s转换为t,所以第一列从0开始递增。300. 最长递增子序列
给你一个整数数组 nums ,找到其中最长严格递增子序列的长度。
子序列 是由数组派生而来的序列,删除(或不删除)数组中的元素而不改变其余元素的顺序。例如,[3,6,2,7] 是数组 [0,3,1,6,2,2,7] 的
子序列
。
示例 1:
输入:nums = [10,9,2,5,3,7,101,18] 输出:4 解释:最长递增子序列是 [2,3,7,101],因此长度为 4 。
递归代码:
class Solution:
def lengthOfLIS(self, nums: List[int]) -> int:
n=len(nums)
@cache
def dfs(i):
res=0
for x in range(i):
if nums[x]<nums[i]:
res= max(res,dfs(x))
return res+1
ans=0
return max(dfs(i) for i in range(n))转化成数组
class Solution:
def lengthOfLIS(self, nums: List[int]) -> int:
n=len(nums)
f=[0]*n
for i in range(n):
for j in range(i):
if nums[j]<nums[i]:
f[i]=max(f[j],f[i])
f[i]+=1
return max(f)