文章目录
- 什么是图
- 图的分类
- 图算法的复杂度
- 图的模拟
- 怎么储存一个图
- 邻接矩阵:
- 邻接矩阵的定义方式
- 优劣分析
- 邻接表
- 优劣分析
- 实现代码
- 链式前向星
- 实现代码
- 优劣分析
- 图的遍历
- 某个点的连通性
- 拓扑排序
- 1.拓扑排序的概念
- 2.图的入度和出度
- 3.基于 B F S BFS BFS的拓扑排序
- 复杂度分析
- 4.基于 D F S DFS DFS搜索的拓扑排序
- 细节处理
什么是图
图是常见的抽象模型,由点和连接点的边(edge)组成。图是点和边构成的网。图描述了事物之间的连接。图最典型的应用场景是地图,地图由地点和道路组成,它的特征如下。
- 地点:可能是十字路口,也可能是三岔路口,或者仅仅是一个连接点。在图论中,把地点抽象为点。
- 道路:可能是单行道或双行道。抽象成有向边或无向边。
- 道路有过路费:抽象成边的权值。
- 求两点间的最短道路,即图论里的最短路径算法。
- 在城市群之间如何修最短的连通道路,即图论中的最小生成树问题。地图的这些问题都是图论研究的对象。计算机网络也是典型的图问题,和地图非常相似。
树是一种特殊的图。树的结点从根开始,层层扩展子树,是一种层次关系,这种层次关系保证了树上的结点不会出现环路。在图的算法中,经常需要在图上生成一棵树,再进行操作。
图的分类
根据边有无方向、有无权值、有无环路,可以把图分成很多种,例如:
- 无向无权图:边没有权值、没有方向;
- 有向无权图:边有方向、无权值;
- 加权无向图:边有权值,但没有方向;
- 加权有向图:边有权值,也有方向
- 有向无环图 ( D A G ) (DAG) (DAG)。
图算法的复杂度
图算法的复杂度显然和边的数量 E E E、点的数量 V V V相关。如果一个算法的复杂度是线性时间 O ( V + E ) O(V+E) O(V+E),这几乎是图问题中能达到的最好程度了。如果能达到 O ( V l o g 2 E ) O_{(Vlog₂E)} O(Vlog2E)、 O ( E l o g 2 V ) O(Elog₂V) O(Elog2V)或类似的复杂度,则是很好的算法。如果是 O ( V 2 ) O(V²) O(V2)、 O ( E 2 ) O(E²) O(E2)或更高,在图问题中不算是好的算法。
图的模拟
怎么储存一个图
对图的任何操作都需要基于一个存储好的图。图的存储结构必须是一种有序的存储,能让程序很快定位结点
u
u
u 和
v
v
v 的边
(
u
,
v
)
(u,v)
(u,v),最好能在
O
(
1
)
O(1)
O(1)的时间内只用一次或几次就定位到。
一般用3种数据结构存储图:
- 即邻接矩阵
- 邻接表
- 链式前向星
以如下的有向图为例
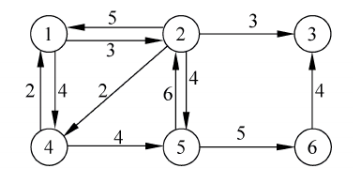
邻接矩阵:
邻接矩阵的定义方式
用二维数组存储即可:
i
n
t
g
r
a
p
h
[
N
]
[
N
]
int\ graph[N][N]
int graph[N][N],每个节点
g
r
a
p
h
[
i
]
[
j
]
graph[i][j]
graph[i][j] 表示从
i
i
i 到
j
j
j 的距离。
对于无向图有:
g
r
a
p
h
[
i
]
[
j
]
=
g
r
a
p
h
[
j
]
[
i
]
graph[i][j]=graph[j][i]
graph[i][j]=graph[j][i]。
对于有向图有:
g
r
a
p
h
[
i
]
[
i
]
!
=
g
r
a
p
h
[
j
]
[
i
]
graph[i][i]!=graph[j][i]
graph[i][i]!=graph[j][i]。
权值:如图则有:
g
r
a
p
h
[
1
]
[
2
]
=
3
、
g
r
a
p
h
[
2
]
[
1
]
=
5
…
…
graph[1][2]=3、graph[2][1]=5……
graph[1][2]=3、graph[2][1]=5……;用
g
r
a
p
h
[
i
]
[
j
]
=
+
∞
graph[i][j]=+\infty
graph[i][j]=+∞表示
i
i
i 和
j
j
j 之间无边。
优劣分析
优点:
- 编码非常简短。
- 适用于稠密图。
- 对边的存储、查询、更新等操作又快又简单,只需要一步就能访问和修改。
缺点: - 存储复杂度 O ( V 2 ) O(V²) O(V2)太高。如果用来存稀疏图,大量空间会被浪费。例如上面的图, 6 6 6个点,只有 11 11 11条边,但是 g r a p h [ 6 ] [ 6 ] graph[6][6] graph[6][6]的空间是 36 36 36。当 V = 10000 V=10000 V=10000个结点时,空间为 100 M B 100MB 100MB,已经超过了常见竞赛题的空间限制,而一百万个点的图在竞赛题中是很常见的。
- 一般情况下不能存储重边。 ( u , v ) (u,v) (u,v) 之间可能有两条或更多的边,这些边的费用不同、容量不同,是不能合并的。有向边 ( u , v ) (u,v) (u,v)在矩阵中只能存储一个参数,矩阵本身的局限性使它不能存储重边。
邻接表
邻接表是一种常用的图的存储方式,它可以用链表表示图的结构。在邻接表中,每个节点都对应一个链表,链表中存储了与该节点相连的所有节点。规模大的稀疏图一般用邻接表存储。
优劣分析
有点:
- 存储效率非常高,只需要与边数成正比的空间,存储复杂度为 O ( V + E ) O(V+E) O(V+E)。
- 能存储重边。
缺点: - 编程比邻接矩阵麻烦。
- 访问和修改效率稍低稍慢。
实现代码
vector<int>G[N]; //邻接表
void init(){ //初始化
for(int i = 0; i < N; i++)
G[i].clear();
}
void addEdge(int x, int y){ //插入路径:x -> y
G[x].push_back(y);
}
对于上图所成的邻接表如下:
| i = 1 i=1 i=1 | 2 | 4 | ||
|---|---|---|---|---|
| i = 2 i=2 i=2 | 1 | 3 | 4 | 5 |
| i = 3 i=3 i=3 | n u l l null null | |||
| i = 4 i=4 i=4 | 1 | 5 | ||
| i = 5 i=5 i=5 | 2 | 6 | ||
| i = 6 i=6 i=6 | 3 |
链式前向星
用邻接表存图非常节省空间,一般的大图也够用了。那如果空间极其紧张,有没有更紧凑的存图方法呢?邻接表有没有改进的空间?
分析邻接表的组成:存储一个结点
u
u
u 的邻接边,其方法的关键是先定位第
1
1
1个边,第
1
1
1个边再指向第
2
2
2个边,第
2
2
2个边再指向第
3
3
3个边……根据这个分析,可以设计一种极为紧凑、没有任何空间浪费、编码非常简单的存图方法。下图是对前面的图生成的存储空间,其中,
h
e
a
d
[
N
U
M
]
head[NUM]
head[NUM]是一个静态数组,
s
t
r
u
c
t
e
d
g
e
struct\ edge
struct edge是一个结构的静态数组,至少包含
t
o
和
n
e
x
t
to和next
to和next 两项元素。

以结点
2
2
2为例:
从点
2
2
2出发的边有
4
4
4条,即
(
2
,
1
)
(2,1)
(2,1)、
(
2
,
3
)
(2,3)
(2,3)、
(
2
,
4
)
(2,4)
(2,4)、
(
2
,
5
)
(2,5)
(2,5),邻居是
1
、
3
、
4
、
5
1、3、4、5
1、3、4、5。
- 定位第 1 1 1个边。用 h e a d [ ] head[\ ] head[ ]数组实现,例如 h e a d [ 2 ] head[2] head[2]指向结点 2 2 2的第 1 1 1个边, h e a d [ 2 ] = 8 head[2]=8 head[2]=8,它存储在 e d g e [ 8 ] edge[8] edge[8]这个位置。
- 定位其他边。用 e d g e edge edge的 n e x t next next参数指向下一个边。 e d g e [ 8 ] . n e x t = 6 edge[8].next=6 edge[8].next=6,下一个边在 e d g e [ 6 ] edge[6] edge[6]这个位置,然后 e d g e [ 6 ] . n e x t = 4 edge[6].next=4 edge[6].next=4, e d g e [ 4 ] . n e x t = 1 edge[4].next=1 edge[4].next=1,最后 e d g e [ 1 ] . n e x t = — 1 edge[1].next=—1 edge[1].next=—1,-1表示结束。
s
t
r
u
c
t
e
d
g
e
struct\ edge
struct edge的
t
o
to
to参数记录这个边的邻居结点。例如
e
d
g
e
[
8
]
.
t
o
=
5
edge[8].to=5
edge[8].to=5,第一个邻居是点
5
5
5;然后
e
d
g
e
[
6
]
.
t
o
=
4
edge[6].to=4
edge[6].to=4,
e
d
g
e
[
4
]
.
t
o
=
3
edge[4].to=3
edge[4].to=3,
e
d
g
e
[
1
]
.
t
o
=
1
edge[1].to=1
edge[1].to=1,得到邻居是
1
、
3
、
4
、
5
1、3、4、5
1、3、4、5。
上述存储方法被称为“链式前向星”,它是空间效率最高的存储方法,因为它用静态数组模拟邻接表,没有任何浪费。
实现代码
const long long N = 1e7 + 6; //百万节点百万边
struct Edge{
int next, to, w; //终点to,下一条边next,权值w
};
Edge edge[N];
int head[N]; //head[i]表示指向i节点的第一条边的位置
int cnt = 0; //cnt记录的是edge的末尾,新加入的位置都在末尾
void init(){
cnt = 0;
for(int i = 0; i < N; i++){
edge[i].next = -1;
head[i] = -1;
}
}
void addEdge(int u, int v, int w){
//添加u到v边,权值为w
edge[cnt].to = v;
edge[cnt].w = w;
edge[cnt].next = head[u];
head[u] = cnt;
cnt++;
}
for(int i = head[u]; i != -1; i = edge[i].next){
//遍历i的所有邻居
}
优劣分析
优点:
- 存储效率高
- 程序简单
- 能存储重边
缺点: - 不方便做删除操作。可尝试自己编写删除的程序
图的遍历
图的遍历与之前提过的树遍历类似。但是用DFS(递归)来搜索图,比BFS更难理解,但是一旦理解之后,编程将十分便利。图论中的很多算法,例如拓扑排序、强连通分量等,都建立在DFS之上。
下面是DFS的示例程序,其中用vector邻接表来存图。
vector<int>G[N]; //G[i][j]表示点i和点j之间的距离
int vis[N]; //vis = 0 表示这个点没有被访问过
//vis = 1 表示访问过了
//vis = -1 表示正在被访问中(拓扑排序跳出死循环可用)
bool dfs(int u){
vis[u] = 1;
if(……){……;return true;} //出现目标,返回正确
if(……){……;return false;} //处理并返回错误
for(int i = 0; i < G[u].size(); i++){//u的邻居有G[u].size个
int v = G[u][i]; //v是第i个邻居
if(!vis[v]){ //没有访问过就从这里继续
return dfs(v);
}
}
{……………………} //后续处理
}
某个点的连通性
对需要的点执行
d
f
s
dfs
dfs,就能找到它连通的点。例如找图中
e
e
e 点的连通性,执行
d
f
s
(
e
)
dfs(e)
dfs(e),访问过程见图结点上面的数字,顺序是
e
→
b
→
d
→
c
→
a
e\rightarrow b\rightarrow d\rightarrow c\rightarrow a
e→b→d→c→a。递归返回的结果见结点下面画线的数字,顺序是
a
→
c
→
d
→
b
→
e
a\rightarrow c\rightarrow d\rightarrow b\rightarrow e
a→c→d→b→e。虚线指向的结点表示不再访问,因为前面已经被访问过。

上面DFS的结果生成了一棵树,称为深搜优先生成树(
d
e
p
t
h
−
f
i
r
s
t
s
p
a
n
n
i
n
g
t
r
e
e
depth-firstspanning\ tree
depth−firstspanning tree),有以下概念:
- 树边:树上的边称为树边 ( t r e e e d g e ) (tree\ edge) (tree edge)。
- 回退边:虚线表示的边 ( a , b ) (a,b) (a,b)称为回退边 ( b a c k e d g e ) (back\ edge) (back edge),它不在树上。
- 在这棵树上,从起点到其他任何一个点只有一条路径。如果是无向图生成的树,那么任意两个点之间只有一条路径。
拓扑排序
图的
B
F
S
BFS
BFS和
D
F
S
DFS
DFS的一个直接应用是拓扑排序。
在现实生活中,人们经常要做一连串事情,这些事情之间有顺序关系或者有依赖关系,在做一件事情之前必须先做另一件事,比如安排客人的座位、穿衣服的先后、课程学习的先后等。这些事情都可以抽象为图论中的拓扑排序。
1.拓扑排序的概念
设有
a
、
b
、
c
、
d
a、b、c、d
a、b、c、d等事情,其中
a
a
a 有最高优先级,
b
、
c
b、c
b、c 优先级相同,
d
d
d 是最低优先级,表示为
a
→
(
b
,
c
)
→
d
a→(b,c)→d
a→(b,c)→d,那么
a
b
c
d
abcd
abcd 或
a
c
b
d
acbd
acbd 都是可行的排序。把事情看成图的点,把先后关系看成有向边,问题转化为在图中求一个有先后关系的排序,这就是拓扑排序。如下图左所示。
显然,一个图能进行拓扑排序的充要条件是它是一个有向无环图(
D
A
G
DAG
DAG)。有环图不能进行拓扑排序。

2.图的入度和出度
拓扑排序需要用到点的入度和出度的概念。
- 出度:以点 u u u 为起点的边的数量称为 u u u 的出度。
- 入度:以点
v
v
v 为终点的边的数量称为
v
v
v 的入度。
一个点的入度和出度体现了这个点的先后关系:如果一个点的入度等于 0 0 0,则说明它是起点,是排在最前面的;如果它的出度等于 0 0 0,则说明它是排在最后面的。例如在上图右中,点 a 、 c a、c a、c的入度为 0 0 0,它们都是优先级最高的事情; d d d 的出度为 0 0 0,它的优先级最低。
拓扑排序可以有多个,例如上图右中的a和c,谁排在前面都可以: [ a , c , b , d ] 或 [ c , a , b , d ] [a,c,b,d]或[c,a,b,d] [a,c,b,d]或[c,a,b,d]都是合理的。 D F S DFS DFS和 B F S BFS BFS都可以实现拓扑排序
3.基于 B F S BFS BFS的拓扑排序
基于
B
F
S
BFS
BFS的拓扑排序有两种思路:1. 无前驱的顶点优先、2. 后继的顶点优先。
下面先讲解无前驱的顶点优先拓扑排序。其方法是先输出出度为
0
0
0 (无前驱,优先级最高)点,具体操作如下图所示,其中
Q
Q
Q 是
B
F
S
BFS
BFS的队列:

步骤简述如下:
- 找到所有入度为 0 0 0 的点,放进队列,作为起点,这些点谁先谁后没有关系。如果找不到入度为 0 0 0的点,说明这个图不是 D A G DAG DAG,不存在拓扑排序。上图1中 a 、 c a、c a、c的入度为 0 0 0,进队列。
- 弹出队首 a a a, a a a的所有邻居点,入度减 1 1 1,把入度减为 0 0 0 的邻居点 b b b 放进队列,没有减为 0 0 0的点不能放进队列。如上图2。
- 继续上述操作,直到队列为空。内容见上图后续。队列输出 a c b d acbd acbd,而且包含了所有的点,这就是一个拓扑排序。
- 如果队列已空,但是还有点未进入队列,那么这些点的入度都不是 0 0 0,说明图不是 D A G DAG DAG,不存在拓扑排序。
以上是“无前驱”的思路。读者很容易发现,这个过程可以反过来执行,即“无后继的顶点优先”:从出度为
0
0
0(无后继,优先级最低)的点开始,逐步倒推。其示意图如下所示,请读者自己分析过程。最后输出的是逆序
[
d
,
b
,
c
,
a
]
[d,b,c,a]
[d,b,c,a]。
复杂度分析
在初始化时,查找入度为 0 0 0的点,需要检查每个边,复杂度为 O ( E ) O(E) O(E);在队列操作中,每个点进出队列一次,需要检查它直接连接的所有邻居,复杂度是 O ( V + E ) O(V+E) O(V+E)。其总复杂度是 O ( V + E ) O(V+E) O(V+E)
4.基于 D F S DFS DFS搜索的拓扑排序
D
F
S
DFS
DFS天然适合拓扑排序。
回顾
D
F
S
DFS
DFS深度搜索的原理:沿着一条路径一直搜索到最底层,然后逐层回退。这个过程正好体现了点和点的先后关系,天然符合拓扑排序的原理。
一个有向无环
D
A
G
DAG
DAG图,如果只有一个点
u
u
u是
0
0
0入度的,那么从
u
u
u开始
D
F
S
DFS
DFS,
D
F
S
DFS
DFS递归返回的顺序就是拓扑排序(是一个逆序)。
D
F
S
DFS
DFS递归返回的首先是最底层的点,它一定是
0
0
0出度点,没有后续点,是拓扑排序的最后一个点;然后逐步回退,最后输出的是起点
u
u
u;输出的顺序是一个逆序。
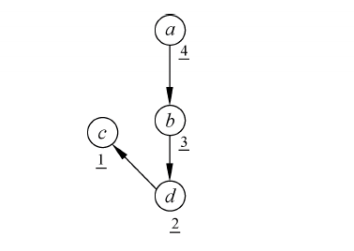
以上图为例,从
a
a
a 开始,递归返回的顺序见点旁边画线的数字,即
[
c
,
d
,
b
,
a
]
[c,d,b,a]
[c,d,b,a],是拓扑排序的逆序。为了按正确的顺序打印出拓扑排序,编程时的处理是定义一个拓扑排序队列
l
i
s
t
list
list,每次递归输出的时候把它插到当前
l
i
s
t
list
list的最前面,最后从头到尾打印
l
i
s
t
list
list,就是拓扑排序。这实际上是一个栈,直接用STL的stack即可。
细节处理
- 应该以入度为
0
0
0的点为起点开始
D
F
S
DFS
DFS。如何找到它?需要找到它吗?如果有多个入度为
0
0
0的点呢?
这几个问题其实并不用特别处理。想象有一个虚拟的点 v v v,它单向连接到所有其他点。这个点就是图中唯一的 0 0 0入度点,图中所有其他的点都是它的下一层递归,而且它不会把原图变成环路。从这个虚拟点开始 D F S DFS DFS就完成了拓扑排序。
例如 图 ( a ) 图(a) 图(a)有两个 0 0 0入度点 a a a和 f f f。 图 ( b ) 图(b) 图(b)想象有个虚拟点 v v v,那么递归返回的顺序见点旁边画线的数字,返回的是拓扑排序的逆序。
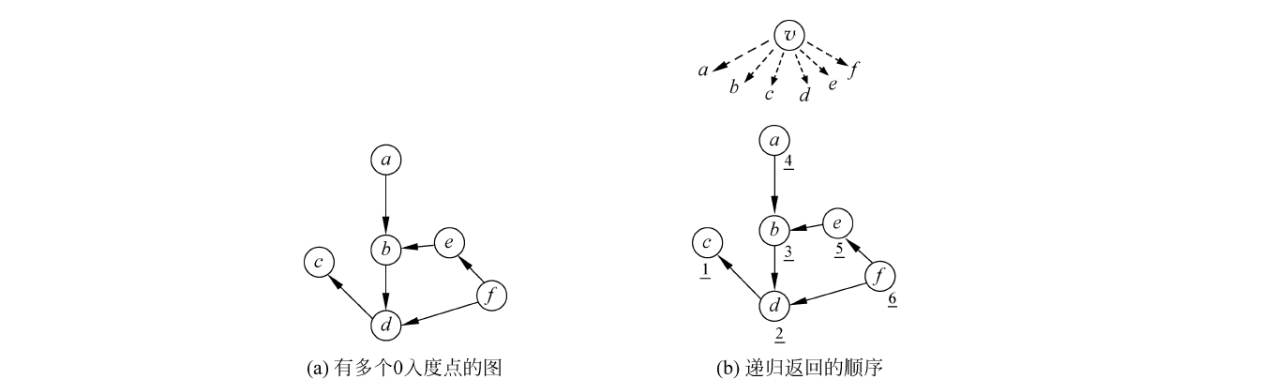
在实际编程的时候并不需要处理这个虚拟点,只要在主程序中把每个点轮流执行一遍 D F S DFS DFS即可。这样做相当于显式地递归了虚拟点的所有下一层点。 - 如果图不是
D
A
G
DAG
DAG,能判断吗?
图不是DAG,说明图是有环图,不存在拓扑排序。那么在递归的时候会出现回退边。如果读者不理解这一点,请回顾上一节的内容。在程序中这样发现回退边:记录每个点的状态,如果 d f s ( ) dfs(\ ) dfs( )递归到某个点时发现它仍在前面的递归中没有处理完毕,说明存在回退边,不存在拓扑排序。 - 如果要按照字典序输出同优先级的节点呢?只需要在 B F S BFS BFS中把队列换成优先队列即可。