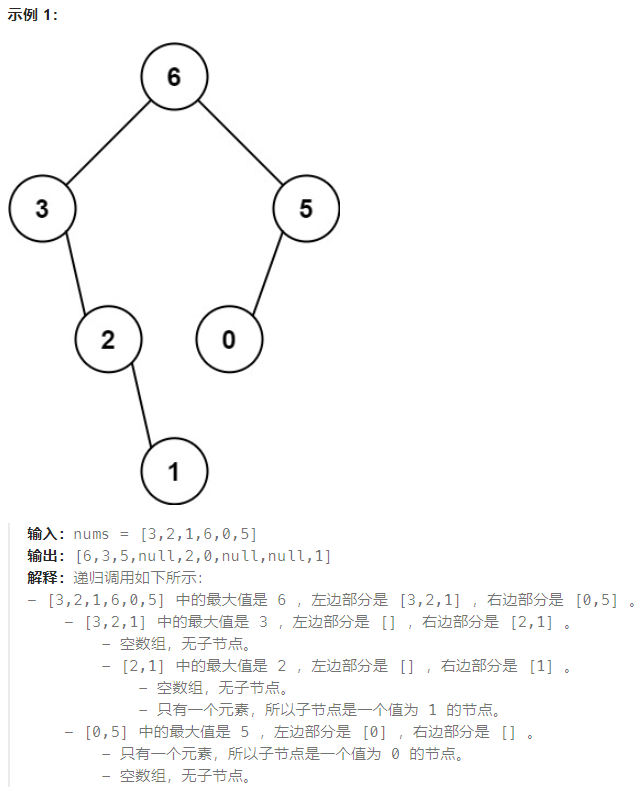
构造二叉树: 使用前序遍历
已理解思路

虽然开辟额外空间, 但结果依旧受到原来的数影响(当为null时直接借用了原来数的节点)

class Solution {
public:
    TreeNode* mergeTrees(TreeNode* root1, TreeNode* root2) {
        if (root1 == nullptr) return root2;
        if (root2 == nullptr) return root1;

        TreeNode* tem = new TreeNode();
        tem->val += root1->val;
        tem->val += root2->val;

        tem->left = mergeTrees(root1->left, root2->left);
        tem->right = mergeTrees(root1->right, root2->right);

        return tem;
    }
};

你需要在 BST 中找到节点值等于 val 的节点。 返回以该节点为根的子树。 如果节点不存在，则返回 null

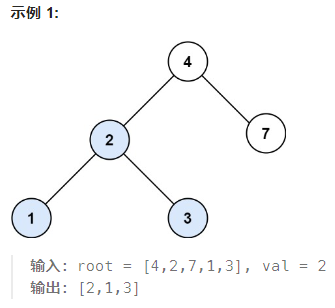
需要利用二叉搜索树的性质

• 
• 如果 root->val < val, 往右搜索
• 如果 root->val > val, 往左搜索

//当寻找到值时, 会立刻弹栈返回
class Solution {
public:
    TreeNode* searchBST(TreeNode* root, int val) {
        if (root == nullptr) return nullptr;

        TreeNode* result = nullptr;
        if (root->val < val) {
            result = searchBST(root->right, val);
        } else if (root->val > val) {
            result = searchBST(root->left, val);
        } else {
            result = root;
        }
        return result;
    }
};

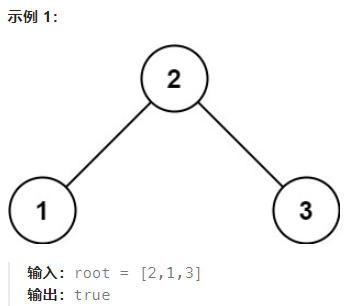
备注:

• 在中序遍历下, 输出的数组是一个递增数组, 只需要验证是否是递增即可

• 不能只比较左节点小于中间节点, 右节点大于中间节点

• 需要比较的是左子树所有节点小于中间节点, 右子树所有节点大于中间节点

• 

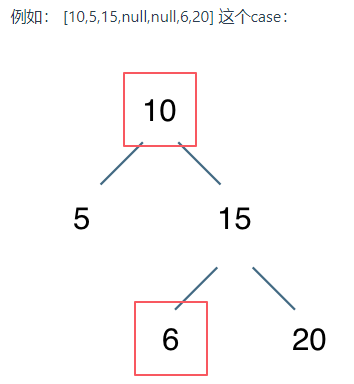
• 什么时候需要返回值

• 

思路: 暴力解法
直接中序遍历构造数组即可

思路: 递归解法

//使用最小值标志
class Solution {
public:
    // int pre_val = INT_MIN;
    long long pre_val = numeric_limits<long long>::min();
    bool isValidBST(TreeNode* root) {
        if (root == nullptr) return true;

        bool res1 = isValidBST(root->left);

        if (pre_val < root->val) { // 从小到大!!!
            pre_val = root->val;
        } else {
            return false;
        }

        bool res2 = isValidBST(root->right);

        return res1 && res2;
    }
};

//避免使用最小值
class Solution {
public:
    TreeNode* pre = nullptr;
    bool isValidBST(TreeNode* root) {
        if (root == nullptr)
            return true;

        bool res1 = isValidBST(root->left);

        if (pre == nullptr) {
            pre = root;
        } else if (pre->val < root->val) {
            pre = root;
        } else {
            return false;
        }
	
		//简便写法
	 	//if (pre != NULL && pre->val >= root->val) return false;
        //pre = root; // 记录前一个节点

        bool res2 = isValidBST(root->right);

        return res1 && res2;
    }
};