算法基础精选题单枚举 (合适的枚举顺序+合适的枚举内容+前缀和和差分) (个人题解)

前言：

今日第一份题解，题目主要是于枚举有关，枚举算是算法题中较为简单的部分了~~（对我来说还是有些难想的）~~，话不多说，见下。

正文：

题单：237题】算法基础精选题单_ACM竞赛_ACM/CSP/ICPC/CCPC/比赛经验/题解/资讯_牛客竞赛OJ_牛客网 (nowcoder.com)

合适的枚举内容：

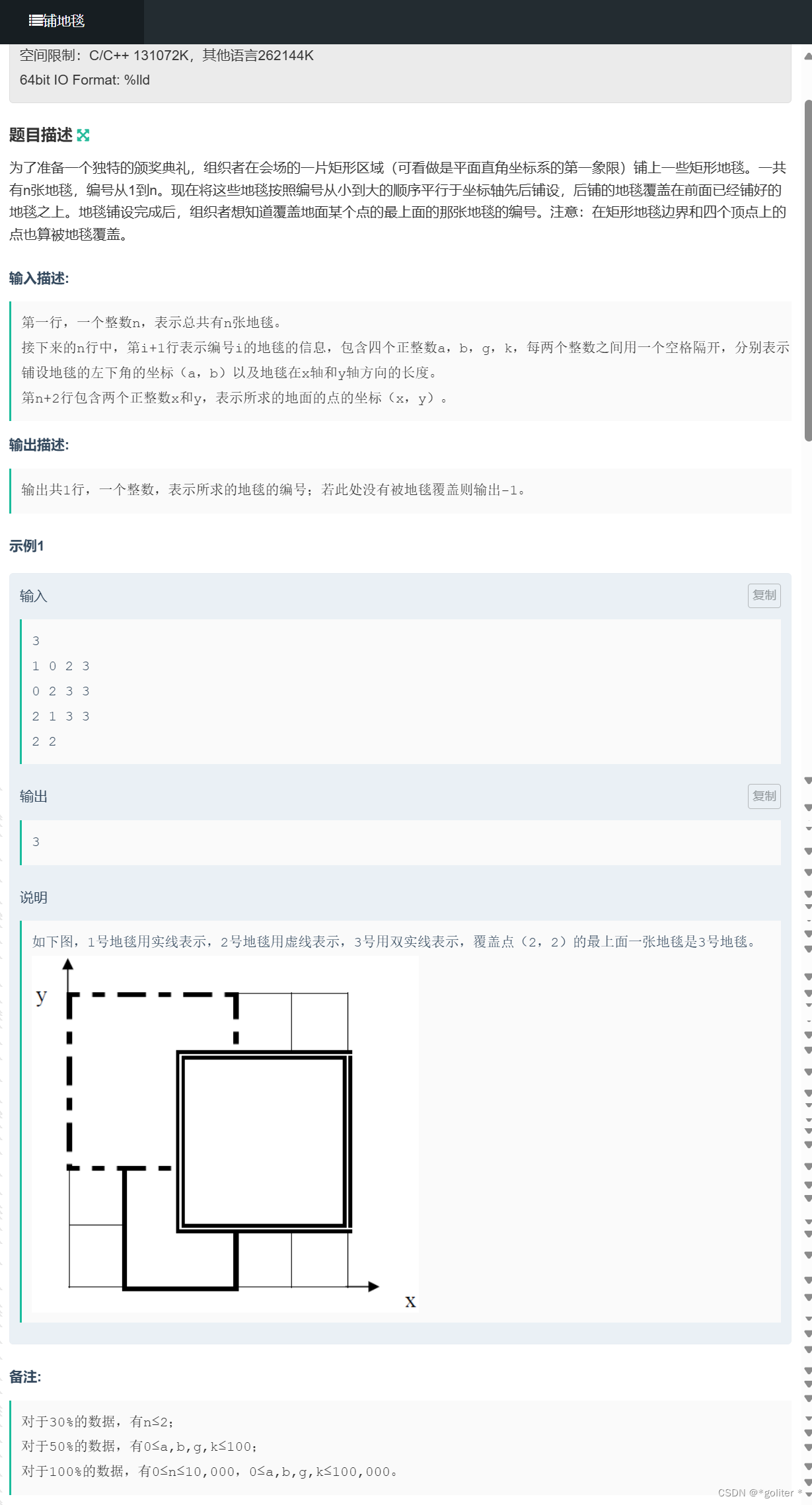
NC16593 [NOIP2011]铺地毯：

#include<bits/stdc++.h>
using namespace std;
int a[10000][4];
int main(){
	int n;
	cin>>n;
	for(int i=1;i<=n;i++){
		cin>>a[i][0]>>a[i][1]>>a[i][2]>>a[i][3];
	}
	int x,y;
	cin>>x>>y;
	for(int i=n;i;i--){
		if(x>=a[i][0]&&x<=a[i][0]+a[i][2]&&y>=a[i][1]&&y<=a[i][1]+a[i][3]){
			cout<<i<<endl;
			return 0;
		}
	}
	cout<<-1<<endl;
	return 0;
}

一开始像要开个数组模拟过程，但明显会超时，又想到查询只有一次，那么我们便可以从最后铺上的地毯开始向前枚举，如果按这个顺序枚举到了就一定是答案，如果到尾都没枚举到就是没地毯。

合适的枚举内容：

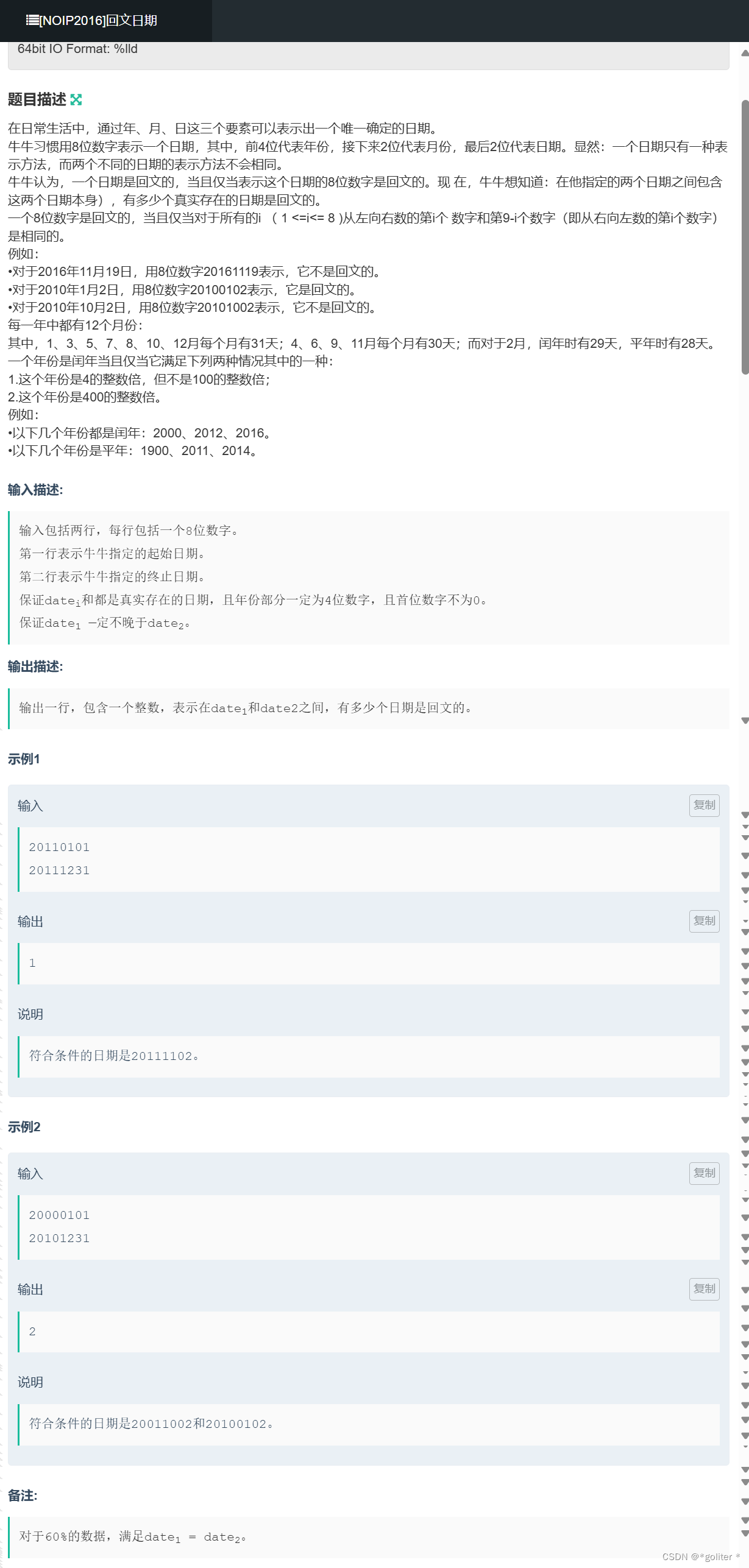
NC16438 回文日期：

#include<bits/stdc++.h>
using namespace std;
bool islunar(int y){
	return (y%4==0&&y%100!=0)||(y%400==0);
}
bool check(int year,int month,int day){
	if(month>12||month==0) return false;
	if(day>31) return false;
	if(month==2){
		if(islunar(year)&&day>29)
		return false;
		if(!islunar(year)&&day>28)
		return false;
	}
	if(month==4||month==6||month==9||month==11){
		if(day>30) return false;
	}
	return true;
}
int main()
{
    int x,y,i,ans=0;
    cin>>x>>y;
    int a,b,c,d,e,f,g,h;//8位数字
    int year,month,day;
    bool flag=false;
    for(i=x;i<=y;i++){
        year=i/10000;
        month=(i%10000)/100;
        day=i%100;
        a=i%10;
        b=(i/10)%10;
        c=(i/100)%10;
        d=(i/1000)%10;
        e=(i/10000)%10;
        f=(i/100000)%10;
        g=(i/1000000)%10;
        h=(i/10000000)%10;
        if(a==h&&b==g&&c==f&&d==e){
            if(check(year,month,day)){
                ans++;
            }
        }
    }
    cout<<ans<<endl;
    return 0;
}

模拟时间推进的过程，在枚举过程中判断回文并计数。

前缀和和差分：

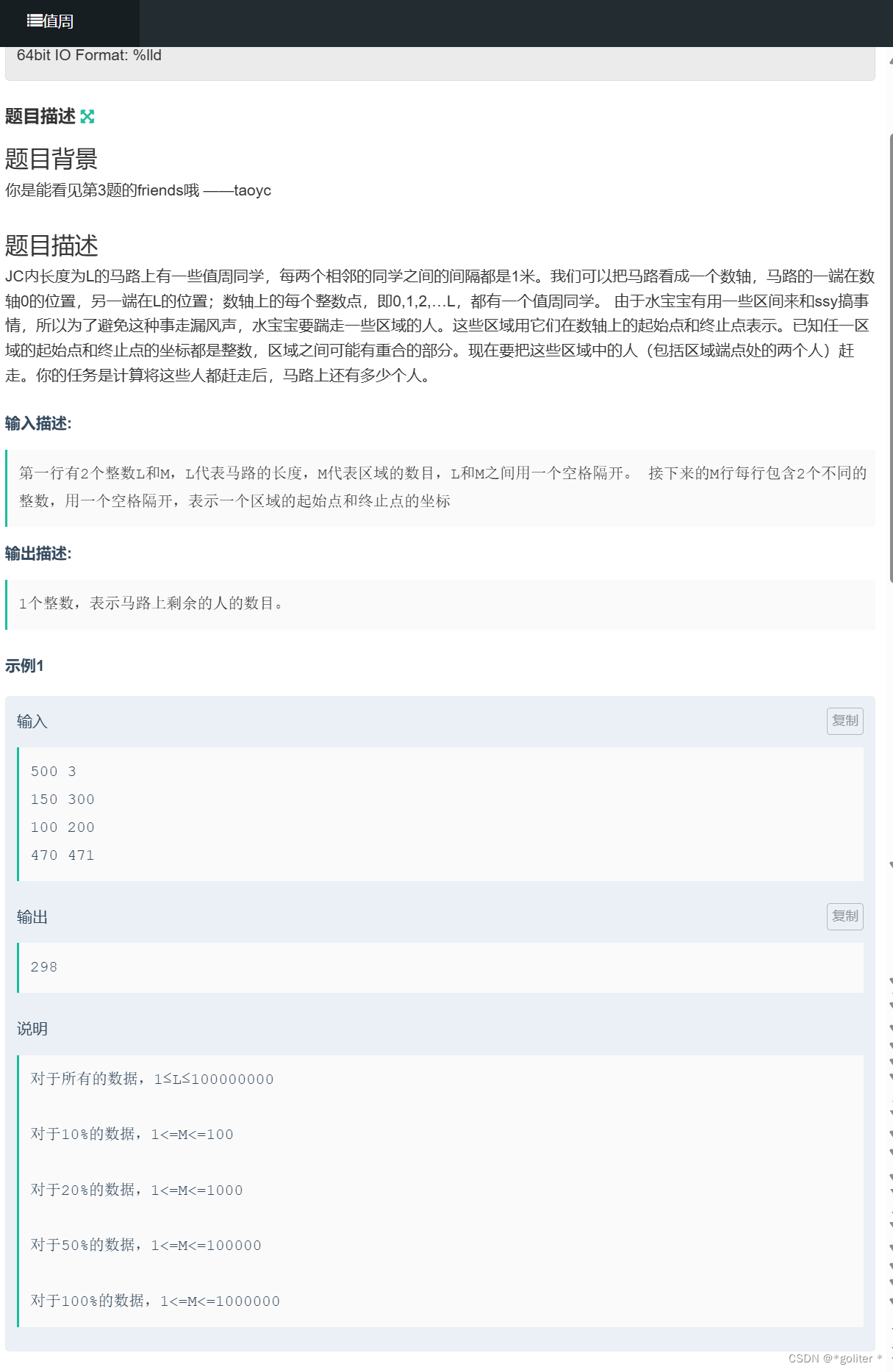
NC16649 校门外的树+NC24636 值周：

#include<bits/stdc++.h>
using namespace std;
int a[100000005];
int main(){
	int l,m,ans=0;
	cin>>l>>m;
	for(int i=0;i<=m;i++){
		int x,y;
		cin>>x>>y;
		a[x]++;a[y+1]--;
	}
	for(int i=0;i<=l;i++){
		a[i]+=a[i-1];
		if(a[i]==0)ans++;
	}
	cout<<ans<<endl;
	return 0;
}

两个题题目大意相同，但数据范围不同，这边直接放上数据大的题，这题用差分可以很好写出来，只要找出差分数组的前缀和数组中值为0的个数就为答案。

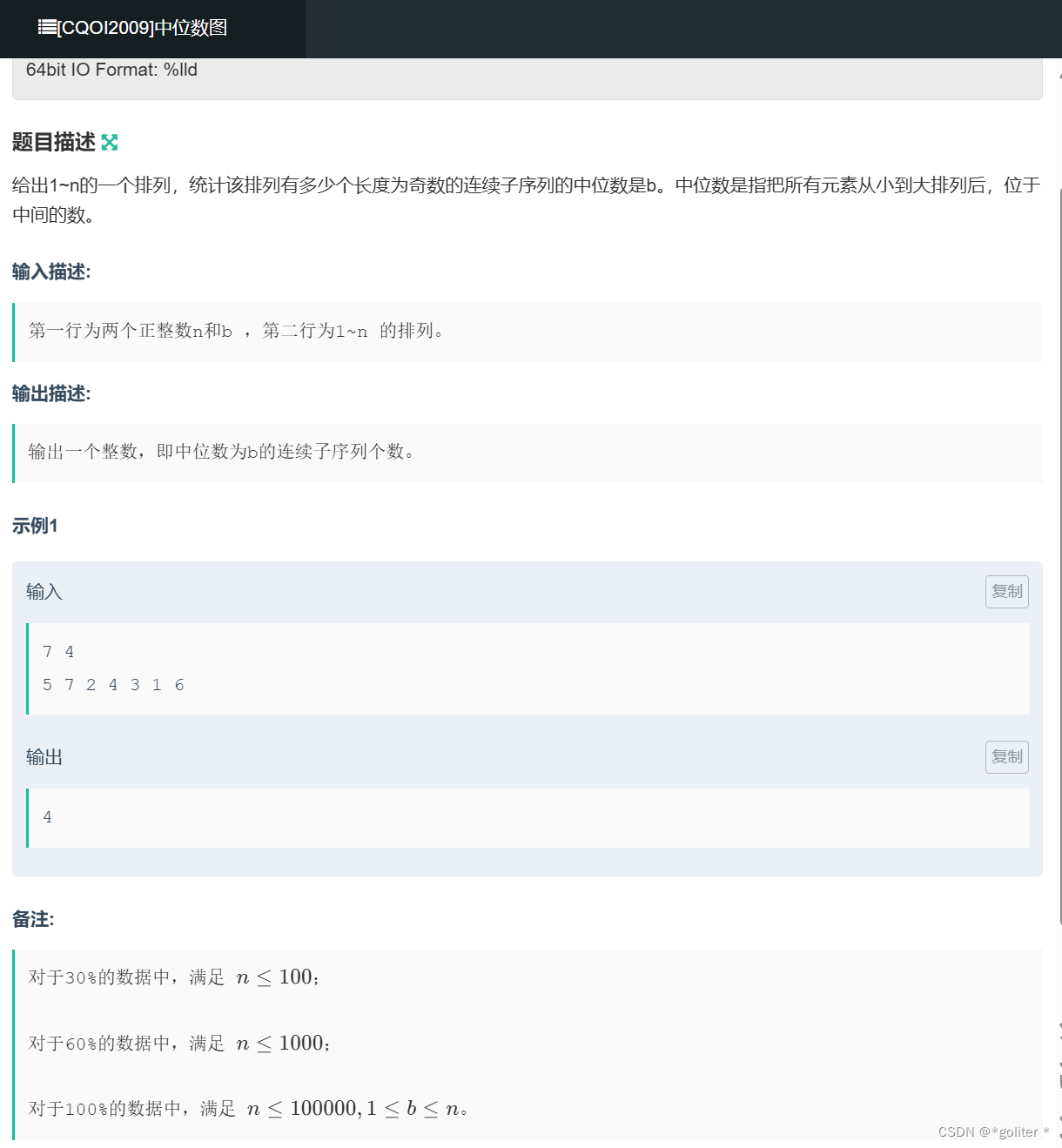
[CQOI2009]中位数图：

#include<bits/stdc++.h>
using namespace std;
int a[100005],l[100005],r[100005],aa[200005];
int n,b;
int main(){
	int res;
	cin>>n>>b;
	for(int i=1;i<=n;i++){
		cin>>a[i];
		if(a[i]>b)a[i]=1;
		else if(a[i]==b)res=i;
		else a[i]=-1;
	}
	int sum=0,ans=1;
	for(int i=res-1;i>=1;i--){
		sum+=a[i];
		aa[n+sum]++;
		if(sum==0)ans++;
		//cout<<sum<<endl;
	}
	sum=0;
	for(int i=res+1;i<=n;i++){
		sum+=a[i];
		ans+=aa[n-sum];
		if(sum==0)ans++;
		//cout<<sum<<endl;
	}
	cout<<ans<<endl;
	return 0;
}

这题要求中位数为b的子序列，因为子序列个数为奇数，所以子序列中一定含有b，所以我们只用讨论包含b的子序列，不妨先确定b在子序列中，在分别向两边讨论，我们将大于b的数变为1，小于的变为-1，所以只要这段序列的和为0（不包含b）即为答案的一种情况。这边要讨论两种，一种是一边为0，一种是两边之和为0，最后求出的即为答案。

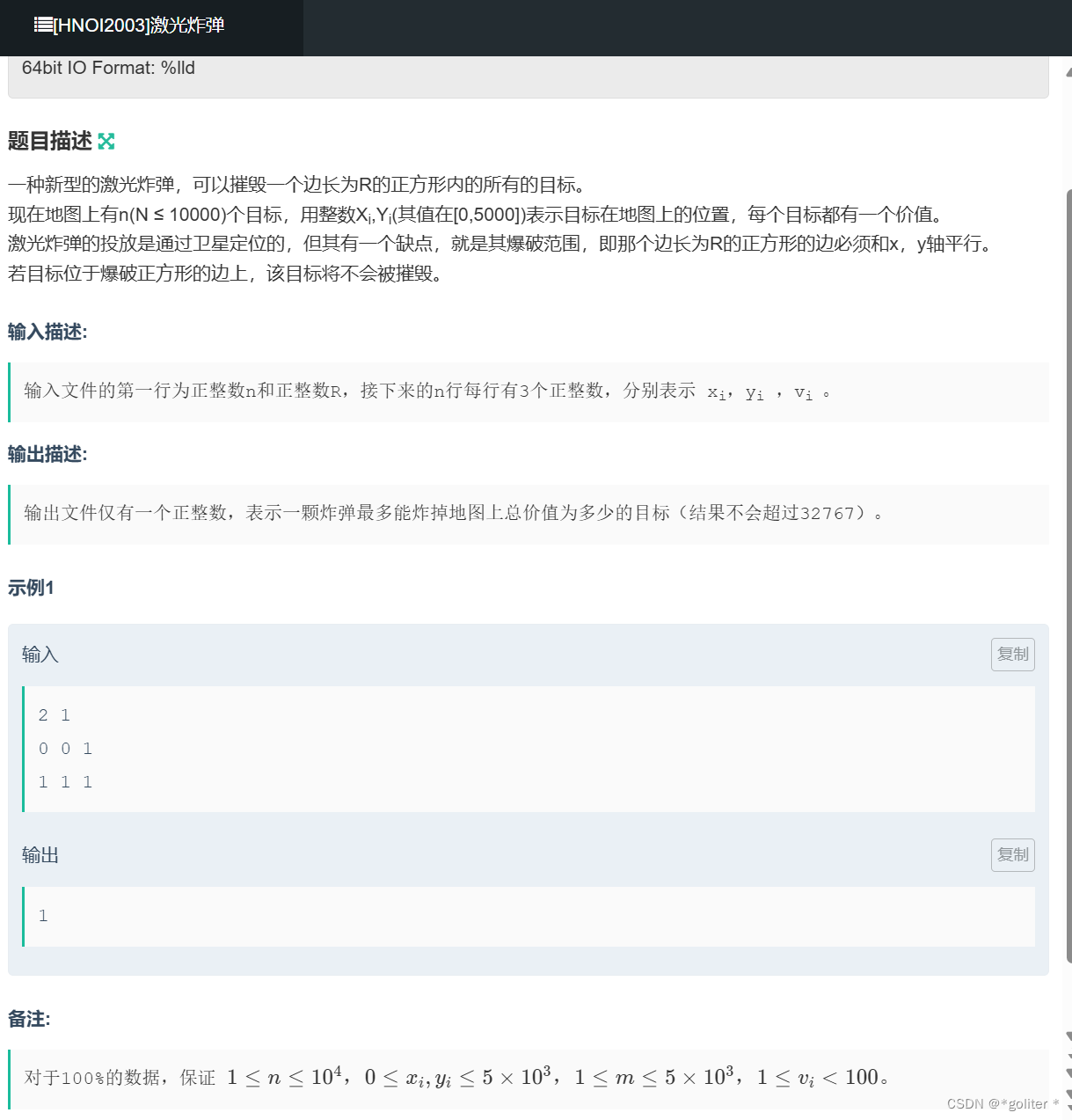
NC20032 激光炸弹：

#include<bits/stdc++.h>
using namespace std;
int a[5005][5005];
int main(){
	int n,r,ans=0;
	cin>>n>>r;
	for(int i=1;i<=n;i++){
		int x,y,v;
		cin>>x>>y>>v;
		a[x][y]+=v;
		//cout<<a[x][y]<<endl;
	}
	for(int i=0;i<=5000;i++){
		for(int j=0;j<=5000;j++){
			if(i==0&&j==0){
				a[i][j]=a[i][j];
			}
			else if(i==0)a[i][j]+=a[i][j-1];
			else if(j==0)a[i][j]+=a[i-1][j];
			else a[i][j]+=a[i-1][j]+a[i][j-1]-a[i-1][j-1];
			//cout<<a[i][j]<<" ";
			if(i>=r-1&&j>=r-1){
				if(i==r-1&&j==r-1)ans=max(a[i][j],ans);
				else if(i==r-1)ans=max(a[i][j]-a[i][j-r],ans);
				else if(j==r-1)ans=max(a[i][j]-a[i-r][j],ans);
				else ans=max(a[i][j]-a[i-r][j]-a[i][j-r]+a[i-r][j-r],ans);
			}
		}
		//cout<<endl;
	}
	cout<<ans;
	return 0;
}

通过二维前缀和来表示炸弹在该位置爆炸得到的价值，最后还原为爆炸范围大小的块来枚举答案，

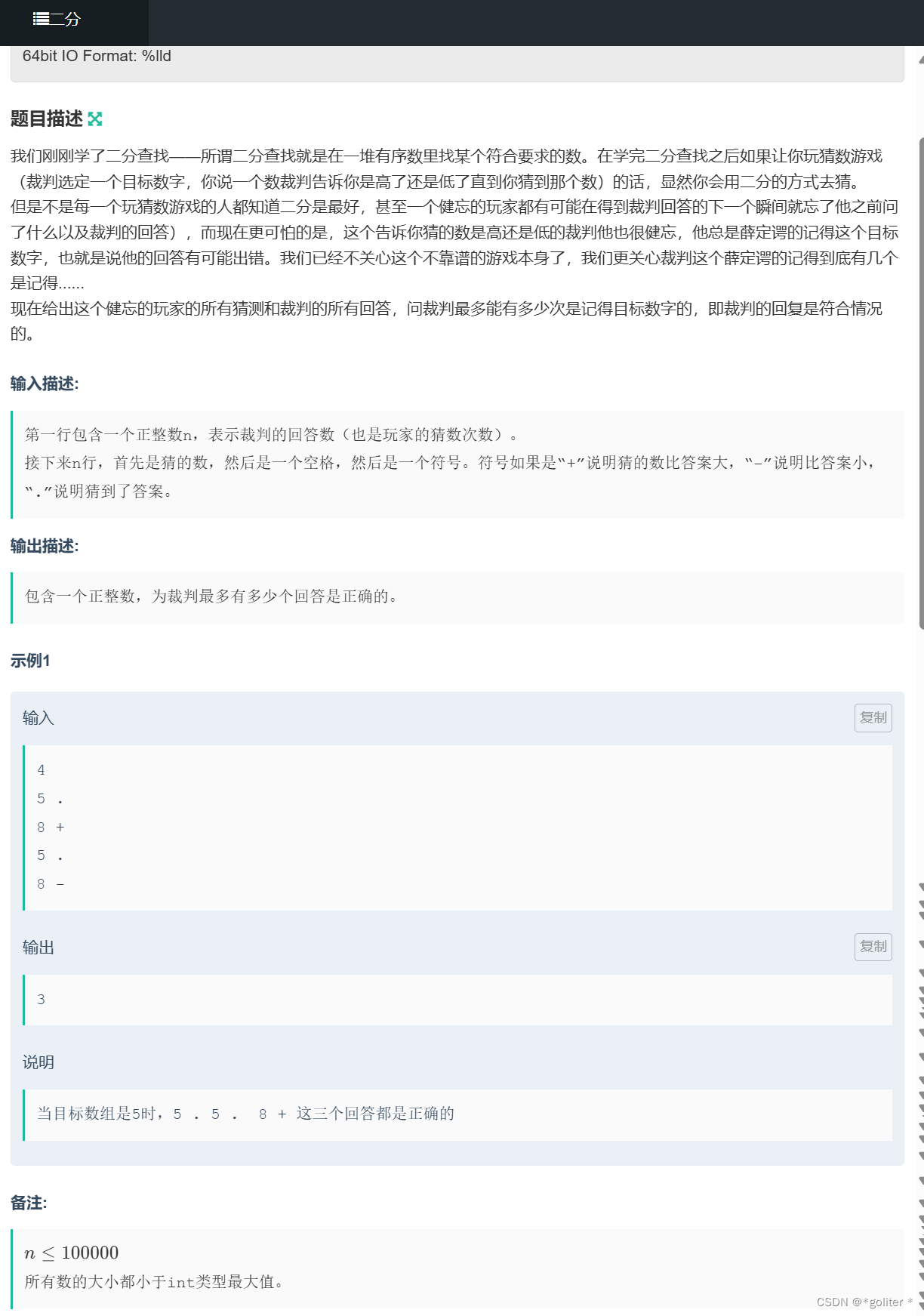
NC207053 二分：

#include<bits/stdc++.h>
using namespace std;
map<int,int> a;
int inf=0x3f3f3f3f;
int main(){
    int n;
    cin>>n;
    for(int i=0; i<n; i++){
        int x;
        char op;
        cin>>x>>op;
        if(op=='.')a[x]++,a[x+1]--;
        if(op=='+')a[x]--,a[-inf]++;
        if(op=='-')a[x+1]++;
    }
    int temp=0,ans=0;
    for(auto it:a){//遍历map
        temp+=it.second;//加上每个map对应的值
        ans=max(temp,ans);
    }
    cout<<ans<<endl;
    return 0;
}

这题和二分一点关系都没有，我们首先建立一个map来离散化的表示一个数组，数组的值表示该点满足的裁判所说话的数量，最后我们枚举map，最大的值就是裁判最多有多少个回答是正确的（因为该点可以满足这些情况）。最后数组我们就根据裁判的话来建立，如下

裁判说数大了，那么裁判说对的取值范围是(-∞,a]
裁判说数小了，那么裁判说对的取值范围是[a,+∞)
裁判说数一样，那么裁判说对的取值范围是[a,a]

最后得出答案。

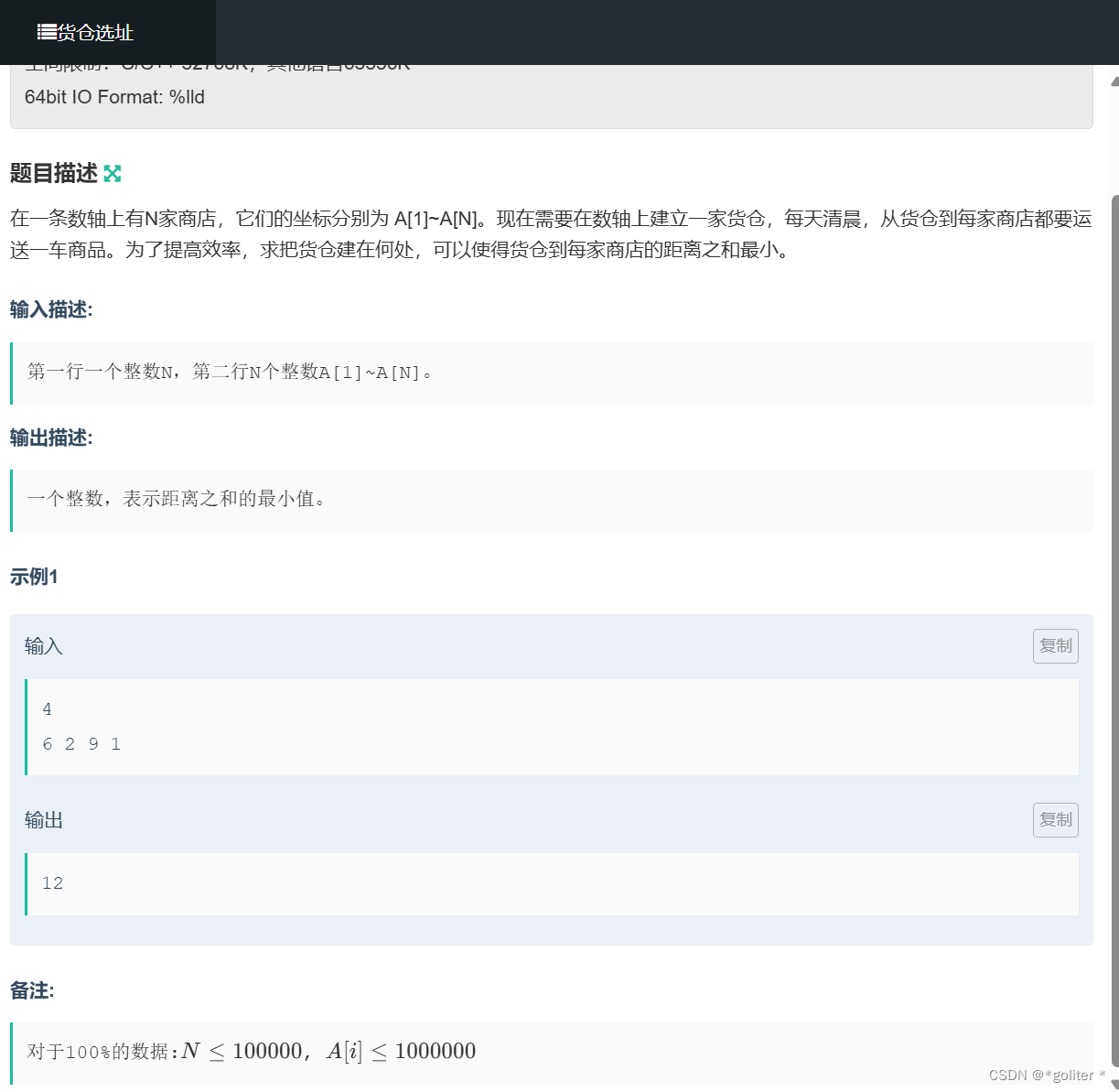
NC50937 货仓选址：

#include <bits/stdc++.h>
using namespace std;
const int N = 1e5 + 10;
int a[N];
int main(){
    int n;
    cin>>n;
    for(int i=0;i<n;i++)cin>>a[i];
    sort(a,a+n);
    int ans=0,l=0,r=n-1;
    while(l<r) 
        ans+=a[r--]-a[l++];
    cout<<ans;
    return 0;
}

将位置排序后知把货仓放在数组中间是正确的选择，如果为奇数则中间那个距离为0，剩下的两两配对（最小的和最大的，第二小的和第二大的）。最后易得答案。