大家好,我是微学AI,今天给大家介绍一下机器学习实战19-利用机器学习模型与算法实现销售数据的归因分析与图形生成。 归因分析是数据分析中的一个重要环节,它主要用于确定不同因素对特定结果(如销售额、转化率等)的贡献程度。在Python中,可以通过多种方式实现归因分析,包括使用现成的库和编写自定义函数。
文章目录
- 一、归因分析的基本概念
- 归因分析的方法
- 二、归因分析的实现步骤
- 归因分析步骤
- Python操作
- 代码实现
- 归因分析结果描述
- 三、Python中的其他归因分析库推荐
一、归因分析的基本概念
归因分析的目的是识别哪些因素对结果产生了显著影响。在市场营销领域,例如,可以通过归因分析来确定哪些广告渠道或营销活动对销售增长贡献最大。在医学研究中,可以通过归因分析来确定哪些因素对疾病发病率有显著影响。
归因分析的方法
在Python中,可以使用多种方法进行归因分析,包括:
风险比率(Risk Ratios):比较不同因素下的成功或失败的比例,以确定哪个因素的影响更大。
概率比率(Rate Ratios):类似于风险比率,但考虑了事件发生的总体概率。
机会比率(Odds Ratios):比较不同因素下事件发生的机会,通常用于替代风险比率和概率比率。
线性回归:通过构建线性模型来预测结果,并分析不同因素的系数大小来确定它们的贡献程度。
逻辑回归:适用于二分类问题,通过构建逻辑模型来预测结果,并分析不同因素的系数大小来确定它们的贡献程度。
二、归因分析的实现步骤
归因分析步骤
- 数据准备:首先,需要收集相关的数据,这些数据应该包括可能的因素(指标)以及结果。
- 指标贡献度计算:可以使用统计方法或机器学习模型来计算各个指标对结果的贡献度。例如,可以使用线性回归模型中的系数大小来表示每个指标的贡献度。
- 异常波动检测:可以通过设置阈值、使用统计测试(如假设检验)或机器学习模型(如孤立森林、LOF等)来检测指标的异常波动。
- 结果解释与决策:根据计算出的贡献度和异常波动检测结果,可以解释各指标对结果的影响,并据此做出决策。
接下来,我将使用样例数据来演示如何进行这些步骤。假设我们有以下数据集:
date:日期sales:销售额(结果变量)ad_spend:广告费用(指标1)discount:折扣率(指标2)holiday:是否节假日(指标3,0表示非节假日,1表示节假日)
Python操作
- 数据准备:创建样例数据集。
- 指标贡献度计算:使用线性回归模型计算
ad_spend、discount和holiday对sales的贡献度。 - 异常波动检测:使用IQR方法检测
ad_spend、discount和holiday的异常波动。 - 结果解释与决策:根据模型结果解释各指标的影响,并给出决策建议。
代码实现
import pandas as pd
import numpy as np
from sklearn.linear_model import LinearRegression
import matplotlib.pyplot as plt
#plt 显示中文
plt.rcParams['font.sans-serif'] = ['SimHei']
# 创建样例数据集
np.random.seed(0)
dates = pd.date_range('2023-01-01', periods=100)
sales = np.random.normal(1000, 200, 100) # 销售额
ad_spend = np.random.normal(500, 100, 100) # 广告费用
discount = np.random.normal(0.1, 0.05, 100) # 折扣率
holiday = np.random.choice([0, 1], 100) # 是否节假日
# 将数据合并为DataFrame
data = pd.DataFrame({
'date': dates,
'sales': sales,
'ad_spend': ad_spend,
'discount': discount,
'holiday': holiday
})
# 设置图形大小和分辨率
plt.figure(figsize=(14, 7), dpi=100)
# 绘制三条曲线
plt.plot(data['date'], data['sales'], label='Sales', color='blue')
plt.plot(data['date'], data['ad_spend'], label='Ad Spend', color='green')
# 添加标题和标签
plt.title('Sales,ad_spend 随时间的变化趋势')
plt.xlabel('Date')
plt.ylabel('Amount ')
plt.legend()
# 优化x轴日期显示,避免重叠
plt.xticks(rotation=45)
# 显示图形
plt.tight_layout() # 自动调整子图参数, 使之填充整个图像区域
plt.show()
# 线性回归模型计算贡献度
model = LinearRegression()
model.fit(data[['ad_spend', 'discount', 'holiday']], data['sales'])
contributions = model.coef_
# 异常波动检测
def detect_anomalies(data):
Q1 = data.quantile(0.25)
Q3 = data.quantile(0.75)
IQR = Q3 - Q1
anomalies = data[~((data >= Q1 - 1.5 * IQR) & (data <= Q3 + 1.5 * IQR))]
return anomalies
anomalies = {
'ad_spend': detect_anomalies(data['ad_spend']),
'discount': detect_anomalies(data['discount']),
'holiday': detect_anomalies(data['holiday'])
}
print(contributions)
print(anomalies)
# 使用matplotlib创建散点图
plt.figure(figsize=(10, 6))
# 区分节假日和非节假日
holiday_data = data[data['holiday'] == 1]
non_holiday_data = data[data['holiday'] == 0]
# 绘制散点图
plt.scatter(non_holiday_data['ad_spend'], non_holiday_data['sales'], c='blue', label='非节假日')
plt.scatter(holiday_data['ad_spend'], holiday_data['sales'], c='red', label='节假日')
# 添加标题和标签
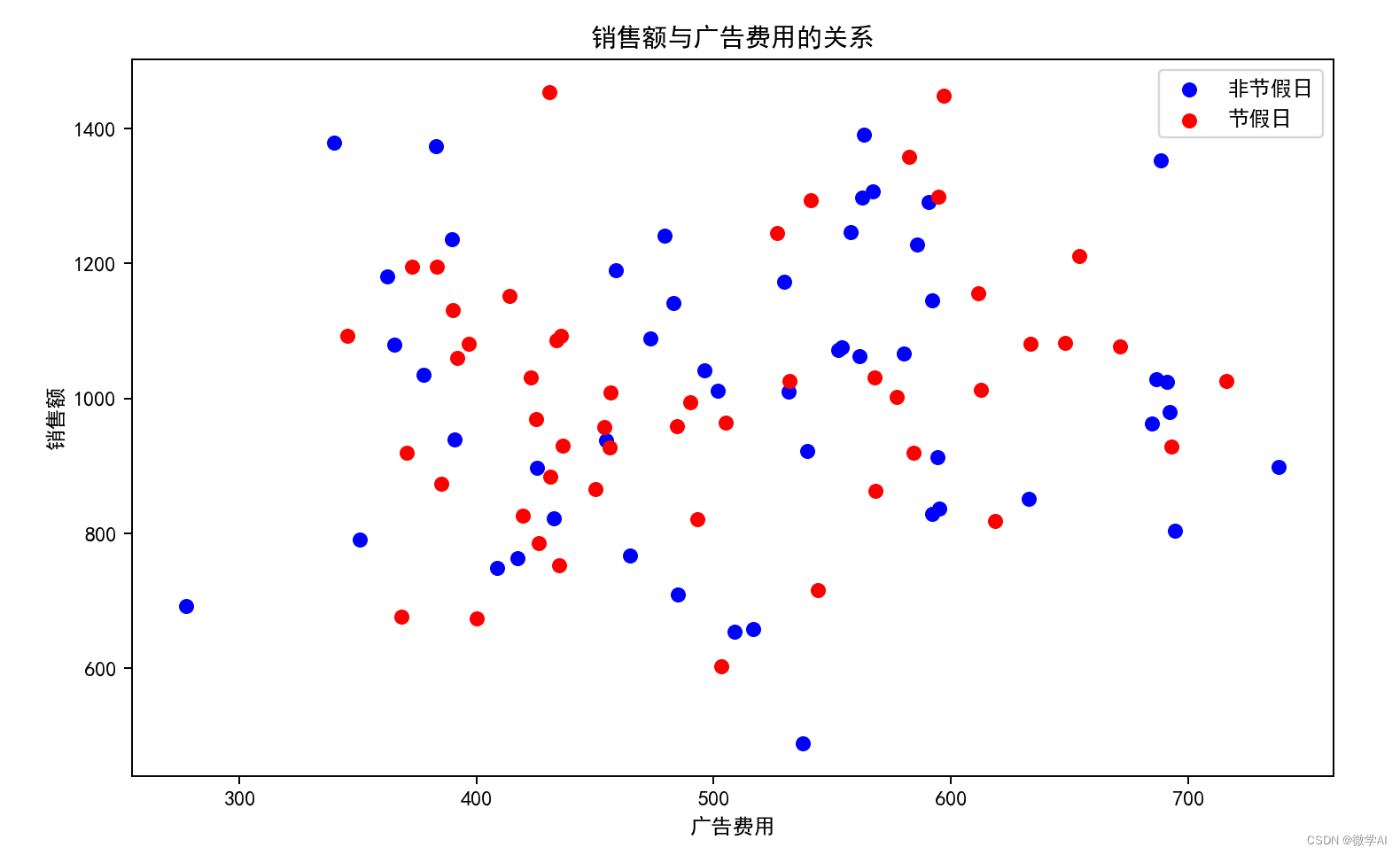
plt.title('销售额与广告费用的关系')
plt.xlabel('广告费用')
plt.ylabel('销售额')
plt.legend()
# 显示图表
plt.show()
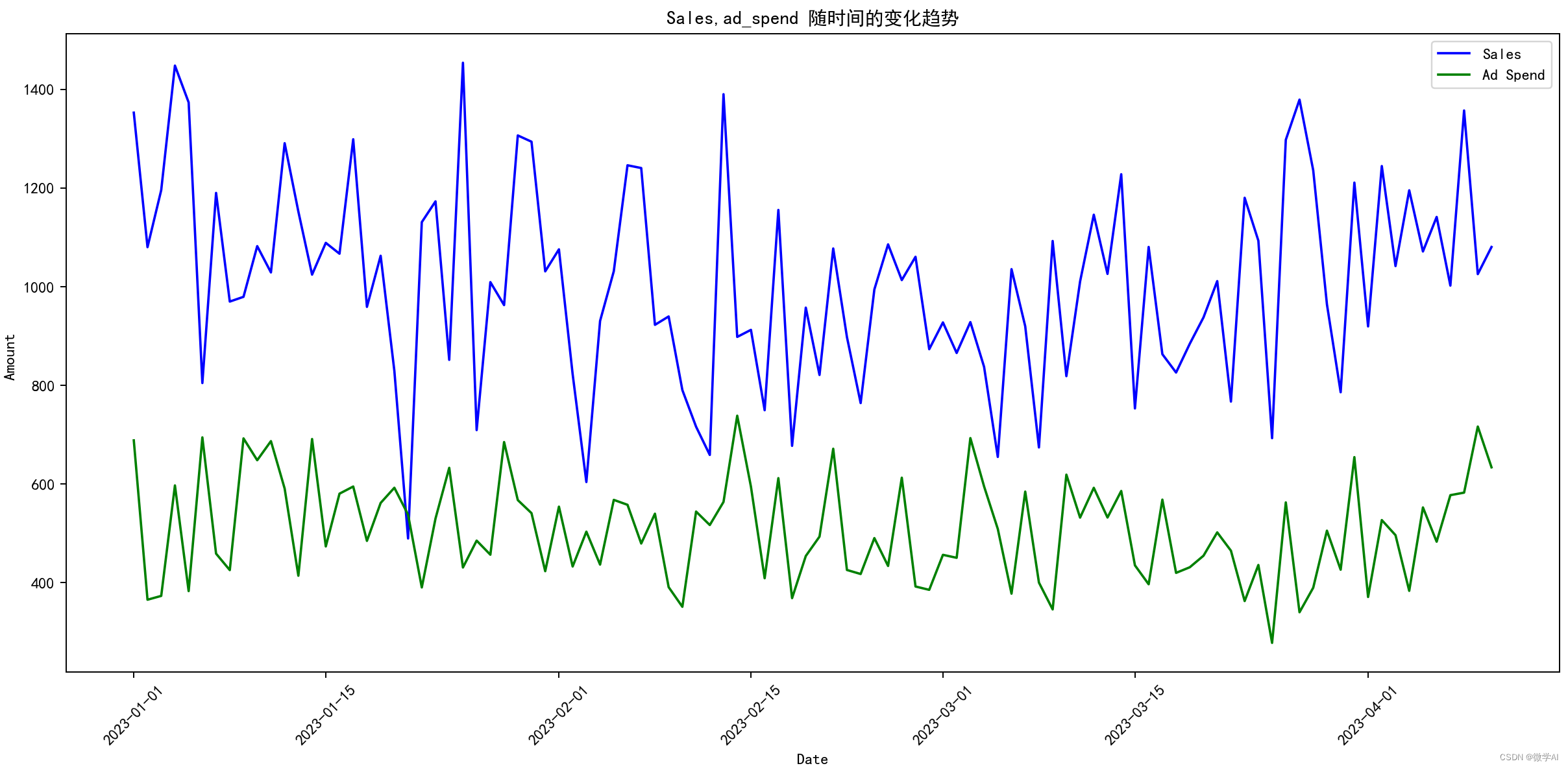
结果如下:
(array([2.12758894e-01, 3.02799610e+02, 5.86271391e+00]),
{‘ad_spend’: Series([], Name: ad_spend, dtype: float64),
‘discount’: 18 0.212965
71 -0.038630
92 0.215196
Name: discount, dtype: float64,
‘holiday’: Series([], Name: holiday, dtype: int64)})
归因分析结果描述
根据线性回归模型的结果,我们可以看到各指标对销售额(sales)的贡献度如下:
广告费用(ad_spend)的贡献度为
0.213
0.213
0.213(即每增加1单位的广告费用,销售额平均增加0.213单位)。
折扣率(discount)的贡献度为
302.8
302.8
302.8(即折扣率每增加1%,销售额平均增加302.8单位)。
是否节假日(holiday)的贡献度为
5.863
5.863
5.863(即如果是节假日,销售额平均增加5.863单位)。
对于异常波动检测,我们使用了IQR方法(四分位距),结果显示:
广告费用(ad_spend)和是否节假日(holiday)没有检测到异常波动。
折扣率(discount)在三个日期(索引为18、71和92)检测到了异常波动。
根据这些结果,我们可以解释各指标对销售额的影响,并据此做出决策。例如,增加广告费用和折扣率可能会提高销售额,尤其是在节假日。同时,需要注意折扣率的异常波动,这可能需要进一步的分析来理解其背后的原因。
三、Python中的其他归因分析库推荐
除了statsmodels和scikit-learn,Python生态中还有其他一些库可以用于进行归因分析。以下是一些较为知名的库:
PyMC:PyMC是一个用于贝叶斯统计建模和推断的Python库。它提供了大量的统计模型、采样器和可视化工具,可以帮助用户进行贝叶斯推断和概率编程。
Gensim:Gensim是一个用于主题建模、文档索引和大型文本数据集分析的Python库。它使用无监督学习算法来发现文本数据中的模式和结构。Gensim还提供了相似性搜索和文本生成等功能。
Orange:Orange是一个用于数据挖掘和可视化的Python库。它提供了大量内置的数据分析工具,如分类、聚类、回归和可视化等。Orange还提供了一个交互式的界面,使用户可以轻松地探索和分析数据。
PyMVPA:PyMVPA是一个用于多变量分析的Python库。它提供了大量的多变量分析算法,如主成分分析和独立成分分析等。PyMVPA还提供了数据预处理和特征选择等功能。
Theano:Theano是一个用于高性能数值计算的Python库。它使用符号式编程来定义和优化计算图,并支持GPU加速。Theano可以用于深度学习和机器学习等领域。
PyLearn:PyLearn是一个基于Theano的机器学习库。它提供了一个简洁的API来定义和训练神经网络,并支持多种神经网络架构。PyLearn还提供了数据预处理和模型评估等功能。
Hebel:Hebel是一个使用GPU加速的神经网络库。它使用纯Python编写,并提供了一个简洁的API来定义和训练神经网络。Hebel还支持自定义层和激活函数等功能。
Neurolab:Neurolab是一个基于神经网络的Python库。它提供了一个易于使用的API来实现各种神经网络架构,包括递归神经网络和长短期记忆网络等。Neurolab还支持多种优化算法和自定义层等功能。