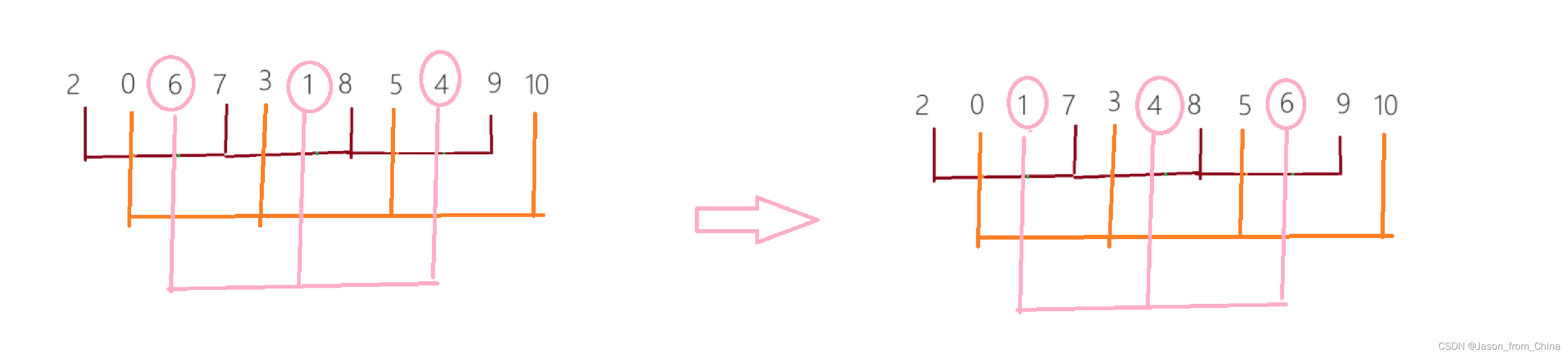前言
从希尔开始,排序的速度就开始上升了,这里的排序开始上一个难度了,当然难一点的排序其实也不是很难,当你对于插入排序了解的足够深入的时候,你会发现其实希尔就是插入的异形,但是本质上还是一样的
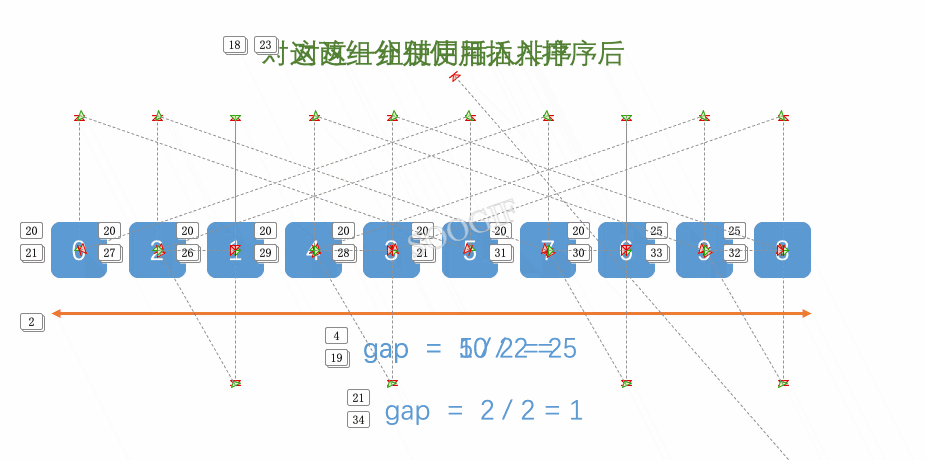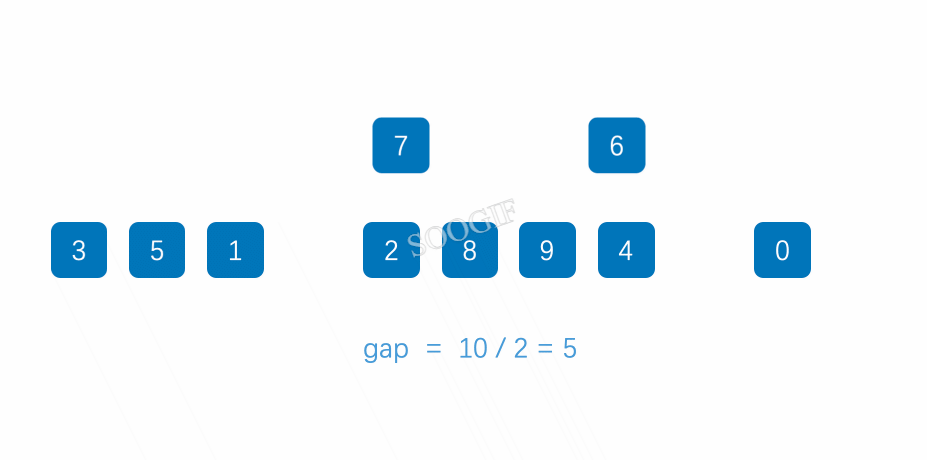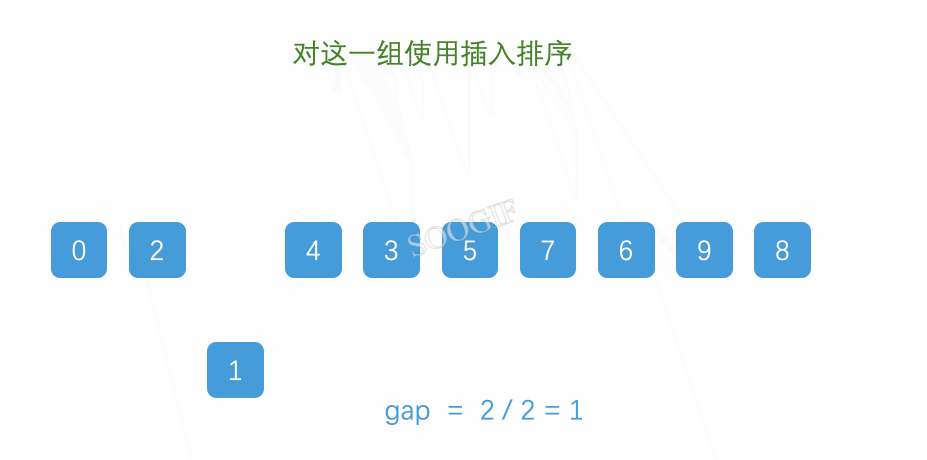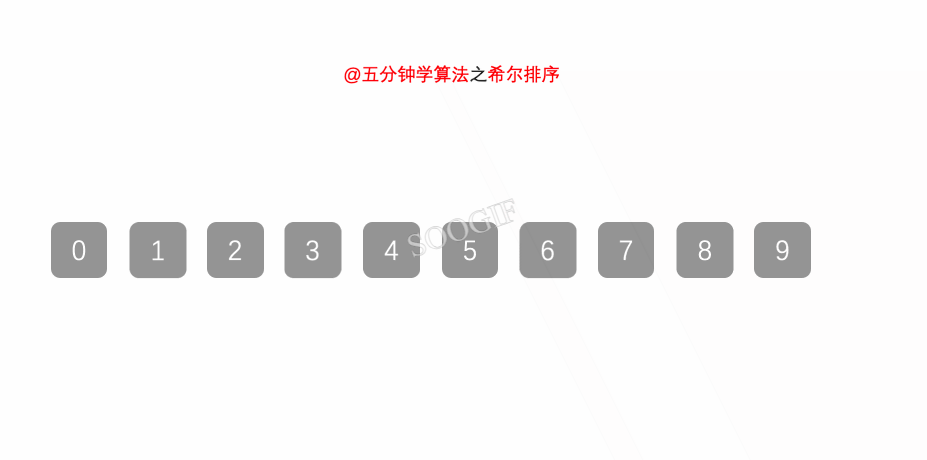
希尔排序gif
希尔排序单趟实现
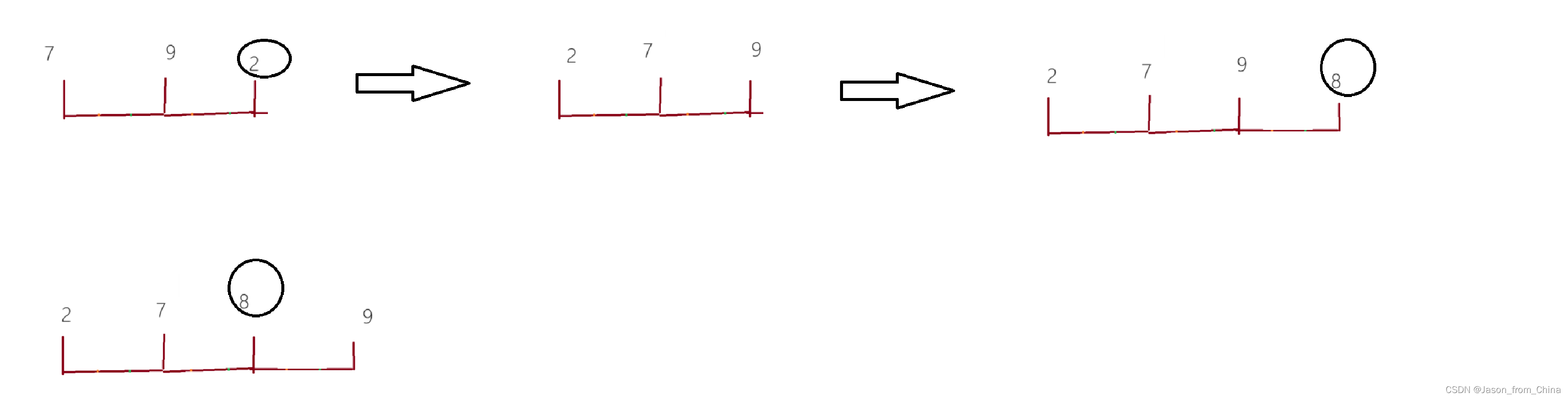
1,希尔排序本质就是插入排序的进化,插入排序是寻找比较进行插入,希尔这个人觉得插入排序有点慢,就觉得我们可不可以进行预排序,也就是数值原来是0-9的情况下,最坏的情况我们需要循环9次数才能找到需要插入的点在哪,那么此时我们能不能进行一个预排序
2,所谓的预排序就是,我们假设几个为一组,几个为一组,这个组的变量我们设置为gap。假设处置3个为一组,那么gap=3
3,此时我们可以把这一组,先采取插入排序的方式进行预排序,预排序之后我们就会发现这一组的这条线上的数值已经有序
4,多趟实现只是反复的实现第一趟的实现的逻辑
希尔排序的多趟实现
1,多趟实现只是反复的实现第一趟的实现的逻辑
2,我们需要先知道单趟遍历的时候,我们需要假设gap一组的,这个中间的元素是没有的,那么此时此时一组就是两个数值,我们需要让这两个数值进行交换
3,这两个数值交换之后我们这个时候需要循环开始插入排序的逻辑,也就是假设前面的两个数值是已经有序的,那么新插入的一个数值是需要排序的,我们进行排序
4,一趟结束之后,我们继续多趟实现,这几个数值继续预排序
5,继续预排序
6,此时gap=3,那么我们继续,gap/2=1,之后继续进行预排序,此时我们就得到了这个排序正确的数值
希尔排序代码的实现-版本1
//希尔排序 void ShellSort(int* a, int n) { int gap = n - 1; //定义gap,这里循环停止的条件是>1,原因是+1了,已经恒大于0了,所以需要大于1,等于都不可以 while (gap > 1) { gap = gap / 3 + 1; //循环实现每一组 for (int j = 0; j < gap; j++) { //gap单趟实现 for (int i = j; i < n - gap; i += gap) { int end = i; int tmp = a[end + gap]; //一组的实现 while (end >= 0) { if (tmp < a[end]) { a[end + gap] = a[end]; end -= gap; } else { break; } } //交换找到的数值 a[end + gap] = tmp; } } } }解释:
函数
ShellSort接受两个参数:一个指向整数数组a的指针和数组的长度n。初始化间隔
gap为数组长度n - 1,这是希尔排序开始时的最大间隔。
while循环用于逐步减小间隔,直到间隔为1。当gap大于1时,循环继续。在每次
while循环的开始,重新计算间隔gap。这里使用的是gap = gap / 3 + 1,这是一种常见的间隔序列,由Donald Shell提出。外层
for循环用于遍历数组,步长为当前的间隔gap。内层
for循环用于实现插入排序,但仅限于间隔gap内的范围。在内层循环中,
end变量记录当前考虑的元素的索引,tmp变量暂存当前要插入的元素。
while循环用于在间隔gap内从后向前扫描,找到tmp应该插入的位置。如果
tmp小于当前比较的元素a[end],则将a[end]向后移动一个间隔gap的距离,为tmp腾出空间。如果
tmp大于或等于a[end],则while循环结束,找到了tmp应该插入的位置。循环结束后,将
tmp赋值给a[end + gap],完成插入操作。这个过程重复进行,直到数组中的所有元素都被扫描并插入到正确的位置。
代码逻辑:
- 希尔排序通过多个插入排序的变体来工作,每个变体都有一个特定的间隔。
- 初始时,间隔较大,排序的稳定性较差,但可以快速减少无序度。
- 随着间隔逐渐减小,排序的稳定性逐渐提高,最终当间隔为1时,算法变为普通的插入排序,确保数组完全有序。
注意:
- 希尔排序不是稳定的排序算法,因为它可能会改变相等元素的相对顺序。
- 希尔排序的时间复杂度通常在 𝑂(𝑛log𝑛) 和 𝑂(𝑛^2) 之间,具体取决于间隔序列的选择。
- 希尔排序的空间复杂度是 𝑂(1,因为它是原地排序算法,不需要额外的存储空间。
希尔排序代码的实现-版本2
上面那个代码一般是教学使用,书写会更加详细理解,但是很多书本会这样写
这里的关键在于,不再进行先一组排序结束,再反过来进行下一组反复执行
而是直接这一组实现完毕之后,++,直接进行下一组的实现,本质上还是一样的
只是直接这样书写,容易不理解
//希尔排序 void ShellSort02(int* a, int n) { int gap = n - 1; //定义gap,这里循环停止的条件是>1,原因是+1了,已经恒大于0了,所以需要大于1,等于都不可以 while (gap > 1) { gap = gap / 3 + 1; //循环实现每一组+//gap单趟实现 for (int i = 0; i < n - gap; i++) { int end = i; int tmp = a[end + gap]; //一组的实现 while (end >= 0) { if (tmp < a[end]) { a[end + gap] = a[end]; end -= gap; } else { break; } } //交换找到的数值 a[end + gap] = tmp; } } }解释:
函数
ShellSort02接受两个参数:一个指向整数数组a的指针和数组的长度n。初始化间隔
gap为数组的最后一个索引n - 1。
while循环用于逐步减小间隔,直到间隔小于或等于1。循环的条件是gap > 1,这是因为间隔在每次迭代中都会减小,所以不需要检查gap == 1的情况。在
while循环内部,重新计算间隔gap。这里使用的计算方法是gap = gap / 3 + 1,这是一种常见的间隔序列,旨在逐步减小间隔,直到达到1。外层
for循环遍历数组,直到i < n - gap,即遍历到数组的末尾减去当前间隔的位置。在外层
for循环中,end变量记录当前考虑的元素的索引,tmp变量暂存当前间隔位置的元素值。内层
while循环用于在数组中找到tmp应该插入的位置。它从当前索引end开始,向前以间隔gap的距离进行比较。如果
tmp小于当前比较的元素a[end],则将a[end]向后移动一个间隔gap的距离,为tmp腾出空间。如果
tmp大于或等于a[end],则while循环结束,找到了tmp应该插入的位置。循环结束后,将
tmp赋值给a[end + gap],完成插入操作。这个过程重复进行,直到数组中的所有元素都被扫描并插入到正确的位置。
代码逻辑:
- 希尔排序通过多个插入排序的变体来工作,每个变体都有一个特定的间隔。
- 初始时,间隔较大,随着算法的进行,间隔逐渐减小,直到变为1,此时算法变为普通的插入排序。
- 通过逐步减小间隔,希尔排序能够在每次迭代中对数组的更大范围内的元素进行排序,从而减少比较和移动的次数。
希尔排序gap的界定
一般来说,一组为多少这个不好说,希尔开始书写的时候,gap是/2,来进行书写的,但是被认为效率最高的是,除以3+1,但是/3+1有一个弊端就是这个是恒大于0的,所以终止条件应该换为大于1就继续循环,小于等于1就停止循环
希尔排序的时间复杂度
希尔排序的时间复杂度取决于所选择的间隔序列,它通常介于以下范围:
最好情况:对于某些特定的间隔序列,希尔排序可以达到O(nlogn) 的时间复杂度,这与快速排序或归并排序相当。
平均情况:平均情况下,希尔排序的时间复杂度通常被认为是 O(n(logn)2),这比=O(nlogn) 稍差,但仍然比普通插入排序的 𝑂(𝑛^2) 好得多。
最坏情况:最坏情况下,希尔排序的时间复杂度可以退化到𝑂(𝑛^2),这通常发生在间隔序列选择不佳时。
实际性能:在实际应用中,希尔排序的性能通常比普通插入排序好,但不如快速排序、堆排序或归并排序。它的实际性能还取决于数据的初始状态和间隔序列的选择。
间隔序列的影响:不同的间隔序列对希尔排序的性能有很大影响。例如,使用Hibbard 间隔序列或Sedgewick间隔序列可以提高性能,有时甚至可以达到接近 O(nlogn) 的效率。
空间复杂度:希尔排序是原地排序算法,其空间复杂度为 𝑂(1)。
稳定性:希尔排序不是稳定的排序算法,这意味着相等的元素在排序后可能会改变它们原来的顺序。
总的来说,希尔排序是一种有效的排序算法,特别是对于中等大小的数据集或者当数据已经部分有序时。然而,对于大型数据集,通常推荐使用其他更高效的排序算法,如快速排序、堆排序或归并排序。