1.下一个排列
31. 下一个排列 - 力扣(LeetCode)
整数数组的一个 排列 就是将其所有成员以序列或线性顺序排列。
- 例如,
arr = [1,2,3],以下这些都可以视作arr的排列:[1,2,3]、[1,3,2]、[3,1,2]、[2,3,1]。整数数组的 下一个排列 是指其整数的下一个字典序更大的排列。更正式地,如果数组的所有排列根据其字典顺序从小到大排列在一个容器中,那么数组的 下一个排列 就是在这个有序容器中排在它后面的那个排列。如果不存在下一个更大的排列,那么这个数组必须重排为字典序最小的排列(即,其元素按升序排列)。
- 例如,
arr = [1,2,3]的下一个排列是[1,3,2]。- 类似地,
arr = [2,3,1]的下一个排列是[3,1,2]。- 而
arr = [3,2,1]的下一个排列是[1,2,3],因为[3,2,1]不存在一个字典序更大的排列。给你一个整数数组
nums,找出nums的下一个排列。
首先要了解字典序是什么
【算法】字典序超详细解析(让你有一种相见恨晚的感觉!)-CSDN博客
即就是每个字符串的字符挨个进行比较
方法一:两遍扫描
我们观察这一组数
我们注意到下一个排列总是比当前排列要大,除非该排列已经是最大的排列。
我们希望找到一种方法,能够找到一个大于当前序列的新序列,且变大的幅度尽可能小。具体地:
我们需要将一个左边的「较小数」与一个右边的「较大数」交换,以能够让当前排列变大,从而得到下一个排列。
同时我们要让这个「较小数」尽量靠右,而「较大数」尽可能小。当交换完成后,「较大数」右边的数需要按照升序重新排列。这样可以在保证新排列大于原来排列的情况下,使变大的幅度尽可能小。
class Solution {
public void nextPermutation(int[] nums) {
int i=nums.length-2;//从该下标开始
while(i>=0&&nums[i]>=nums[i+1]){
//只有遇到比最后一个数字小的数字才能弹出
//否则就一直向前
//此时就是第一次扫描
//寻找非降序的a[i-1]
i--;
}
// if(i>=0){
// //第二次扫描
// //扫描下标i之后
// //找到比寻找的a[i-1]大的数字
// int tmp=nums.length-1;//要找到比此下标大的数,在一定范围内
// int j;
// for(j=nums.length-1;j>i;j--){
// if(nums[j]<nums[i]){
// tmp=j;//更新下标
// break;
// }
// }
// swap(nums,i,tmp);
// }
if (i >= 0) {
int j = nums.length - 1;
while (j >i && nums[i] >= nums[j]) {
j--;
}
swap(nums, i, j);
}
reverse(nums,i+1);//更新后续
}
public void swap(int[] nums, int i, int j) {
int temp = nums[i];
nums[i] = nums[j];
nums[j] = temp;
}
public void reverse(int[] nums, int start) {
int left = start, right = nums.length - 1;
while (left < right) {
swap(nums, left, right);
left++;
right--;
}
}
}2.搜索旋转排序数组
33. 搜索旋转排序数组 - 力扣(LeetCode)
整数数组
nums按升序排列,数组中的值 互不相同 。在传递给函数之前,
nums在预先未知的某个下标k(0 <= k < nums.length)上进行了 旋转,使数组变为[nums[k], nums[k+1], ..., nums[n-1], nums[0], nums[1], ..., nums[k-1]](下标 从 0 开始 计数)。例如,[0,1,2,4,5,6,7]在下标3处经旋转后可能变为[4,5,6,7,0,1,2]。给你 旋转后 的数组
nums和一个整数target,如果nums中存在这个目标值target,则返回它的下标,否则返回-1。你必须设计一个时间复杂度为
O(log n)的算法解决此问题。
方法一:二分查找
对于有序数组,可以使用二分查找的方法查找元素。
进行旋转后只保证了数组的局部是有序的,这还能进行二分查找吗?答案是可以的。
始终有一侧是有序的
我们可以通过画图知道某一侧有序的特征!!!
class Solution {
public int search(int[] nums, int target) {
int n = nums.length;
if (n == 0) {
return -1;
}
if (n == 1) {
return nums[0] == target ? 0 : -1;
}
// 上面是两种特殊情况
int l = 0;
int r = n - 1;
while (l <= r) {
int mid = (l + r) / 2;
if (nums[mid] == target) {
return mid;
}
if (nums[0] <= nums[mid]) {
// 这个判断的就是左侧是有序的情况
// 此时需要判断左部分是不是有序的
// 判断是不是在该区间内
//区间left,right范围内必须是闭的
if (nums[0] <= target && target <nums[mid]) {
r = mid - 1;
} else {
l = mid + 1;
}
} else {// 开始判断右侧是有序的情况
if (nums[mid] < target && target <= nums[n - 1]) {
l = mid + 1;
} else {
r = mid - 1;
}
}
}
return -1;
}
}3.在排序数组中查找元素的第一个和最后一个位置
34. 在排序数组中查找元素的第一个和最后一个位置 - 力扣(LeetCode)
给你一个按照非递减顺序排列的整数数组
nums,和一个目标值target。请你找出给定目标值在数组中的开始位置和结束位置。如果数组中不存在目标值
target,返回[-1, -1]。你必须设计并实现时间复杂度为
O(log n)的算法解决此问题。
//看到该时间复杂度我想到了用二分法解决该问题
方法一:二分法
class Solution {
public int[] searchRange(int[] nums, int target) {
//首先进行特殊情况的处理
if(nums.length==0){
return new int[]{-1,-1};
}
if(nums.length==1){
return nums[0]==target?new int[]{0,0}:new int[]{-1,-1};
}
int l=0,r=nums.length-1;
while(l<=r){
int mid=(l+r)/2;
if(nums[mid]==target){
l=r=mid;
//找到左标记
while(l>=1&&nums[l-1]==target){
l--;
}
//找到右标记
while(r<nums.length-1&&nums[r+1]==target){
r++;
}
return new int[]{l,r};
}
if(nums[mid]>target){
r=mid-1;
}else{
l=mid+1;
}
}
return new int[]{-1,-1};
}
}
4.搜索插入位置
35. 搜索插入位置 - 力扣(LeetCode)
给定一个排序数组和一个目标值,在数组中找到目标值,并返回其索引。如果目标值不存在于数组中,返回它将会被按顺序插入的位置。
请必须使用时间复杂度为
O(log n)的算法。
class Solution {
public int searchInsert(int[] nums, int target) {
//首先进行特殊情况的处理
if(nums.length==0){
return 0;
}
// if(nums.length==1){
// return nums[0]==target?0:-1;
// }
int l=0,r=nums.length-1;
int ans=nums.length;
while(l<=r){
int mid=(l+r)/2;
if(nums[mid]==target){
return mid;
}
if(nums[mid]>=target){
ans=mid;
r=mid-1;
}else{
l=mid+1;
}
}
return ans;
}
}5.有效的数独
请你判断一个
9 x 9的数独是否有效。只需要 根据以下规则 ,验证已经填入的数字是否有效即可。
- 数字
1-9在每一行只能出现一次。- 数字
1-9在每一列只能出现一次。- 数字
1-9在每一个以粗实线分隔的3x3宫内只能出现一次。(请参考示例图)
只能想到暴力求解的方法
力扣的方法
方法一:一次遍历
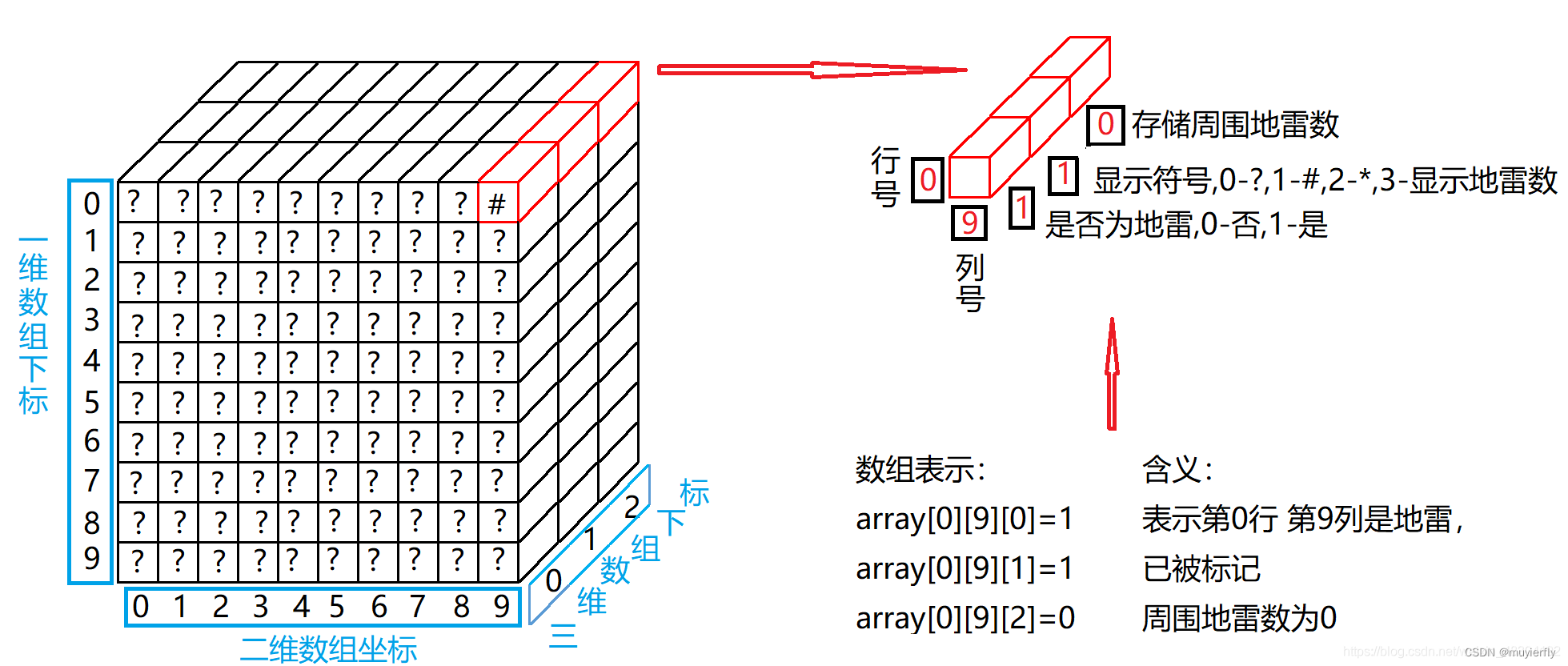
三维数组的图形理解
class Solution {
public boolean isValidSudoku(char[][] board) {
//记录每一行每个数字出现的次数
int[][] rows=new int[9][9];//9个数字每一行出现的次数,纵坐标代表数字几
//记录每一列每个数字出现的次数
int[][] columns=new int[9][9];
//记录每一个小九宫格中每个数字出现的次数
int[][][] subboxes=new int[3][3][9];
for(int i=0;i<9;i++){
for(int j=0;j<9;j++){
char c=board[i][j];
if(c!='.'){
int index=c-'0'-1;//转为数组,化为相应的下标
rows[i][index]++;
columns[j][index]++;
subboxes[i/3][j/3][index]++;
if(rows[i][index]>1||columns[j][index]>1||subboxes[i/3][j/3][index]>1){
return false;
}
}
}
}
return true;
}
}