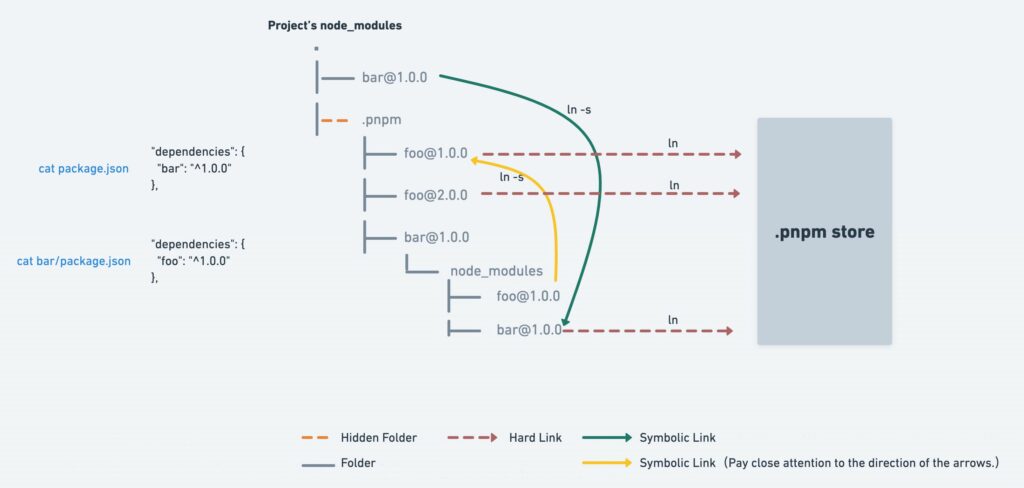
在高精度伺服控制中，前馈控制可用来提高系统的跟踪性能。经典控制理论中的前馈控制设计是基于复合控制思想，当闭环系统为连续系统时，使前馈环节与闭环系统的传递函数之积为1，从而实现输出完全复现输入。利用前馈控制的思想，针对PID控制设计了前馈补偿，以提高系统的跟踪性能,其结构如图1所示。

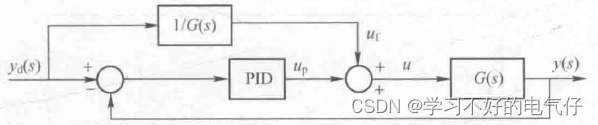
图1 PID前馈控制结构

仿真实例：

被控对象为：

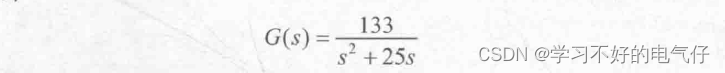
输入信号为yd(k)=0.5sin(6Tt)，采样时间为1ms。

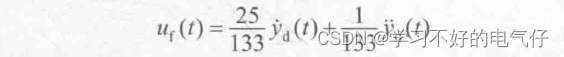
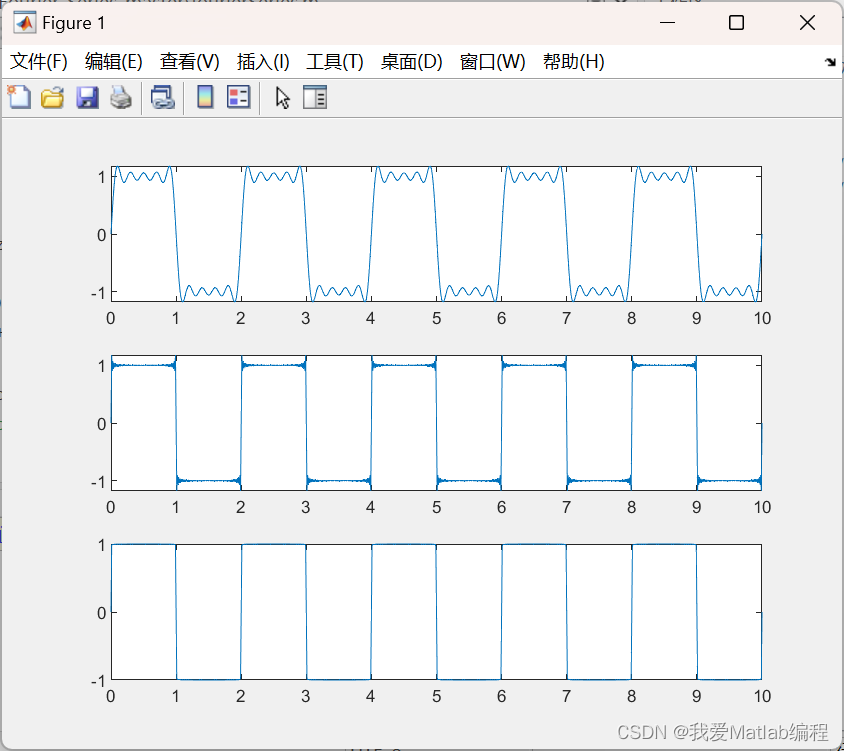
只采用PID正弦跟踪控制方法的结果如图2所示。采用前馈PID控制方法的跟踪结果如图3所示。可见通过前馈补偿可大大提高系统的跟踪性能。

本方法的不足之处是需要被控对象的精确模型。

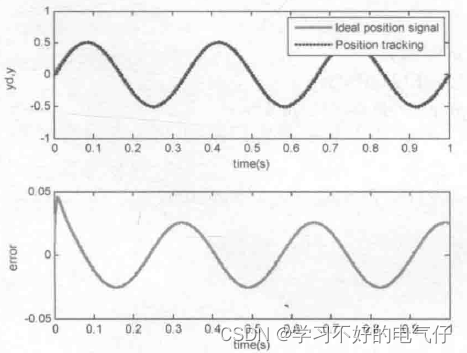
图1 PID正弦跟踪及跟踪误差（M=1）

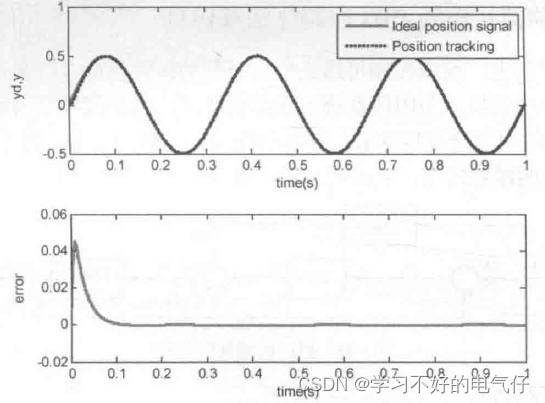
图2 PID+前馈补偿正弦跟踪及跟踪误差（M=2）

仿真程序：

clear all;close all;

ts=0.001;

sys=tf(133,[1,25,0]);

dsys=c2d(sys,ts,Z);

[num,den]=tfdata(dsys,'v);

u_1=0;u_2=0;

y_1=0;y_2=0;

error_1=0;ei=0;

for k=1:1:1000

time(k)=k*ts;

A=0.5;F=3.0;

yd(k)=A*sin(F*2*pi*k*ts);

dyd(k)=A*F*2*pi*cos(F*2*pi*k*ts);

ddyd(k)=-A*F*2*pi*F*2*pi*sin(F*2*pi*k*ts);

%Linear model

y(k)=-den(2)*y1-den(3)*y_2+num(2)*u_1+num(3)*u_2;

error(k)=yd(k)-y(k);

ei=eiterror(k)*ts;

up(k)=80*error(k)+20*ei+2.0*(error(k)-error_1)/ts;

uf(k)=25/133*dyd(k)+1/133*ddyd(k);

M=2;

if M==1

%Only using PID

u(k)=up(k);

elseif M==2 %PID+Feedforward

u(k)=up(k)+uf(k);

end

if u(k)>=10

u(k=10;end

ifu(k)<--10

u(k=-10;end

u_2=u_1;u_1=u(k);y_2=y_1;y_1=y(k);error_1=error(k);

end

figure(1);subplot(211);

plot(time,yd,'r,time,y,'k:' linewidth',2);xlabel('time(s)');ylabel('yd,y');

legend('ldeal position signal' 'Position tracking):subplot(212);

plot(time,error,'r,'linewidth',2);xlabel('time(s)';ylabel('error');figure(2);

plot(time,up,'k', timeuf,'b',time,u.'r'linewidth1,2);xlabel('time(s)');ylabel('up,uf,u');