本篇文章主要回顾一下几年前学的JPS跳点搜索规划算法的相关内容,之前学的时候没有进行概括总结,现在补上

一、A*算法简单回顾
–
1、基本介绍和原理
A*(A-Star)算法是一种静态路网中求解最短路径最有效的直接搜索方法,也是解决许多搜索问题的有效算法。
其代价函数表示为: f(n)=g(n)+h(n),其中 f(n) 是从初始状态经由状态n到目标状态的代价估计,g(n) 是在状态空间中从初始状态到状态n的实际代价,h(n) 是从状态n到目标状态的最佳路径的估计代价。(对于路径搜索问题,状态就是图中的节点,代价就是距离)
h(n)的选取:保证找到最短路径(最优解的)条件,关键在于估价函数f(n)的选取(或者说h(n)的选取)。我们以d(n)表达状态n到目标状态的距离,那么h(n)的选取大致有如下三种情况:
(1)如果h(n)< d(n)到目标状态的实际距离,这种情况下,搜索的点数多,搜索范围大,效率低。但能得到最优解。
(2)如果h(n)=d(n),即距离估计h(n)等于最短距离,那么搜索将严格沿着最短路径进行, 此时的搜索效率是最高的。
(3)如果 h(n)>d(n),搜索的点数少,搜索范围小,效率高,但不能保证得到最优解。
在一个极端情况下,如果h(n)为0,则只g(n)起作用,A*变成Dijkstra算法,保证找到最短路径。
在另一个极端,如果h(n)相对于 非常高g(n),则仅h(n)起作用,并且 A* 变成贪婪的最佳优先搜索。
–
2、算法流程
① 将初始节点放入到open列表中。
②检查当前open列表。如果为空,则搜索失败,停止循环。如果open列表中存在目标节点,则搜索成功,停止循环。不属于以上两种情况,则继续循环。
③从open列表中取出F值最小的节点作为当前节点,并将其加入到close列表中。
④ 计算当前节点的相邻的所有可到达节点,生成一组子节点。对于每一个子节点:
如果该节点在close列表中,则丢弃它
如果该节点在open列表中,则检查其通过当前节点计算得到的F值是否更小,如果更小则更新其F值,并将其父节点设置为当前节点。
如果该节点不在open列表中,则将其加入到open列表,并计算F值,设置其父节点为当前节点。
⑤ 本轮扩展结束, 转到第②步,循环进行下一轮扩展。
3、A*算法的详细介绍
Amit’s A* Pages【点击可跳转】

二、JPS算法简介
JPS(Jump Point Search)跳点搜索是一种高效的路径规划算法,用于在网格地图上找到两点之间的最短路径。它是A*算法的一种改进,通过利用地图的拓扑结构,在搜索过程中跳过某些不必要的节点,从而减少搜索的时间和空间复杂度。
1. 基本思想
JPS利用了网格地图的拓扑结构,通过计算出地图中节点的“跳跃点”(jump points),以及与这些跳跃点相邻的“强制邻居”(forced neighbors)。在搜索过程中,JPS会按照预先确定的跳跃点和强制邻居的规则,跳跃式地搜索直到找到目标点或者无法继续跳跃。
2. 搜索过程
JPS搜索过程类似于A*算法,但是在搜索的过程中会跳跃式地前进,而不是逐个节点地扩展。在每个节点处,JPS会检查并记录可到达的跳跃点和强制邻居,然后根据这些信息继续搜索。如果发现了目标点,或者无法再进行跳跃,则搜索结束。
3. 优点
JPS通过跳跃式搜索,减少了搜索空间和搜索时间,尤其在大规模地图上效果显著。由于JPS只考虑特定的跳跃点和强制邻居,因此避免了对不必要的节点进行扩展,提高了搜索效率。
4. 缺点
JPS算法对于非网格地图(如连续空间)并不适用,因为它依赖于网格地图的拓扑结构。

–
三、JPS算法的扩展策略(核心)
JPS算法与A*算法的最大不同在于其更加高效的扩展策略,具体分为横向和纵向扩展、对角扩展两种情况。
首先来介绍,相对简单的横向和纵向扩展情况。
1、横向和纵向扩展策略
横向扩展和纵向扩展策略是相同的,这里以横向扩展为例进行介绍,假设从下面左图中的绿色栅格水平向右进行搜索,对于其邻居可以做以下分析和假设。首先,我们可以忽略其左边的邻居栅格,如下面右图中的灰色栅格所示,因为,按照水平向右到的搜索方向,在访问当前绿色节点之前,该灰色节点已经被访问过了,因此,忽略它。
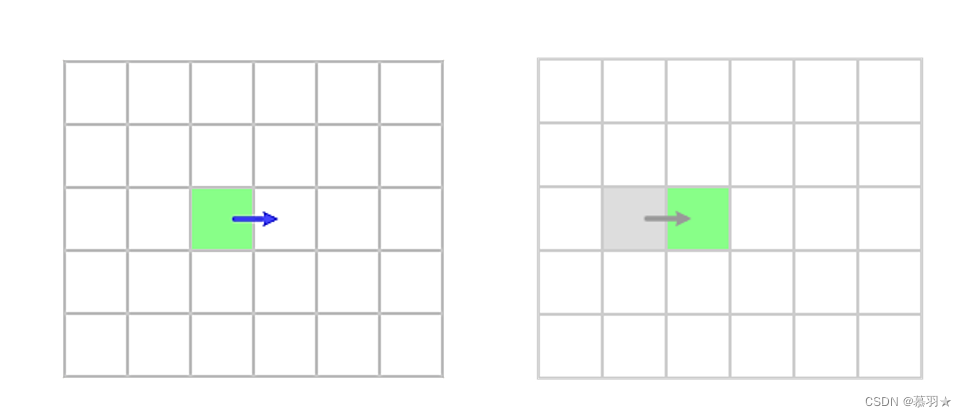
其次,我们同样可以忽略下面两幅图中的标号为②~⑤的邻居栅格,因为通过之前访问过的栅格①,到达栅格②和③的成本为栅格①的现有成本+1 (假设栅格边长为1),而如果通过当前的绿色栅格到达栅格②和③的成本为栅格①的现有成本+1 + 根号2,显然成本高于由栅格①直接到达栅格②和③的成本。所以可以直接忽略邻居节点②和③,同理,对于栅格④和⑤,由栅格①到达的成本为栅格①的现有成本+根号2,而由绿色栅格到达的成本为栅格①的现有成本+2,所以邻居栅格④和⑤同样可以忽略。
即下图中的邻居栅格 ② ~ ⑤,由之前已经访问过的栅格①扩展,比由当前的绿色栅格扩展成本更低,所以在进行绿色栅格扩展时,完全可以忽略对这些邻居节点的扩展。
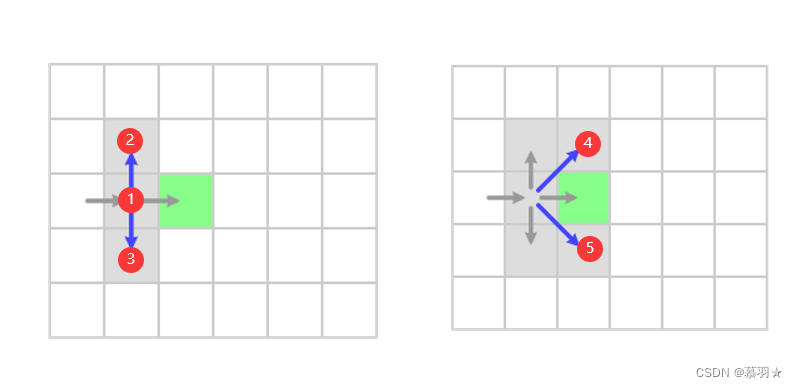
然后,对于邻居栅格⑥和⑦,通过之前访问过的栅格①途径绿色栅格到达或途径灰色栅格到达的成本是一样的,比如对于栅格⑥,①→④→⑥和①→绿色栅格→⑥的成本都是栅格①的现有成本+1+根号2,所以为了简单起见,我们同样假设可以不通过绿色栅格到达,因此栅格⑥和⑦也可以忽略。
至此,绿色栅格的邻居栅格就只剩下了其右侧的栅格⑧,如下面中间的图所示,也就是说,在没有障碍物的情况下,JPS的横向和纵向扩展仅需要考虑其扩展方向上的下一个栅格即可,而无需考虑其他相邻点,对于这里介绍的例子,即可以不断的向右搜索下去,如下面的右图所示。
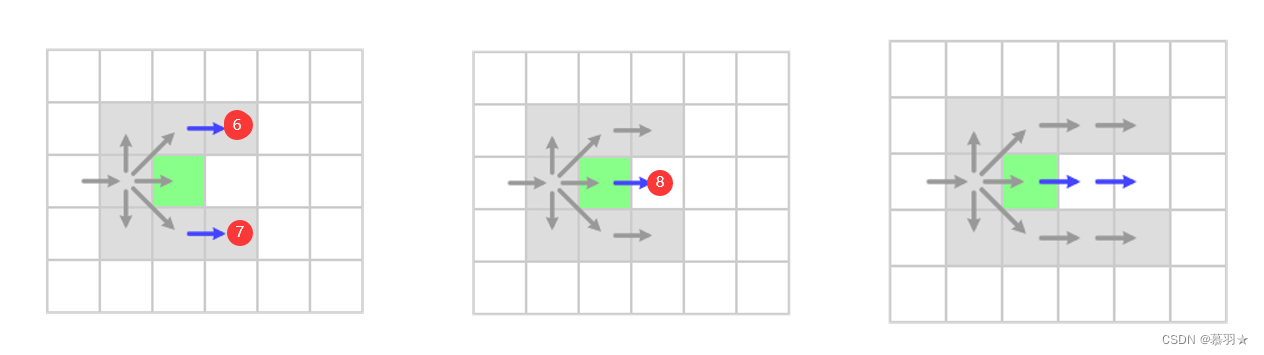
那么什么情况下需要停止呢? 添加到open列表中的待选扩展点又应该如何选?
若在不断的向右搜索下去的过程中,当前栅格的上方或者下方存在障碍物时,就必须要停止下来了,如下面的左图所示,因为,此时由于绿色栅格上方的邻居点为障碍物,此时,紫色的栅格无法再通过前面介绍的①→④→⑥路径到达,只能通过①→绿色栅格→⑥的方式到达,此时紫色栅格就不能被忽略,其被称为强制邻居,因此,我们必须停止一味的向右探索的形式,终止探索,并将当前的绿色栅格作为新的待选扩展点,添加到open列表中,并将紫色的栅格添加到绿色栅格的强制邻居列表中。
也就是说,当我们沿着横向或者纵向探索到达具有强制邻居的栅格时,我们停止跳跃(本例中即为停止向右跳跃),并将当前栅格添加到开放集open中以供稍后进一步检查和扩展。
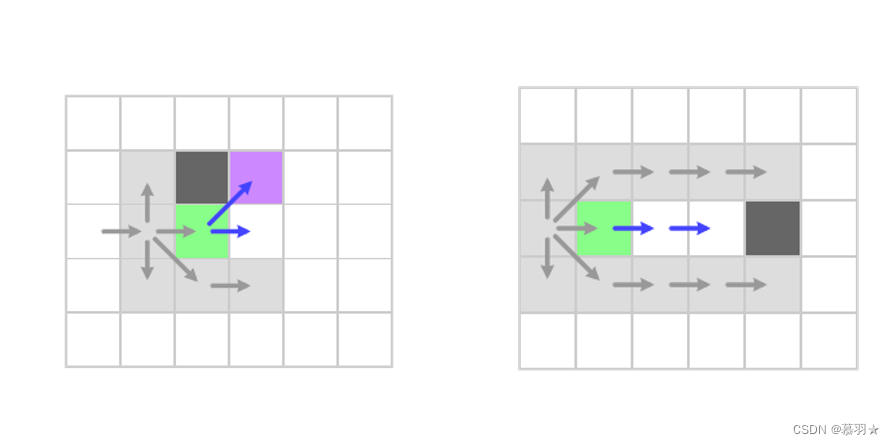
除了上面介绍的遇到具有强制邻居的栅格之外,如果我们向右跳跃时道路被挡住,即遇到了障碍物或者到达了地图边界,如上面的右图所示,我们可以放心地停止和忽略整个跳跃。因为,我们已经假设上方和下方的路径是通过其他栅格处理的,若没有遇到具有强制邻近的栅格,且朝右侧探索到了地图边界或者被障碍物挡住了,即没有必要朝和这个方向进行探索尝试了,直接忽略整个跳跃,也就是不需要向open列表中添加任何新的待扩展点。
2、对角扩展策略
与横向扩展和纵向扩展类似,对于当前栅格,即下图中的绿色栅格,其邻居栅格①是之前访问过的栅格,可以直接忽略,由①不经过绿色栅格到达②~⑤的成本低于经过绿色栅格的情况,因此邻居栅格②到⑤也可以被忽略。
与横向扩展和纵向扩展不同的是,尽管经过和不经过绿色栅格到达⑥或⑦的成本是相同的,在对角扩展中并不会忽略通过绿色栅格到达的情况,也就是说对角扩展中需要考虑三个方向的邻居栅格,本例中即为⑥到⑧,如下面的左图所示,与横向或者纵向扩展类似,当邻居栅格②或③处存在障碍物时,此时无法再通过②或③到达④或⑤,因此不能被忽略,此时对应的④或⑤成为强制邻居,如下面右图中的紫色栅格所示。
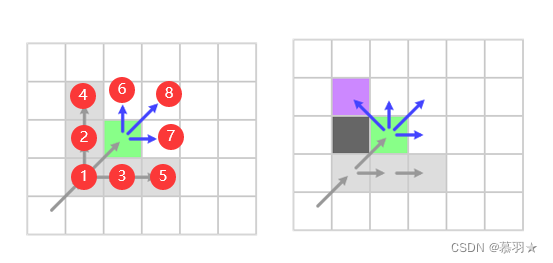
对角扩展中存在三个扩展方向,那么以什么形式进行扩展(跳跃)呢?
对角扩展的形式为,对于横向和纵向运动的⑥和⑦直接按照上面介绍的独立横向和纵向扩展策略进行扩展。对于对角方向的扩展,采用沿着对角方向移动一步后,在新位置⑧处调用横向和纵向扩展的策略进行扩展,如果这两个方向上都没有找到可以新加入到open列表中的带扩展点,则继续沿着当前对角方向,再移动一步,在新位置处继续调用横向和纵向扩展的策略进行扩展… ,直至在对角方向遇到障碍物或者到达边界,返回,并忽略该方向的扩展。或者在调用横向或纵向扩展过程中遇到了具有强制邻居的节点,则将此时调用横向或纵向节点的位置处作为新的扩展点,加入到open列表中,并停止对角方向的扩展。
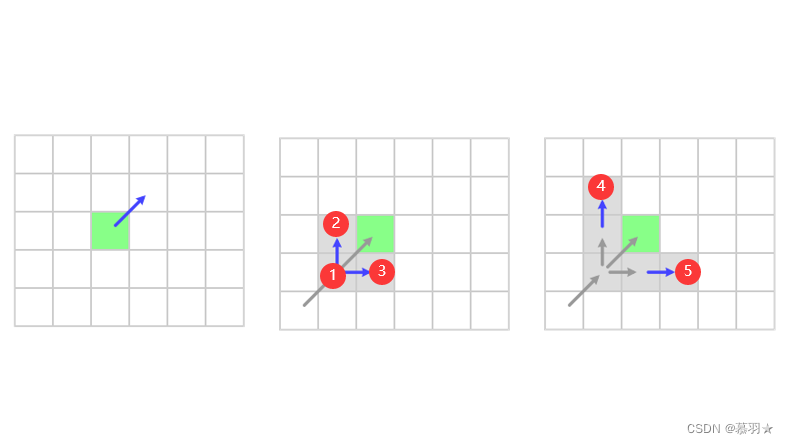
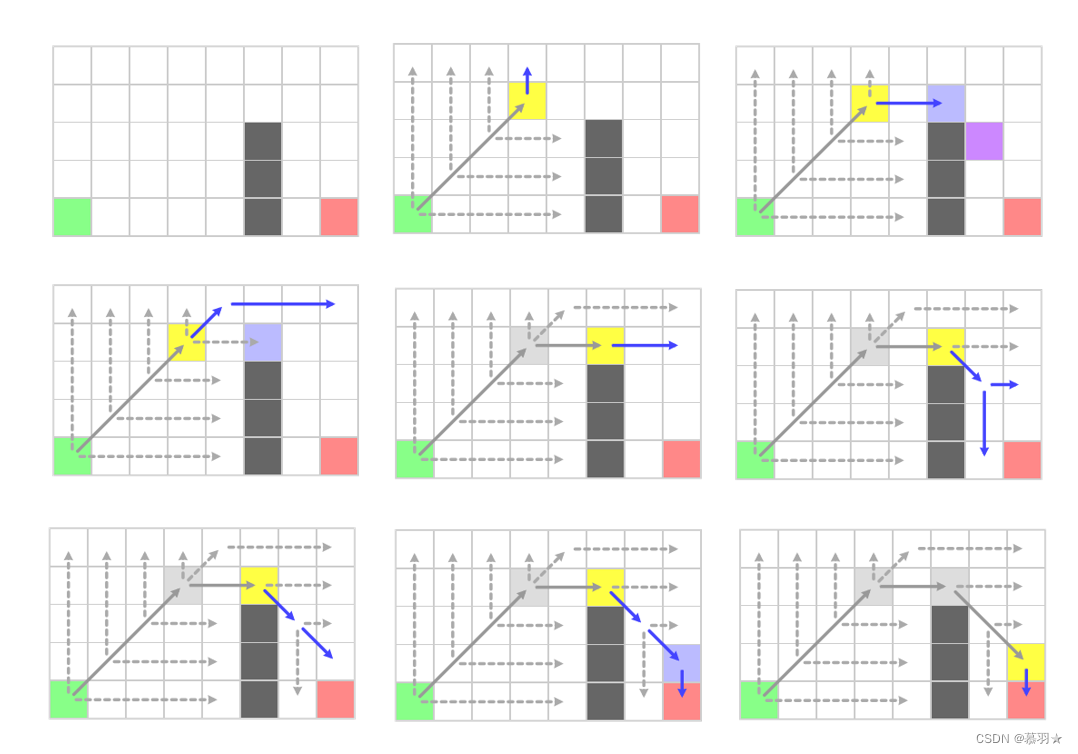
下面看一个具体示例,在当前栅格处(即下图中的绿色栅格)进行对角扩展,如下面的图一所示,在独立的横向扩展中出现了右侧栅格为障碍物的情况,也没有发现具有强制邻居的点,直接忽略,同样在独立的纵向扩展中到达了地图边界也没有具有强制邻居的点,直接忽略。对于对角方向的扩展,沿着对角方向移动一步,到达①处,然后在①处调用横向和纵向扩展,如图二所示,没有具有价值的点,继续沿着对角方向走一步,到达②处,然后继续在②处进行横向和纵向扩展,如图三所示,同样没有具有价值的点,继续沿着对角方向走一步,到达③处。
在③处进行横向扩展时,发现了具有强制邻居的点④,如图四所示,此时对角扩展结束,将栅格③作为新发现的带扩展点添加到open列表中,注意添加的是③而不是④,如图五所示。此时就可以进行按照与A*算法类似的流程进行下一轮迭代了。

这里有一点要强调,这里说的对角扩展策略其实包含横向、纵向、和对角扩展三个方向的,当然对角扩展里面又调用了横向和纵向扩展。这三个方向扩展的停止是独立的,比如下图中的①处,其父节点为绿色栅格所示的起点,可知在进行①处节点扩展时,其扩展方向为右上的对角方向,此时需要进行横向、纵向、对角三个方向的扩展,对于横向扩展而言,没有遇到具有强制邻居的点,就在右侧出现了障碍物,停止并忽略整个横向扩展。对于纵向扩展,发现了具有强制邻居的节点②,将②加入到open列表中,并停止纵向扩展。 虽然在纵向扩展中已经找到了一个具有强制邻居的点,并加入了open中,但其发生在①处独立的横向和纵向扩展过程中,而非对角扩展调用了横向和纵向扩展,所以对于对角扩展要继续进行,直至在④处调用横向扩展时,发现了具有强制邻居的节点③,此时对角扩展才结束,并将④加入到open列表中。
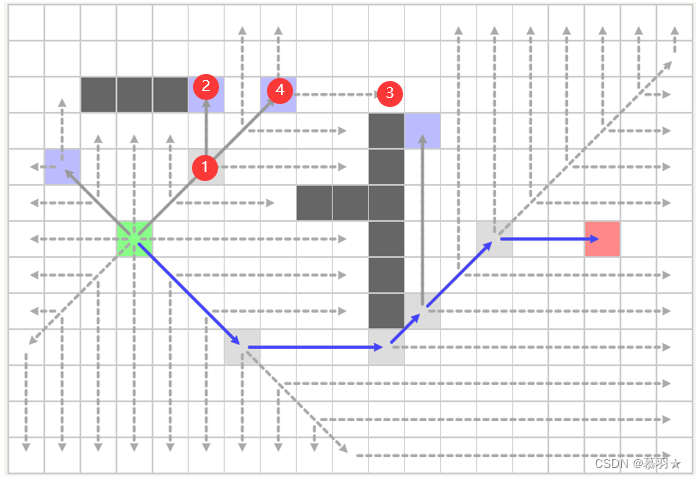
总结一下什么样的点可以作为添加到open列表中,作为待拓展点,或者说跳点?
情况1:该节点为起点或终点,如上图中的绿色和红色栅格所示。
情况2:该节点存在强制邻居节点,如上图中的②。【该情况常发生于独立的横向或纵向扩展中,伴随着独立的横向或纵向扩展停止,而非对角扩展调用的横向和纵向扩展】
情况3:该节点的父节点通过对角移动到该节点,且该节点的横向或纵向上存在具有强制邻居的点,如上图中的①和④所示。【该情况常发生于对角扩展调用的横向和纵向扩展中,伴随着对角扩展停止】
四、JPS算法的流程
除了扩展策略外,JPS算法流程与A * 算法类似,如下所示:
① 将初始节点放入到open列表中。
②检查当前open列表。如果为空,则搜索失败,停止循环。如果open列表中存在目标节点,则搜索成功,停止循环。不属于以上两种情况,则继续循环。
③从open列表中取出F值最小的节点作为当前节点,并将其加入到close列表中。
④ 根据当前节点的父节点,确定由其父节点到当前节点的运动方向,来确定采用横向和纵向扩展策略还是采用对角扩展策略,进行当前点的扩展,此外,如果当前节点的强制邻居列表不为空,即当前节点存在强制邻居节点,强制邻居节点所在方向也需要进行扩展。特别的,对于起点没有父节点,需要对八个方向都进行探索。
当然,对于上述过程中得到准备放入open列表中的待扩展点,跟A * 算法类似,同样对其进行检查:
如果该节点在close列表中,则丢弃它
如果该节点在open列表中,则检查其通过当前节点计算得到的F值是否更小,如果更小则更新其F值,并将其父节点设置为当前节点。
如果该节点不在open列表中,则将其加入到open列表,并计算F值,设置其父节点为当前节点。
⑤ 本轮扩展结束, 转到第②步,循环进行下一轮扩展。
一个执行示例如下所示:
得到的可行路径如下:
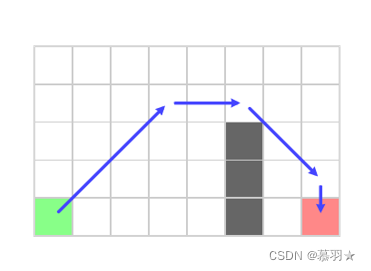
具体的详细的按步讲解的示例可见参考资料2所列的博客所示
五、在线交互式可视化资源
1、https://qiao.github.io/PathFinding.js/visual/
2、https://zerowidth.com/2013/a-visual-explanation-of-jump-point-search/


参考资料
1、A Visual Explanation of Jump Point Search
2、JPS(jump point search)寻路算法


![mysql [Err] 1118 - Row size too large (> 8126).](https://img-blog.csdnimg.cn/direct/73f4b506550f4a619afcf0a24966ac02.png)