1、原理及流程
深度学习的线性预测是一种利用深度神经网络模型进行线性回归预测的方法。其设计原理主要基于神经网络的层次化特性,利用多层感知器(MLP)等模型进行特征学习和非线性变换,从而提高线性预测的准确性。
设计流程如下:
-
数据准备:准备带有标签的训练数据集,包括输入特征和对应的输出标签。
-
特征提取:对输入特征进行特征提取和预处理,包括标准化、归一化等操作。
-
构建神经网络:设计一个包含多个隐藏层的深度神经网络模型,其中每个隐藏层使用非线性激活函数(如ReLU)进行变换。最后一层输出层使用线性激活函数(如线性激活函数)进行线性回归预测。
-
训练模型:使用训练数据集对神经网络模型进行训练,采用梯度下降等优化算法不断更新模型参数,使模型输出尽可能接近真实标签。
-
模型评估:使用验证集对训练好的神经网络模型进行评估,计算模型的准确率、损失函数等指标。
-
模型优化:根据评估结果对模型进行优化和调参,包括调整网络结构、参数初始化、正则化等方法。
-
预测结果:使用训练好的神经网络模型对新数据进行线性回归预测,得到预测结果。
通过以上流程,可以设计一个基于深度学习的线性预测模型,用于处理线性关系复杂或非线性关系较强的预测问题。
2、线性预测设计说明
说明:设计线性神经元来预测给定最后五个值的时间序列中的下一个值。
1)设计神经网络需要考虑的问题
当设计神经网络时,通常需要考虑以下问题:
-
网络结构:确定神经网络的层数、每层的神经元数量和连接方式,以及选择合适的激活函数。
-
损失函数:选择适当的损失函数来度量模型输出与真实标签之间的差距,例如均方误差(MSE)用于回归问题,交叉熵用于分类问题。
-
优化算法:选择合适的优化算法来更新网络参数,如随机梯度下降(SGD)、动量法(Momentum)、Adam等。
-
学习率:调整学习率的大小,以控制参数更新的步长,防止模型过拟合或欠拟合。
-
正则化:通过添加正则化项(如L1正则化、L2正则化)来防止过拟合。
-
批量大小:确定每次迭代训练时的批量大小,同时平衡训练速度和模型性能。
-
参数初始化:选择合适的参数初始化方法,如随机初始化、Xavier初始化等,有助于加速训练收敛。
-
超参数调优:调节网络结构、损失函数、优化算法等超参数,以优化模型性能。
-
验证与测试:使用验证集对模型进行验证,避免过拟合;最终通过测试集评估模型的性能。
-
超参数搜索:可以使用网格搜索、随机搜索或贝叶斯优化等方法来搜索最佳的超参数组合。
考虑以上问题,可以更好地设计和调整神经网络模型,提高模型的性能和泛化能力。
3、定义波形(正弦波)
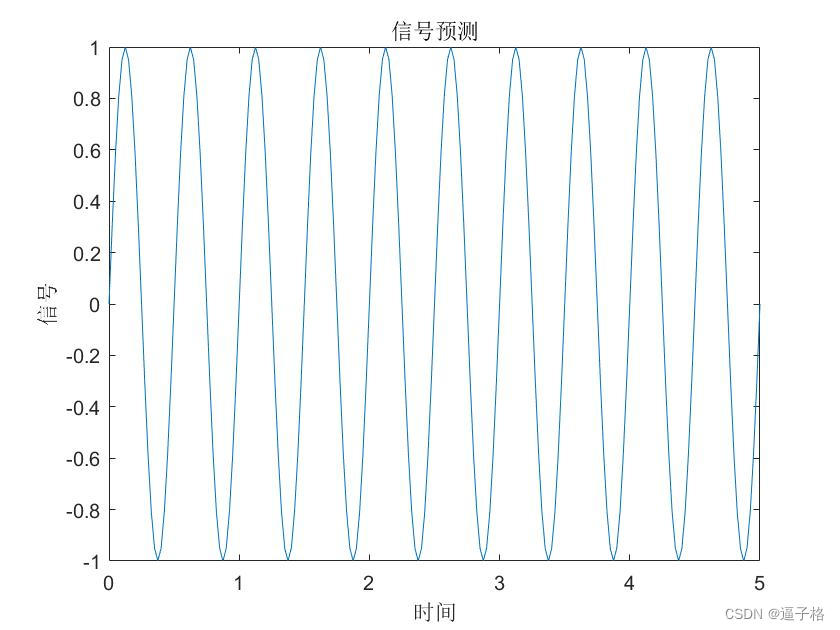
说明:时间定义为 0 到 5 秒,步长为 1/40 秒,信号为正弦波
代码
time = 0:0.025:5;
signal = sin(time*4*pi);
plot(time,signal)
figure(1)
xlabel('时间');
ylabel('信号');
title('信号预测');效果图
4、为神经网络设置问题(信号转换为元胞数组)
说明:然后将信号转换为元胞数组。神经网络将时间步表示为一个元胞数组的各列,并将它们与在给定时间的不同样本区分开来,后者用矩阵列表示。
代码
signal = con2seq(signal);
Xi = signal(1:4);%前四个值作为初始输入延迟状态
X = signal(5:(end-1));%其余的值作为输入
timex = time(5:(end-1));
T = signal(6:end);%目标定义为匹配输入,前移一个时间步。5、设计线性层
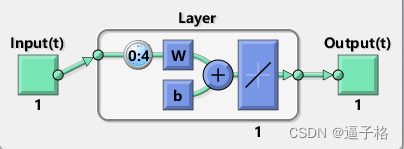
说明:函数 newlind 现在将设计具有单个神经元的线性层,该层在给定当前值和四个过去值的情况下预测信号的下一个时间步。
代码
net = newlind(X,T,Xi);%设计具有单个神经元的线性层,该层在给定当前值和四个过去值的情况下预测信号的下一个时间步。
view(net)视图效果
6、测试线性层
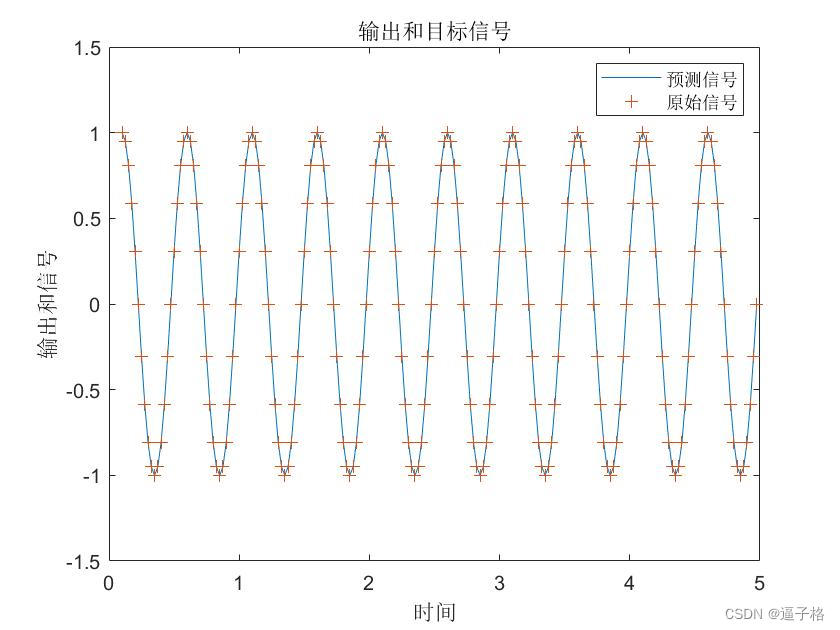
说明:对输入和延迟状态调用网络(就像调用函数一样),以获得它的时间响应。
绘制输出信号与目标代码
Y = net(X,Xi);
%绘制输出信号与目标。
figure(2)
plot(timex,cell2mat(Y),timex,cell2mat(T),'+')
xlabel('时间');
ylabel('输出和信号');
title('输出和目标信号');
legend('预测信号','原始信号')视图效果
绘制误差代码
figure(3)
E = cell2mat(T)-cell2mat(Y);
plot(timex,E,'r')
xlabel('时间');
ylabel('误差');
title('误差信号');视图效果

7、总结
在MATLAB中基于深度学习的线性预测设计通常涉及以下步骤:
数据准备:首先需要准备带有标签的训练数据集和测试数据集,并对数据进行必要的预处理和特征提取,如归一化、标准化等操作。
1网络设计:使用MATLAB中的深度学习工具箱(Deep Learning Toolbox)构建一个包含多个隐藏层的深度神经网络模型,可以选择使用全连接神经网络或者其他类型的网络结构。
2模型训练:通过调用MATLAB中的训练函数(如trainNetwork)对构建的神经网络模型进行训练,指定适当的优化算法和损失函数,同时注意调节超参数以获得更好的性能。
net = feedforwardnet(hiddenLayerSize); % 创建一个全连接的前馈神经网络
net.trainFcn = 'trainlm'; % 指定使用Levenberg-Marquardt优化算法来训练网络
net = train(net, X_train, Y_train); % 对训练数据集进行训练3模型评估:使用测试数据集对训练好的神经网络模型进行评估,计算模型的准确率、均方误差等指标,可以调用MATLAB中的evaluate函数来实现。
Y_pred = net(X_test); % 使用训练好的网络模型进行预测
mse = mean((Y_pred - Y_test).^2); % 计算均方误差4模型优化:根据评估结果对模型进行优化和调参,包括调整网络结构、学习率、正则化参数等超参数。
5预测结果:最后,使用训练好的神经网络模型对新数据进行线性预测,得到预测结果。
通过以上步骤,可以在MATLAB环境中实现基于深度学习的线性预测模型的设计和训练。
8、源代码
%% 线性预测设计
%设计线性神经元来预测给定最后五个值的时间序列中的下一个值。
%% 定义波形(正弦波)
time = 0:0.025:5;
signal = sin(time*4*pi);
plot(time,signal)
figure(1)
xlabel('时间');
ylabel('信号');
title('信号预测');
%% 为神经网络设置问题(信号转换为元胞数组)
signal = con2seq(signal);
Xi = signal(1:4);%前四个值作为初始输入延迟状态
X = signal(5:(end-1));%其余的值作为输入
timex = time(5:(end-1));
T = signal(6:end);%目标定义为匹配输入,前移一个时间步。
%% 设计线性层
net = newlind(X,T,Xi);%设计具有单个神经元的线性层,该层在给定当前值和四个过去值的情况下预测信号的下一个时间步。
view(net)
%% 测试线性层
%对输入和延迟状态调用网络,获得它的时间响应。
Y = net(X,Xi);
%绘制输出信号与目标。
figure(2)
plot(timex,cell2mat(Y),timex,cell2mat(T),'+')
xlabel('时间');
ylabel('输出和信号');
title('输出和目标信号');
%绘制误差
figure(3)
E = cell2mat(T)-cell2mat(Y);
plot(timex,E,'r')
xlabel('时间');
ylabel('误差');
title('误差信号');