目录
一、使用回归分析方法分析某病毒是否与温度呈线性关系
1.1 代码实现
1.2 线性回归结果
1.3 相关系数验证
二、使用判别分析方法预测某病毒在一定的温度下是否可以存活,分别使用三种判别方法,包括Fish判别、贝叶斯判别、LDA
2.1 数据集展示:实验二2-2.csv
2.2 代码实现
2.3 判别结果
三、使用聚类分析方法分析病毒与温度、湿度的关系
3.1 代码实现
3.2 聚类分析结果
未完待续-----
一、使用回归分析方法分析某病毒是否与温度呈线性关系
数据集:实验三2-1.xls
| T | COUNT |
| 5 | 1000 |
| 10 | 950 |
| 12 | 943 |
| 14 | 923 |
| 20 | 910 |
| 21 | 900 |
| 25 | 889 |
| 27 | 879 |
| 30 | 870 |
| 32 | 832 |
| 33 | 827 |
| 35 | 801 |
| 38 | 783 |
| 40 | 620 |
采用线性回归分析方法
1.1 代码实现
import pandas as pd
from sklearn.linear_model import LinearRegression
import matplotlib.pyplot as plt
# 中文字体调整
plt.rcParams['font.family'] = ['Arial Unicode Ms']
# 读取 Excel 文件并创建数据框
file_path = '实验三3-1.xls'
data = pd.read_excel(file_path)
# 定义自变量和因变量
X = data[['T']]
y = data['COUNT']
# 创建并拟合线性回归模型
model = LinearRegression()
model.fit(X, y)
# 获取回归系数和截距
slope = model.coef_[0]
intercept = model.intercept_
# 打印回归方程
print(f"回归方程: 病毒存活数 = {intercept:.2f} + {slope:.2f} * 温度")
# 绘制散点图和回归线
plt.scatter(X, y, color='blue', label='实际数据')
plt.plot(X, model.predict(X), color='red', linewidth=2, label='拟合回归线')
# 主题
plt.title('病毒存活数量与温度的线性关系')
plt.xlabel('温度(℃)') # x 轴标签添加属性和单位
plt.ylabel('病毒存活数量(个)') # y 轴标签添加属性和单位
plt.legend()
plt.show()1.2 线性回归结果
回归方程如下
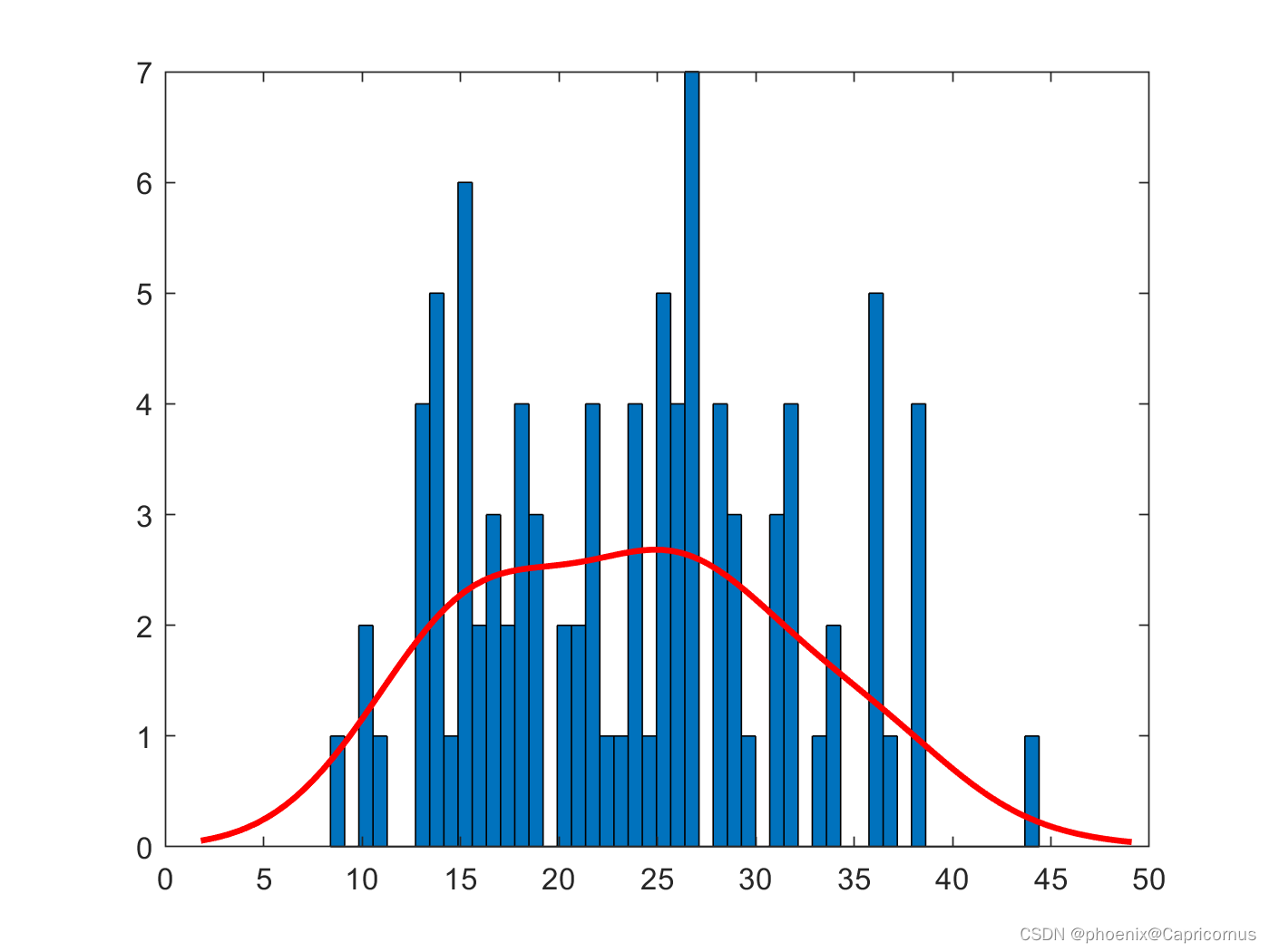
 将线性回归结果绘制成如下图形
将线性回归结果绘制成如下图形
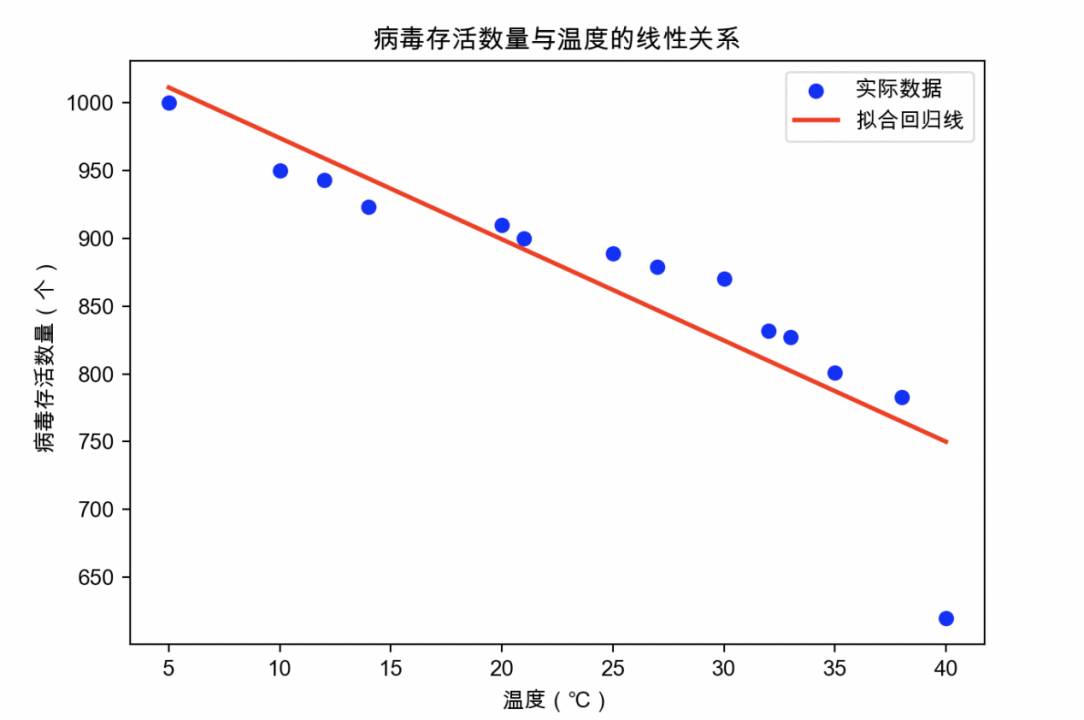
可以看出,除了40摄氏度下的病毒存活数量偏低,其他点都很好的符合回归方程: 病毒存活数 = 1048.50 + -7.46 * 温度。
1.3 相关系数验证
(1)代码如下
import pandas as pd
# 读取 Excel 文件并创建数据框
file_path = '实验三3-1.xls'
data = pd.read_excel(file_path)
# 计算 Pearson 相关系数
pearson_corr = data['T'].corr(data['COUNT'], method='pearson')
# 计算 Spearman 相关系数
spearman_corr = data['T'].corr(data['COUNT'], method='spearman')
print(f"Pearson 相关系数: {pearson_corr:.2f}")
print(f"Spearman 相关系数: {spearman_corr:.2f}")(2)根据数据集计算出的相关系数结果如下

根据计算结果可以得出结论:温度与病毒数量之间呈现出较强的负相关关系。
Pearson相关系数为-0.89,表明温度与病毒数量之间存在着高度负相关关系。即随着温度的升高,病毒数量呈现下降的趋势;反之,温度降低时,病毒数量则可能增加。Spearman相关系数为-1.00,说明温度与病毒数量之间存在着完全的负相关关系,即它们的关系是单调递减的,温度每上升一个单位,病毒数量就会减少一个单位。
综合以上分析,可以得出结论:温度与病毒数量之间呈现出明显的负相关关系,即温度的变化对病毒数量有着显著的影响,通常情况下温度升高会导致病毒数量减少,而温度降低则可能导致病毒数量增加。
二、使用判别分析方法预测某病毒在一定的温度下是否可以存活,分别使用三种判别方法,包括Fish判别、贝叶斯判别、LDA
2.1 数据集展示:实验二2-2.csv
| temperature | humidity | class |
| 5.127 | 74.978 | 1 |
| -9.274 | 96.247 | 1 |
| -21.371 | 79.613 | 1 |
| -37.5 | 85.109 | 1 |
| -51.325 | 69.282 | 1 |
| -52.477 | 80.49 | 0 |
| -39.804 | 71.718 | 1 |
| -30.588 | 60.388 | 1 |
| 1.671 | 69.788 | 1 |
| 13.191 | 78.306 | 1 |
| 38.537 | 60.747 | 1 |
| 52.938 | 65.94 | 1 |
| 53.882 | 73.829 | 0 |
| 23.675 | 60.753 | 1 |
2.2 代码实现
import pandas as pd
from sklearn.discriminant_analysis import LinearDiscriminantAnalysis
from sklearn.naive_bayes import GaussianNB
from sklearn.discriminant_analysis import QuadraticDiscriminantAnalysis
import numpy as np
# 生成包含极端数据的随机数据
np.random.seed(42)
random_temperatures = np.array([-70.0, 45.0, 23.0, 9.0, -50.0, -50.0, 50.0, 36.0, 10.0, 20.0])
random_humidity = np.array([10.0, 98.0, 93.0, 68.0, 5.0, 100.0, 95.0, 80.0, 77.0, 70.0])
new_data = pd.DataFrame({'temperature': random_temperatures, 'humidity': random_humidity})
# 读取 Excel 文件并创建数据框
file_path = '实验三3-2.csv'
data = pd.read_excel(file_path)
df = pd.DataFrame(data)
X = df[['temperature', 'humidity']]
y = df['class']
# Fisher判别
lda = LinearDiscriminantAnalysis()
lda.fit(X, y)
# 贝叶斯判别
nb = GaussianNB()
nb.fit(X, y)
# LDA
qda = QuadraticDiscriminantAnalysis()
qda.fit(X, y)
# 新数据预测
fisher_pred = lda.predict(new_data)
bayes_pred = nb.predict(new_data)
lda_pred = qda.predict(new_data)
# 输出结果
result_map = {0: '不可以存活', 1: '可以存活'}
fisher_pred_label = [result_map[pred] for pred in fisher_pred]
bayes_pred_label = [result_map[pred] for pred in bayes_pred]
lda_pred_label = [result_map[pred] for pred in lda_pred]
output_data = pd.DataFrame({
'temperature': random_temperatures,
'humidity': random_humidity,
'Fisher判别预测结果': fisher_pred_label,
'贝叶斯判别预测结果': bayes_pred_label,
'LDA预测结果': lda_pred_label
})
print("随机生成的10组数据及其三种判别结果:")
print(output_data)2.3 判别结果

三、使用聚类分析方法分析病毒与温度、湿度的关系
数据集与上题相同,此处不作呈现;
另外采用三种聚类分析方法,包括要求的k-均值聚类、层次聚类,还使用了高斯混合模型(GMM)聚类。
3.1 代码实现
import pandas as pd
import numpy as np
from sklearn.cluster import KMeans, AgglomerativeClustering
from sklearn.mixture import GaussianMixture
import matplotlib.pyplot as plt
plt.rcParams['font.family'] = ['Arial Unicode Ms']
# 读取 Excel 文件并创建数据框
file_path = '实验三3-2.csv'
data = pd.read_excel(file_path)
df = pd.DataFrame(data)
# k-均值聚类
kmeans = KMeans(n_clusters=2)
df['kmeans_cluster'] = kmeans.fit_predict(df[['temperature', 'humidity']])
# 层次聚类
agg = AgglomerativeClustering(n_clusters=2)
df['agg_cluster'] = agg.fit_predict(df[['temperature', 'humidity']])
# 高斯混合模型聚类
gmm = GaussianMixture(n_components=3)
df['gmm_cluster'] = gmm.fit_predict(df[['temperature', 'humidity']])
# 定义红绿蓝颜色列表,熟悉的颜色,可视化效果会更好
colors_rgb = [(1, 0, 0), (0, 1, 0), (0, 0, 1)]
# 可视化结果
plt.figure(figsize=(18, 6))
plt.subplot(131)
plt.scatter(df['temperature'], df['humidity'], c=[colors_rgb[i] for i in df['kmeans_cluster']])
plt.title('K-Means聚类分析结果')
plt.xlabel('温度')
plt.ylabel('湿度')
plt.subplot(132)
plt.scatter(df['temperature'], df['humidity'], c=[colors_rgb[i] for i in df['agg_cluster']])
plt.title('层次聚类分析结果')
plt.xlabel('温度')
plt.ylabel('湿度')
plt.subplot(133)
plt.scatter(df['temperature'], df['humidity'], c=[colors_rgb[i] for i in df['gmm_cluster']])
plt.title('高斯混合模型聚类分析结果')
plt.xlabel('温度')
plt.ylabel('湿度')
plt.show()3.2 聚类分析结果
首先是对每种聚类分析方法中蔟数量的设置,在k-均值聚类方法和层次聚类方法中,蔟设置为2种;高斯混合模型聚类种,蔟设置为3种。
通过观察绘出的图像,可以观察到在高温高湿的条件下形成一类簇,而在低温低湿的条件下形成另一类簇。在低温低湿的条件更为密集,因此低温低湿更适合病毒的生存。
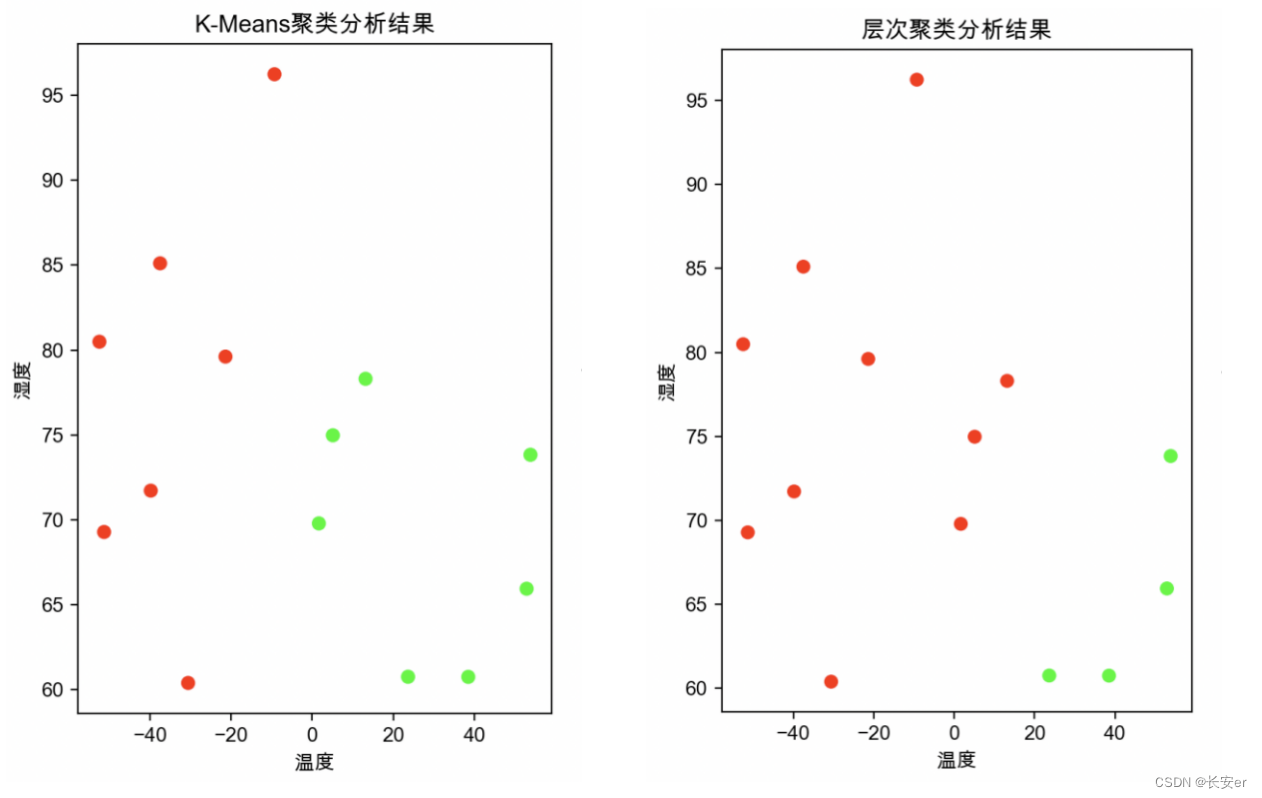
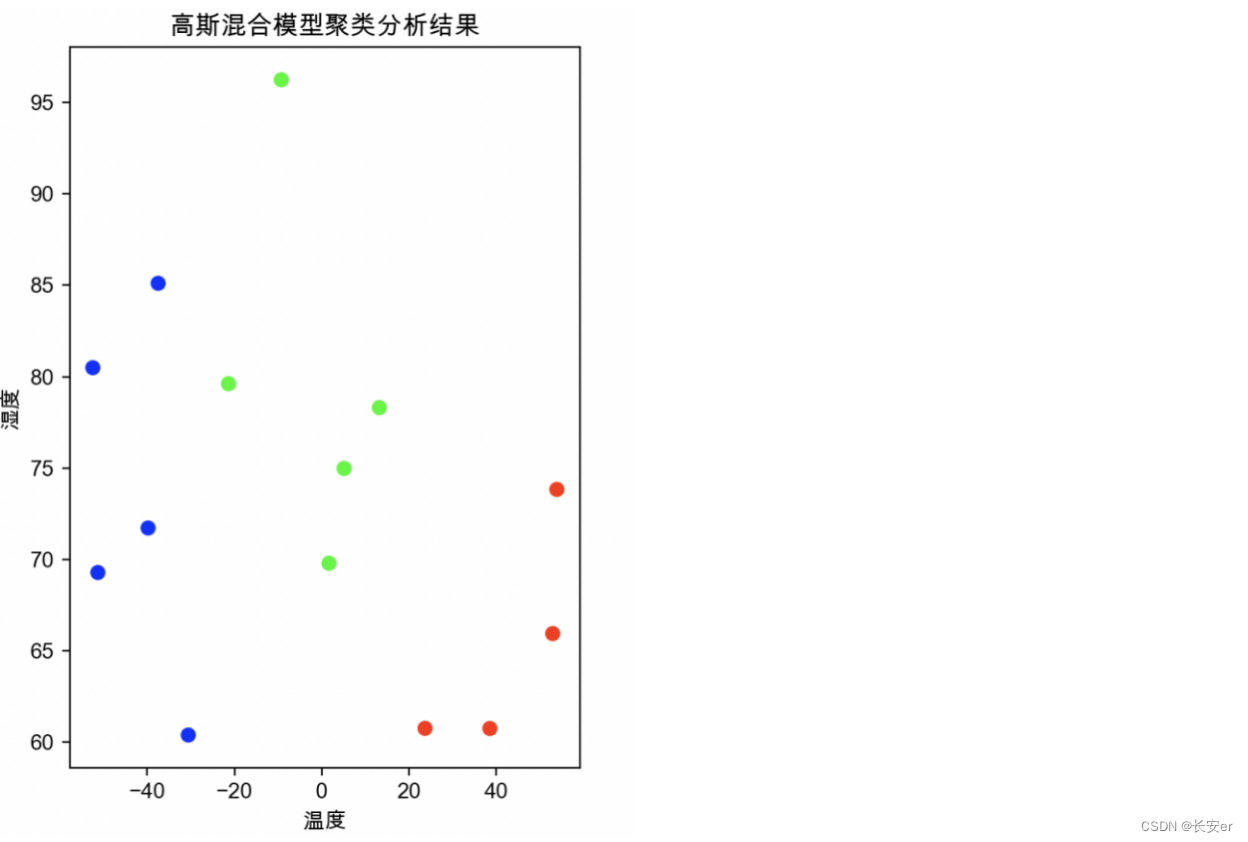
未完待续-----

其实我本以为最终上岸一定是很激动的,但却出奇的平静,但却又那么符合常理。出奇的是自己当初焦虑到做梦都是相关场景,理应非常激动,而不出奇的是与之前打比赛时的经历不谋而合,付出得越多反而越平静。此时的平静自许为成熟的平静,是对于一切结果的坦然,以及聚焦于当下道路的注意力,表现出来的就是当下没有多余的心情让我消费在结果上面,因为我认为人在与环境交互的过程中,总是需要学会接受一切正面和负面的反馈,并且使之不对自己当下的步伐产生负面影响,而这我认为是最大化我们目标的重要学习策略之一。
-------------ypp