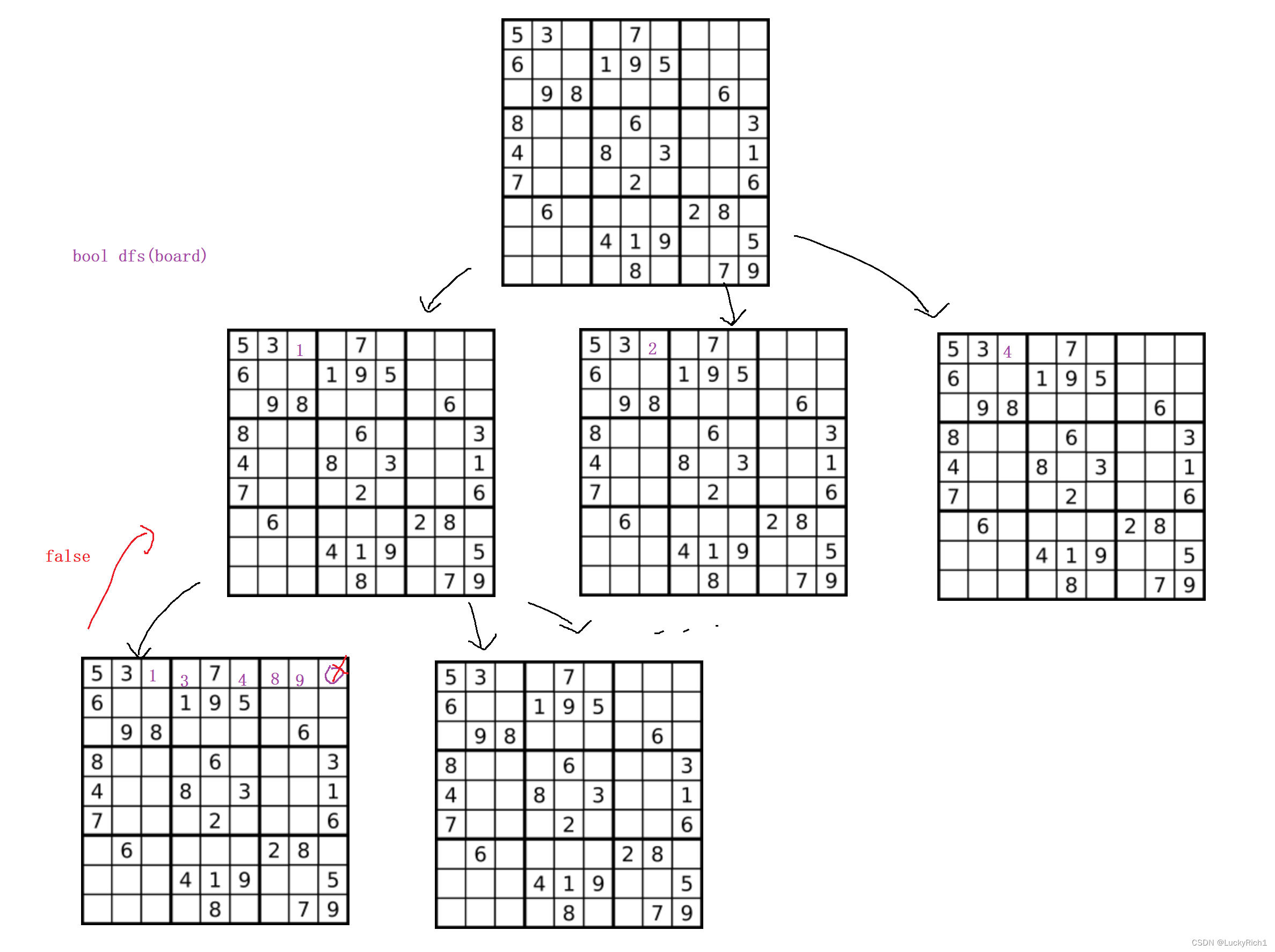
递归、记忆化搜索
【leetcode70 爬楼梯】
class Solution {
public int climbStairs(int n) {
int[] memo = new int[n + 1];
return dfs(n, memo);
}
private int dfs(int i, int[] memo){
if(i <= 1){
return 1;
}
if(memo[i] != 0){
return memo[i];
}
return memo[i] = dfs(i-1,memo) + dfs(i-2,memo);
}
}
上水课的时候在ipad上画的,主要是那老师管的太宽了,大学水课真的太多太烦了。

参考文章 递归、搜索与回溯算法(专题六:记忆化搜索)_记忆化回溯-CSDN博客
斐波那契数

斐波那契数
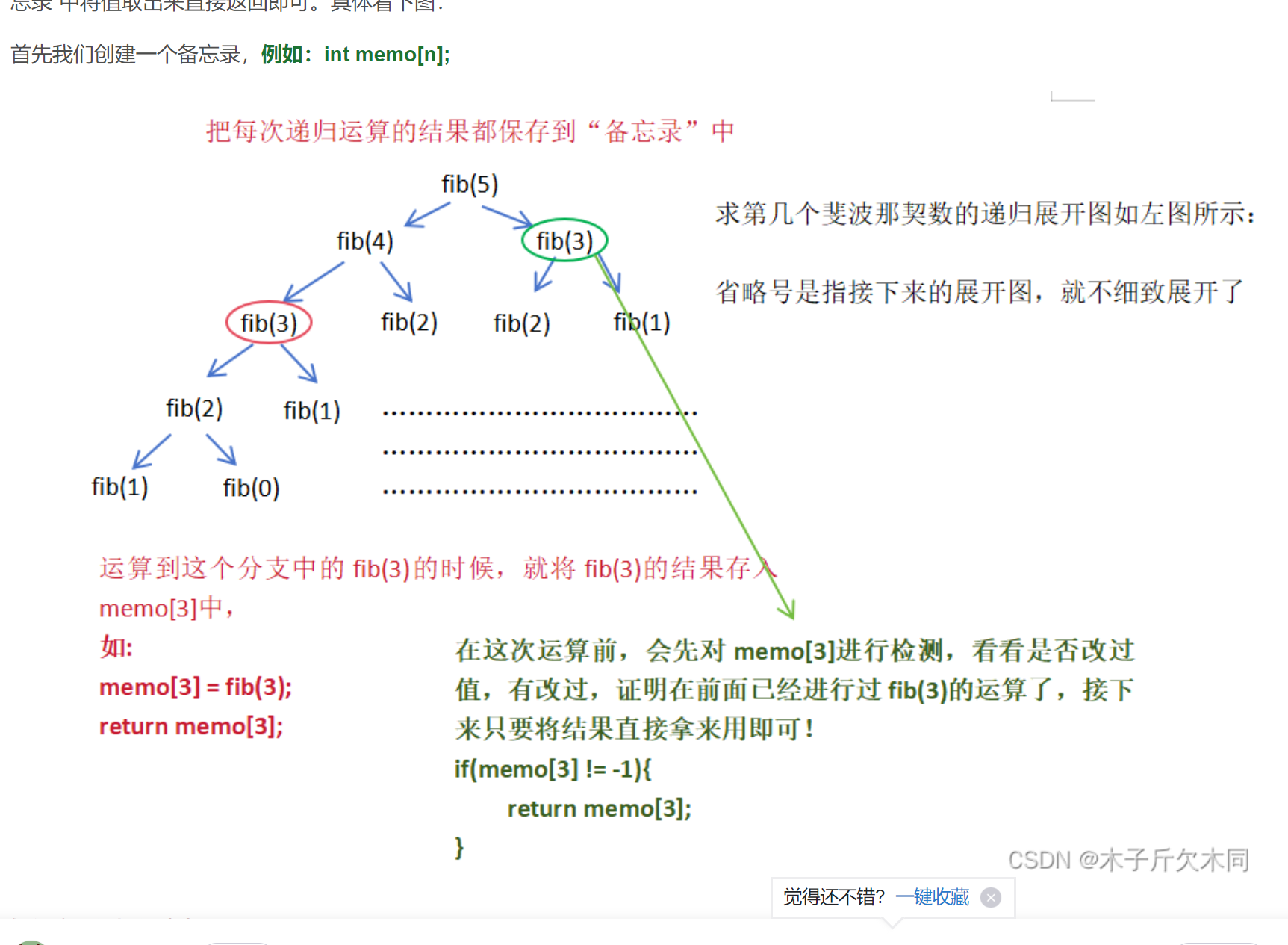
如何实现记忆化搜索?

先复习一下动态规划的核心步骤(5个),并将动态规划的每一步对应记忆化搜索(加强版的递归)的每一步
① 确定动态表示:dp[i]要表示什么,dp[i]表示第i位的斐波那契数 ——> 递归:dfs函数的含义(函数头有什么参数、什么返回值)
② 确定动态转移方程:dp[i] = dp[i - 1] + dp[i - 2] ——> 递归:dfs函数的主体(函数做了什么)
③ 初始化:防止越界,dp[0] = 0,dp[1] = 1 ——> 递归:dfs函数的递归出口(n == 0 或 n == 1时)
④ 确定填表顺序:从左往右 ——> 递归:填写备忘录的顺序
⑤ 确定返回值:dp[n] ——> 递归:主函数如何调用dfs函数
int[] dp;
public void dp(int n) {
dp = new int[n + 1];
dp[0] = 0;
if (n > 0) {
dp[1] = 1;
}
for (int i = 2; i <= n; i++) {
dp[i] = dp[i - 1] + dp[i - 2];
}
}
力扣118. 杨辉三角

class Solution {
public List<List<Integer>> generate(int numRows) {
List<List<Integer>> aa = new ArrayList<List<Integer>>();//泛型
for(int i=0; i<numRows; i++){//行
List<Integer> row = new ArrayList<Integer>();//泛型
for(int j=0; j<=i; j++){//列
if(j == 0 || j == i){//最左边这列和最右边这列都是1
row.add(1);
}else{
row.add(aa.get(i-1).get(j-1) + aa.get(i-1).get(j));
}
}
aa.add(row);
}
return aa;
}
}
又来一题:

class Solution {
public List<Integer> getRow(int rowIndex) {
List<List<Integer>> ret = new ArrayList<List<Integer>>();
// 这里和之前不一样 这里要返回第几行的值 前面要返回前几行的值 所以i <= rowIndex
for (int i = 0; i <= rowIndex; i++) {
List<Integer> row = new ArrayList<Integer>();
for (int j = 0; j <= i; j++) {
if (j == 0 || j == i) {
row.add(1);// 最左边和最右边都是1
} else {
row.add(ret.get(i - 1).get(j - 1) + ret.get(i - 1).get(j));// 一样
}
}
ret.add(row);
}
// 前面return ret;是返回ret数组中的所有
return ret.get(rowIndex);// 返回第几行的值
}
}
好烦,啊啊啊啊啊啊啊啊啊啊啊啊啊向他妈的阳而生。