综合练习三
- 1.优美的排列
- 3.N 皇后
- 3.有效的数独
- 4.解数独

点赞👍👍收藏🌟🌟关注💖💖
你的支持是对我最大的鼓励,我们一起努力吧!😃😃
1.优美的排列
题目链接:526. 优美的排列
题目描述:
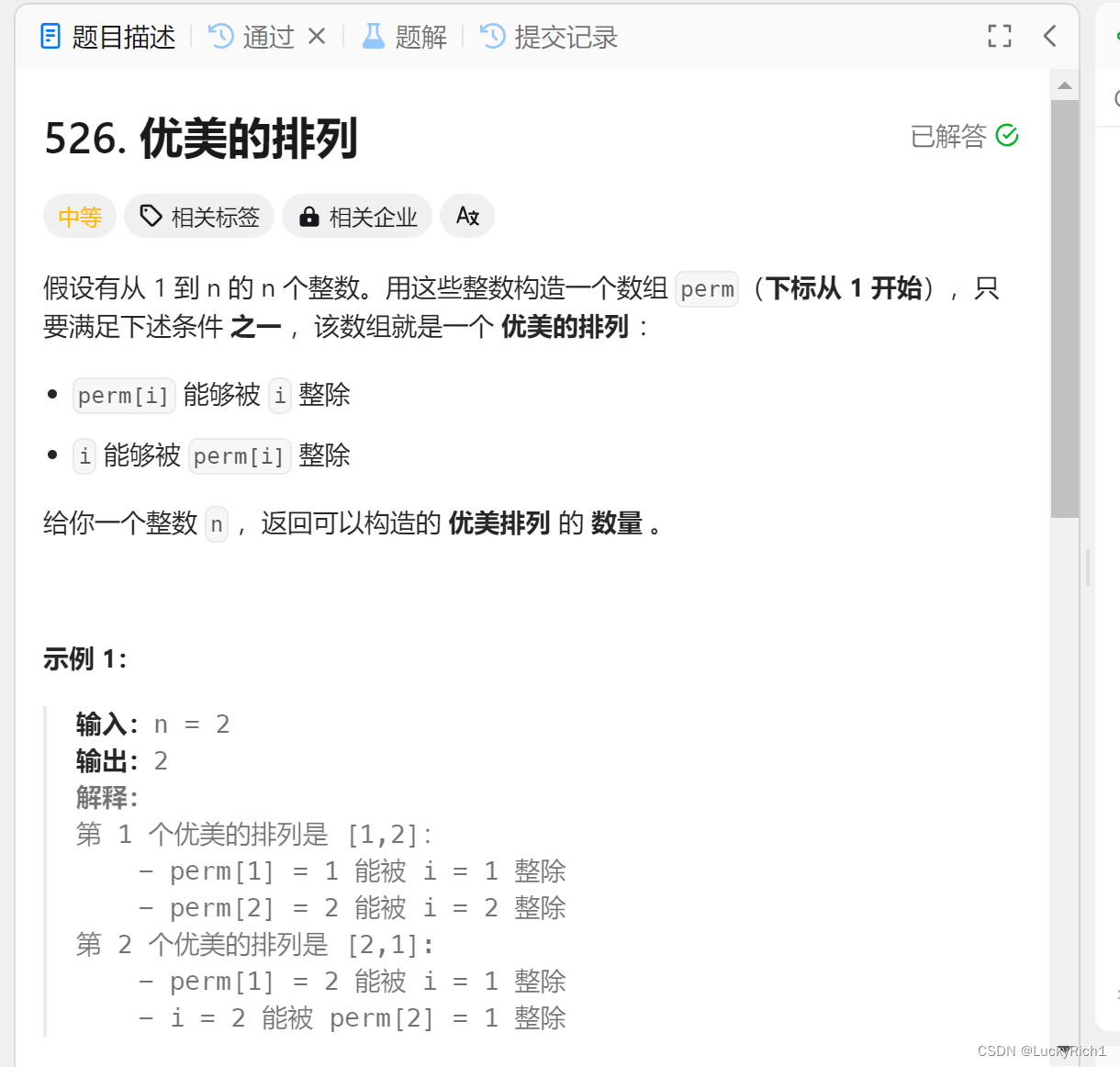
注意一个数字只要能满足 perm[i] 能够被 i 整除 或者 i 能够被 perm[i] 整除,就是优美排列中的数字。
算法原理:
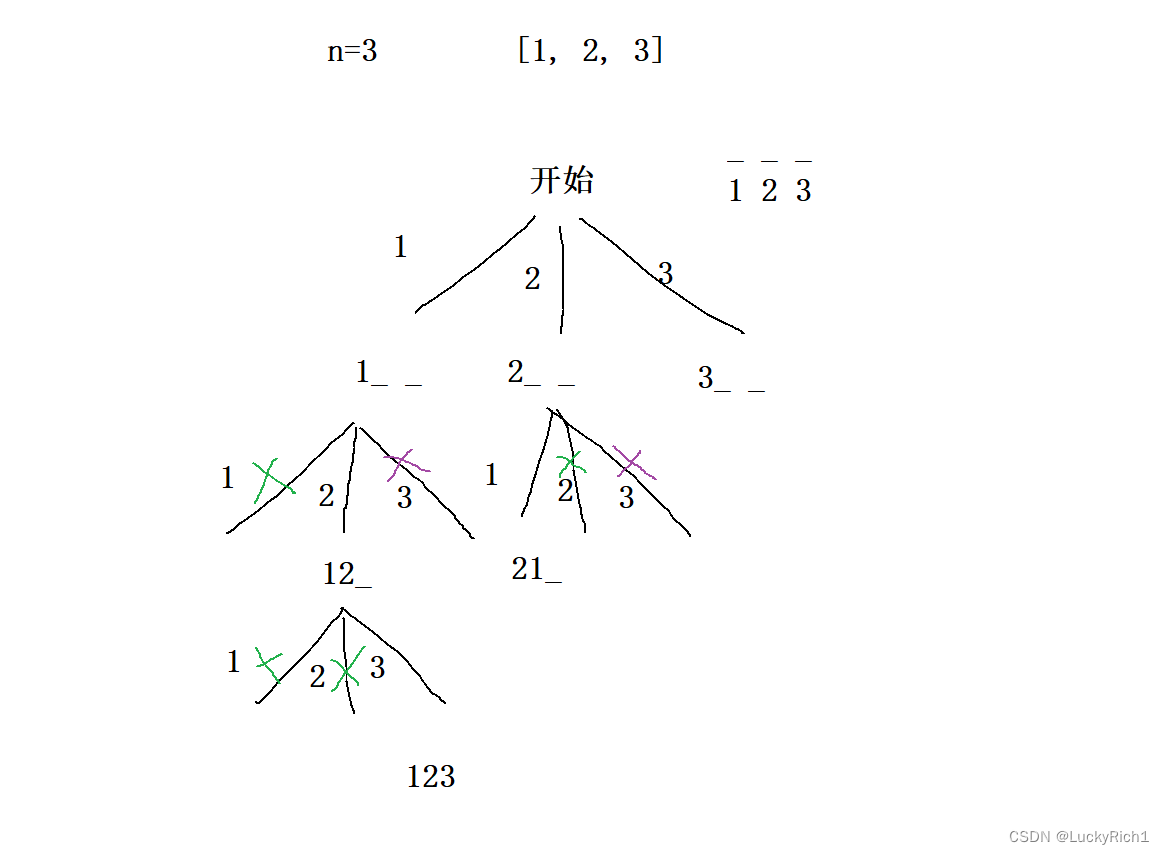
画出决策树,把所有情况不重不漏的找出来。
我们一个位置一个位置的去找,每个位置都有三种选择,但是要注意上一个位置选过的数下一个位置就不要选了。因此可以来一个全局bool 类型数组,记录每个数是否被选过。还有满足 perm[i] 能够被 i 整除 或者 i 能够被 perm[i] 整除 的数才能选。因为这里不需要统计每个组合是什么,我们也不需要path。而只需统计满足情况的有几种就行了。
class Solution {
int ret;
bool check[16];
public:
int countArrangement(int n) {
dfs(n,1);
return ret;
}
void dfs(int n,int pos)
{
if(pos == n+1)
{
++ret;
return;
}
for(int i=1;i<=n;++i)
{
if(check[i] == false && (i%pos == 0 || pos%i == 0))
{
check[i]=true;
dfs(n,pos+1);
check[i]=false; //恢复现场
}
}
}
};
3.N 皇后
题目链接:51. N 皇后
题目分析:
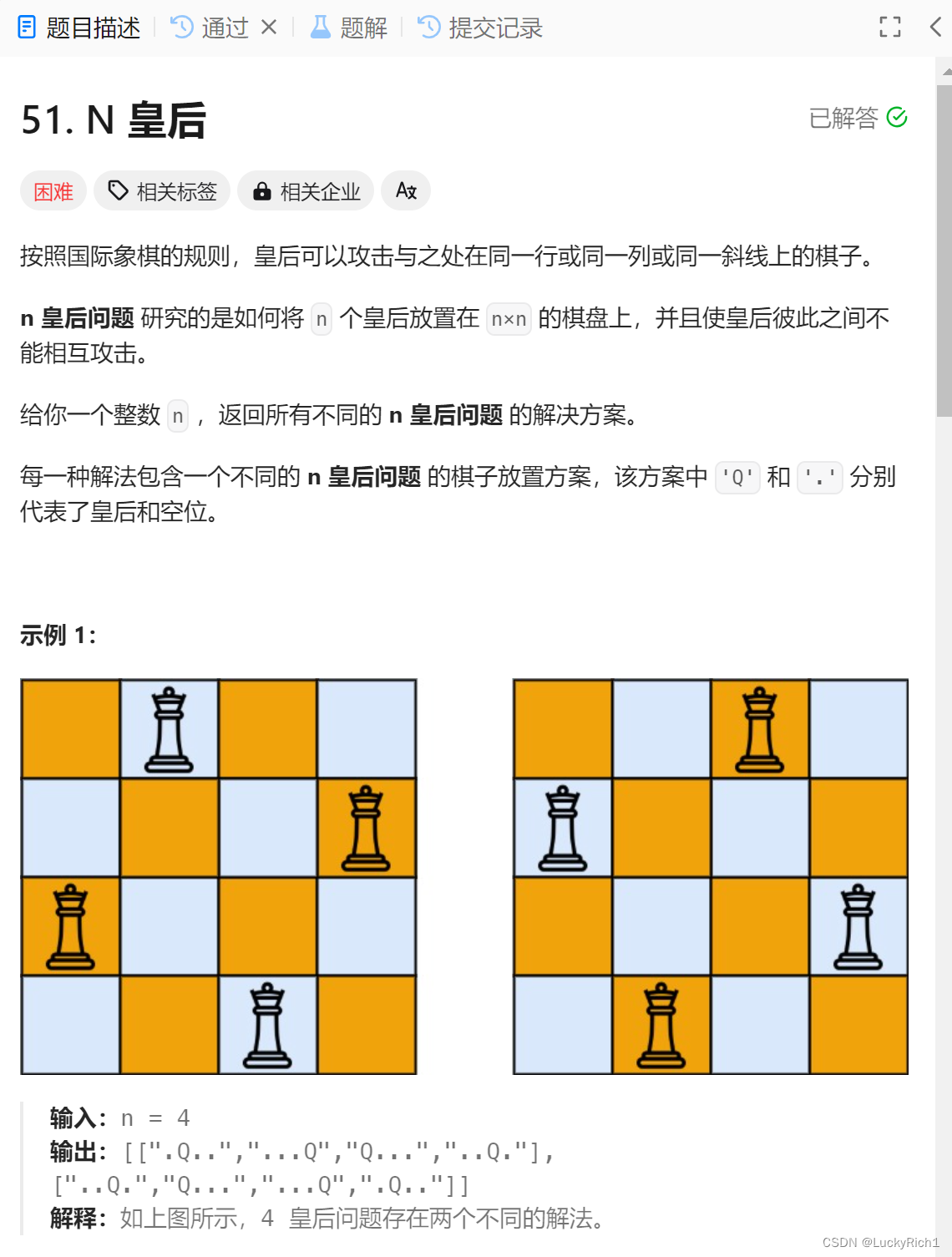
给一个n,代表的是n*n的棋盘,在这个棋盘上放皇后。按照国际象棋的规则,皇后可以攻击与之处在同一行或同一列或同一斜线上的棋子。因此放皇后然后使皇后彼此之间不能相互攻击。问有几种解决方案?
算法原理:
这道题决策树还是比较好看画的,难的是如何剪枝+代码能力!
N皇后的决策树有两种画法,第一种比较麻烦,就是一个小格子一个小格子的来考虑能不能放。第二种就是考虑每次只考虑一行这个皇后应该放哪里。
每行都有n个位置可以放皇后,但是如果放皇后位置满足,皇后在一行或一列或者正对角线或者副对角线的,这个皇后就不能放!全局变量一个ret,一个path,回溯都和前面是一样的。递归函数,就是告诉我一个行数,我就尝试把每一个格子尝试放一个皇后,如果能放就放然后考虑下一行。dfs(row)。递归出口 row==n,说明遇到合法的情况,然后把path放到ret里。我们主要就说剪枝的情况。
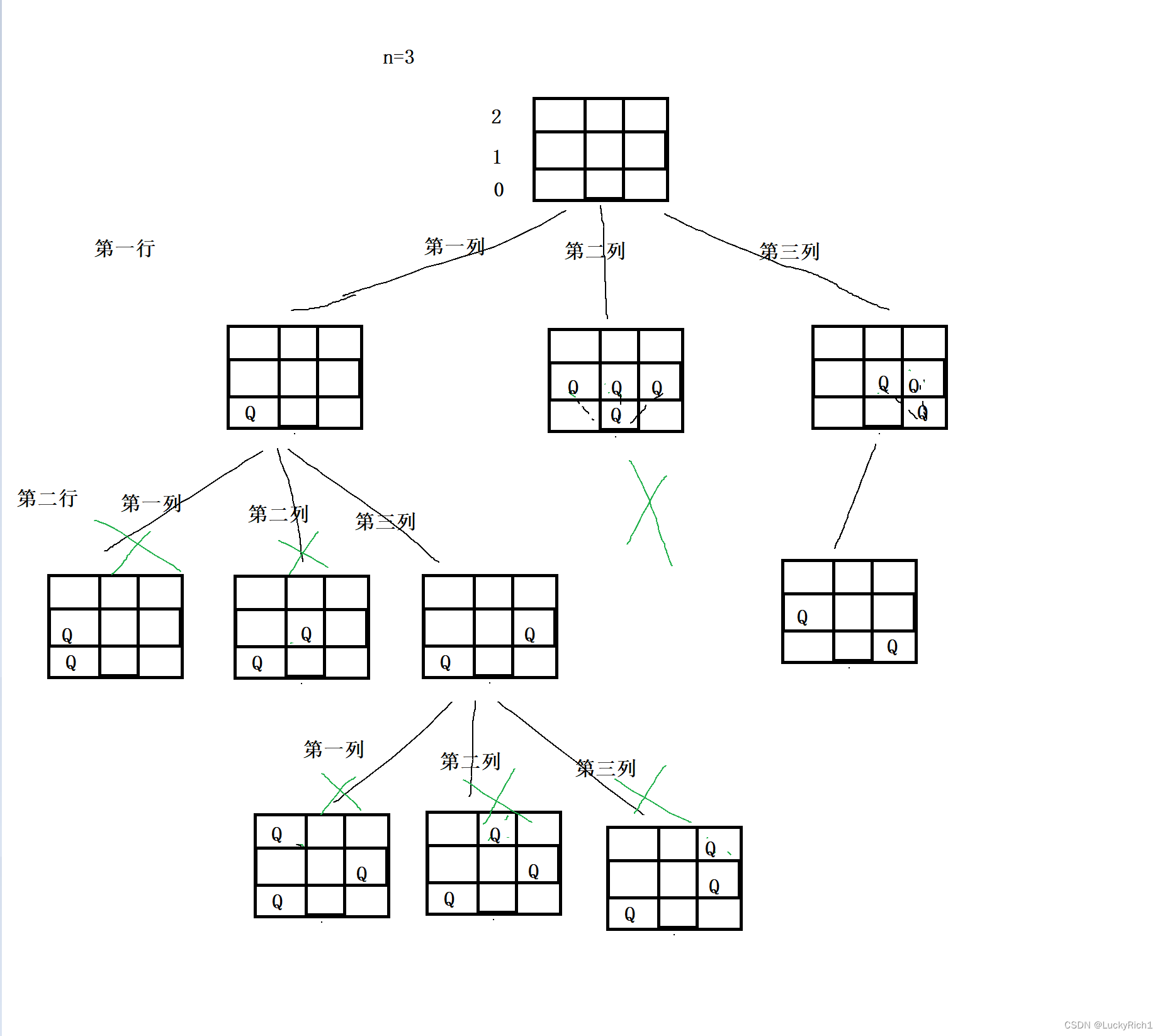
接下来就是剪枝的情况了。
何剪枝:考虑当前这个位置,能否放上皇后?
有两种方法:
1.无脑循环。来四个循环,分别看同一行、同一列、主对角线、右对角线是否有皇后。有这个位置就不能放皇后,都没有就可以放皇后。
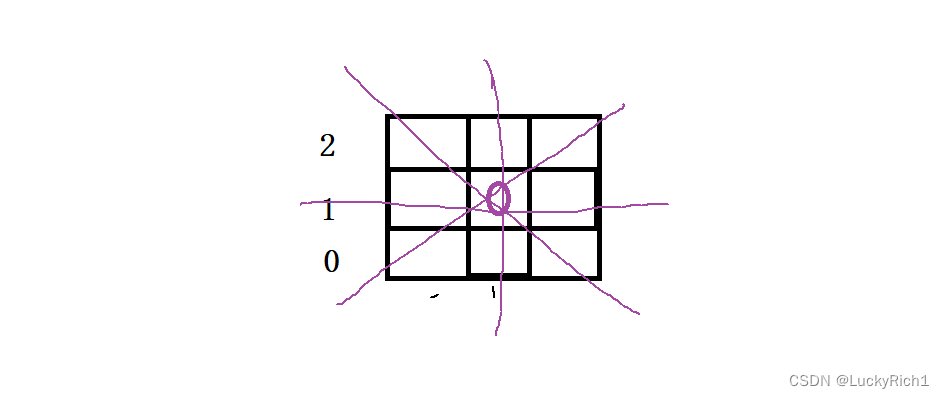
这里我们可以优化一下,没有必要四层循环,三层循环就够了。因为我们都一行一行的枚举,每一行要么第一列放,其他列不放。要么第二列放,其他列不放。要么第三列放,其他列不放。行决定不会出现相互攻击的情况,所有只用看看这一列,主对角线,副对角线有没有。
2.类似哈希表的策略
类似于五子棋那种常用的策略。仅用三个数组就可以搞定!
此时我判断某一列是否有皇后,可以搞一个bool类型大小为n的数组,bool col[n],就可以了。当在0列放一个皇后的时候,可以让col[0]=true, 说明这一列有皇后了。当到其他行的时候第一列就去看col[0]是否等于ture,等于true说明有皇后,不放就可以了。

接下来考虑主对角线和副对角线。我们把这几个位置抽象成几个点放到坐标系里。
主对角线不都是一条斜线吗,主对角线条数=2n-1, 这里是5条,我们就判断这5条对角线就可以了。我们这几条对角线的斜率都是1,因此所有线都可以用 y=x+b表示,此时移位就变成了 y-x=b,这个公式表达的意思是,就看这条红线,它上面的点用纵坐标减去横坐标是一个定值b ,因此继续**搞一个bool类型大小为2n的数组**,当我们发现y-x=b在数组里面是true的话,就说明这个对角线里面有皇后了。因为这个对角线里面y-x全都是一个定值。所以可以把这个定值放到数组下标里面,如果这个位置等于的true,表示这条对角线有皇后了,如果等于false,说明这条对角线没有皇后。
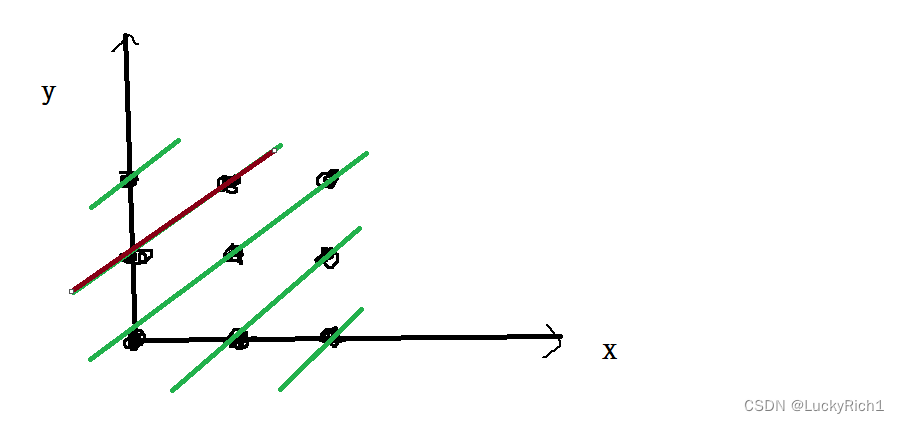
但是这里有一个问题,y-x这里是一个负数,在bool类数组下标里面是不存在负数的,没问题左右两边添加一个偏移量 y-x+n = b+n,通通向上平移n个单位。绝对是一个正数。因此我们求主对角线的时候,就是y-x+n去数组里面看看如果是true,有皇后。如果是false,没有皇后。
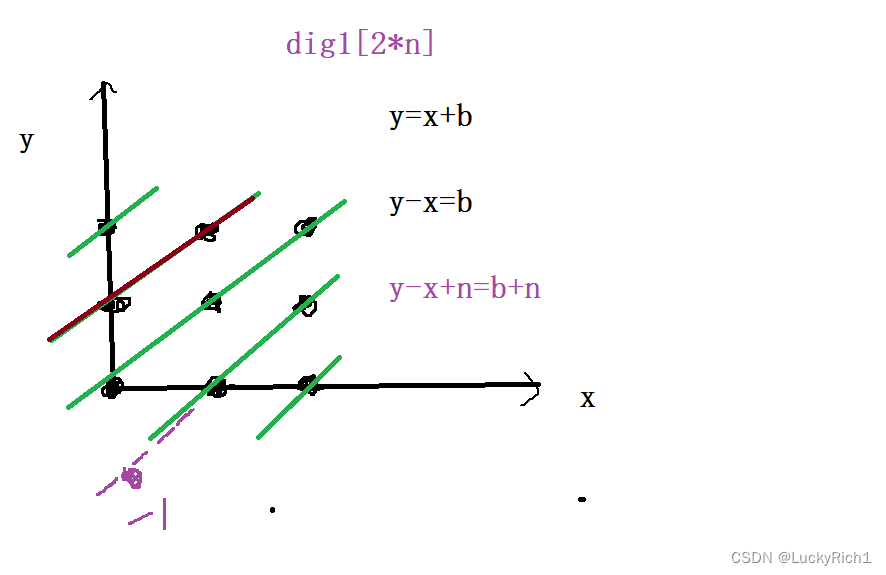
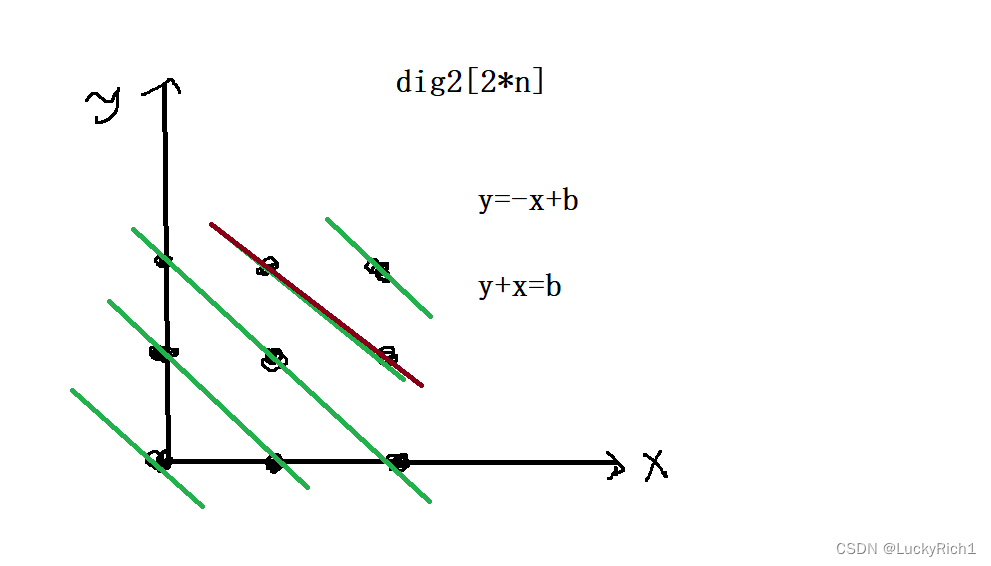
副对角线 斜率为-1, 那就是y=-x+b,此时移位 y+x=b,也就是这单单一条线里面,每一个点横坐标+纵坐标都是一个定值,所以我们又可以搞一个bool类型大小为2*n的数组。当我判断某个位置副对角线里面有没有皇后,我仅需拿这个位置的横纵坐标相加然后去数组找对应位置,如果是true,说明有皇后,如果是false,说明没有皇后。副对角线并不会出现负数的情况。因此只需要判断y+x在dig2是true还是false就行了。
class Solution {
vector<vector<string>> ret;
vector<string> path;
bool checkCol[10],checkDig1[20],checkDig2[20];
int _n;
public:
vector<vector<string>> solveNQueens(int n) {
_n=n;
path.resize(n);
for(int i=0;i<n;++i)
path[i].resize(n,'.');
dfs(0);
return ret;
}
void dfs(int row)
{
if(row == _n)
{
ret.push_back(path);
return;
}
for(int col=0;col<_n;++col)
{
if(!checkCol[col] && !checkDig1[col-row+_n] && !checkDig2[col+row])
{
path[row][col]='Q';
checkCol[col]=checkDig1[col-row+_n]=checkDig2[col+row]=true;
dfs(row+1);
checkCol[col]=checkDig1[col-row+_n]=checkDig2[col+row]=false;
path[row][col]='.';
}
}
}
};
3.有效的数独
题目链接:36. 有效的数独
题目描述:

有效的数独,给一个9x9的格子,把数填满,其中每一行每一列以及3x3宫内,只能填1-9的数字,并且不能重复!
算法原理:
这里的思想和上面N皇后思想是一样的,采用类似哈希映射的方法。你让我判断一行有没有出现重复的元素,我可以搞一个bool类型的二维数组 bool row[9][10],前面9代表0~8行,后面多开一个空间 10个 里面有1~9的数字,row[3][7]=true 说明第三行7已经使用过了。
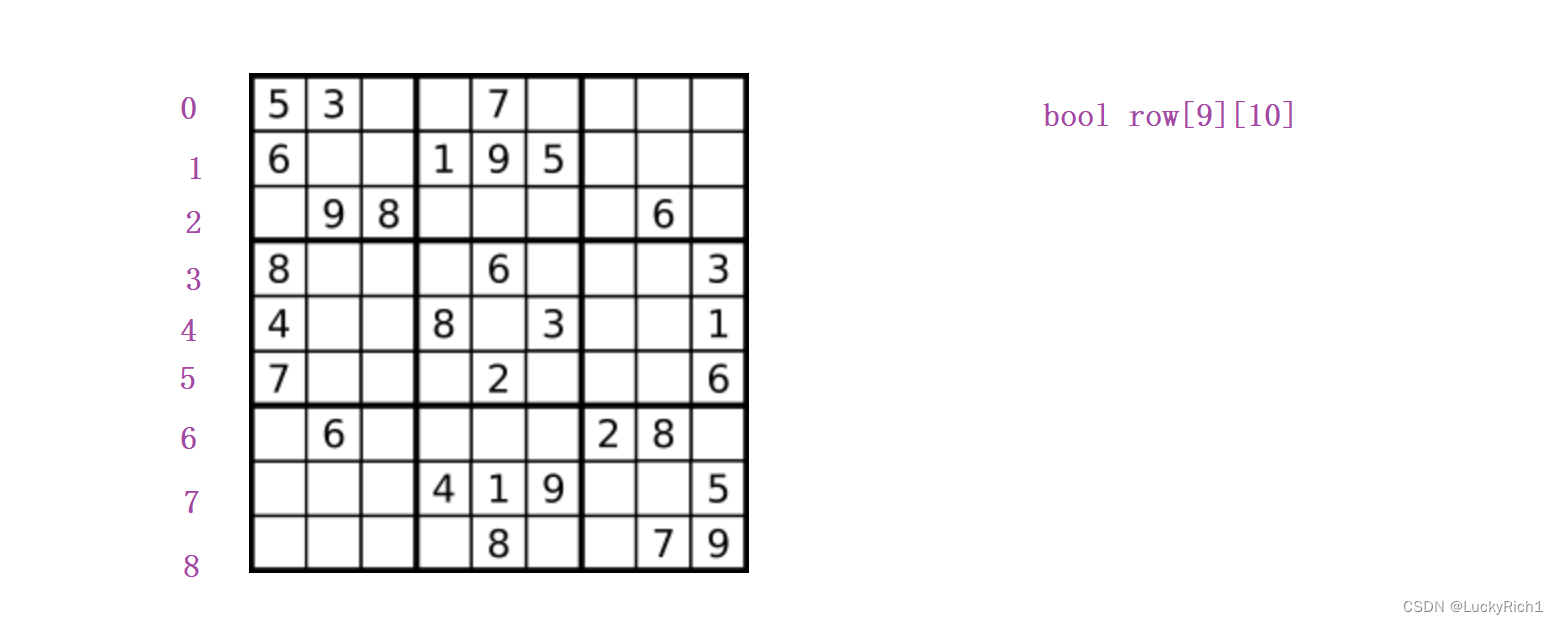
同理,这一列也搞一个bool 类型的二维数组,bool col[9][10],9代表0~8列,10代表有1 ~ 9,col[2][9]=true 代表第2列使用过9这个数字。
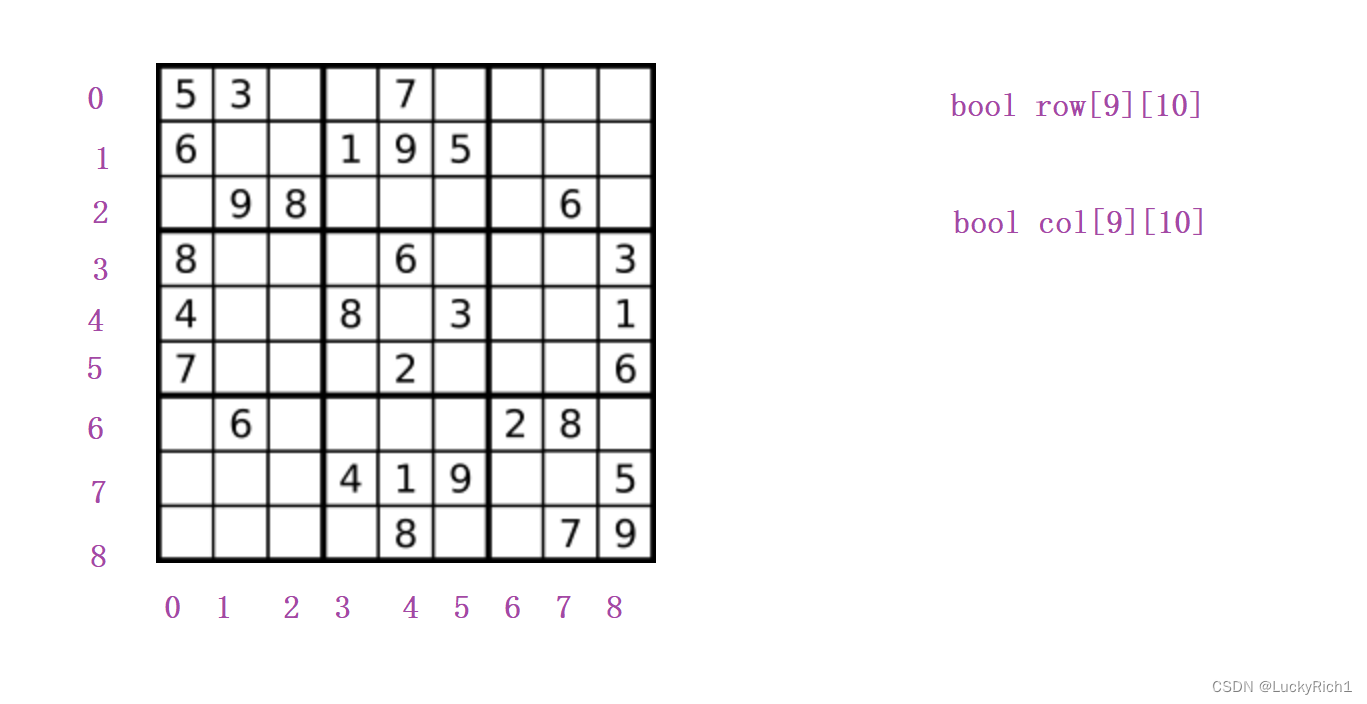
这个3x3的小格子,要么就是横着循环三次,竖着循环三次,但是这样太麻烦了。其实我们也可以搞一个哈希表把它存起来,让3行算作 一行,3列算作 一列。先搞出一个bool类型 bool grid[3][3] ,grid[0][0]代表第一个3x3的格子,grid[0][0]代表第二个3x3的格子,我们用3x3的数组就可以把所有小方格都表示出来了。然后我依旧要看每个3x3格子内数字是否重复,

因此再来一个10,搞成grid[0][0][10]的三维数组,来表示这里9个小方格,这里每个数映射到那个数组也非常好找,用这个数的下标/3,[x/3][y/3]就知道在那个小方格里了,然后10代表这个小方格里的1~9个数数字,grid[0][1][3] =true 表示第2个小放个里面3已经使用使用过了
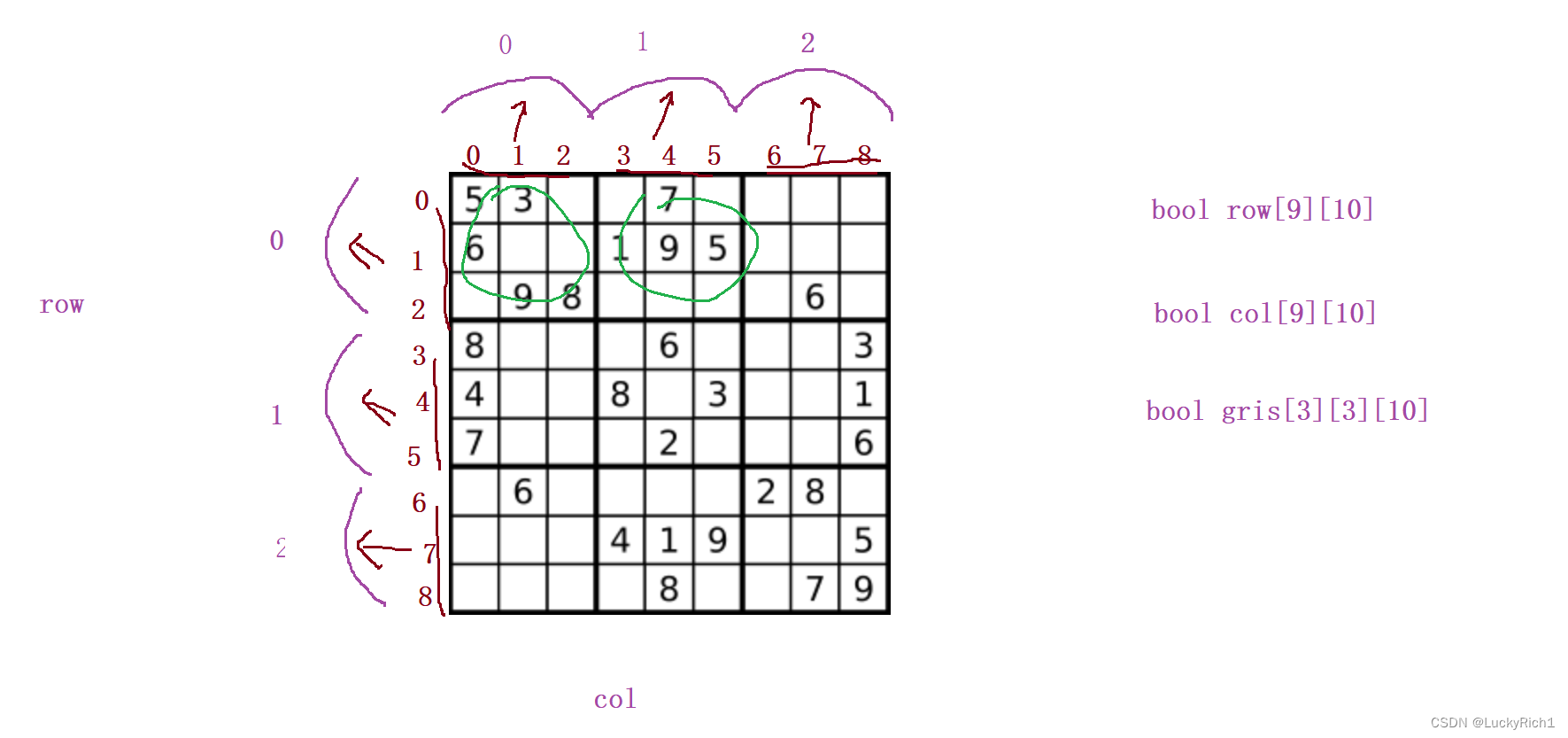
因此我们就可以使用三个bool类型的数组,在O(1)的时间复杂度看一行一列一个小方格有没有出现重复数,这种就是典型的用空间换时间。
class Solution {
bool row[9][10];
bool col[9][10];
bool gids[3][3][10];
public:
bool isValidSudoku(vector<vector<char>>& board) {
for(int i=0;i<9;++i)
{
for(int j=0;j<9;++j)
{
if(board[i][j] != '.')
{
int num=board[i][j]-'0';
if(row[i][num] || col[j][num] || gids[i/3][j/3][num])
return false;
row[i][num]=col[j][num]=gids[i/3][j/3][num]=true;
}
}
}
return true;
}
};
4.解数独
题目链接:37. 解数独
题目描述:

算法原理:
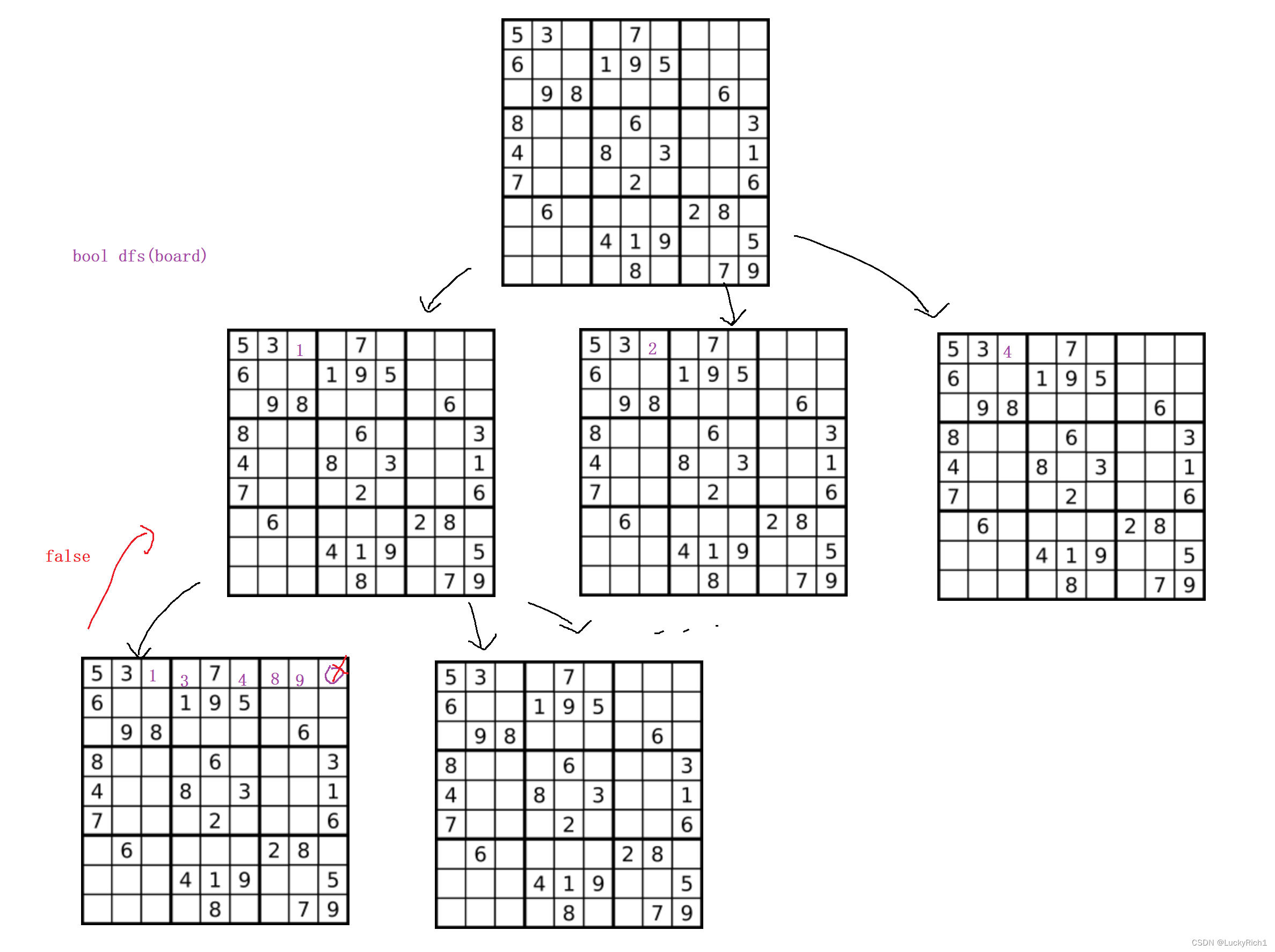
上面的是判断是否是有效数独,这里是填数独。这里还是用上面的三个bool类型数组,来判断这个数能不能放。这里我们一格一格的放,每个格子可以放1-9中其中一个数,但是肯定会是存在剪枝情况的。具体能不能放还是借助那三个bool类型数组来判断。我们递归就是拿着这个棋盘,开始依次遍历,看那个是空的就开始填,填的时候判断一下能填在填不能填就不填。然后能填递归到下一层,但是有可能这个能填的分支下面递归有的位置1 ~ 9都不能填的情况。因此这个分支可能是得不到正确结果的,那上面怎么知道你这种情况不行的呢?因此这个递归函数要有一个bool类型的返回值,当遇到某个格子1 ~ 9都不能填直接向上返回一个false,告诉它这个位置你填1不行,你要把这个位置填上2然后在往下试。递归函数参数只要把这个board给我就行了。bool dfs(board)。
class Solution {
bool row[9][10];
bool col[9][10];
bool grid[3][3][10];
public:
void solveSudoku(vector<vector<char>>& board) {
//初始化
for(int i = 0; i < 9; ++i)
{
for(int j = 0; j < 9; ++j)
{
if(board[i][j] != '.')
{
int num=board[i][j]-'0';
row[i][num]=col[j][num]=grid[i/3][j/3][num]=true;
}
}
}
dfs(board);
}
bool dfs(vector<vector<char>>& board)
{
for(int i = 0; i < 9; ++i)
{
for(int j = 0; j < 9; ++j)
{
if(board[i][j] == '.')
{
//填数
for(int num = 1; num <= 9; ++num)
{
if(!row[i][num] && !col[j][num] && !grid[i/3][j/3][num])
{
board[i][j]='0'+num;
row[i][num]=col[j][num]=grid[i/3][j/3][num]=true;
if(dfs(board) == true) return true; //这个位置填的数已经是最终结果了,不要再往下试了
//恢复现场
board[i][j]='.';
row[i][num]=col[j][num]=grid[i/3][j/3][num]=false;
}
}
return false; //某个位置1~9都不能选,返回false
}
}
}
return true; //已经把数填完了,没有空位置了,返回true
}
};